В восьмой главе рассмотрены общие уравнения строительной механики

ПРЕДИСЛОВИЕ

Предлагаемый вниманию читателей учебник написан в соответ­ствии с программой по строительной механике для студентов строи­тельных специальностей. В связи с появлением ЭВМ строительная механика претерпела серьезные изменения. Поэтому всю историю развития строительной механики можно разделить на два периода: до появления ЭВМ (классическая строительная механика) и после появления ЭВМ. В первой части настоящего курса рассматривается классическая строительная механика. Классические расчетные схе­мы (балки, арки, фермы, рамы, комбинированные системы) позво­ляют понять работу сооружений через работу простейших расчет­ных схем. Это имеет огромное значение для развития инженер­ной интуиции, без которой невозможно проектирование сооруже­ний.

Появление ЭВМ резко расширило рамки строительной механики. Произошел резкий поворот в сторону метода перемещений. Появился метод конечных элементов (МКЭ), позволяющий рассчитывать стер­жневые и нестержневые системы (пластинчатые, оболочечные, пластинчато-стержневые, оболочечно-стержневые и т. д.) с единых позиций. Резко расширились задачи, решаемые в разделе динамики сооружений.

При написании курса авторы стремились, во-первых, максималь­но использовать накопленный опыт преподавания классической строительной механики, во-вторых, отразить современное состояние строительной механики как стержневых, так и нестержневых кон­струкций.

Первые семь глав курса посвящены классической строительной механике. При этом авторы придерживались хорошо методически проработанного традиционного изложения, исключив второстепен­ные вопросы, связанные с упрощением арифметических выкладок (метод упругих грузов, матрицы влияния и т. д.). Дальнейшее из­ложение к^рса является нетрадиционным, поэтому остановимся на этой части подробно.

В восьмой главе рассмотрены общие уравнения строительной механики. Эти уравнения в существующих курсах не нашли долж-

ного отражения, так как их использование приводит к громоздким арифметическим выкладкам при решении практических задач. Однако эти уравнения позволяют более глубоко понять сущность строительной механики. Кроме того, эти уравнения пишутся чисто формально и их составление легко автоматизируется с использова­нием ЭВМ. При этом метод сил и метод перемещений могут рассмат­риваться как способы решения системы уравнений смешанного ме­тода. Далее показана связь уравнений строительной механики с уравнениями теории упругости. Таким образом, показано, что курс строительной механики тесно связан с курсом теории упругости. Общие уравнения строительной механики являются тем мостиком, по которому совершается переход от расчета стержневых систем без использования ЭВМ к расчету стержневых систем с использованием ЭВМ.

В девятой главе рассмотрен расчет стержневых систем с исполь­зованием ЭВМ. Для лучшего понимания расчета на ЭВМ первона­чально рекомендуется провести ряд расчетов на калькуляторах. Широкое использование калькуляторов и их доступность позволяют лучше и быстрее понять работу программы на ЭВМ. Далее показа­но, что наиболее удобным методом расчета стержневых систем на ЭВМ является метод перемещений. В настоящее время все большее распространение получают персональные ЭВМ (например, «Иск-ра-256»). Простота программирования приведет к широкому их использованию как в обучении студентов, так и в практике проекти­рования. В персональных ЭВМ заложен простейший язык БЕЙСИК, в котором имеются операции над матрицами, с использованием ко­торых легко записать алгоритм расчета стержневых систем. Поэто­му курс строительной механики стержневых систем заканчивается описанием простейшего программного комплекса для персональной ЭВМ, который составляется студентами под руководством препода­вателя.

В курсе строительной механики студенты должны составить свой простейший программный комплекс, который они в дальнейшем могут адаптировать для решения тех или иных задач. В спецкурсах или дипломном проектировании студенты должны либо использо­вать свой комплекс, либо применять существующие универсальные программные комплексы (например, ЛИРА, СПРИНТ и др.). При использовании универсальных комплексов центральным вопросом является организация входных и выходных данных, поэтому в на­стоящем курсе рассмотрены эти вопросы с общих позиций.

В десятой главе рассмотрены вопросы расчета стержневых систем с учетом геометрической и физической нелинейности. При изложе­нии расчета стержневых систем с учетом геометрической нелиней­ности рассмотрены также и вопросы устойчивости. Для решения геометрически и физически нелинейных задач предлагается ис­пользовать простейший линейный программный комплекс, состав­ленный студентами по материалам предыдущей главы. При изло­жении расчета стержневых систем с учетом физической нелиней­ности рассмотрены и вопросы приспособляемости.

В одиннадцатой главе изложены основы метода конечных эле­ментов, который является естественным распространением методов расчета стержневых систем на системы нестержневые (континуаль­ные). Общие уравнения стержневых систем, на примере расчета клина, распространяются на решение плоской задачи теории упру­гости и тем самым показывается тесная связь расчета систем стерж­невых с системами нестержневыми. Далее рассматривается МКЭ в форме метода перемещений. Построены матрицы жесткости для прямоугольного и треугольного элементов. Показано, на примере плоской задачи, что при стремлении размеров прямоугольного эле­мента к нулю алгебраические уравнения МКЭ переходят в диффе­ренциальные уравнения теории упругости. Рассмотрены вопросы построения матриц жесткости для сложных элементов, суперэле­ментный подход и особенности комплексов по расчету конструкций с использованием МКЭ.

Следующая, двенадцатая глава посвящена основам динамики. Первоначально рассматриваются системы с одной степенью свободы и подробно изучаются методы решения дифференциального уравне­ния движения. Далее рассматривается система с двумя степенями свободы.

Особенностью изложения раздела динамики является широкое применение численных методов и персональных ЭВМ (значительное количество графиков в этой главе получено с использованием графопостроителя).

При изучении курса предполагается, что читатель знаком с клас­сическим курсом математики в объеме, соответствующем программе вуза, поэтому последняя, тринадцатая глава содержит некоторые дополнительные сведения из математики, используемые в строи­тельной механике. Основное внимание уделено исследованию и ре­шению систем линейных уравнений по методу Гаусса.

Глубокие знания в области строительной механики позволят ин­женеру при проектировании различных конструкций резко снизить их материалоемкость, перейти на производство новых поколений машин, оборудования и крупных экономичных сооружений. Учеб­ник предназначен для студентов вузов строительных специально­стей и может быть использован инженерами-проектировщиками в их практической деятельности. При написании книги широко использован опыт работы на ЭВМ, поэтому учебник полезен также для аспирантов и научных работников, работающих в области строительной механики.

Авторы выражают свою искреннюю благодарность профессорам Н. Н. Леонтьеву и Н. П. Абовскому, а также коллективу кафедры «Строительная механика» Красноярского инженерно-строительного института за сделанные ими замечания, которые способствовали улучшению содержания учебника, а также признательны Л. М. Швацману за составление программ для решения примеров и Л. М. Шапошниковой и И. А. Зубриловой за помощь при оформ­лении рукописи.

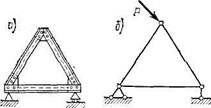
Третьим типом опоры является так называемая защемляющая неподвижная опора, или заделка (рис. 1.5), степень свободы которой равна нулю. Реакция такой опоры определяется тремя параметра­ми, например: величиной и направлением силы, проходящей через произвольную точку, и моментом относительно этой точки. Эту ре­акцию можно представить как сочетание реактивного момента в за­делке (опорном сечении) с реакцией шарнирно-неподвижной опоры.

Схематически опора третьего типа может быть представлена тремя стержнями (рис. 1.6); для того чтобы заделку можно было считать абсолютно жесткой, расстояние 1_й должно быть очень малым или брус на участке длиной /₀ надо рассматривать как бесконечно жесткий.

Отметим, что число стержней в схематическом изображении любой опоры всегда равняется числу параметров, определяющих полную реакцию этой опоры.

§ 1.2. УСЛОВИЯ ГЕОМЕТРИЧЕСКОЙ НЕИЗМЕНЯЕМОСТИ СТЕРЖНЕВЫХ СИСТЕМ Q -^- П V — ^ — - ^х

³ ^ К

,V, 4.,, _ф Ц_

Стержневыми системами называются системы, состоящие из отдельных, обычно прямолинейных, стержней, соединенных между собой в узлах с помощью сварки, заклепок, болтов или других скреп­лений; одним из видов таких систем являются плоские фермы.

В большинстве случаев соединения стержней фермы в узлах являются жесткими — не шарнирными. Точный расчет фермы с та­кими узлами весьма сложен, так как обычно она является много раз статически неопределимой системой. Если жесткие узлы фермы условно заменить шарнирными, то расчет ее значительно упроща­ется и при известных условиях может быть выполнен с помощью од­них лишь уравнений статики. Опытные данные и теоретические исследования показывают, что такая замена допустима, так как при сосредоточенных нагрузках, приложенных в узлах, усилия,

Рис. 1.7

возникающие в шарнирной ферме, мало отличаются от усилий в ферме с жесткими узлами (в случае, когда стерж­ни имеют достаточно боль­шую длину). Поэтому в даль­нейшем будем пользоваться условной расчетной схемой фермы со стержнями, шарнир-, но соединенными в узлах.

Если заменить жесткие узлы системы, состоящей из трех стерж­ней (изображенной на рис. 1.7, а), шарнирами, то система останется геометрически неизменяемой (рис. 1.7, б), т. е. такой, изменение формы которой возможно лишь в связи с деформациями ее элементов. Если же заменить жесткие узлы шарнирами в системе, состоя­щей из четырех стержней (изображенной на рис. 1.8, а), то полу-

чится система геометрически изменяемая (рис. 1.8, б), т. е. такая, форма которой может меняться без деформации ее элементов,

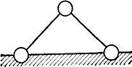
Наипростейшей геометрически неизменяемой, сочлененной из отдельных элементов, шарнирной системой (фермой) является сис­тема, состоящая из трех

стержней, соединенных шарнирами в треугольник (см. рис. 1.7, б).

Установим, как может быть образована геометри­чески неизменяемая систе­ма, состоящая более чем из трех стержней, соеди­ненных шарнирами.

Предварительно рассмотрим систему из двух стержней (рис. 1,9), лежащих на одной прямой и соединяющих узел С с двумя неподвиж­ными точками А и В. Если разъединить стержни АС и ВС в точке С, то конец С стержня АС переместится по окружности т — т, а конец С стержня ВС — по окружности п — п. Эти окружности в точке С имеют общую касательную. Следовательно, если точка С одного из стержней получит весьма малое перемещение по перпен­дикуляру к АВ, то другой стержень не сможет воспрепятствовать

т

S)

■к л		i i i i i	—-9 / / 1
(X J.
	Рис.	1.8

п т

*)

Рис. 1.9

Рис. 1.10

этому перемещению. Таким образом, рассматриваемая система яв­ляется геометрически изменяемой, так как ее форма может меняться при неизменной длине стержней, т. е. при отсутствии деформаций ее элементов.

Систему с двумя стержнями, лежащими на одной прямой (рис. 1.9), в дальнейшем будем называть мгновенно изменяемой, так как она в следующее мгновение после малого смещения точки С по перпендикуляру к прямой АВ превращается в неизменяемую систему.

Иная картина получается, если стержни АС и ВС не лежат на одной прямой (рис. 1.10); в этом случае окружности т — тип — п не имеют общей касательной, а потому даже малое перемещение узла С невозможно без деформации стержней.

Таким образом, всякий новый узел, добавляемый в процессе образования геометрически неизменяемой системы, может быть присоединен с помощью двух стержней, оси которых не должны лежать на одной прямой.

Следовательно, системы, полученные из шарнирного треуголь­ника путем последовательного присоединения узлов, причем каж-

дого двумя стержнями, не лежащими на одной прямой, геометри­чески неизменяемы, т. е. геометрическая структура их неизменяема. Такие системы (или фермы) называют простейшими в отличие от сложных, которые получают обычно в результате видоизменения

в

N

N

/

с 2

простейших, в частности, с по­мощью замены одних стержней дру­гими, или путем наложения одной системы на другую ^х.

11

К простейшим системам отно­сятся фермы, представленные на рис. 1.11. Каждая из них полу­чена последовательным присоедине­нием шарнирных узлов указанным ■ выше способом к основному шар­нирному треугольнику abc в поряд­ке, обозначенном на чертеже циф­рами. В качестве основных тре­угольников abc при проверке гео­метрической неизменяемости прос­тейших ферм могут быть приняты любые шарнирные соединения трех стержней.

Ферма, состоящая только из
треугольников, геометрически не­
изменяема. Любой шарнирный
треугольник ее может рассматри­
ваться как основной. Проверку
геометрической неизменяемости
простейших ферм можно произво­
дить и обратным путем, т. е. по­
следовательно отбрасывая каждый
узел и два стержня, прикрепляю­
щих его к остающейся части фер­
мы. Если в результате этого полу­
чится система в виде шарнирного
треугольника, то рассматриваемая
ферма геометрически неизменяема.
Установим зависимость между
числом узлов и числом стерж-
Рис. 1.11 ней, необходимых для получения

простейшей фермы. Такая ферма,

как уже известно, образуется из основного шарнирного треуголь­ника путем последовательного присоединения новых узлов, при этом каждого с помощью двух стержней, не лежащих на одной прямой.

¹ О структуре плоских систем см. в кн.^- Рабинович И М Кинематический метод в строительной механике. М., Изд. Московского высшего технического училища, 1928,

Обозначим: S — число стержней такой фермы, К — число ее узлов. Основной треугольник имеет три узла и три стержня; каж­дый »з остальных присоединяемых узлов в количестве (К—3) при­крепляется двумя стержнями. Поэтому полное__число стержней в простейшей геометрически неизменяемой ферме ~~~^j

S=3+2(^-3), '

(1.1)

или

S=2K—3.

Рис. 1.12

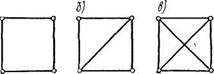Если число стержней S<2K—3, то это показывает, что ферма в своем составе не имеет минимального количества стержней, не­обходимого для образования геометрически неизменяемой ^а) системы. Следовательно, в этом случае система геомет­рически изменяема. Приме­ром такой системы может слу­жить четырехугольник (рис. 1.12, а), в котором 5=4, К= — 4; следовательно,

S=4<2K—3=2-4—3=5.

Превращение его в неизменяемую систему может быть достигнуто
включением пятого диагонального стержня (рис. 1.12, б). Если,
далее, введем вторую диагональ — шестой стержень (рис. 1.12, в),
то с точки зрения геометрической неизменяемости этот стержень
_а) будет уже лишним. Из этого примера видно,

. что могут встречаться геометрически неизме-

няемые системы, в которых S>2K—3.

-5

Рис 1 13

Заметим, что соотношение S^2K—3 явля­ется необходимым, но еще недостаточным ус­ловием неизменяемости фермы. Так, ферма, изображенная на рис. 1.13, а, геометрически изменяема, хотя имеет число стержней S', рав­ное 2/С—3; на рис. 1.13, б изображена изме­няемая ферма, для которой S>2K—3. Из­меняемость этих ферм обьясняется тем, что правые их части представляют собой шарнир­ные четырехугольники. Кроме того, стержневые системы, удовлетворяющие условию S=2K—3, могут быть мгновенно изменяемыми.

Перейдем теперь к вопросу о присоединении геометрически неизменяемой системы к земле посредством опор.

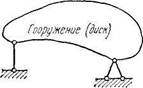
Наиболее часто cooJ)yжgДtШ^(да£iili⁾пиpa_eтcя на две шарнирные опоры, одна из которых неподвижная, другая подвижная (рис. 1.14, а). Такая связь сооружения с землей o6ecne4HBjjeTjyvnr геометрическую неизменяемость^ Не обязательно, чтобы два из трех опорных стержней объединялись одним общим шарниром;

стержни геометрически неизменяемой системы могут и не иметь общих шарниров (рис. 1.14, б).

Если все опорные стержни расположены так, что их направле­ния пересекаются в одной точке О (рис. 1.15, а), то эта точка явля­ется мгновенным центром, вокруг которого система может совер­шать бесконечно малое вращательное перемещение (практически это перемещение может быть конечным, но малым). После такого

а)

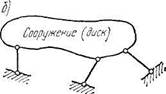
Рис. 1.14

перемещения все опорные стержни уже не будут пересекаться в од­ной точке и потому дальнейшие перемещения будут невозможны без деформации стержней.

Система, прикрепленная к земле подобным образом, обладает мгновенной подвижностью (мгновенной изменяемостью); такое рас­положение стержней недопустимо ¹. Таким образом, прикрепление системы к земле с помощью трех стержней возможно лишь в том

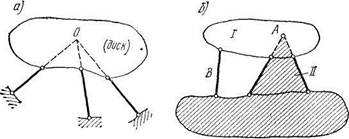
Рис. 1.15

случае, когда оси этих стержней не пересекаются в одной точке и не параллельны друг другу².

Распространяя это положение на случай взаимного соединения двух любых геометрически неизменяемых систем (дисков), можно сформулировать следующее правило: два диска образуют геометри­чески неизменяемую систему, если они связаны между собой с помощью трех стержней, оси которых не пересекаются в одной точке и не параллельны друг другу.

¹ Далее, в § 5.4 показано, что в мгновенно изменяемой системе при действии
даже незначительной внешней нагрузки могут возникать очень большие усилия.

² Так как направления параллельных стержней пересекаются в одной точке,
находящейся в бесконечности,

Если в точке пересечения направлений любых двух из этих трех стержней поставить шарнир и соединить его с диском, то сис­тема не станет геометрически изменяемой, но это даст возможность рассматривать ее как состоящую из двух дисков I и II, связанных друг с другом одним общим шарниром А и стержнем В (рис. 1.15, б). Следовательно, к диску можно геометрически неизменяемо присоеди­нить другой диск с помощью общего для обоих дисков шарнира и стержня, направление которого не должно прохо­дить через этот шарнир.

Ряс. 1.1 в

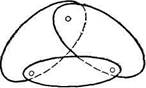
Сочленение трех дисков в одну об­щую геометрически неизменяемую сис­тему можно осуществить, соединив их в ^rj реугольник с помощью трех шарниров, не расположенных на одной прямой (рис. 1.16), или с помощью шести стержней, как это показано на рис. 1.17, так как каждый шарнир может быть заменен двумя стерж­нями, пересекающимися в его центре.

Система, изображенная на рис. 1.18, мгновенно изменяема, так как точки пересечения осей стержней, связывающих каждую пару дисков, лежат на одной прямой. Она аналогична системе, показан­ной на рис. 1.9.

 

 

Рис. 1.17

Рис. 1.18

Итак, три диска, соединенных с помощью шести стержней так, что между каждой парой дисков установлено по два стержня, точки пересечения которых не лежат на одной прямой, представляют со­бой геометрически неизменяемую систему.

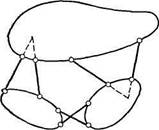
На рис. 1.19, а — к приведен ряд систем, образованных указан­ными способами.

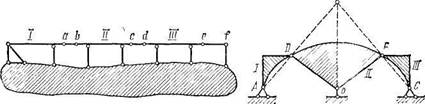
На рис. 1.20 изображена система, представляющая собой один из возможных вариантов многопролетной статически определимой балки (более подробно такого рода системы рассмотрены в § 2.9). Установим ее геометрическую неизменяемость. Для этого выделим из балки какую-нибудь геометрически неизменяемую систему (диск), неподвижно соединенную с землей тремя стержнями, а затем по­стараемся убедиться в том, что каждая следующая геометрически неизменяемая система присоединяется к диску (т. е. к земле и уже присоединенным к ней системам) с помощью трех стержней.

 

Рассматривая стержень /, убеждаемся в том, что он неподвижно соединен с землей тремя стержнями, не пересекающимися в одной точке и не параллельными между собой; стержень //, соединенный двумя стержнями с землей и одним стержнем ab со стержнем /,

4 г)

Рис. 1.19

также образует неизменяемую систему; к этой системе аналогично (с помощью стержня сс/и двух опорных стержней) присоединен стер­жень ///; наконец, к этому стержню посредством шарнира е и опорного стержня присоединен последний элемент ef. Следовательно, вся система в целом является геометрически неизменяемой.

Рис. 1.20

Рис. 1.21

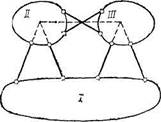
Е

Рассмотрим теперь пример геометрически изменяемой системы (рис. 1.21). Диски / и /// по отношению к диску // можно рас­сматривать как опорные стержни AD и CF; тогда диск // оказыва­ется прикрепленным к земле тремя стержнями AD, CF и верти­кальным стержнем В, оси которых пересекаются в точке Е. Следова­тельно, система является мгновенно изменяемой.

§ 1.3. УСЛОВИЯ СТАТИЧЕСКОЙ ОПРЕДЕЛИМОСТИ ГЕОМЕТРИЧЕСКИ НЕИЗМЕНЯЕМЫХ СТЕРЖНЕВЫХ СИСТЕМ

Выше было установлено, что связь сооружения с землей, схема­тически изображаемая тремя стержнями, не пересекающимися в од­ной точке, геометрически неизменяема. Такая связь статически определима, так как число усилий в этих стержнях равно числу уравнений статики (например, 2^=0, 2^=0 и ^М=0), которые можно составить для плоской системы сил, находящейся в равно­весии.

Сооружение статически определимо относительно опорных за­креплений лишь в том случае, когда число параметров, определяю­щих реакции этих закреплений, равно трем. Этому условию удов­летворяют, например, следующие две системы опорных закреплений:

1) комбинация шарнирно-подвижной и шарнирно-неподвижной
опор — для сооружений, опираю- _а,

щихся в двух точках (рис. 1.22, а);

/

R

2) комбинация трех шарнирно-
подвижных опор (рис. 1.22,6) —
при наличии трех опорных точек в
сооружении; при этом направле­
ния реакций (на рисунке показаны
штриховыми линиями) всех трех
опор не должны пересекаться в од­
ной точке и не должны быть napai-
лельны друг другу.

Рис. 1.22

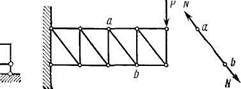
Наличие у геометрически неиз­меняемой системы четырех и более опорных стержней, среди которых имеется три стержня с направле­ниями осей, не пересекающимися в одной точке и не параллельными друг другу, указывает на то, что сооружение статически неопреде­лимо (рис. 1.23). Статически неопределимое сооружение нельзя рас-

~ ^а) - J) ~

Рис. 1.24

Рис. 1.23

считывать с помощью одних лишь уравнений статики; для этого требуется составить дополнительные уравнения,^основанные на изучении его деформаций.

Перейдем теперь к условиям, которым должны удовлетворять сами статически определимые стержневые системы (фермы), т. е. такие системы, усилия в элементах (стержнях) которых могут быть найдены с помощью одних лишь уравнений статики.

При действии на шарнирную ферму сосредоточенных сил, при­ложенных в узлах (шарнирах), в ее прямолинейных стержнях воз­никают одни лишь продольные (сжимающие или растягивающие)

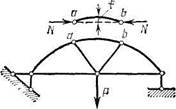
силы. Для доказательства усло­вия этого выделим из фермы (рис. 1.24, а) стержень ab (рис. 1.24, б) и рассмотрим условия его равновесия.

Рис. 1.25

Если к элементу ab непосред­ственно не приложена внешняя на­грузка, то равновесие его возмож­но только тогда, когда силы N, действующие на стержень от шар­ниров а и Ь, равны друг другу по числовому значению величины и направлены в противоположные стороны. Силы N проходят через центры шарниров, так как соеди­нения стержней в узлах предполагаются выполненными с помощью идеальных шарниров (свободных от трения). Следовательно, силы N направлены вдоль прямой, проходящей через центры шарниров а и Ь, а потому вызывают в поперечных сечениях стержня ab лишь продольные силы. Если ферма имеет криволинейные стержни, то в поперечных сечениях этих стержней кроме продольных сил возни­кают изгибающие моменты, вызывающие в них дополнительные на­пряжения. Наибольшие значения этих моментов M=Nf (рис. 1.25).

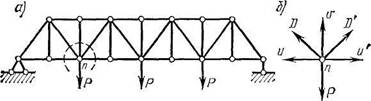
Рис. 1.26

Если ферма в целом (рис. 1.26, а) под действием сил, приложен­ных к ее узлам, находится в равновесии, то и любой из ее узлов (рис. 1.26, б) также находится в равновесии, т. е. внешняя нагрузка, действующая на узел, и внутренние усилия в стержнях, сходящихся в данном узле, взаимно уравновешиваются.

На каждый узел фермы действует система сил, пересекающихся в одной точке. Для такой системы сил статика дает два уравнения равновесия:

2*=о и 2^=о-

Если ферма имеет К узлов, то для них можно составить 2/С урав­нений равновесия, с помощью которых должны быть найдены уси­лия во всех стержнях фермы и три неизвестные опорные реакции.

Дюбые другие уравнения равновесия для отдельных частей фермы (например, группы узлов) или для всей фермы в целом могут быть получены из этих уравнений, а потому не дадут новых условий для определения неизвестных усилий. Следовательно, ферма будет ста­тически определима, если число стержней ее 5 равно удвоенному числу узлов минус 3:

=2^—3.

(1.2)

Полученная зависимость между числом стержней и числом узлов статически определимой фермы совпадает с условием (1.1) ее гео­метрической неизменяемости.

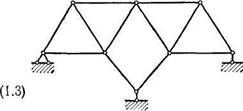Следовательно, всякая простейшая ферма, т. е. ферма, образо­ванная из стержневого шарнирного треугольника последовательным присоединением узлов (каждого с по'мощью двух стержней, не лежа­щих на одной прямой), является системой геометрически неизменяе­мой и одновременно статически определимой.

Если при подсчете числа стержней S системы учесть и опорные стержни, то условие 5=2/С—3 примет вид

Этой формулой удобно пользо­ваться в тех случаях, когда соо­ружение хотя и является геометрически изменяемым (т. е. количество 5 его стержней меньше, чем 2К—3), но так связано с землей, что образует вместе с ней единую геометрически неизменяемую стати­чески определимую систему. Пример такого сооружения дан на рис. 1.27. Для него /С=8, количество стержней в сооружении 5 (без опорных) равно 12. Таким образом, оно не удовлетворяет усло­вию (1.1): S=2K~3 (так как 5=12, а 2/С—3=2-8—3 = 13) и, сле­довательно, является геометрически изменяемым. Однако S_o6ni системы вместе с опорными стержнями, равное 16, удовлетворяет условию (1.3), а потому эта система может быть (и в данном случае является) геометрически неизменяемой статически определимой системой ¹.

Все стержни статически определимой системы являются с точки зрения геометрической неизменяемости безусловно необходимыми, т. е. в такой системе нет ни одной лишней связи (ни одного лишнего стержня).

Если геометрически неизменяемая система в своем составе .имеет
_число стержней, превышающее минимально необходимое, то она
является статически неопределимой. ~ ~

Рис. 1.27

Методы исследования такого рода систем см, в § 4.5,

Глава 1

КИНЕМАТИЧЕСКИЙ АНАЛИЗ СООРУЖЕНИЙ

В курсе строительной механики рассматривается расчет геомет­рически неизменяемых систем (сооружений), т. е. таких, перемеще­ния отдельных точек… Первый тип опоры представлен на рис. 1.1. Он состоит из двух балансиров —…                       …

Рис. 1.1

V////

Рис. 1.3

этому валику верхний балансир может поворачиваться относительно нижнего. Кроме того, он можег (вместе с нижним балансиром, опи­рающимся на катки 4) перемещаться по опорной плоскости, назы­ваемой опорной подушкой 5.

Рассматриваемая опора имеет, следовательно, две степени сво­боды (изменяемости). Трением, развивающимся в опоре, принято при расчете пренебрегать, а потому реакция такой опоры представ-

¹ Под термином «земля» понимается геометрически неизменяемая система —
диск

² В дальнейшем при расчете плоских систем цилиндрический шарнир будем
называть шарниром.

ляет собой силу, проходящую через центр шарнира и перпендику­лярную направлению возможного перемещения катков, т. е. верх­ней плоскости опорной подушки. Эта сила определяется одним па­раметром —'- ее величиной. Рассматриваемая опора носит название цилиндрической подвижной или шарнирно-подвижнои. Схематически ее изображают в виде одного стержня с двумя идеальными (без трения) шарнирами на концах¹ (рис. 1.2).

У/////////.

V/,

Рис. 1.4

Рис. 1.5

Стержень, схематически изображающий шарнирно-подвижную опору, условно принимается бесконечно длинным; верхняя точка такого стержня может перемещаться лишь по прямой линии (прямая есть окружность бесконечно большого радиуса), перпендикулярной его оси, что полностью соответствует тем условиям, в которых на­ходится действительная шарнирно-подвижная опора. Собственные деформации опоры при расчетах не учитываются, т. е. опорный стержень условно считается бесконечно жестким.

У////////////////////////А

Опорное сечение

I Рис. 1.6

Второй тип опоры (рис. 1.3) отличается от первого тем, что ниж­ний балансир 3 закреплен и не может перемещаться. Такая опора обладает одной степенью свободы и носит название цилиндрической неподвижной или шарнирно-неподвижной. Реакция ее представляет собой силу, проходящую через центр шарнира. Эта сила может иметь любое направление и опре­деляется, следовательно, двумя параметрами — величиной и на­правлением (или, что то же са­мое, величинами двух состав­ляющих ее сил, например вер­тикальной и горизонтальной).

Схематически опора второго

типа изображается с помощью двух стержней с идеальными шарнирами по концам; верхний шарнир является общим для обоих стержней (рис. 1.4). Такая схема опре­деляет точку приложения опорной реакции (центр верхнего шарни­ра), оставляя ее направление неизвестным.

Направления стержней на схеме шарнирно-неподвижной опоры могут быть выбраны вполне произвольно, так как силу (реакцию) можно разложить на два любых направления.

¹ Иногда шарнирно-подвижная опора осуществляется в виде колонны с дву­мя шарнирами по концам, тогда она называется качающейся опорой или качаю­щейся стойкой,