рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Механика
- /
- КОЛЕБАНИЯ, ВОЛНЫ, ЗВУК
Реферат Курсовая Конспект
КОЛЕБАНИЯ, ВОЛНЫ, ЗВУК
КОЛЕБАНИЯ, ВОЛНЫ, ЗВУК - раздел Механика, Колебания, Волны, Звук ...
КОЛЕБАНИЯ, ВОЛНЫ, ЗВУК
Любые отклонения физического тела или параметра его состояния, то в одну, то в другую сторону от положения равновесия называется колебательным движением или просто колебанием.
Колебательное движение называется периодическим, если значения физических величин, изменяющихся в процессе колебаний, повторяются через равные промежутки времени.
Несмотря на большое разнообразие колебательных процессов, как по физической природе, так и по степени сложности, все они совершаются по некоторым общим закономерностям и могут быть сведены к совокупности простейших периодических колебаний, называемых гармоническими.
Гармоническими называются колебания, совершающиеся по законуsin или cos.
s = Asin (ωt +φ0), s = Acos (ωt +φ0)
Они совершаются под действием квазиупругих сил, т.е. сил, пропорциональных смещению
F = -kx
Основными характеристиками колебаний являются:
1. Смещение (s) — это расстояние, на которое отклоняется колеблющаяся система в данный момент времени, от положения равновесия.
2. Амплитуда (А) — максимальное смещение.
3. Период (Т) — время одного полного колебания.
Линейная частота (v) — это число колебаний в единицу времени, измеряется в Гц - это одно колебание в сек. v = 1/Т.
5. Циклическая или круговая частота (ω). Она связана с линейной частотой следующей зависимостью: ω= 2πv.
6. Фаза колебания (φ) характеризует состояние колеблющейся системы в любой момент времени: φ = ωt + φ0, φ0- начальная фаза колебания.
Колебательный процесс можно представить графически в виде развернутой или векторной диаграммы.
Развернутая диаграмма представляет собой график синусоиды или косинусоиды, по которому можно определить смещение колеблющейся системы в любой момент времени.
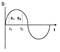

Способ представления колебаний с помощью вращающегося вектора амплитуды называется векторной диаграммой. Проведем "опорную" ось ОХ, и построим вектор А, численно равный амплитуде колебания, направленный из точки О под углом φ0 к опорной оси, равным начальной фазе. So выражает смещение в начальный момент времени t = 0 (1). Будем вращать вектор вокруг оси О, перпендикулярной к плоскости чертежа, с угловой скоростью со против часовой стрелки. За промежуток времени t вектор амплитуды повернется на угол φ = ωt (2), а его проекция на опорную линию определится как s = Acos (ωt + φ0). За время равное периоду колебаний вектор повернется на угол 2π, а проекция его конца совершит одно полное колебание около положения равновесия О. Следовательно, вращающийся вектор амплитуды полностью характеризует колебательное движение в любой момент времени. Большинство колебательных процессов в биологии и медицине являются не гармоническими, а сложными. Однако, любое сложное колебание можно представить в виде суммы гармонических. Это положение определяет специальный метод диагностики -спектральный анализ.
Совокупность гармонических составляющих, на которые разлагается сложное колебание, называется гармоническим спектром этого колебания.
Колебания распределяются на следующие основные виды: 1. Свободные - это идеальные колебания, которые не существуют в природе, но… 2. Затухающие - это колебания, амплитуда которых со временем уменьшается, а частота не меняется и близка к…S = Asin ωt
Полная энергия складывается из потенциальной и кинетической энергии:
W=Wn+Wk
Wn=ks2/2=(kA2/2)sin2ωt, где k=mω
W=mυ2/2, учитывая, что υ=ds/dt=Aωcosωt
Получим Wk=(mω2A2/2)*cos2ωt
Тогда полная энергия:
W=(mω2A2/2)(sin2ωt+cos2ωt)=(mω2A2)/2
Таким образом, полная энергия колеблющегося тела прямо пропорциональна массе, квадрату амплитуды, квадрату циклической частоты и не зависит от времени. Возникновение колебаний в какой-либо точке пространства не является локальным процессом. Они передаются другим участкам, если между ними имеется механическая, электрическая или другая связь.
Процесс распространения колебаний в пространстве называется волновым движением или просто волной.
Известны два вида волн: механические и электромагнитные. Механические волны распространяются только в упругих средах. Механические волны делятся на два вида: поперечные и продольные.
Если колебания частиц совершаются перпендикулярно направлению распространения волны, то она называется поперечной.
Рассмотрим, основные характеристики волнового движения. К ним относятся: 1. Все параметры колебательного процесса (s, A, v, ω, Т, φ). 2. Дополнительные параметры, характеризующие только волновое движение:Величина, численно равная среднему значению энергии, переносимой волной в единицу времени через некоторую поверхность, перпендикулярную направлению распространения волны, называется потоком энергии через эту поверхность.
Ps=W0/t (Вт)
Поток энергии, приходящийся на единицу поверхности, называется плотностью потока энергии или интенсивностью волны.
J=Ps/s = W0/st (Вт)
Частным случаем механических волн являются звуковые волны:
Звуковыми волнами называются колебания частиц, распространяющихся в упругих средах в виде продольных волн с частотой от 16 до 20000 Гц.
1. Интенсивность звуковой волны называют силой звука.J=Ps/s (Вт/м2) Для этой величины приняты специальные единицы измерения- Белы (Б) и децибелы… где Jo = 10-12 Вт/м2 - некоторая пороговая интенсивность.Звуковым или акустическим давлением называется добавочное давление (избыточное над средним давлением окружающей среды) в местах наибольшего сгущения частиц в звуковой волне.
В системе СИ оно измеряется в Па, а внесистемной единицей является 1 акустический бар = 10-1Па.
3. Важное значение имеет так же форма колебаний частиц в звуковой волне, которая определяется гармоническим спектром звуковых колебаний (∆v).
Все перечисленные физические характеристики звука называются объективными, т.е. не зависящими от нашего восприятия. Они определяются с помощью физических приборов. Наш слуховой аппарат способен дифференцировать (различать) звуки по высоте тона, тембру и громкости. Эти характеристики слухового ощущения называются субъективными. Изменение в восприятии звука на слух всегда связано с изменением физических параметров звуковой волны.
Высота тона определяется главным образом частотой колебаний в звуковой волне и незначительно зависит от силы звука. Чем больше частота, тем выше тон звука. В этом отношении диапазон звуков, воспринимаемых слуховым аппаратом, делится на октавы: 1- (16-32) Гц; 2 -(32-64)Гц; 3-(64-128) Гц; и т.д., всего 10 октав.
Если колебания частиц в звуковой волне гармонические, то такой тон звука называется простым или чистым. Такие звуки дают камертон и звуковой генератор.
Если колебания не гармонические, но периодические, то такой тон звука называется сложным. .
Если сложные звуковые колебания не периодически меняют свою интенсивность, частоту и фазу, то такой звук принято называть шумом.
Громкость восприятия звука зависит главным образом от силы звука, а так же от частоты. Эта зависимость определяется психофизическим законом…При возрастании силы звука в геометрической прогрессии (J,J2, J3,...) ощущение громкости на одной и той же частоте увеличивается в арифметической прогрессии (Е, 2Е, ЗЕ,...).
E=kLg J/J0
где k - коэффициент, зависящий от частоты звука. Громкость измеряется также как и сила звука в Белах (Б) и децибелах (дцБ). ДцБ громкости называется фоном (Ф) в отличии от дцБ силы звука. Условно считают, что для частоты 1000 Гц, шкалы громкости и силы звука полностью совпадают, т.е. k = 1. Громкость на других частотах можно измерить, сравнивая исследуемый звук с громкостью звука на частоте 1000 Гц. Для этого пользуются кривыми равной громкости, построенными на основании средних данных, которые были получены у людей с нормальным слухом при измерениях, проводимых этим методом.
Использование звуковых методов в диагностике
а) Исследование органов слуха с помощью аудиометра-генератора, в котором плавно или дискретно меняются частота и интенсивность звука. По данным… б) Исследование слуха с помощью камертонов. в) Исследование этими методами по воздушной и костной проводимости.Ультразвук - это процесс распространения, колебаний в уп-пугой среде в виде продольных волн с частотой свыше 20 кГц.
Ультразвук получают с помощью специальных аппаратов, основанных на явлениях магнитострикции - при низких частотах и обрат-ном пьезоэлектрическом эффекте - при высоких частотах.
Магнитострикция - это изменение продольных размеров ферромагнитного стержня при воздействии на него высокочастотным (20—100 кГц) магнитным полем.
Обратный пьезоэлектрический эффект заключается в изменении размеров пьезодиэлектрика под воздействием на него высокочастотным (свыше 100 кГц)…Свойства ультразвуковых волн
2. Скорость распространения ультразвука зависит как от среды, в которой он распространяется, так и от состояния этой среды (температуры, давления,… 3. Ультразвук активно отражается от границы раздела сред с разным… 4. Ультразвуковая волна обладает достаточно большой энергией, которая зависит от частоты, поэтому при распространении…ФИЗИЧЕСКИЕ ОСНОВЫ ГЕМОДИНАМИКИ
Гидродинамика — это раздел физики, изучающий законы движения и силы взаимодействия в жидкостях.
Механические свойства жидкости обусловлены силами, действующими между молекулами. Рассмотрим стационарное течение идеальной жидкости по трубе переменного сечения.
Течение жидкости называется стационарным или установившимся, если с течением времени скорость частиц жидкости в каждой точке потока не изменяется.
Идеальной называется жидкость, не обладающая внутренним трением и несжимаемая. К такой жидкости по своим свойствам близок гелий при сверхнизких температурах. Для идеальной жидкости при стационарном течении скорости течения обратно пропорциональны площадям поперечного сечения.
S1/S2 υS=const
Это уравнение неразрывности струи. Уравнение Бернулли и его следствие.
Для идеальной жидкости, при установившемся течении сумма трех энергий (потенциальной энергии сил давления, потенциальной энергии сил тяжести и кинетической энергии) для любого сечения есть величина постоянная.

P1V + mgh1 + (mυ12)/2 = P2V = mgh2 + (mυ22)/2
PV + mgh + (mυ2)/2 =const
Уравнение Бернулли может быть выражено и в другом виде. Поделим все члены уравнения на V.
PV)/V + (mgh)/V + (mυ2)/2V = const
P + pgh + (pυ2)/2 = const
При стационарном течении идеальной жидкости сумма трех давлений есть величина постоянная в любом поперечном сечении потока.
Р - называется статическим давлением; pgh - гидростатическим давлением; pυ2 /2 - динамическим давлением. Рассмотрим физическую сущность этих видов давлений в жидкости.
Статическое или истинное давление - это давление, с которым один слой жидкости давит на другой. Статическое давление может создаваться различными внешними причинами (за счёт работы насоса, за счёт потенциальной энергии воды в водонапорной башне и т.д.).
Гидростатическое давление обусловлено весовым давлением вышележащего слоя (столба) жидкости на нижележащий.
Динамическое давление - это давление, создаваемое движущейся жидкостью. Оно проявляется при торможении жидкости и обусловлено кинетической энергией частиц жидкости.
Измеряется статическое давление при помощи прямой манометрической трубки, плоскость отверстия которой расположена параллельно движению жидкости. Полное давление измеряется манометрической
трубкой, изогнутой под прямым углом навстречу движению жидкости. Это давление является суммой статического и динамического давлений.
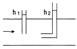
Динамическое давление определяют по разности между полным и измеренным одновременно статическим давлением. Рдин= Рn - Рст В нашем примере Рдин= h2 - h1
Единицы измерения давления: СИ - Н/м2 [Па], СГС - дн/см2, 1Па = 10 дн/см2.
Внесистемные единицы давления: техническая атмосфера (ат), 1ат = к Гс/см2 = 9,8 104Па,
физическая атмосфера (атм), 1атм = 760 мм.рт.ст. = 1,013 105 Па, 1мм.рт.ст. = 13.6 мм.вод.ст.
В метеорологии применяется единица давления, называемая баром, 1 бар = 105 Па = 750 мм.рт.ст.
Рассмотрим течение идеальной жидкости по горизонтальной трубе переменного сечения. Опыт показывает, что статическое давление в узкой части меньше, чем в широкой. Это явление связано с тем, что в узкой части трубы скорость выше, чем в широкой. Так как трубка расположена горизонтально, то уравнение Бернулли выглядит следующим образом:
P1 + (pυ12)/2 = P2 +(pυ22)/2
Так как сечение S, > S2, то на основании уравнения неразрывности струи υ2 > υ1. Чтобы сохранить равенство в уравнении Бернулли необходимо Р, > Р2. Если Р2 будет меньше атмосферного давления, тогда в систему будет засасываться воздух - это явление получило название гидродинамического парадокса. На основе этого явления в медицинской практике используется водоструйный насос и ингалятор. Они просты по устройству, бесшумны в работе, не требуют смазки, гигиеничны.
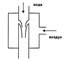

Пусть по горизонтальной трубе одинакового сечения движется реальная вязкая жидкость (Ньютоновская) под давлением Р. Так как давление на все слои одинаково, то можно ожидать одинаковую скорость движения всех слоев. Однако опыт показывает, что скорость слоев увеличивается к центру трубы. Если жидкость смачивает стенки трубы, то скорость первого слоя ровна нулю вследствие сильного взаимодействия молекул стенок трубки и молекул жидкости. В последующих слоях она увеличивается постепенно от слоя к слою, вследствие взаимодействия молекул жидкости друг с другом. Эти силы взаимодействия между слоями жидкости носят название сил внутреннего трения или сил вязкости. Они обусловлены:
1. Потенциальными силами взаимодействия между молекулами жидкости.
2. Перемещением молекул жидкости из одного слоя в другой.
Например: молекулы 3-го слоя, обладающие меньшей кинетической энергией по сравнению с молекулами 4-го слоя, перемещаясь в него, уменьшают общую кинетическую энергию, т.е. как бы затормаживают его.Было выяснено опытным путём, что силы внутреннего трения между слоями жидкости зависят:
1. От площади соприкасающихся слоев Fη ~ S
2. От градиента скорости Fη ~ dυ/dx
Физический смысл градиента скорости:
Градиентом любой физической величины называется изменение этой величины, отнесённое к расстоянию, вдоль которого это изменение происходит.
3. Силы внутреннего трения зависят от природы жидкости, так как молекулы различных жидкостей находятся на различных расстояниях и имеют различную скорость, а следовательно и кинетическую энергию. Эта зависимость учитывается коэффициентом вязкости - η. Таким образом, силы внутреннего трения зависят от природы жидкости, прямо пропорциональны градиенту скорости и площади соприкасающихся слоев.
Fη = η (dυ/dx)S
Эта формула получила название формулы Ньютона. Если площадь соприкасающихся слоев S = 1 и градиент скорости dυ/dx = 1, то Fтр = η
Коэффициентом вязкости или вязкостью жидкости называется величина численно равная силе трения, возникающей между двумя слоями жидкости, соприкасающимися на площади равной единице и при градиенте скорости между ними равным единице.
Коэффициент вязкости измеряется в системе СИ: η =Fηdx/Sdυ; Н м / м2 (м/с) = Н с / м2 = Па с
В системе СГС: Пуаз (Пз) = дн с / см2; Н с / м2 = 105 дн с / 104 см2 = 10 Пз. В медицине принято измерять вязкость в Пуазах. Коэффициент вязкости зависит не только от природы жидкости, но и от температуры. С повышением температуры коэффициент вязкости уменьшается. Это объясняется тем, что с повышением температуры расстояния между молекулами увеличиваются, а силы взаимодействия ослабляются.
Ввиду больших трудностей, возникающих при непосредственном измерении вязкости её определяют косвенным путём. Наибольшее применение имеют методы: падающего шарика и капиллярного визкозиметра. Метод падающего шарика основан на законе Стокса. Стокс установил, что на небольшое тело шаровидной формы, перемещающееся в жидкости, действует сила трения, прямо пропорциональная радиусу этого тела, его скорости и коэффициенту вязкости жидкости.
Fтр = 6πηrυ
Если бросить в жидкость металлический шарик диаметром 0,2—0,3 мм, то он будет двигаться в жидкости равномерно. На движущийся шарик будут действовать три силы
1. Сила тяжести Р = mg, направленная вертикально вниз.
2. Выталкивающая сила FB, направленная вертикально вверх.
3. Сила трения FTp, направленная также вертикально вверх.
По первому закону Ньютона тело двигается равномерно, если равнодействующая всех сил, действующих на него, равна 0.
Р = Fтр + Fв, откуда Fтр = Р - Fв
По закону Стокса Fтр = 6πηrυ,
P = mg; m = pTV; P=pTVTg =4/3 πr3pTg
По закону Архимеда Fвыт = pжVTg = 4/3 πr3ржg
6πηrυ=4/3 πr3g (pТ – pЖ) η=2/9 (gr2(pТ - pЖ)/υ)
Радиус шарика можно измерить с помощью микроскопа с окулярным микрометром, скорость движения шарика можно определить по формуле V = s /t, измерив линейкой s, а секундомером - t. Плотность вещества шарика и исследуемой жидкости найдём из специальных таблиц при заданной температуре. По приведенной формуле можно вычислить коэффициент вязкости. Метод требует большого количества жидкости, жидкость должна быть прозрачной. Метод довольно точен, используется в санитарии. В медицинской практике для определения коэффициента вязкости крови, спиномозговой жидкости и других биологических жидкостей пользуются методом капиллярного вискозиметра, основанный на законе Гагена-Пуазейля. Они установили, что объём жидкости, протекающей через поперечное сечение капилляра (R<1мм ) в единицу времени прямо пропорционален R4, dP/dl и обратно пропорционален η, коэффициент пропорциональности в системе СИ равен π/8.
Q=(πR4dP)/(8ηdl)
где dP/dl — градиент давления, dP — разность давлений в начале и в конце капилляра, dl — длина капилляра. При пропускании жидкостей через капилляры с одинаковым радиусом при одинаковом градиенте давления, получим:
V1/t = πR4/8η1dl объём 1 жидкости
V2/t = πR4/8η2dl объем 2 жидкости
Найдём относительную вязкость, поделив 1 выражение на 2.
V1/V2 - формула Гагена-Пуазейля.
Тогда число делений трубки (б) укажет относительную вякость. Зная η1, определим η2 по формуле:Кр = (Rсеη)/pD
где η - вязкость жидкости, р - плотность, D - диаметр трубки. Безразмерная величина Rсе называется числом Рейнольдса. Для гладких трубок Rсе = 2300, для трубок с шероховатыми поверхностями эта величина меньше. Течение крови в артериях при нормальных условиях является ламинарным. Турбулентность проявляется только в некоторых местах, например, за полулунными клапанами аорты. В некоторых , патологических случаях, при сужении кровеносных сосудов, пороках сердца, изменении коэффициента вязкости крови, турбулентность распространяется на более длинные участки артерии, что может служить диагностическим целям. При течении идеальной жидкости по горизонтальной трубе постоянного сечения гидростатическое давление в любом сечении одинаково (pgh1 = pgh2 =...), h1 = h2 = ..., динамическое давление так же одинаково в любом сечении (pυ12/ 2 = рυ22 / 2 =...), т.к. υ1 = υ2= ... по уравнению неразрывности струи. Следовательно и статическое давление постоянно по всей длине трубы на основании уравнения Бернулли (Р1 = Р2). Для реальной жидкости гидростатическое и динамическое давления в любом сечении одинаковы по той же причине, что и для идеальной жидкости. Однако уравнение Бернулли для реальной жидкости, как частный случай закона сохранения энергии, должно включать работу против сил трения.
P1V = P2V + ATP или P1V = P2V + FTPL
Следовательно, т. к. расстояние от начала трубы L увеличивается, то Р2 уменьшается. Это подтверждается и экспериментально. Манометрические трубки, вставленные в стенку трубы, измеряют статическое давление и оно постепенно уменьшается.
Величина градиента давления зависит:
1. От коэффициента вязкости жидкости, т.к. Fтр ~ η,
2.От скорости течения жидкости прямо пропорционально, т.к. сила сопротивления возрастает пропорционально скорости,
3. Если труба разветвляется, то от числа разветвлений - прямо пропорционально.
Движение жидкости по трубам с эластичными стенками отличается от движения жидкости по трубам с упругими стенками своей непрерывностью. Можно провести аналогию между законом Пуазейля и Ома для участка цепи
Q=(πr4dP)/(8ηL), J=U/R
Q=(dP)/X, X=(8ηL)/ (πr4) Гидравлическое сопротивление X пропорционально вязкости η, длине трубы L… Хо6щ = X1 + Х2 + Х3 + ... - при последовательном соединении,Моделирование. Механическая и электрическая модели кровообращения
Методы определения скорости кровотока
2. По эффекту Допплера. К поверхностному кровеносному сосуду, в котором необходимо определить параметры потока крови с помощью ультразвукового…Способы измерения давления крови
Энергия состоит из потенциальной энергии давления, которое должно быть создано вначале для преодоления сопротивления движению крови по всей… Эта энергия в соответствии с уравнением Бернулли для горизонтального…Aлж =PVуд + (mυ2)/2 + PVуд + (pυ2Vуд)/2 = (P + (pυ2)/2)Vуд
где Р - среднее давление, под которым кровь выбрасывается в аорту,
Р = 100 мм. рт. ст. = 105 100/760 Па = 1,3104Па
р = 1,05103кг/м3 - плотность крови
υА - скорость крови в аорте, в состоянии покоя υ ~ 0,5 м/с.
VД - ударный объем крови в покое - 60 см3 = 6 * 10-5 м3.
Тогда Aж =(1.3*104 + ((1.05*103*0.25)/2)6*10-5) ≈ 0.81 Дж
Учитывая работу правого желудочка, для сердца в целом получим: Аж = 1,2Аж = 1,280,81 = 1Дж
Время сокращения желудочков примерно гж = 0,3 с. Тогда мощность, развиваемая сердцем при сокращении, будет Nc =Ac/tж = 1/0.3 ≈ 3.3Вт
Считая в среднем 60 сокращений сердца в 1 мин., получим, что за 1 мин. сердце совершает работу Ам = 60 Дж. За сутки Ас = 86400 Дж. При расчете работы сердца можно учитывать минутный объем
Vм = Vудn
В нашем примере Vм = 60 Vуд = 60 * 60 = 3600 мл/мин - 3,6 л/мин.
При физической нагрузке работа сердца увеличивается более чем в 5 раз: Vm = 3,6 л/мин * 5 = 18 л/мин.
МЕДИЦИНСКАЯ ЭЛЕКТРОНИКА
1. Изучение медико-биологических и технических характеристик объекта исследования. 2. Физико-технических характеристик электронных устройств, применяемых в… В курсе нашей дисциплины для частичного решения указанных задач введен раздел "Медицинская…Диагностические электронные системы
Устройства съема медицинской информации (УСМИ) — это устройства, обеспечивающие получение сигналов, связанных с явлениями и процессами, происходящими в живых организмах.
Основные требования, предъявляемые к УСМИ.
1. Минимум искажения полезного сигнала.
2. Максимальная помехозащитность.
3. Удобство размещения в необходимом для измерения месте.
4. Отсутствие раздражающего действия.
5. Возможность многократного использования и стерилизации без изменения характеристик.
Электроды - это проводники специальной формы для съема электрических сигналов реально существующих в организме.
Классификация УСМИ
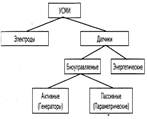
Различного вида электроды используются и для подведения к организму внешнего воздействия.
Электроды как устройства съема различаются:
1.По виду регистрируемого сигнала (ЭКГ, ЭМГ, ЭЭГ, ЭГГ, ЭОГ и др.).
2.По материалу (металлические, угольные, стеклянные). Стеклянные правильно называть электролитическими, т. к. проводником является раствор электролита (КС1 и др.), который заключен в стеклянную канюлю.
3.По конструкции (плоские, игольчатые, многоточечные).
4.По площади (чем меньше площадь, тем более локально отводятся биопотенциалы).
5.По назначению: одноразовые — используются в кабинете функциональной диагностики; длительного наблюдения - в палатах реанимации; динамического наблюдения - в физиологии труда и спорта; экстренного применения - скорая помощь.
6.По месту расположения (поверхностные и вкалывающие). Поверхностные электроды должны иметь контактное сопротивление 10-15 кОм, поэтому их накладывают через токопроводящие пасты и прокладки.
Очень часто приходится регистрировать изменение характеристик организма и окружающей среды, которые по своей природе не являются электрическими. Их называют входные неэлектрические величины, обусловленные жизненными функциями, к ним относятся:
1. Механические (перемещение, скорость, ускорение, акустические параметры, давление, вибрации и др.).
2. Физические (тепловые: температура, энергия, количество теплоты; электрические: характеристики электрического (Е, ε, у), магнитного поля (B, μ ,v), импеданс и др.; оптические: показатель преломления, сила света, освещенность, яркость; атомные и ядерные: спектральный состав, масса атомов и ядер, активность излучения, дозы и др.).
3. Химические (химический состав, концентрация, рН).
4. Физиологические (кровенаполнение, пульс и др.).
Для измерения этих величин используются датчики (преобразователи).
ДАТЧИКИ— это УСМИ, которые своим чувствительным элементом реагируют на воздействие измеряемой величины и осуществляют преобразование этого воздействия в форму, удобную для последующего усиления, регистрации, обработки (как правило в электрические сигналы)
В энергетических датчиках создается смодулированный (с неменяющимися параметрами) поток энергии. Измеряемый параметр изменяет этот поток (модулирует), эти изменения регистрируются чувствительным элементом. Таким образом, общую схему измерения энергетическими датчиками можно представить так: источник энергии - объект исследования - чувствительный элемент.


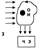
В фотоэлектрическом датчике (1) создается световой поток Фо. При прохождении через ткани организма поток меняется, в качестве регистрирующего устройства может использоваться фоторезистор, фотоэлемент, фотопластинка. В рентгеновских датчиках (аппаратах) (2) в качестве излучения используются рентгеновские лучи, а в качестве чувствительного элемента - фотопластинка, люминесцентный экран, рентгеночувстительный экран. При ультразвуковом исследовании - (УЗИ) (3) используется поток УЗ-волн, а для регистрации, как правило, пьезодатчики. В биоуправляемых активных (генераторных) датчиках под воздействием измеряемой величины генерируются пропорциональные ей электрические сигналы. Наиболее часто употребляемые датчики: термопары (1), тензодатчики (2), индукционные (3), полупроводниковые вентильные фотоэлементы (4).

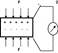


В термопарах имеются два спая, в которых соединяются два различных проводника или полупроводника. В каждом из спаев создаются контактные разности потенциалов. Суммарная разность потенциалов определяет ЭДС термопары. ЭДС пропорциональна разности температур спаев ε = к (Т1 - Т2), где к зависит от типа соединяемых проводников или полупроводников. В тензодатчиках используется прямой пьезоэлектрический эффект - при воздействии на некоторые кристаллы (кварца, титанат бария и других) внешней силой, в результате структурной поляризации, на поверхности этих кристаллов появляется разность потенциалов, пропорциональная приложенной силе. В индукционных датчиках, при перемещении постоянного магнита относительно катушки, возникает ЭДС индукции, которая определяется по закону Фарадея ε = - ∆Ф/∆t. В конечном итоге ЭДС пропорциональна скорости перемещения постоянного магнита. В полупроводниковых вентильных фотоэлементах используются кристаллы селена. Внутри селеновой пластины за счет технологии изготовления создается запирающий слой, который не пропускает основных носителей заряда. При освещении фотоэлемента в верхнем слое возникают пары электрон-дырка. За счет запирающего слоя они разделяются и образуется фото ЭДС, пропорциональная световому потоку.
Биоуправляемые пассивные (параметрические) датчики представляют собой замкнутую электрическую цепь, в состав которой входят: источник постоянного или переменного напряжения, измерительный прибор (амперметр) и сопротивление R, величина которого меняется пропорционально изменению измеряемого
неэлектрического сигнала организма. По закону Ома пропорционально изменяется и ток в цепи, поэтому шкала измерительного прибора градуируется в единицах измеряемой неэлектрической величины. По виду сопротивления параметрические датчики подразделяются на: резистивные, емкостные, индуктивные и контактные.
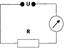
В резистивных датчиках используются: активное переменное сопротивление, движок которого перемещается пропорционально механическому перемещению органов тела человека; терморезистор, величина которого меняется пропорционально температуре измеряемого объекта; фоторезистор, его сопротивление меняется при изменении светового потока; в качестве сопротивления можно подключать непосредственно ткани организма. В этом случае измеряется импеданс (общее сопротивление ткани переменному току). В емкостныхдатчиках сопротивлением является конденсатор. Как известно емкость конденсатора определяется формулой: C = (εε0S)/(4πd),
а величина емкостного сопротивления R = 1/(ωC)
Таким образом, емкостное сопротивление будет меняться при изменении относительной диэлектрической проницаемости (е), площади пластин (S), расстояния между пластинами (d). Величина этих параметров меняется, либо при механической перемещении частей тела, либо при изменении влажности и температуры среды между пластинами конденсатора. В индуктивных датчиках используется катушка с ферромагнитным сердечником. Ее индуктивность (L) зависит от магнитной проницаемости сердечника (μ), числа витков катушки (n), размеров катушки (d,l). Величина индуктивного сопротивления определяется формулой RL = ωL. В контактных датчиках вместо сопротивления используются два контакта, которые замыкаются или размыкаются при периодическом движении, например, при изменении размеров грудной клетки при вдохе и выдохе. Для правильного использования датчиков необходимо знать их метрологические характеристики. Датчики должны периодически проверяться метрологическими службами. К метрологическим характеристикам относятся:
1. Чувствительность - это изменение выходного сигнала при изменении входного сигнала на единицу. Например, чувствительность термопары определяется формулой: k =∆ε/∆t
2. Предел чувствительности - минимальное значение изменения входного сигнала, которое можно зарегистрировать с помощью датчика.
3. Динамический диапазон - диапазон входных неэлектрических величин от предела чувствительности до максимального значения, регистрируемого датчиком без искажения.
4. Погрешность - разность между измеренным и действительным значением величины.
5. Время реакции (инерционность) показывает, на сколько величина выходного сигнала датчика отстает по времени (по фазе) от входного.
В качестве примеров использования датчиков рассмотрим измерение температуры, параметров системы дыхания и сердечнососудистой системы. Различают температуру поверхности и температуру ядра тела. Температура поверхности тела зависит не только от состояния организма, но и от внешней среды: температуры и давления воздуха, его влажности. Поэтому, как правило, температуру поверхности измеряют с точки зрения симметричности температурных полей левой и правой области тела человека. Температура ядра является более стабильным показателем и она определяется в основном состоянием внутренней среды организма. Измеряют температуру ядра непосредственным помещением датчика в мышцу и отдельные органы, ректальную температуру, в полости рта, в подмышечной впадине, паховой области, пупочной ямке. Для измерения температуры человеческого тела в качестве датчиков используются: полупроводниковые термосопротивления (термисторы), и термоэлементы (термопары).
Основными параметрами, измеряемыми в системе дыхания, являются частота дыхания и глубина дыхания. Измерение этих параметров производится по механическому перемещению грудной клетки и по противоположно направленным потокам воздуха при вдохе и выдохе, имеющими разную температуру и влажность. Механические перемещения грудной клетки оценивают контактными и резистивными (с активным сопротивлением) датчиками. Потоки воздуха измеряют емкостными датчиками, термисторами, термопарой. Для оценки деятельности сердечно-сосудистой системы используются неэлектрические параметры: частота пульса, параметры пульсовой волны, систолическое и диастолическое давление, тоны и шумы сердца, механические перемещения органов и тканей, связанные с одномоментым выбрасыванием ударного объема крови из левого желудочка и др. Частоту пульса и пульсовые волны (сфигмография) измеряют тензодатчиками. Механические перемещения грудной клетки в области верхушечного толчка (сейсмография) оценивают индукционными датчиками. Тоны и шумы сердца (фонокардиография) измеряют с помощью микрофонов, которые по сути представляют также датчики индукционной системы. Для измерения давления используют тензодатчики, основанные на пьезоэффекте. Эти датчики вносят в крупные кровеносные сосуды и в полости сердца. Исследование кровенаполнения и оценка тонуса кровеносных сосудов (плетизмография) производится импедансометрическими датчиками, энергетическими, фотоэлектрическими и тензодатчиками. Определение скорости кровотока производится энергетическими ультразвуковыми датчиками, метод измерения основан на эффекте Допплера.
Электрические сигналы на выходе УСМИ, как правило, имеют малую величину (амплитуду). Для регистрации их необходимо усилить. Для этих целей используются устройства усиления (УУ).
Устройства усиления напряжения, тока, мощности электрических колебаний за счет энергии постороннего источника называются усилителем колебаний.
Элементной основой усилителя является триод, вакуумный или полупроводнковый… 1.Колебания входного напряжения на сетке лампы создают пропорциональные колебания анодного тока (в случае…Лечебные электронные системы
Идеальный колебательный контур состоит из катушки индуктивности и конденсатора. Если зарядить конденсатор такого…T/t
Для получения импульсов других форм используются дифференцирующие и интегрирующие цепочки. Это последовательно соединенные конденсатор и активное сопротивление. Цепочки характеризуются
постоянной τ = R С. Величина этой константы и определяет форму импульса. Физиологический эффект воздействия импульсов тока состоит в том, что на каждый отдельный импульс ткань отвечает адекватным ответом (раздражением). Для каждой ткани в координатах амплитуда — длительность импульса определяют границу раздражения.

Выше кривой существует адекватный ответ, ниже ткань не раздражается. С этой точки зрения существуют физиологические параметры раздражения:
1. Реобаза (Аm) - это минимальная амплитуда импульса при бесконечно большой его длительности, которая вызывает адекватный ответ.
2. Хроноксия (tm) - это минимальная длительность импульса при двойной реобазе, которая вызывает адекватный ответ.
3. Лабильность (vmin) - это минимальная частота импульсов, на каждый из которых ткань отвечает адекватным ответом. Выше этой частоты (так называемый гладкий тетанус) ткань "не успевает" расслабится и находится в постоянном раздражении.
4. Адаптация (S) - связана со временем нарастания переднего фронта импульсов (крутизны). При некоторой достаточно малой крутизне ткань не отвечает адекватным ответом, хотя реобаза, хроноксия и лабильность соответствует граничной.
Врачу необходимо знать физические параметры импульсов возбудимости для грамотного и эффективного использования их для лечения заболеваний.
Электростимуляция импульсными токами используется:
1. Для компенсации временно утраченной функции (например, при потере электровозбудимости мышцы в результате травмы).
2. Для усиления функции (например, при значительной утрате функции сокращения миокарда больному "вшивают" генератор прямоугольных импульсов — стимулятор сердечной деятельности).
3. В некоторых случаях стимуляция используется при полной утрате функции.
4. Для подавления функции (аппарат электросон, электроанальгезия родов и др.).
Магнитотерапия- это воздействие на ткани организма постоянным или переменным низкочастотным магнитным полем (МП). Для этих целей используются постоянные магниты (магни-тоэлласты) и соленоиды (катушки индуктивности), на которые подается постоянное или переменное, порядка 50 Гц, электрическое напряжение. Механизм размена энергии магнитного поля (первичный эффект) далеко не выяснен. Однако благодаря усилиям медиков и магнитобиологов в последние годы выявлены многие физиологические эффекты при действии магнитного поля на биообъекты. Магнитное поле действует на парамагнитные элементы тканей, такие как О, Fe, Mn, которые участвуют в окислительных реакциях, что ведет к улучшению обменных процессов. Значительно усиливаются ионизационные процессы в МП, усиливается движение заряженных частиц и силы трения о клеточную мембрану, что повышает проницаемость ее, усиливает внутриклеточный и межклеточный обмен. Обнаружено также, что магнитотерапия обладает ярко выраженным противовоспалительным, анальгезирующим и противоотечным действием, способствует улучшению трофики, ускорению процессов регенерации тканей, эпитализации язвенных поверхностей, более быстрому заживлению ран. Действие МП ведет к увеличению количества функционирующих капилляров, кровонаполнению, ускорению тканевого кровотока, улучшению насыщения артериальной крови кислородом и т. д. В результате исследования последних лет обнаружено, что главным в механизме действия МП на молекулярном уровне является блок: белок — ионное окружение — вода, на тканевом и органном уровне основной точкой воздействия является микро-циркуляторное русло.
Метод лечебного воздействия постоянным током небольшой величины (напряжение 60—80 В) носит название гальванизация. Первичное действие постоянного тока на ткани организма связано с перераспределением ионов на полупроницаемых и не проницаемых тканевых перегородках — это явление называют поляризацией. Перераспределение ионов приводит к функциональным сдвигам в различных элементах тканей. Аппарат для гальванизации представляет собой двухполупериодный выпрямитель 1 со сглаживающим фильтром 2 и регулирующе- регистрирующей частью 3.

При проведении процедуры, во избежание прижигающего действия продуктами электролиза и лучшего контакта с кожей, под электроды помещают марлевые прокладки, смоченные физраствором. Оптимальный ток для проведения процедуры определяется только по ощущению пациента - легкое покалывание под электродами. Одновременно с гальванизацией часто используют введение лекарственных и питательных веществ в организм (ионы йода, металлы, пенициллин и др.) в ионном виде. Этот метод называют ионогальванизацией или лечебным электрофорезом. Препарат вводится с электрода, знак которого имеют вводимые ионы: с катода - катионы, с анода анионы.
Воздействие ультразвуком частотой 880 кГц и 2640 кГц называется ультразвуковой терапией. Воздействие осуществляется через специальные звукопроводящие пасты. В современных УЗ-аппаратах
интенсивность меняется в пределах (0,1 - 1,6) Вт / см2. Различают три вида первичных эффектов при действии ультразвука на живые ткани: механический, тепловой, химический. Механическое действие обусловлено колебанием частиц ткани (микромассаж). При этом происходит изменение взаимного расположения клеточных структур, что приводит к изменению их функций. Тепловое действие связано с поглощением УЗ - энергии в мышечных и особенно костных тканях, в первую очередь, при кавитационных явлениях. Химическое действие проявляется в изменении интенсивности окислительных процессов, усилении диффузии и др. Отдельное место среди лечебных методов занимают физические явления, возникающие в газах и газовых смесях. Всем известно, что в обычных условиях атомы и молекулы газов являются нейтральными, не заряженными. Превращение нейтральных атомов в заряженные частицы осуществляется под действием физико-химических факторов, таких как реакция горения, электрические разряды, различного вида излучения. Ионизационный эффект определяется:
1. Свойствами самих атомов, так называемой энергией ионизации. Эта энергия величина табличная и весьма значительно различается для различных газов.
2. Свойствами излучения - интенсивностью ионизации: количеством пар ионов, возникающих в единице объема газа за единицу времени под действием ионизатора.
В первую очередь рассмотрим процессы, возникающие в окружающей нас газовой среде — атмосферном воздухе. Известно, что в 1см3 воздуха постоянно присутствует около 1000 пар ионов, однако воздух при этих условиях не является проводником, т.к. всего в 1см3 воздуха присутствует 2, 7 1019 атомов и молекул, и 1000 пар ионов образуют слишком слабый ток. Вопрос состоит в том, откуда берутся эти ионы? Выявлено, что на молекулы воздуха постоянно действуют два вида физических факторов, так называемые постоянно действующие ионизаторы.
1. В почве, воздухе, воде всегда присутствуют радиоактивные элементы, излучения которых в виде α, β, γ, - излучений и создают ионы воздуха. Интенсивность ионизации радиоактивного излучения 8 пар/ (см3с).
2. Космические лучи. Первичные космические лучи это частицы с огромной энергией (порядка 10'°- 1018 эВ), которые "прилетают" к нам из космического пространства. Они взаимодействуют только с атомами верхних слоев атмосферы, разбивая их. В результате такого взаимодействия возникают вторичные космические лучи, которые подразделяются на жесткие и мягкие. К жестким относится: поток промежуточных по массе частиц - мезонов, к мягким - электроны, γ - фотоны. Вторичные космические лучи достигают поверхности земли и создают 2 пары ионов/ (см3с). Таким образом, постоянно действующие ионизаторы создают 10 пар ионов в 1см3 воздуха за 1 с. В воздухе как и в любом газе существует и обратный процесс - рекомбинация. При достижении около 1000 пар ионов в 1см3 процессы ионизации и рекомбинации уравниваются. Что же из себя представляют ионы воздуха или, как их называют, аэроионы? Различают легкие и тяжелые аэроионы. Легкие аэроионы это мелкие заряженные частицы воздуха (ионы, частицы воды), окруженные полярными молекулами воздуха. Тяжелые аэроионы это частицы дыма, пыли, на которые осаждаются легкие аэроионы. И легкие и тяжелые аэроионы, могут быть как положительными так и отрицательными. Тяжелые аэроионы оказывают отрицательное действие на организм. Из легких лечебное действие оказывают только легкие отрицательные аэроионы. Для характеристики здоровости атмосферного воздуха вводится специальная величина - коэффициент униполярности.
k = n+/n-
где n+ - концентрация легких положительных аэроионов, n- — концентрация легких отрицательных аэроионов. В чистом загородном воздухе k = 1-1,2, у фонтанов, водопадов, у моря k < 1, в пещерах, подземельях, в плохо проветриваемых помещениях к достигает 10—20.
Метод воздействия легкими отрицательными аэроионами с лечебными целями называют аэроионотерапией.
1.Чистый сухой воздух продувают через аэродинамическую трубу. В начале трубы находится радиоактивный препарат, излучение которого активно… 2.Получение аэроионов возможно при механическом дроблении воды, так… 3. Третий способ основан на электроэффлювивальном эффекте - это образование аэроионов в электрическом поле большой…ГЕОМЕТРИЧЕСКАЯ ОПТИКА. ФОТОМЕТРИЯ. ФОТОЭФФЕКТ
Изучая окружающий мир, человечество накопило большое количество экспериментальных сведений о свете. Отражение и прямолинейность распространения…Законы отражения
Среда, во всех точках которой скорость распространения света одинакова, называется оптически однородной средой. Границей двух сред называется поверхность, разделяющая две оптически неоднородные среды. Угол α между лучом падающим и перпендикуляром, восстановленным к границе двух сред в точке падения, называется углом падения. Угол β между лучом отраженным и перпендикуляром, вое-становленным к границе раздела двух сред в точке падения, называется углом отражения.

I закон: Луч падающий, перпендикуляр, восстановленный к границе раздела двух сред в точке падения, и луч отраженный лежат в одной плоскости.
II закон: Угол падения равен углу отражения: α = β
Различают отражения зеркальное и диффузное. Зеркальным называется отражение, при котором падающий на поверхность параллельный пучок лучей остается параллельным. Диффузным называется отражение, при котором падающий параллельный пучок лучей рассеивается.
Законы преломления
На границе двух сред, кроме отражения, наблюдается преломление света — явление, состоящее в том, что луч частично проходит во вторую среду, изменяя свое первоначальное направление. Этот луч называется преломленным.
Угол у между лучом преломленным и перпендикуляром к границе раздела двух сред в точке падения называется углом преломления.
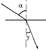
I закон: Луч падающий, перпендикуляр, восстановленный к границе раздела двух сред в точке падения, и преломленный луч лежат в одной плоскости.
I I закон: Отношение синуса угла падения к синусу угла преломления есть величина постоянная для данных двух сред и называется показателем преломления второй среды относительно первой:
sinα/sinγ = const = n21
Показатель преломления какой-либо среды относительно вакуума называется абсолютным показателем преломления (n).Если угол падения больше угла преломления, то вторая среда называется оптически более плотной, чем первая.При переходе света из оптически более плотной среды в оптически менее плотную среду угол падения α будет меньше угла преломления γ.

Поэтому, при некотором угле падения (αпр.) угол преломления окажется равным 90°, т.е. преломленный луч будет скользить вдоль границы раздела сред, не входя во вторую среду.
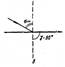
При дальнейшем увеличении α свет будет полностью отражаться в первую среду. Это явление носит название полного внутреннего отражения света. Угол αПР называется предельным углом падения.
sinαпр/sin900 = n2/n1 = n21, откуда sinαпр = n21
Исходя из этих соотношений, можно определять относительный показатель преломления двух сред, а также абсолютный показатель преломления одной из сред, если показатель другой среды известен. Оптический прибор, служащий для этой цели и основанный на явлении полного внутреннего отражения, называется рефрактометром.
Линзы
Для изменения направления световых лучей в оптических системах широко используют линзы (от латинского слова Lens - чечевица).
Линзой называется прозрачное тело, ограниченное двумя сферическими поверхностями, и по показателю преломления отличающееся от окружающей среды.
Мы будем рассматривать только тонкие линзы, толщина которых пренебрежимо мала в сравнении с радиусами сферических поверхностей, ограничивающих линзу. Принято считать, что в таких линзах преломление лучей происходит в одной плоскости (ПП), которая называется преломляющей.
Прямая, проходящая через центры сферических поверхностей, ограничивающих линзу, (SS') называется главной оптической осью. Точка пересечения главной оптической оси с преломляющей плоскостью называется оптическим центром линзы (О). Любая прямая, проходящая через оптический центр линзы, называется оптической осью (АА). Лучи, параллельные главной оптической оси, после преломления в линзе собираются в одной точке, называемой главным фокусом линзы (F). Точка пересечения оптической оси с фокальной плоскостью называется побочным фокусом (F').

Такие линзы называются собирающими. Параллельный пучок лучей после преломления в линзе может рассеиваться, тогда в одной точке, называемой мнимымфокусом, соберутся продолжения этих лучей. Такие линзы называются рассеивающими.

Плоскость, перпендикулярная главной оптической оси и проходящая через главный фокус линзы, называется фокальной плоскостью.
Если предмет находится между фокусом и двойным фокусом, изображение - действительное, обратное, увеличенное.Микроскоп
Расстояние ∆ = F1F2 между задним фокусом объектива и передним фокусом окуляра называется оптической длиной тубуса микроскопа.
Увеличение объектива выражается формулой: Гок = ∆/Fок
Для окуляра: Гок = L/Fок
Общее увеличение микроскопа равно произведению увеличений объектива и окуляра:
Гм = ГобГок = ∆L/FобFок
В зависимости от характера и свойств изучаемого препарата, в микроскопии применяются специальные методы наблюдения. Метод светлого поля в проходящем свете применяется при исследовании прозрачных препаратов с включенными в них поглощающими частицами и деталями. Пучок лучей, проходя через препарат, дает равномерно освещенное поле в плоскости изображения. Если в препарате имеется поглощающий свет объект, то он частично рассеивает его, что и обуславливает возникновение изображения. Метод светлого поля в отраженном свете применяется для наблюдения непрозрачных объектов. Метод темного поля в проходящем свете применяется в биологии, главным образом, для получения изображений непрозрачных объектов. Пучок лучей, освещающих препарат, не попадает непосредственно в объектив. Изображение создается только светом, рассеянным микрочастицами. В поле зрения на темном фоне видны изображения частиц, отличающихся от окружающей среды по показателю преломления. Метод темного поля в отраженном свете осуществляется освещением непрозрачного препарата сверху специальной системой, расположенной вокруг объектива. Метод наблюдения в поляризованных лучах применяется в проходящем и отраженном свете для исследования под микроскопом объектов, обладающих двойным лучепреломлением. Препарат освещается поляризованным светом. Видоизмененный поляризованный свет, прошедший через препарат, изучается с помощью анализаторов и компенсаторов различного устройства.
Метод фазового контраста служит для получения изображений прозрачных и бесцветных объектов, невидимых при обычных методах микроскопии. Метод основан на том, что показатели преломления объекта и среды различны, вследствие чего световая волна, прошедшая сквозь объект, претерпевает изменения по фазе и приобретает, так называемый "фазовый рельеф». Эти фазовые изменения преобразуются специальным фазово - контрастным устройством в изменения амплитуд, что приводит к ослаблению или усилению интенсивности света, прошедшего через объект. В результате получается видимое контрастное изображение структуры препарата, в котором распределение яркостей (амплитуд) воспроизводит указанный выше фазовый рельеф. Метод микропроекции и микрофотографии применяется для наблюдения или исследования изображения объекта на экране или на фотоматериале. При этом, чтобы получить действительное изображение объекта, с помощью специальных устройств увеличивают длину тубуса микроскопа так, что промежуточное изображение А1В1, находится немного дальше переднего фокуса окуляра, а изображение (действительное, обратное и увеличенное) получается за окуляром на экране или фотопленке.
Оптическая система глаза
Недостатки оптической системы глаза и их устранение
Близорукость - недостаток глаза, состоящий в том, что, при отсутствии аккомодации, изображение предмета лежит впереди сетчатки; в случае…Фотометрия. Фотоэффект
Основной фотометрической величиной является световой поток - это среднее количество световой энергии, проходящей за единицу времени через заданную поверхность.
Ф = dW/dt
Здесь dW — количество энергии, проходящей через заданную поверхность за время dt. Понятие силы света вводится с помощью представления о точечном источнике света. Источник света считается точечным, если его размеры малы в сравнении с расстоянием до места наблюдения и если он испускает свет равномерно по всем направлениям.
Сила света измеряется световым потоком, создаваемым точечным источником света в единичном телесном угле ω.
J = Ф/ω
Телесным углом называется часть пространства, ограниченная конической поверхностью и измеряемая отношением площади S, вырезаемой этим углом на поверхности сферы, к квадрату радиуса сферы R:
ω = S/R2
Единицей измерения телесного угла является стерадиан (пространственный радиан) ср - угол, вырезающий единичную площадь на сфере единичного радиуса. Очевидно, что телесный угол, охватывающий все пространство вокруг источника света, равен: ω = 4π.
По логике построения фотометрии, в качестве основной единицы надо было выбрать единицу светового потока. Но исторически сложилось в качестве основной единицы использовать единицы силы света. Первоначально эта единица - 1 свеча - определялась, как определенная часть силы света эталонной лампы. В настоящее время единицей силы света в СИ является кандела (Кд).
Кандела - это сила света, испускаемого с поверхности площадью 1/600000 м2 полного излучателя в перпендикулярном направлении при температуре излучателя, равной температуре затвердевания платины, под давлением 101325 Па.
Единицей светового потока в СИ является люмен (лм). Один люмен - световой поток, испускаемый точечным источником силой света 1 Кд внутри телесного угла 1 ср: 1лм = 1Кд*1ср
Для количественной оценки освещения поверхностей вводится понятие освещенности.Освещенностью поверхности называется величина, измеряемая световым потоком, падающим на единицу этой поверхности.
E = dФ/dS
Если освещенность всех точек одинакова, то Е = Ф / S , где Ф - световой поток, равномерно распределенный по поверхности S. Единица освещенности в СИ называется люксом (лк). Один люкс — освещенность поверхности световым потоком 1 лм, равномерно распределенным по площади 1 м2.
Иногда применяется единица освещенности один фот - освещенность поверхности световым потоком 1 лм, равномерно распределенный по площади 1 см2.
Лк = 1 лм / 1 м2 =1 лм / 10000 см2 = 10-4 фот.
Первый закон освещенности:
Освещенность точечным источником поверхности, нормально падающими лучами, прямо пропорциональна силе света источника и обратно пропорциональна квадрату расстояния от источника до освещаемой поверхности.
E0 =Ф0/S0 = 4πJ/4πR2 = J/R2
Второй закон освещенности:
Освещенность поверхности наклонным световым потоком прямо пропорциональна косинусу угла падения лучей.
Е = E0cosα
Если вместо Ео во второй закон освещенности подставить его значение из первого закона, то
Е = (J / R2) cosα.
Это выражение называется объединенным законом освещенности.
До сих пор мы говорили только о точечных источниках света. Однако во многих случаях источники света являются протяженными; при рассмотрении таких источников глаз различает их форму и размеры. Для протяженных источников сила света уже не может служить достаточной характеристикой. В самом деле, из двух источников, излучающих свет одинаковой силы, но имеющих различные размеры (площади), меньший источник кажется более ярким, так как он дает большую силу света с единицы площади.
Поэтому для протяженных источников света вводится дополнительная характеристика, называемая яркостью. Яркость протяженного источника света измеряется силой света, излучаемой с единицы площади видимой поверхности этого источника в перпендикулярном направлении.
B = J/S
В системе СИ яркость измеряется в нитах (нт): 1 нт = 1 Кд / м2 . Внесистемная единица - стильб (ст): 1ст = 1 Кд / см2= 104 нт.
Фотоэффект
Фотоэффектом называется освобождение (полное или частичное) электронов от связей с атомами и молекулами вещества под воздействием различного вида излучений.
Если электроны выходят за пределы освещаемого вещества (полное освобождение), то фотоэффект называется внешним. Если же электроны теряют связь только со своими атомами и молекулами, но остаются внутри освещаемого вещества, увеличивая тем самым электропроводность, то фотоэффект называется внутренним. Внешний фотоэффект наблюдается у металлов, а внутренний чаще всего у полупроводников. Экспериментальные исследования, выполненные А.Г. Столетовым, а так же другими учеными, привели к установлению следующих основных законов внешнего фотоэффекта.
I закон: Фототок насыщения J (т.е. максимальное число электронов, освобождаемых светом в 1с) прямо пропорционален световому потоку Ф.
J = kФ
Где k - коэффициент пропорциональности, называемый фоточувствительностью освещаемой поверхности и измеряется мкА / лм.
II закон: Скорость фотоэлектронов пропорционально возрастает с увеличением частоты падающего света и не зависит от его интенсивности.
III закон: Независимо от интенсивности света, фотоэффект начинается только при определенной (для данного металла) минимальной частоте света или максимальной длине волны, называемой красной границей фотоэффекта.
Законы внешнего фотоэффекта получают простое истолкование на основе квантовой теории света. По этой теории, величина светового потока определяется числом световых квантов (фотонов), падающих в единицу времени на поверхность металла. Каждый фотон может взаимодействовать только с одним электроном. Поэтому максимальное число фотоэлектронов должно быть пропорционально световому потоку (первый закон фотоэффекта). Энергия фотона hv, поглощенная электроном, частично расходуется на совершение работы выхода электрона из металла А; оставшаяся часть этой энергии идет на сообщение ему кинетической энергии mυ2/2. Тогда, согласно закону сохранения энергии, можно записать:
Hv = A + (mυ2)/2
Эта формула, предложенная в 1905 году Эйнштейном и подтвержденная затем многочисленными экспериментами, называется уравнением Эйнштейна. Из этого уравнения непосредственно видно, что скорость фотоэлектрона возрастает с увеличением частоты света и не зависит от его интенсивности (поскольку ни А, ни v не зависят от интенсивности света). Этот вывод соответствует второму закону фотоэффекта. Кроме того, из уравнения Эйнштейна следует, что с уменьшением частоты света кинетическая энергия фотоэлектронов уменьшается (величина А постоянна для данного освещаемого металла). При некоторой достаточно малой частоте v = vmin (или длине волны λmax= с / vmin) кинетическая энергия фотоэлектрона станет равной нулю (mυ2)/2= 0 и фотоэффект прекратится (третий закон фотоэффекта). Это будет иметь место при hvmin = A, т.е. в случае, когда вся энергия фотона расходуется на совершение работы выхода электрона. Тогда: vmin = A/h, или λmax = hc/A
Эти формулы определяют красную границу фотоэффекта и что она зависит от величины работы выхода, т.е. от рода металла. На внешнем фотоэффекте основан важный физико-технический прибор, называемый вакуумным фотоэлементом. Катодом К служит слой металла, нанесенный на внутреннюю поверхность стеклянного баллона, из которого выкачан воздух. Анод А выполнен в виде металлического кольца, помещенного в центральной части баллона. При освещении катода, в цепи фотоэлемента возникает электрический ток за счет электронов, выбитых из катода. Сила тока пропорциональна величине светового потока, падающего на катод. Большинство современных фотоэлементов имеют сурьмяно-цезиевые или кислородно-цезиевые катоды, обладающие высокой фоточувствительностью. Первые чувствительны к видимому и ультрафиолетовому свету, а вторые к инфракрасному и видимому свету. В некоторых случаях, для увеличения чувствительности фотоэлемента, его наполняют аргоном при давлении порядка 10-2 мм.рт.ст. Фототок в таком фотоэлементе усиливается вследствие ионизации аргона, вызванной столкновением фотоэлектронов с атомами аргона. Внутренний фотоэффект наблюдается у полупроводников и, в меньшей мере, у диэлектриков. Полупроводниковая пластинка присоединяется к полюсам батареи. Ток в цепи незначителен, поскольку полупроводник обладает большим сопротивлением. Однако при освещении пластинки ток в цепи резко возрастает. Это обусловлено тем, что свет вырывает электроны из атомов полупроводника, которые, оставаясь внутри полупроводника, увеличивают его электропроводность. Такое сопротивление называют фоторезистор. На явлении внутреннего фотоэффекта основана работа полупроводниковых фотоэлементов. Для их изготовления используют селен, сернистый свинец, сернистый кадмий и некоторые другие полупроводники. Фоточувствительность полупроводниковых фотоэлементов в сотни раз превышает фоточувствительность вакуумных фотоэлементов. Некоторые фотоэлементы обладают отчетливо выраженной спектральной чувствительностью. У селенового фотоэлемента спектральная чувствительность очень близка к спектральной чувствительности человеческого глаза. Недостатком полупроводниковых фотоэлементов является их заметная инерционность: изменение фототока запаздывает относительно изменения освещенности фотоэлемента. Поэтому полупроводниковые фотоэлементы не пригодны для регистрации быстроизменяющихся световых потоков. В качестве примера полупроводникового фотоэлемента рассмотрим устройство селенового вентильного фотоэлемента.
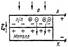 Он состоит из металлической подложки, дырочного полупроводника, покрытого прозрачным слоем металла (обычно тонкий слой золота). На границе металл-полупроводник, вследствие диффузии, возникает контактный запирающий слой с напряженностью Ек. Включим теперь световой поток Ф, проникающий в полупроводник. Благодаря внутреннему фотоэффекту увеличивается концентрация свободных зарядов обоих знаков - электронов и дырок. Электроны свободно диффундируют через контакт, а для дырок он действительно является запирающим слоем. В результате при освещении электроны накапливаются на подложке, а дырки - в полупроводнике. Между контактами А и К возникает разность потенциалов
Он состоит из металлической подложки, дырочного полупроводника, покрытого прозрачным слоем металла (обычно тонкий слой золота). На границе металл-полупроводник, вследствие диффузии, возникает контактный запирающий слой с напряженностью Ек. Включим теперь световой поток Ф, проникающий в полупроводник. Благодаря внутреннему фотоэффекту увеличивается концентрация свободных зарядов обоих знаков - электронов и дырок. Электроны свободно диффундируют через контакт, а для дырок он действительно является запирающим слоем. В результате при освещении электроны накапливаются на подложке, а дырки - в полупроводнике. Между контактами А и К возникает разность потенциалов
- фото-э.д.с, величина которой пропорциональна освещенности проводника. Таким образом, вентильный фотоэлемент представляет собой генератор тока, непосредственно преобразующий световую энергию в электрическую. В качестве полупроводников в вентильном фотоэлементе используют селен, закись меди, сернистый таллий, германий, кремний. В вентильном фотоэлементе могут применяться два полупроводника с различными типами проводимости - электронной и дырочной. Весьма перспективным является практическое использование вентильных фотоэлементов в качестве генераторов электроэнергии. Батареи кремниевых фотоэлементов, получивших название солнечных батарей, применяются на космических спутниках и кораблях для питания различной электронной аппаратуры. Некоторые вентильные
фотоэлементы чувствительны к инфракрасному излучению, их применяют для обнаружения нагретых невидимых тел, т.е. как бы расширяют возможности зрения. Исключительно велико значение фотоэлементов для телемеханизации и автоматизации производственных процессов. В сочетании с электронным усилителем и реле, фотоэлемент является неотъемлемой частью автоматических устройств, которые, реагируя на световые сигналы, управляют работой различных промышленных и сельскохозяйственных установок и транспортных механизмов. На внешнем фотоэффекте основана работа электронно-оптического преобразователя (ЭОП), предназначенного для преобразования изображения из одной области спектра в другую, а также для усиления яркости изображений. В медицине ЭОП применяют для усиления яркости рентгеновского изображения, это позволяет значительно уменьшить дозу облучения человека. Если сигнал с ЭОП подать в виде развертки на телевизионную систему, то на экране телевизора можно получить "тепловое" изображение предметов. Части тела, имеющие разные температуры, различаются на экране либо цветом, при цветном изображении, либо светом, если изображение черно-белое. Такая система, называемая тепловизором, используется в термографии.
ВОЛНОВАЯ ОПТИКА
Почти одновременно с корпускулярной теорией света (1678- 1690 г.) голландский физик Гюйгенс опубликовал "Трактат о свете", в котором… В своем труде Гюйгенс дал принципы распространения волнового процесса в…Каждая точка среды, до которой дошло световое возбуждение, сама становится источником вторичных световых волн, огибающая к которым в каждый данный момент времени является фронтом распространения световых волн. Под фронтом волны понимается геометрическое место точек, до которых дошло световое возбуждение в данный момент времени.
Позднее Френель дополнил принцип Гюйгенса:
Вторичные световые волны, интерферируя между собой, взаимно гасятся во всех направлениях, кроме первоначального направления распространения волны.
Интерференция света — это явление перераспределения энергии световых волн в пространстве, при наложении двух или более волновых процессов, имеющих одинаковую частоту и постоянную во времени разность фаз.
Источники света, имеющие одинаковую частоту и постоянную во времени разность фаз, называются когерентными. Пусть имеются два когерентных источника света, в которых колебания совершаются по закону s = A sin ωt.
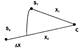
В точке С колебания, распространяющиеся от источника S1, будут совершаться по закону:
s1 = A sin (ω t - 2πx1/λ),
а от источника S2 по закону:
S2 = A sin (ωt -2πx2/λ).
Так как волны приходят в точку С одновременно, результирующее смещение будет в любой момент определяться суммой составляющих смещений: S = S1 + S2 S = A sin (ωt - 2πx1/λ ) + A sin (ωt -2πx2/λ ). Применяя формулу суммы синусов, получим:
S = 2 A cos[ π(х2 — х1) /λ] sin[ωt — π (х2+ х1)/ λ ].
В этом уравнении выражение х2 – х1 = ∆ х называют геометрической разностью хода волн - это разность расстояний, которые проходят волны до встречи в точке С. Выражение 2Acos (π∆х/λ) = А' является амплитудой результирующего колебания. Подставляя различные значения Ах в формулу А', были выявлены следующие закономерности: Если геометрическая разность хода волн равна четному числу полудлин волн, то амплитуда результирующего колебания будет наибольшей - в данной точке усиление колебаний.
X = (2kλ)/2
Если геометрическая разность хода волн равна нечетному числу полудлин волн, то амплитуда результирующих колебаний будет минимальной - ослабление колебаний.
X = (2k+1)λ/2
В формулах k - натуральный ряд чисел 0,1,2,3...
При когерентных источниках волн пространство, окружающее источники, будет представляться в виде совокупности максимумов и минимумов. Такое расположение называется устойчивой интерференционной картиной.Поскольку свет представляет собой электромагнитные волны, должна наблюдаться интерференция света. Однако в результате того, что отдельные световые импульсы, посылаемые высвечивающимися атомами источника света, не согласованы между собой по фазе, а кроме того, могут отличаться по частоте, картина взаимного усиления, возникающая в каком-либо участке пространства, уже через доли секунды сменяется картиной взаимного ослабления и наоборот. Хаотическая смена таких мгновенных картин глазом не воспринимается, а создает ощущение ровного потока света, не изменяющегося во времени.
Для наблюдения устойчивой во времени интерференционной картины необходимы условия, при которых частоты и разности фаз интерферирующих лучей были бы постоянными в течение всего времени наблюдения. В природе не существует когерентных источников света. Для того чтобы два светящихся тела являлись когерентными источниками, волны, излучаемые всеми частицами первого тела, должны отличаться по фазе от волн, излучаемых всеми частицами второго тела, все время на одну и туже величину. Такое событие практически совершенно невероятно. Поэтому, для получения когерентных источников прибегают к искусственному приему: "раздваивают" свет, исходящий от одного источника (зеркала или бипризма Френеля, зеркало Лойда, билинза Билле и др.). Пожалуй, единственным макроисточником света, в котором частота и фазы колебаний со временем не меняются, является лазер.
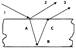
В естественных условиях образование когерентных волн и явление интерференции можно наблюдать при попадании света на тонкую прозрачную пластинку или пленку. Пучок света попадает на тонкую пластинку. Луч 1 из этого пучка попадает на точку А, частично отражается (луч 2), частично преломляется (луч АВ). Преломленный луч испытывает отражение на нижней границе пластинки в точке В. Отраженный луч, преломившись в точке С, выходит в первую среду (луч 3). Лучи 2 и 3 образованны от одного луча, поэтому они когерентны и будут интерферировать, создавая устойчивую интерференционную картину.
При освещении этой пластинки или пленки белым светом возникает весьма причудливая по форме и расцветке интерференционная картина. Такую картину дают мыльные пленки, нефтяные и масляные пятна на поверхности воды, крылья мелких насекомых, жировые налеты на стекле и другие тонкие пленки толщиной порядка 10-4см. Это интерференционное явление широко используется в оптической промышленности для так называемого просветления оптики. Дело в том, что в сложных оптических системах (фотообъективах и т.п.) значительная часть световой энергии отражается от поверхности линз. Это заметно снижает яркость и контрастность изображения и создает блики. Если на поверхность линз нанести прозрачную пленку толщиной "к/4п, изготовленную из вещества с показателем преломления п, немного меньшим показателя стекла линз, то такая пленка не будет отражать света; благодаря этому качество изображения заметно улучшится (оптика просветлеет). Кроме того, интерференцию света используют в специальных приборах — интерферометрах — для измерения с высокой степенью точности длин волн, небольших расстояний, показателей преломления веществ и определения качества оптических поверхностей.
Дифракция — явление отклонения света от прямолинейного распространения и захождение в область геометрической тени.
Вторичные волны, интерферируя, образуют на экране дифракционные максимумы и минимумы. От одной щели свет дает дифракционную картину малой интенсивности, поэтому… Дифракционная решетка — это совокупность многих параллельных щелей, разделенных непрозрачными промежутками. Общая…D sinα)/k
Разрешающая способность оптических систем
Тогда Fo6= I/ D = R / (n - 1); Го6= ∆ (n - 1) / R
Анализируя эту формулу, кажется, что, уменьшая радиус фронтальной линзы (R0O), можно получить сколь угодно большое увеличение объектива микроскопа. Однако в действительности, уменьшение радиуса фронтальной линзы, позволяет рассматривать предметы величиной, не меньше некоторого предела, который называют пределом разрешения микроскопа.
Предел разрешения микроскопа (Z) - это наименьшее расстояние между двумя точками объекта, которые еще видны в микроскопе раздельно. Величина, обратная пределу разрешения, называется разрешающей способностью микроскопа.
Разрешающая способность микроскопа - это его возможность давать раздельное изображение двух близко расположенных точек объекта.
Чтобы определить величину предела разрешения, выясним механизм получения изображения в объективе.
В качестве объекта возьмем дифракционную решетку. Рассматривание мелких предметов в микроскопе в проходящем свете, можно уподобить прохождению света через дифракционную решетку. Самой мелкой деталью дифракционной решетки является ее период (d). Свет, проходя решетку, создает картину дифракционных максимумов и минимумов в фокальной плоскости фронтальной линзы, что и является первичным изображением. После этого, лучи интерферируют, создавая в плоскости экрана вторичную картину, т.е. изображение дифракционной решетки.
Немецкий ученый-физик Эрнест Аббе - профессор теоретической физики Иенского университета в 1872 году дал теорию образования изображения в микроскопе. Он установил: Предельным условием получения изображения является то, чтобы в его построении участвовали нулевой и два первых максимума, если свет падает перпендикулярно на предмет, или нулевой и один из первых максимумов, если свет падает под углом.
При дальнейшем увеличении числа дифракционных максимумов, будет улучшаться только четкость и яркость изображения. Чем меньше предмет или его деталь (d), тем больше углы дифракции и тем шире должно быть отверстие объектива. Отверстие объектива определяется углом между лучами, приходящими от предмета к краям фронтальной линзы. Он называется отверстным углом 2U. Половина этого угла называется апертурой U. Если апертура меньше угла дифракции, соответствующего максимумам первого порядка, то изображения предмета не будет, хотя экран станет равномерно освещен лучами нулевого дифракционного максимума. Таким образом, радиус кривизны фронтальной линзы можно увеличивать до тех пор, пока апертура объектива не станет меньше угла дифракции лучей, дающих максимумы первого порядка. Тогда: k = 1, a ~ U, sin U = λ/ d, dmin ≤ λ/ sin U, dmin = Z
Z = λ/sinU
Чем меньше предел разрешения, тем более мелкие детали объекта можно рассматривать в микроскоп, т.е. тем больше будет его разрешающая способность.
Способы уменьшения предела разрешения
2. Введение иммерсионной среды.Иммерсией называется жидкость, вводимая между объектом и объективом микроскопа, которая имеет показатель преломления, близкий к показателю преломления вещества, из которого изготовлена линза.
В качестве иммерсии используют воду (n =1,33), касторовое масло (n =1,5). При введении иммерсии, свет от объектива до предмета проходит в оптически однородной среде. Это позволяет увеличить яркость изображения и уменьшить угол дифракции для лучей, образующих максимумы первого порядка.
Z = λ/ (n sinU),
где n — показатель преломления иммерсии.
3. При рассматривании объекта в наклонных лучах, величина предела разрешения определяется как:
Z = λ/ (2n sinU)
Эта формула определяет возможности оптического микроскопа давать максимальное увеличение, не искажая его форму.
Электронный микроскоп
eU = (mυ2)/2, откуда υ =((2eU)/m)1/2 По формуле Луи де Бройля λ = y/(mυ) λ = h/(m(2eU)/m)1/2, λ = h/ (2emU)1/2Поляризация света
величина магнитной индукции В, направление распространения света ОХ перпендикулярны друг другу. В источнике света излучение его отдельными атомами…Свет, колебания электрической составляющей в котором происходит в определенной плоскости, называется плоско поляризованным.
Плоскость электрической составляющей называется плоскостью колебания поляризованного луча, а плоскость магнитной составляющей, перпендикулярная ей, называется плоскостью поляризации.
Поляризацией света называется выделение из пучка естественного света лучей, колебания светового вектора которых лежат в одной плоскости.
Поляризацию можно наблюдать при отражении и преломлении света, а также при прохождении его через анизотропные среды.
Отраженный луч будет полностью поляризован, если тангенс угла падения будет равен относительному показателю преломления среды, от границы которой происходит отражение (закон Брюстера).
Tg = n
Устройства, служащие для получения поляризованного света, называют поляризаторами, а устройства, позволяющие определить положение в пространстве плоскости колебаний поляризованного света, называются анализаторами. Поляризацию света можно получить при прохождении естественного света через кристалл исландского шпата. При падении естественного света на такой кристалл, имеет место явление двойного лучепреломления, которое заключается в разделении света на два световых пучка, идущих по несколько отличным направлениям. Один из них называется обыкновенным, а другой -необыкновенным.
Кристалл исландского шпата представляет собой прозрачный ромбоэдр, все плоскости которого параллелограммы с тупыми углами 102° и острыми -78°. В кристалле имеются две вершины, в которой сходятся три тупых угла.

Прямая, соединяющая эти вершины, называется кристаллографической осью, а любая прямая параллельная ей, называется оптической осью кристалла. В направлении оптической оси двойного лучепреломления не наблюдается. Плоскость, проведенная через падающий луч и оптическую ось, называется главным сечением кристалла.
Свойства обыкновенного и необыкновенного лучей
2. Для него показатель преломления есть величина постоянная(nо=1,48). 3. Показатель преломления необыкновенного луча меняется в зависимости от его… 4. Обыкновенный и необыкновенный лучи поляризованы во взаимно перпендикулярных плоскостях.Способы получения поляризованного света.
Она изготовлена из кристалла исландского шпата. Распил делается по плоскости, соединяющей тупые углы и склеивается…МЕХАНИЗМ ОПТИЧЕСКОГО ИЗЛУЧЕНИЯ. ОПТИЧЕСКИЕ КВАНТОВЫЕ ГЕНЕРАТОРЫ
Атом и атомные системы могут длительно пребывать только в некоторых дозволенных стационарных состояниях. Этим состояниям соответствуют дискретные значения энергии. Находясь в этих состояниях, атом не излучает и не поглощает энергию.
Любое изменение энергии атома или атомной системы связано со скачкообразным переходом ее из одного стационарного состояния в другое. При этом излучается или поглощается квант энергии, равный разности дозволенных значений энергии стационарных состояний.
Н. Бор рассчитал дозволенные состояния и дозволенные энергии квантов, излучаемых атомом водорода. Эти расчеты полностью совпадали с экспериментальными исследованиями Ридберга, проведенными ранее. Однако для других атомов подобные расчеты не совпадали с экспериментальными данными. Нужны были новые не классические подходы. Поэтому, в начале 20-х годов нашего столетия начала развиваться новая наука - квантовая механика, положения которой объясняли энергетические состояния атомов и атомных систем и их поведение при излучении и поглощении энергии. Любая движущая микрочастица (в том числе и электрон в атоме) сопоставляется с волновым процессом (по де Бройлю). Положение этой частицы описывается в общем виде волновой функцией, зависящей от координат и времени - ψ (х, у, г, t). Если силовое поле, действующее на электрон стационарно (не зависит от времени), то волновую функцию можно представить произведением ψ (х, у, z, t) = F(t)ψ(x, у, z) Функция ψ(х, у, z) является вероятностной характеристикой. Выделим в пространстве объем dV = dx dy dz. В пределах dV функция ψ(x, у, z) постоянна. Вероятность нахождения частицы в объеме dV равна
DW =|ψ|2dV, откуда |ψ | 2 = dW/dV
Последнее выражение определяет физический смысл волновой функции:
Квадрат модуля волновой функции равен плотности вероятности, т.е. отношению вероятности нахождения частицы в объеме к этому объему.
Мы не будем рассматривать их подробно, они Вам хорошо известны из школьной программы и курса лекций по химии, поэтому определимся, что: 1. В атоме существуют электронные оболочки, которые обозначаются К, L, M, N,… 2. В каждой оболочке существуют подоболочки s, p, d, f, g, h, им соответствуют побочные квантовые числа 1 = 0, 1, 2,…Eмол = Eэл + Eкол + Eвр
При переходе с более высоких энергетических уровней на нижние, энергия излучается, при обратном переходе - поглощается. Энергия фотона равна разности дозволенных энергетических состояний атома или молекулы
hv = Е2- Е1
Однако не все переходы могут осуществляться, для каждого атома существуют правила отбора: одни переходы возможны или вероятны; другие переходы маловероятны, но возможны; третьи переходы вообще невозможны (запрещены). Излучаемая атомами или молекулами энергия составляет спектр испускания, поглощаемая - спектр поглощения. Получают спектры с помощью спектроскопов (дисперсионных и дифракционных). В атомных спектрах число дозволенных переходов невелико, поэтому визуально спектр состоит из отдельных узких полос и называется линейчатым. Его дают газы и пары металлов.
В молекулярных спектрах, в отдельных диапазонах частот число дозволенных переходов значительно увеличивается. Такие спектры представляют собой широкие полосы и называются полосатыми. Твердые, жидкие тела и газы под очень высоким давлением дают сплошной спектр.
Спектры являются источником различной информации:
1. По виду спектра можно судить о состоянии вещества, его температуре, давлении и т.д.
2. По спектру можно определить строение атома, молекулы, структуру их энергетических уровней.
3. По интенсивности спектральных линий определяют количество излучающих (поглощающих) атомов — количественный химический анализ (до нескольких десятков микрограмм - 109 кг).
4. По виду спектра можно определить химический состав образцов (качественный химический анализ).
Рассматривая перспективы развития отдельных разделов физики, следует обратить внимание на квантовую электронику. Она изучает методы усиления и генерации электромагнитных колебаний с использованием внутреннего излучения квантовых систем (молекул, атомов). Различают два вида квантовых излучений. Если возбужденная частица самопроизвольно переходит на более низкий дозволенный энергетический уровень, то такое излучение называют спонтанным. Оно является случайным, хаотичным во времени, частицы находятся в возбужденном состоянии 10-8 с.
Метастабильными уровнями называются уровни, где спонтанный переход маловероятен (атом находится в возбужденном состоянии 10"3с). Атомы легко переходят в невозбужденное состояние, если взаимодействуют с фотонами, энергия которых равна разности дозволенных энергетических состояний возбужденной и невозбужденной частицы. Такое излучение называют вынужденным или индуцированным. При индуцированном излучении возникают два фотона одинаковой частоты и фазы, распространяющиеся в одном направлении. Эти фотоны могут вызвать новые вынужденные переходы в других атомах и количество квантов должно было бы возрастать. Распределение частиц по энергетическим уровням описывается законом Больцмана.

Из графика видно, что наибольшее число частиц находится в невозбужденном состоянии, т.е. больше фотонов поглощается. В такой среде усиления не происходит. Усиление электромагнитных волн можно вызвать, создав активную среду, в которой хотя бы для двух уровней было распределение частиц обратное больцмановскому - так называемую инверсную заселенность. Это условие создается в квантовых генераторах. Советские ученые Н.Г. Басов, A.M. Прохоров, Ч. Американец Таунс в 1955 году сконструировали независимо друг от друга первый молекулярный квантовый генератор (мазер). В 1960 году были созданы рубиновый и гелий-неоновый квантовые генераторы — лазеры. Гелий-неоновый лазер представляет собой газоразрядную трубку из кварцевого стекла диаметром около 7 мм. В ней находится смесь неона и гелия (в соотношении 1:10) при давлении 1 мм. рт. ст. В трубку вмонтированы два электрода и два плоских зеркала, одно из которых полупрозрачное. В атоме неона реализуется Больцмановское заселение энергетических уровней. Для получения инверсной заселенности используются атомы гелия. Возбужденный уровень гелия совпадает с 3-м невозбужденным метастабильным уравнением неона. Возбуждение атома гелия осуществляется электрическим разрядом между электродами. При соударении возбужденного атома гелия с невозбужденным атомом неона происходит безизлучательная передача энергии последнему. Электрон в атоме неона переходит с 1 на 3 уровень. Для разгрузки второго уровня диаметр трубки подбирают таким образом, чтобы атомы неона, ударяясь о стенку, безизлучательно отдавали энергию и электроны переходили со 2-го на 1-й энергетический уровень. Таким образом добиваются инверсной заселенности 2 и 3 уровня неона. Фотоны, возникающие при вынужденном излучении, сами вызывают вынужденные переходы. При этом пучок фотонов, перпендикулярный зеркалам, будет испытывать наибольшее усиление (многократно отражаясь от зеркал) и выходить наружу через полупрозрачное зеркало. Уровни 2 и 3 имеют множество подуровней, поэтому гелий-неоновые лазеры могут работать на 30 длинах волн. Для получения монохроматического индуцированного излучения зеркала 1 и 2 делают с многослойными покрытиями. За счет интерференции создаются условия для усиления только одной заданной длины волны.
Свойства лазерного излучения - монохроматичность, большая мощность, узкий пучок, когерентность. Это позволяет использовать лазеры в медицине и других областях для следующих целей:
1. Измерение больших расстояний с высокой точностью;
2. В голографии;
3. Как средство связи;
4. Для сварки и резки различных материалов;
5. Применение в медицине:
При появлении лазеров, в связи с широкими перспективами их использования перед современной медициной встал ряд совершенно новых задач.
1. Всестороннее изучение влияния лазерного излучения на различные клетки, ткани, органы, системы человеческого организма в целом.
2. Изучение возможности применения лазера с лечебными целями в медицинских специальностях.
3. Разработка профилактических и лечебных мероприятий против возможного вредного действия лучей лазеров на организм человека. Вопрос о механизме действия лазеров на биологические объекты еще далеки от своего решения, в нем слишком много неясного.
Факторы действия:
1. Температурный (температура самого луча и температура ткани за счет поглощения энергии излучения).
2. Механическое воздействие лазерного излучения (ультразвуковые волны, ударные волны).
3. Ядовитые вещества, образуемые в ткани в результате действия лазерного излучения.
Эффект биологического действия лучей лазера зависит:
1.От особенностей самого излучения (тип лазера, энергия, плотность энергии, длительность и частота импульсов).
2.От физико-химических и биологических особенностей облучаемых тканей и органов (степень пигментации, кровоснабжение, теплопроводность и т.д.).
Применение в медицине:
1. Офтальмология - отслойка сетчатки, диагностика глаукомы, катаракты.
2. В терапии - консервативное лечение язв желудка, двенадцатиперстной кишки и др.
3. В хирургии:
а) при резекции печени и селезенки
б) при остановке кровотечения
в) при удалении полипов
г) при резке и сварке тканей
4. В гинекологии:
а) при лечении предраковых заболеваний влагалища, шейки матки,
б) при пластических операциях на маточных трубах, у женщин, страдающих бесплодием,
в) при удалении различных опухолей в половых органах.
5. В пластической хирургии и косметологии - для удаления кожных опухолей, татуировок, дефектов лица и головы.
6. После лазерного разреза отек и воспаление тканей невелики, что дает возможность использования его в урологии при операциях на мочеточниках, мочевом пузыре, предстательной железе и уретре.
7. Отоларингология - при удалении полипов, сосудистых опухолей носа, новообразований глотки.
8. Нейрохирургия - при операциях на головном мозге, микрохирургия (сшивание мелких сосудов, нервов, сухожилий).
РЕНТГЕНОВСКОЕ ИЗЛУЧЕНИЕ
1.Они обладают сильной проникающей способностью, которая зависит от природы вещества и толщины его. Благодаря этому свойству они получили… 2.Вызывают свечение (люминесценцию) некоторых тел. С помощью экранов из… 3.Оказывают действие на фотопленку (фотохимическое действие).Интенсивность - это величина энергии, которую несут рентгеновские лучи, через площадку 1 см2 за 1 с.
Двигающийся направленно электрон можно представить электрическим током. Попадая в электрическое поле атома, движение…Hv =(mυ12)/2 – (mυ22)/2
Минимальная энергия кванта определяется из этого уравнения,
если (mυ22)/2= 0, тогда или hvmin =(mυ12)/2
hc/λmax =eU, откуда λmax = (hc)/(eU)
Электрон, взаимодействуя с атомом анода, может удалить орбитальный электрон с ближайшей к ядру орбиты К, L, М на более отдаленную или вообще за пределы атома. На освободившееся место перейдет электрон с более удаленной орбиты. При этом излучается квант рентгеновского излучения, длина волны которого определяется разностью дозволенных энергетических состояний атома (hv = E2- E1). Следовательно, излучение может быть только определенных длин волн, спектр такого излучения будет линейчатым, а излучение называют характеристическим.

При бомбардировке вещества анода электронами существуют оба вида излучения. Рассмотрим схему рентгеновского аппарата.
В состав рентгеновского аппарата входят следующие узлы:
1. Рентгеновская трубка (РТ)
2. Повышающий трансформатор (ТР2).
3. Понижающий трансформатор (ТР,).
4. Автотрансформатор (АТР).
5. Высоковольтный выпрямитель (В).

Первичная обмотка повышающего трансформатора питается от сети переменного тока через автотрансформатор. Автотрансформатор служит для регулировки напряжения между анодом и катодом. Изменение напряжения изменяет длину волны λmin=l,24/ U, а длина волны характеризует жесткость излучения, т.о. автотрансформатор служит для регулировки жесткости рентгеновского излучения. Напряжение между анодом и катодом рентгеновской трубки в медицинских рентгеновских аппаратах до 60 кВ, в промышленных - 200 - 250 кВ. Питается трубка постоянным током. В качестве выпрямителя используются высоковольтные диоды или кенотроны, используются однополупериодные и двухполупериодные схемы. Для питания накала трубки служит понижающий трансформатор ТР1. В первичную цепь этого трансформатора ставится реостат R. Изменяя сопротивление, мы изменяем ток накала катода, а, следовательно, его температуру и число испускаемых электронов. Число электронов характеризует интенсивность рентгеновского излучения, т.о. реостат R служит для изменения интенсивности излучения, которая определяется следующей формулой:
Ф = kJU2Z',
где J - анодный ток, U - напряжение между катодом и анодом трубки, Z - порядковый номер вещества зеркальца анода. Защита от воздействия рентгеновского излучения, даваемого лечебными и диагностическими аппаратами, сводится к следующему:
1.Экранизация источника излучения. Рентгеновская трубка самозащитная. Камера закрывается свинцовыми листами.
2.Индивидуальная защита обслуживающего персонала (фартук, перчатки, стекло экрана делается из просвинцованного материала).
3. Охраняются законом (меньший рабочий день, дополнительный отпуск, спецпитание и др.)
При взаимодействии рентгеновских лучей с веществом, часть их отражается от поверхности, часть проходит через вещество без взаимодействия, часть проходит вовнутрь вещества, взаимодействуя с атомами.
При этом могут возникнуть три случая взаимодействия.
2. Если энергия кванта равна или незначительно превышает работу выхода…Hv1 = Aвых + (mυ2)/2
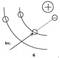
Если энергия меньше работы выхода, но достаточна для того, чтобы перевести электрон с одной орбиты на другую (с более высоким энергетическим уровнем), то может произойти излучение в видимой части спектра, рентгенолюминесценцияили активация молекул. Оба вида взаимодействия объединены общим названием - истинное поглощение.
3. Если энергия фотона значительно превышает работу по выходу электрона, что более характерно для жесткого коротковолнового излучения и внешних электронов атома, то при взаимодействии фотон отдает часть энергии. Возникает фотон с меньшей энергией и фотоэлектрон отдачи. Это явление называется не когерентным рассеянием или комптон-эффектом.

Возникающие новый фотон и электрон называют вторичным излучением. Вторичное излучение может вызывать новые реакции (когерентное рассеяние, истинное поглощение, комптон-эффект) с образованием третичных электронов, квантов и т.д. В результате всех этих процессов возникает ионизация вещества и излучение с большей длиной волны, которое рассеивается по всем направлениям.
Параллельный поток рентгеновских лучей при прохождении через вещество ослабляется. Ослабление подчиняется закону Бугера: Ф = Ф0e-μd
Фо - поток, падающий на вещество, Ф - поток, прошедший через вещество, μ - линейный коэффициент ослабления, d - толщина слоя вещества.
Для рентгеновского излучения применяемого в медицине с энергией фотонов 150-200 кэВ при глубокой терапии; 60-100 кэВ при диагностике; коэффициент ослабления определяется по формуле:
μ = kpZ3λ3,
k - коэффициент пропорциональности, зависящий от выбора единиц измерения, р - плотность вещества, Z - порядковый номер элемента, λ - длина волны излучения.
Если на пути рентгеновского излучения поместить неоднородное вещество, то на флюоресцирующем экране получим тени отдельных деталей
вещества. Таким неоднородным веществом является организм человека. Просвечивая его рентгеновскими лучами, по форме и размерам, а так же по интенсивности теневого изображения, судят о нормальном или патологическом состоянии органов. Такой метод диагностики заболеваний носит название рентгенодиагностики.Существует два основных метода рентгенодиагностики: рентгеноскопия и рентгенография. При рентгеноскопии теневое изображение органов наблюдается на люминесцентном экране. На экране более плотные ткани (сердце, кровеносные сосуды) видны темными, мало поглощающие ткани (легочные поля) - светлыми.При рентгенографии теневое изображение фотографируют на фотопленку. Изображение получают негативное (обратное) по отношению к изображению на экране.
Кроме основных методов, используются специальные приемы рентгенодиагностики.
1. Контрастная рентгенография. Для получения более контрастного изображения используются особые вещества, вводимые в ткани - отрицательные контрастные вещества (воздух, кислород) используются в плотных тканях (головной мозг), положительные контрастные вещества (соли бария, коллоиды на основе йода) для мало поглощающих тканей.
2. Флюорография.Фотографирование рентгеновского изображения с экрана на пленку небольшого формата. Экран, оптика и пленка с фотокамерой объединяются в большую светонепроницаемую систему, что позволяет делать съемку в незатемненном помещении. Этот метод применяется для массового обследования населения.
3. Электрорентгенографияотличается от обычной рентгенографии способом получения изображения; при этом методе пучок рентгеновских лучей, прошедших через тело пациента, направляется на предварительно зараженную селеновую пластину. Прошедшие через организм рентгеновские лучи, изменяют потенциал пластины на разных ее участках, соответственно интенсивности попадающего на эти участки излучения - на пластинке возникает «скрытое электрическое изображение». Для «проявления» изображения селеновую пластинку напыляют графитовым порошком, который притягивается к тем местам, где сохранился заряд и не задерживается в тех местах, которые потеряли заряд под действием рентгеновских лучей. Это изображение легко переносится на обычную бумагу. После стирания порошка пластину можно использовать вновь. На одной пластине можно провести более 1000 снимков. Главные достоинства электрорентгенографии состоит в том, что она позволяет быстро получить снимки без затрат фотопленки, без мокрого фотопроцесса, без затемнения и обладает более высокой разрешающей способностью.
4. Рентгеновская компьютерная томография. Этот метод заключается в перемещении рентгеновской трубки по определенной траектории, для фотографирования объекта с различных положений. При этом на фотопленке изображение также перемещается. Однако съемка производится таким образом, что рентгеновский луч всегда проходит одну и ту же точку О. Если перемещать эту точку, то на снимке можно получить послойное теневое изображение (томография - послойная запись). Чтение таких изображений довольно сложное. Помогает врачу в этом вопросе вычислительная техника, поэтому добавляется слово компьютерная томография. Рентгеновская компьютерная томография позволяет получать изображение с деталями около 1 мм, различаются по контрастности два образования с разностью в поглощении около 0,1 %.
5. Рентгенотелевидение. С помощью специальных фотоусилителей рентгеновского изображения (УРИ) регистрируют и усиливают слабое изображение на экране и, используя передающую телевизионную аппаратуру, получают изображение на экране телевизора. Изображение на экране телевизора значительной яркости, обеспечивает выявление сравнительно малых деталей объекта, позволяет производить фото - и киносъемку.
Рентгеновские лучи используют для «лечения» злокачественных новообразований - рентгенотерапия. При облучении живых тканей рентгеновскими лучами изменяется функциональное состояние клеток. Первичный эффект воздействия рентгеновских лучей на вещество - ионизация. Выявлено, что при летальных дозах в клетке образуется около 1 млн. ионов (всего в клетке 1014 атомов). При первичном размене энергии никаких видимых структурных изменений в атомах и молекулах не происходит. Современная физиология рассматривает первичные эффекты взаимодействия ионизирующего излучения с веществом (в том числе и рентгеновского) в двух аспектах: взаимодействие с молекулами воды в водных растворах и действие на органические соединения. В водных растворах образуются радикалы (ОН-, Н+), гидроперекисные и перекисные соединения (Н2О2), обладающие большой химической активностью. При воздействии на органические соединения образуются возбужденные молекулы, радикалы, ионы, перекиси, которые так же в химическом отношении весьма активны. Т.о. первичное взаимодействие происходит по физическим законам возбуждения и ионизации молекул. Ионизация атомов и молекул вызывает вторичные процессы, развивающиеся по биологическим законам. Активные перекисные соединения окисляют и изменяют клеточные ферменты, что вызывает нарушение нормального протекания биохимических процессов - клетки теряют способность синтезировать определенные типы белков, без которых невозможно деление клетки. Возникают мутации, изменяется течение белкового, углеводного, пептидного и холестеринового обмена веществ. При таких реакциях белковые молекулы могут разрушаться и распадаться на аминокислоты, вплоть до образования весьма токсичных гистаминоподобных соединений, под влиянием которых развиваются дистрофические и некротические изменения. Особенно сильно рентгеновские лучи действуют на быстрорастущие, малодифференцированные клетки - кроветворные органы, кожу, гонады, что позволяет использовать рентгеновские лучи для облучения раковых опухолей этих образований. Следует помнить, что излучение действует не только на биологический объект, подвергнутый облучению, но и на последующие поколения, через наследственный аппарат клеток.
ЯДРО АТОМА. РАДИОАКТИВНОСТЬ
Массовое число - это целое число, ближайшее к атомной массе элемента, выраженной в а.е.м.
Основные свойства ядерных сил: 1. Ядерные силы - короткодействующие. Радиус действия 1013 см. При увеличении… 2. Ядерные силы - сильнодействующие. Они на несколько порядков выше, чем силы любых других известных в природе…Радиоактивность — свойство ядер определенных элементов самопроизвольно превращаться в ядра других элементов с испусканием особого рода излучения, называемого радиоактивным излучением.
Радиоактивные явления, происходящие у встречающихся в природе радионуклидов, называются естественной радиоактивностью, а происходящие в искусственно полученных радионуклидах - искусственной радиоактивностью. Оба вида радиоактивности подчиняются одним и тем же законам.
Радиоактивное излучение сложное по составу. Различают шесть видов: α, β, γ - излучения, спонтанное деление, протонная и двух протонная радиоактивность.
Все радиоактивные излучения:
1. Обладают фотохимическим действием.
2. Вызывают ионизацию газов и веществ, через которые проходят.
3. Вызывают свечение (флюоресценцию) ряда твердых тел и жидкостей.
4. Радиоактивные излучения сопровождаются выделением энергии.
Удельная ионизация характеризуется количеством пар ионов, образующихся на 1 см пробега частицы в воздухе.
Альфа-излучение состоит в самопроизвольном превращении ядра с испусканием α-частицы. Схема этого распада с учетом…Распределение испускаемых частиц по энергиям называется спектром радиоактивного излучения.
Альфа частицы, испускаемые определенным элементом, составляют несколько групп1 с близкой энергией, поэтому спектр состоит из нескольких близко расположенных линий.
Бета-распад заключается во внутриядерном взаимном превращении нейтрона и протона.
Различают три вида β - распада.
1. Электронный распад проявляется в вылете из ядра электрона. Энергии β -частиц принимают всевозможные значения, поэтому спектр энергий - сплошной.
2. Схема β- - распада с учетом правила смещения:
ZXA → Z+1Y A + -1 β 0 + v,
где - антинейтрино. Примером β- - распада может быть превращение трития в гелий.
H3 → 2He3 + -1e0 + v
При β- - распаде электрон образуется вследствие внутриядерного превращения нейтрона в протон:
N1 → 1p1 + -1e0 + v
4. Электронный, или е-захват. Этот вид радиоактивности заключается в захвате ядром одного из внутренних электронов атома, при этом протон ядра… Схема электронного захвата: zXA+ -1β° → z-1YA + v Ядро, образовавшееся в результате α и β -распада, находится обычно в возбужденном состоянии, поэтому, как…Коэффициентом размножения нейтронов К называется от ношение числа нейтронов, возникающих в некотором звене реакции, к числу таких нейтронов в предыдущем звене.
Если k ≥ 1, то происходит цепная реакция.
Практическое применение этого вида радиоактивности - атомная энергетика, атомная и нейтронная бомба.
В 1934 г. Французские ученые Ирен и Фредерик Жолио-Кюри открыли явление искусственной радиоактивности. Оно состоит в том, что при некоторых ядерных реакциях, осуществляемых с помощью элементарных частиц (а-частиц, нейтронов и др.), могут возникать искусственно радиоактивные ядра, дающие собственные радиоактивные излучения.
Радиоактивный распад - статистический процесс. Нельзя указать заранее момент распада ядра, но можно установить вероятность этого распада. Эта вероятность характеризуется коэффициентом распада X, который называется постоянной распада и зависит только от природы элемента. Процесс распада подчиняется основному закону радиоактивного распада: За равные промежутки времени распадается одинаковая доля наличных (т.е. не распавшихся к началу данного промежутка времени) ядер данного элемента.
Пусть за достаточно малый интервал времени dt распадается dN ядер. Оно будет пропорционально этому интервалу времени и общему числу N радиоактивных ядер: dN = -λNodt
Пусть при t = 0, N = No (начальное число ядер). Решая дифференциальное уравнение, получим:
DN)/N0 = -λdt
DN)/N0 = -λ ∫dt
InN│ = -λt│
InN – InN0 = -λt
InN/N0 = -λt, потенцируем, тогда N/N0 =e-λt
N = N0e-λt
На практике чаще используют другую характеристику - период полураспада Т.
Период полураспада - это время, в течение которого распадается половина исходных радиоактивных ядер.
Исходя из этого:
N0/2 = N0e-λT
1/2 = e-λT
In2 = λT
T = In2/λ = 0.693/λ
При использовании радиоактивных источников важно знать число ядер, распадающихся за секунду и вылетающих из вещества.
Скорость распада называется активностью радиоактивного вещества.
A = -(dN)/dt
A = λN = 0.693N/T
A = λN0e-λt
Она является существенной характеристикой радиоактивного источника. Таким образом, активность тем больше, чем больше радиоактивных ядер и чем меньше их период полураспада. Активность препарата со временем убывает по экспоненциальному закону.
Единица активности - беккерель (Бк) - за 1 с происходит один акт распада 1Бк= 1с'
Наиболее употребительной единицей активности является кюри (Ки): 1Ки= 1,7-1010Бк = 3,71010с-1 Внесистемная единица активности - резерфорд (Рд) 1Рд=106Бк=106с1
Детекторы (регистраторы) ионизирующих излучений условно можно разделить на три группы: следовые (трековые) детекторы, счетчики и интегральные приборы. К следовым относят камеру Вильсона, диффузионную, пузырьковую камеры и толстослойные фотопластинки. Общим для них является то, что наблюдаемая частица ионизирует молекулы или атомы вещества на своем пути. Образованные ионы проявляются по вторичным эффектам: конденсация перенасыщенного пара (камера Вильсона и
диффузионная); парообразование перегретой жидкости (пузырьковая камера); фотохимическое действие (толстослойные фотопластинки).
К следующей группе методов и приборов наблюдения и регистрации относятся сцинтилляционный и ионизационный счетчики. Сцинтилляционный счетчик основан на радиолюминесценции, т. е. флуоресценции вещества под действием радиоактивного излучения. Он представляет собой экран, покрытый люминофором, на котором каждый удар радиоактивной частицы вызывает свечение его (спинтарископ). Это явление можно наблюдать визуально. Более сложным и очень чувствительным сцинтилляционным счетчиком является фотоэлектронный умножитель (ФЭУ). Он представляет собой стеклянный баллон, в который впаян один катод и несколько анодов А,, А2, А3 и т. д. Вырванные фотоэлектроны под воздействием α-частицы летят к анодам и выбивают из них несколько вторичных электронов, образуя поток электронов. В результате на выходе ФЭУ возникает значительный импульс тока, регистрируемый счетным устройством. Ионизационный счетчик (счетчик Гейгера-Мюллера) основан на возникновении газового разряда при ионизации газа, движущейся радиоактивной частицей, который является главной частью радиометра. Он представляет собой стеклянный или металлизированный медью, либо металлический цилиндр, наполненный газом аргоном. По его оси натянута металлическая нить, имеющая относительно стенок трубки положительный потенциал порядка 1000 В. Попадание во внутрь цилиндра ионизирующей частицы приводит к появлению в счетчике ионов — это первичная ионизация. Эти ионы, ускоряясь полем, существующим между нитью и цилиндром, вызывают вторичную «лавинную» ионизацию, в трубке начинается разряд.
При рассмотрении вольтамперной характеристики счетчика зависимость тока, протекающего через счетчик, от приложенного напряжения - видно, что на участке графика 0-U, ток в цепи счетчика изменяется прямо пропорционально приложенному напряжению (первичная ионизация). Далее на участке (2) при повышении напряжения значения тока остаются постоянными (ток насыщения при первичной ионизации). Дальнейшее увеличение напряжения на участке графика 3 возникает вторичная ионизация газа (регулируемый разряд). На участке 4 дальнейшее увеличение напряжения вызывает самостоятельный (лавинообразный не регулируемый) разряд. Счетчик работает в режиме самостоятельного разряда (участок U3-U4). Так как в момент лавинообразной ионизации счетчик не может реагировать на новые частицы, то возникающий разряд должен быть погашен.

Простейший способ гашения лавинообразного разряда в счетчике состоит в том, что в цепь счетчика включается большое нагрузочное сопротивление RH около 108 Ом. Тогда импульс тока в трубке вызывает на этом сопротивлении большое падение напряжения, при этом напряжение на счетчике резко уменьшается – разряд гасится и счетчик готов к приему следующей ионизирующей частицы. Таким образом, за один акт попадания ионизирующей частицы в счетчик он отвечает одним импульсом тока. Самогасящиеся счетчики содержат помимо инертного газа еще многоатомные спирты (например, Аг + 10% С2Н5ОН при давлении 10 мм. рт. ст.). В таких трубках разряд прекращается вследствие поглощения энергии ионизированных молекул аргона парами спирта. В трубке возникает импульс, а разряд гасится. Такие счетчики способны считать за 1 секунду до 10000 ионизирующих частиц.
Радиометр состоит из 6 основных блоков:
1 - счетчик Гейгера-Мюллера; 2 - усилитель; 3 - блок питания; 4 - блок формирования прямоугольных импульсов; 5 - пересчетное устройство; 6 - регистратор числа импульсов.

Радиоактивные нуклиды в медицине используют в двух направлениях - диагностике и с исследовательскими целями. Другая группа методов основана на применении ионизирующего излучения для биологического действия с лечебной целью. Сюда же можно отнести бактерицидное действие излучения. Метод меченых атомов состоит в том, что в организм вводят радионуклиды и определяют их место нахождения и активность в органах и тканях. По скорости изменения концентрации радионуклидов можно делать диагностический вывод о состоянии органа или ткани. Для обнаружения распределения радионуклидов используют гамма топограф, который автоматически регистрирует распределение радиоактивного препарата. Он представляет собой сканирующий счетчик, который постепенно проходит участки над телом больного. Регистрация излучения фиксируется штриховой отметкой на бумаге. Используя изотопные индикаторы, можно проследить за обменом веществ в организме, определять общий объем жидкости в нем.
В эксперименте более детальные сведения можно поучить методом авторадиографии. На биологическую ткань наносится слой чувствительной фотоэмульсии. Радионуклиды оставляют след в соответствующем месте эмульсии, как бы фотографируя себя. Полученный «снимок» называют радиоавтографомили авторадиограммой. Радионуклиды вводят в количествах, не оказывающих вредного действия на организм.
В лечебном применении используются в основном γ - излучение (гамма-терапия), гамма-камера состоит из источника, обычно защитного контейнера, внутри которого помещен источник. Больной размещается на столе. Гамма излучение высокой энергии (порядка 1,0-1,4 Мэв) позволяет разрушать глубоко расположенные опухоли, при этом поверхностные органы и ткани подвергаются меньшему губительному действию. В настоящее время в медицинской практике применяются ускорители заряженных частиц как средство лучевой терапии для глубоко расположенных злокачественных образований.
ДОЗИМЕТРИЯ ИОНИЗИРУЮЩЕГО ИЗЛУЧЕНИЯ
Для характеристики ионизирующего излучения вводятся величины: физическая, или экспозиционная доза, доза поглощения, мощность дозы.Доза поглощения характеризует ту часть энергии ионизирующего излучения, которая поглощается при прохождении через единицу массы вещества.
Dn = En/m
В системе СИ доза поглощения измеряется в греях (Гр). Это такая доза, при которой в 1кг облучаемого вещества поглощается 1 Дж энергии излучения. Внесистемная единица измерения - 1 рад. 1 рад.= 102 Гр.
Однако практически измерять поглощённую дозу излучения довольно трудно, так как облучаемые тела неоднородны, энергия рассеивается по различным направлениям и др. Поэтому оценивать поглощенную дозу принято по ионизационному действию рентгеновского или γ - излучения на чистый сухой воздух. Такая оценка характеризуется экспозиционной или физической дозой.
Экспозиционная доза определяется зарядом ионов одного знака, образующихся в единице массы сухого воздуха под действием рентгеновского или γ - излучения.
D0 = q/m
В системе СИ измеряется - Кл/кг. Внесистемная единица один рентген (Р). Это экспозиционная доза рентгеновского или у - излучения, при которой в результате полной ионизации 0,001293 г сухого воздуха образуются ионы, несущие заряд в 1 ед. СГСЭ. 1Р = 2,58х10-4Кл/кг
При действии ионизирующего излучения на живые ткани важно знать не только величину дозы, но и время, в течение которого эта доза поглощалась. Для этого вводится понятие мощности дозы Р.
Мощность дозы определяется отношением величины дозы к промежутку времени, в течение которого излучение действовало.
Для дозы поглощения: P. = D./t
Для экспозиционной дозы: Р. = D0/t
Единицы измерения:
[P.]: СИ - Гр/с, внесистемная - рад / с;
Р0]: СИ - А/кг, внесистемная - Р / с, Р / мин, Р / час
Определено, что если поглощенная доза измеряется в радах, а экспозиционная в рентгенах, то f равно: для воздуха - 0,88, для воды и мягких тканей -… Приближенные значения К для некоторых излучений: рентгеновское или γ - излучение - 1Do = q/m = C/m (φ1 – φ2) = k(φ1 – φ2), где k = C/m
Таким образом, экспозиционная доза прямо пропорциональна разности показаний электрометра. Шкалу электрометра градуируют в единицах экспозиционной дозы: Р, мР. Зная переводной коэффициент, можно определить дозу поглощения, а измерив время излучения, определить мощность дозы.
Дозиметр, основанный на измерении тока ионизации, состоит из ионизационной камеры с двумя электродами, на которые через сопротивление R подается высокое постоянное напряжение. Величину напряжения подбирают таким образом, чтобы дозиметр работал в режиме насыщения, т.е. все образовавшиеся ионы участвовали в создании тока, но не существовало вторичной ионизации. При облучении камеры возникающие ионы (первичные) участвуют в образовании тока. Величину тока можно определить, зная падение напряжения на сопротивлении R :
J = U/R.
Из электродинамики известно, что J = q/t. Поделив обе части этого выражения наши, подставив значение тока (J = U/R), получим:
J/m = q/(mt) или U/(Rm) = D0/t
Окончательно: P0 =kU, где k = 1/(Rm)
Из последней формулы видно, что мощность экспозиционной дозы пропорциональна показаниям вольтметра, поэтому шкалу вольтметра градуируют в единицах мощности экспозиционной дозы: Р/час, Р/мин и т.д. Т.к. ток очень мал, то сопротивление R нужно взять большим, чтобы получить значительное падение напряжения (U = JR). Но измерить это напряжение можно вольтметром, у которого еще большее сопротивление, иначе оно будет шунтировать R. Таким прибором является катодный ламповый вольтметр.
В зависимости от возможных последствий влияния ионизирующих излучений на организм "Нормами радиационной безопасности" (НРБ) установлены следующие категории:
Категория А - персонал (профессиональные работники) - лица, которые постоянно или временно непосредственно работают с источниками ионизирующих излучений.
Категория Б - ограниченная часть населения - лица, которые непосредственно не работают с источниками излучений, но по условиям проживания или размещения рабочих мест, могут подвергаться воздействию радиоактивных веществ и других источников излучений, применяемых в учреждениях или удаляемых во внешнюю среду с отходами.
Категория В - все остальное население области, края, республики.
В зависимости от радиочувствительности, установлены три группы критических органов или тканей человека:
I группа - все тело, гонады и красный костный мозг.
II группа - мышцы, щитовидная железа, жировая ткань, печень, селезенка, почки, желудочно-кишечный тракт, легкие, хрусталик глаза и другие органы, за исключением тех, которые относятся к I и III группам.
III группа - кожный покров, костная ткань, кисти рук, предплечья, лодыжки и стопы.

Понятие предельно-допустимая доза (ПДД) было сформулировано как: наибольшее значение индивидуальной эквивалентной дозы за год, которое при равномерном воздействии в течение 50 лет не вызовет в состоянии здоровья персонала (категория А) неблагоприятных изменений, обнаруживаемых современными методами.
ПДД является основным дозовым пределом категории А. Для категории Б установлен предел дозы (ПД) - предельная эквивалентная доза за год. Она контролируется по установленной для критических групп органов дозе излучения, уровню радиоактивных выбросов и радиоактивного загрязнения внешней среды. ПД является основным дозовым пределом для категории Б.
МАТЕРИЯ И ДВИЖЕНИЕ. СОВРЕМЕННЫЕ ВЗГЛЯДЫ НА ПРИРОДУ ВЕЩЕСТВА И ПОЛЯ
В последнюю четверть века широкое распространение получила кварковая теория строения вещества. Сущность ее состоит в…Странность - это особое квантовое число, которое характеризует сильные и электромагнитные взаимодействия при рождении пары странных частиц. Оно может быть равно+!,-1,+2,-2, 0
Барионный заряд - это особое квантовое число, присущее только барионам.
ррр - ррη – pηη - ηηη ррλ.- рηλ - ηηλ рλλ - ηλλПоле - это особый вид материи, посредством которого осуществляется связь и взаимодействие между вещественными образованиями.
Оптика или учение о свете зародилось еще в глубокой древности и первоначально возникло как попытка ответить на…МОДЕЛИРОВАНИЕ. ВЕРОЯТНОСТНЫЕ МЕТОДЫ ДИАГНОСТИКИ
Следующий тип моделей - информационные. Совокупность биологических дисциплин до недавнего времени для описания результатов исследований, и… Моделирование состоит из следующих стадий: 1. Формирование цели моделирования.Медицинская диагностика и возможности её автоматизации
Одним из выходов является автоматизированная диагностика на базе ЭВМ, особенно: 1. При большом количестве информации; 2. При преимущественном использовании количественных данных.Вероятностные методы диагностики
P(Di/S) = (P(Di)*P(S/Di))/(P(S) Пусть оцениваются два диагноза: D1 - рак легкого, D2 - пневмония и пусть у… P(D1/S) = (P(D1)*P(S/D1))/P(S), P(D2/S) = (P(D2)*P(S/D2))/P(S)P(Di) = mi/n
m - число больных с данным заболеванием, n! - общее число обследованных больных, P(S / Di) - называется условной вероятностью данного симптомокомплекса при заболевании Di.
P(S / Di) = P(S1/D1) * P(S2/D1) * P(S3/D1) * ...
где P(S1/D1), P(S2/D1), ...- условные вероятности отдельных симптомов, по отношению к данному диагнозу и находятся в медицинской памяти, содержащейся в ЭВМ. Они могут быть определены статистически, а медицинскую память можно представить в виде матрицы.

Знаменатель формулы представляет полную вероятность наличия симптомокомплекса при всех болезнях, т.е. сумма произведений априорной вероятности каждой из болезней на условную вероятность симптомокомплекса при каждой из этих болезней
P(S) = ∑[P(Di)*P(S/Di)]
Он входит в формулу Байеса для нормировки, т.е. чтобы получающиеся вероятности были выражены в процентах. Болезнь, имеющая наибольшую вероятность, при наличии данного симптомокомплекса и будет рассматриваться как искомый диагноз.
СТРУКТУРНЫЕ ОСНОВЫ ФУНКЦИОНИРОВАНИЯ МЕМБРАН
Различного вида исследования показали, что липидный бислой может находиться в двух состояниях: 1. Твердого двухмерного кристалла 2. Бимолекулярной жидкой пленки (жидкокристаллической).C = (εε0S)/d
Толщина мембраны составляет (0,4 - 0,9) нм. Если е = 13, тогда величина этой емкости (0,5 - 1,3)10-2 нм на единичной площади. Вязкость мембраны на два порядка выше вязкости воды и составляет (30 - 100) МПа*с. Поверхностное натяжение мембраны (0,03 - 1,0) нН/м. Распределение электрического потенциала мембраны и ее границ можно считать важным фактором, определяющим скорость переноса веществ через мембрану.
Поскольку живая клетка, как термодинамическая система, обменивается с окружающей средой веществом, энергией и информацией, то транспорт веществ через мембрану является неотъемлемым свойством существования клетки. Он обеспечивает биоэнергетику клетки (синтез АТФ), формирование специальных структур внутри клетки, осуществляет действие лекарственных веществ на цитоплазму, саму мембрану, ферментативные системы и рецепторы.
Различают два вида транспорта веществ: пассивный, когда частицы переносятся по градиенту без затрат энергии, и активный, требующий затрат химической энергии, которая освобождается при гидролизе АТФ.
По пути простой диффузии в клетке обеспечивается проницаемость мембран для 02 и СО2, большинства ядов и лекарственных веществ. Это самый медленный и мало управляемый процесс. Для переноса питательных веществ и необходимых для жизнедеятельности ионов эволюция выработала специальные белковые поры (каналы). Диффузия через поры происходит при возбуждении мембраны. В этом случае в ней открываются специальные каналы, через которые по градиенту устремляются потоки веществ и ионов.
Ряд веществ служит ионофорами - переносчиками катионов. К ним относится циклический антибиотик валиномицин (подвижный переносчик). Он представляет собой нейтральную молекулу с высокой поляризуемостью, образующую с ионами К+ сферические комплексы, которые снижают барьер для прохождения иона. Присоединяя ион К+, он транспортирует его внутрь клетки. На внутренней поверхности ионы К+ высвобождаются. Переносчик возвращается к наружной поверхности мембраны. Далее цикл повторяется. Вторым переносчиком является грамицидин, который образует в мембране полярную пору. Транспорт, облегченный образованием пор, имеет эстафетный характер - пора может быть образована несколькими последовательно расположенными молекулами, между которыми происходит передача иона. Ион может переноситься не одной, а сразу несколькими молекулами ионофора - это коллективный процесс.
Пассивный транспорт описывается уравнением Нернста - Планка.
Ф = -uRT(dC/dx) – ucZF(dφ/dx)
где: Ф - поток вещества,
u - подвижность иона, молекулы,
R - универсальная газовая постоянная,
Т - температура по шкале К0,
dC/dx - концентрационный градиент,
С - концентрация в молях,
Z - величина заряда иона,
F - число Фарадея,
dφ/dx - градиент потенциала.
В этом уравнении первое слагаемое определяет поток незаряженных частиц, второе - заряженных, знак « - » показывает, что суммарная плотность потока вещества при диффузии направлена в сторону уменьшения концентрации.
Для описания диффузии незаряженных частиц используют уравнение Фика:
Ф = -D(dC/dx)
В этом виде уравнение Фика определяет поток незаряженных частиц через единичную площадь в случае, если не существует перегородки (мембраны), которая может затруднять перенос, где: D - коэффициент диффузии, dC/dx -градиент концентрации.
Для клеточной мембраны : dx = L - толщина мембраны, dC = Сi - Сe , где Сi и Сe - концентрация частиц внутри и снаружи клетки. В уравнение Фика для клетки добавляется коэффициент К (коэффициент распределения), который определяет соотношение концентрации частиц между средой и мембраной и в конечном итоге скорость переноса. Учитывая это, уравнение Фика для клеточной мембраны представляется в виде:
Ф = -((DK)/L)(Ce – Ci)
DK / L = Р - называют эффективным коэффициентом проницаемости, тогда Ф = - Р (Сe- Ci)
Мембраны обладают также селективной проницаемостью, т.е. различным коэффициентом проницаемости, который при простой диффузии определяется коэффициентом распределения К, а в случае облегченной диффузии - избирательностью канала и переносчика.
Хорошо известны четыре основные системы активного транспорта ионов в живой клетке: 1. Na+-K+, 2. Са++, 3. Н+, 4. Протонный (в дыхательной цепи митохондрий). Во всех случаях перенос ионов через мембрану производится за счет энергии гидролиза АТФ (специальными ферментами переносчиками), называемыми транспортными АТФ-азами. Мы рассмотрим только механизмы Na+-К+-АТФ-азы. Несмотря на значительные различия в структуре Na+-K+ и Са++- АТФ-аз, в механизме их осуществления много общего.
Ионы Na+ и К+ определяют водно-электролитный обмен организма. В норме в живых клетках животных существует асимметрия концентраций этих ионов внутри (i) и снаружи (е) клетки.
К+]i > [К+]e
Na+]i < [Na+]e
ФТФ + HOH → АДФ + ФН + ΔG , где Ф - неорганический фосфат. Основные этапы работы АТФ-азы: 1. Присоединение 3 ионов Na+ и фосфорилирование фермента внутри клетки.ЭЛЕКТРОГЕНЕЗ БИОПОТЕНЦИАЛОВ
1. Если рассечь живую ткань, то между поврежденным и неповрежденным участками можно зарегистрировать постоянную разность потенциалов, называемую… 2. При наложении электродов между внутренней и внешней средой клетки, на… 1). При нанесении раздражения на клетку, нервное или мышечное волокно, они переходят в возбужденное состояние.…Диффузный потенциал Δφд.
Для его возникновения необходим контакт электролитов с различной концентрацией и различной подвижностью анионов и катионов (UH+ » UCl- ). Граница… Δφд = ((U+ - U- * RT)/(U+ = U- *nF))ln C1/C2 2. Равновесный мембранный потенциал Δφм(р).Ф0 = ФK+ + ФNa+ – ФCl- = 0
Суммарный поток по их предположениям обусловлен, с одной стороны, активным транспортом ионов Na+ и К+ за счет энергии, выделяемой при гидролизе АТФ, с другой стороны, пассивным транспортом ионов Na+, K+ и С1-, так как клеточная мембрана проницаема для всех этих ионов. Указанные потоки постоянны, их величины зависят от градиента концентрации ионов по обеим сторонам мембраны и от коэффициента проницаемости через поры и каналы мембраны, согласно уравнению Фика. Возникший за счет этого на мембране потенциал, определяется уравнением Гольдмана-Ходжкина-Катца и называется стационарным:
Δφм(c) = (RT)/(nF) ln((PK+[K+]e + PNa+[Na+]e + PCl- [Cl-]i)/. (PK+[K+]i + PNa+[Na+]i + PCl- [Cl-]e))
4. Потенциал электрогенной помпы Δφэ.п. предыдущей задаче мы определяли стационарный потенциал на мембране клетки, который обусловлен суммарным потоком активного и пассивного транспорта ионов через мембрану. Однако можно рассматривать мембранный потенциал, выраженный только через характеристики активного транспорта веществ, в частности через стехиометрический коэффициент γ.
Δφэ.п. = (RT)/(nF) ln((γPK+[K+]e + PNa+[Na+]e)/. (γPK+[K+]i + PNa+[Na+]i))
Таким образом, рассмотрены 4 случая образования постоянной разности потенциалов на мембранах. Все эти случаи могут приводить к возникновению, так называемого потенциала покоя на клеточной мембране. Потенциал клеточной мембраны может меняться при действии различных естественных или искусственных раздражителей.

1. При раздражении клетки (например, прямоугольными импульсами) клеточная мембрана становится избирательно проницаемой для ионов Na+. Они начинают активно проникать внутрь клетки по градиенту, уменьшая электроотрицательный потенциал протоплазмы в конечном итоге до 0 (линия АВ).
2. Дальнейшее поступление Na+ в клетку по градиенту инверсирует потенциал клеточной мембраны (линия ВС).
3. При достижении точки С натриевые каналы мембраны закрываются, открываются калиевые каналы. К+ начинает активно выходить из клетки по градиенту, уменьшая тем самым положительный клеточный потенциал (линия CD).
4. В точке D мембрана приходит в исходное состояние по проницаемости для ионов К+ и Na+. Дальнейшее изменение потенциала (линия DE) происходит за счет действия К+ — Na+ ~~ помпы. В точке Е клетка приходит в исходное состояние — возбуждение отсутствует.
Для измерения биопотенциалов покоя и биопотенциалов действия необходима специальная аппаратура :
1. Микроэлектроды. Они изготовляются из стекла и заполняются децинормальным раствором КС1, в котором помещается проволока из хлорированного серебра. Диаметр микроэлектрода (0,1?1) микрон. Сопротивление микроэлектрода ~ 1 МОм, электроды неполяризующиеся.
2. Усилитель напряжения биопотенциалов (УУ) должен иметь очень большое входное сопротивление порядка 10 МОм.
3. В качестве устройств регистрации (УР) могут использоваться осциллоскоп или самописец.
В заключение следует отметить основные особенности формирования биопотенциалов.
1. Первичной морфофункциональной единицей, в которой возникает источник ЭДС, является клетка.
2. Биопотенциалы, создаваемые при работе органов и тканей, являются результатом геометрического суммирования полей, образуемых отдельными клетками, составляющими эти органы и ткани.
3. Биопотенциалы имеют ионную природу, их причина — асимметрия концентрации ионов по обе стороны клеточной мембраны.
4. Биопотенциалы отражают явления и процессы, протекающие в биологических объектах, и электрограммы являются одним из методов диагностики заболеваний.
АКТИВНО-ВОЗБУДИМЫЕ СРЕДЫ
При возбуждении, в результате изменения проницаемости клеточных мембран для ионов Na+ и К+, происходит вначале деполяризация, а затем реполяризация… Однако, возбуждение участка не является локальным, оно переходит на другие… Рассмотрим процесс распространения возбуждения по нервной клетке (нервному волокну).В возбужденном участке А…J = ЭДС/(R + r), а так как R<<r, то J = ЭДС/r
В зависимости от частоты, формы, амплитуды напряжения источника ЭДС меняется и ток во внешней цепи, а, следовательно, и падение напряжения на сопротивлении R. Снимаемое напряжение с удобных точек внешней цепи является ЭКГ, которая отражает электрические и физиологические процессы, происходящие при распространении возбуждения в сердце описанным выше способом. Поэтому ЭКГ и является одним из средств диагностики заболеваний сердечно-сосудистой системы.
БИОФИЗИКА МЫШЕЧНОГО СОКРАЩЕНИЯ
Скелетная мышца позвоночных состоит из нескольких тысяч параллельных мышечных волокон диаметром (1СМ-1ОО мкм), заключенных в общую оболочку.…A = FAL
Согласно первому закону термодинамики, изменение внутренней энергии ΔU мышцы будет равняться сумме выделенного тепла и совершенной работы:
U = Q + kΔL + FΔL или ΔU = Q + (k +F)ΔL
КПД = A/ΔU или КПД =(FΔL)/(Q + (k + F)ΔL
Учитывая, что величины Q и к не зависят от F, из уравнения следует, что, в определенных пределах, КПД мышечного сокращения будет увеличиваться при увеличении нагрузки. Хилл, на основании полученных им в опытах данных, определил, что КПД мышечного сокращения примерно равен 40%. Величина КПД 40% показывает эффективность превращения энергии АТФ в механическую энергию.
АКТИВНЫЕ И ПАССИВНЫЕ ЭЛЕКТРИЧЕСКИЕ СВОЙСТВА ОРГАНОВ И ТКАНЕЙ
Дипольный момент - это вектор, определяющийся произведением тока диполя (равного суммарному току во внешней среде) на вектор расстояния между полюсами диполя(L).
Направление D от отрицательного полюса диполя к положительному.
Различают диполи точечные и конечные, точечные диполи имеют |L| → 0 . Рассматривают также электрические поля, создаваемые одним полюсом диполя, их называют униполями.
Рассмотрим значение потенциала, создаваемого точечным зарядом, элементарным диполем, органом тела человека. Будем считать, что окружающая их среда однородна в электрическом отношении.
1. Потенциал униполя в любой точке определяется по формуле:
φу = (pJ)/(4 πr)
где р - удельное сопротивление среды, J - ток, исходящий из данной точки униполя, r - расстояние от заряда до данной точки.

2. Потенциал поля, созданный элементарным диполем, определяется по формуле:
G = (pJL cos α)/(4πr2) + G
В этой формуле G есть сумма членов ряда, в котором каждое слагаемое пропорционально: L2/r3, L3/r4, L4/r5,... Если r » L , то всеми членами ряда можно пренебречь и тогда
φg = (pJL cos α)/(4πr2)
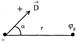
3. Электрическое поле, создаваемое каким-либо органом (например сердцем) равно геометрической сумме полей, создаваемых отдельными диполями, возникающими при работе этого органа. Потенциал поля в любой точке равен сумме потенциалов, создаваемых отдельными диполями
φ… = ∑φg = ∑((pJi Licos αi)/(4 πri2)) = p/(4 πr2)∑JiLicos απ∑α
ri = const, т.к. размеры возбужденного участка незначительны по сравнению с расстоянием r. Можно доказать, что,
∑Dicos αi = D0cosα0
где Do - суммарный дипольный момент сердца, равный геометрической сумме дипольных моментов элементарных диполей, и тогда φорг = (pD0 cos α0)/(4 πr2)

Приведенные выше количественные характеристики легли в основу одного из основных методов анализа возбудимости миокарда - многополярное отведение ЭКГ.
К пассивным электрическим свойствам биологических объектов относятся: сопротивление, электропроводимость, емкость, диэлектрическая проницаемость. В норме и патологии эти параметры меняются и поэтому могут быть использованы для изучения структуры и физико-химического состояния биологического вещества. Эти свойства проявляются, если к исследуемому участку ткани приложить напряжение небольшой величины.
При приложении постоянной разности потенциалов к тканям организма в них наблюдается два явления:
1. Постоянный электрический ток в проводящих тканях.
2. Различные виды поляризации в диэлектрических тканях. Величина тока в тканях определяется по закону Ома для участка цепи, однако для электролитов, а следовательно и биообъектов, закон имеет своеобразный вид:
J = (U – εn(t))/R
В этой формуле U - приложенное к участку ткани напряжение, R - активное сопротивление этого участка, εn (t) – ЭДС поляризации, которая возникает в результате поляризационных явлений как на электродах, так и внутри ткани на полупроницаемых и непроницаемых для ионов перегородках. ЭДС поляризации со временем возрастает, а ток в тканях уменьшается и при длительном воздействии становится равным нулю
 .
.
В диэлектриках заряды связаны, однако они перемещаются при наложении внешнего электрического поля внутри микроструктуры: атома, молекулы, клетки или в пределах границы проводящей и непроводящей среды. Для каждого вида поляризации приводится значение времени релаксации τ.
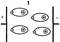

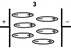
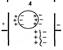


Время релаксации - это время, в течение которого поляризация увеличивается от нуля до максимума, с момента приложения внешнего напряжения.
2. При ионной поляризации происходит смещение ионов в кристаллической решетке вдоль направления электрического поля, = (10-8 - 10-3)с. 3. Дипольно-ориентационная поляризация происходит в структурах, в которых уже… 4. При микроструктурной поляризации происходит перераспределение ионов в результате действия электрического поля на…E0 /E
где Ео - напряженность внешнего электрического поля в вакууме, Е - напряженность поля в среде, оно равно разности Ео и Еn, где Еn - напряженность поля, создаваемая наведенными диполями при поляризации. Относительную диэлектрическую проницаемость можно определить также соотношением емкостей
ε = C/C0
где Со - емкость электродов в вакууме, С - емкость электродов в среде.
При приложении к биологическому объекту переменного (как правило, синусоидального) напряжения, в нем также возникают электрический ток и поляризационные явления. Электрическую модель биологического объекта для переменного тока можно представить в виде двух сопротивлений:
- активного, определяемого по формуле Ra = (pL)/S
- емкостного Rc = 1/(ωC)
- индуктивное сопротивление равно нулю.
Эти сопротивления в самой ткани могут быть соединены как последовательно так и параллельно.
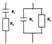 Общее сопротивление ткани в цепи переменного тока называется импедансом и обозначается Z. Импеданс определяется по формуле:
Общее сопротивление ткани в цепи переменного тока называется импедансом и обозначается Z. Импеданс определяется по формуле:
- при последовательном соединении
- при параллельном соединении:
Импеданс ткани изменяется с частотой. Это явление называют дисперсией. Величина импеданса определяется сопротивлением самой ткани, а также зависит от соотношения частоты или перио-
да приложенного напряжения и времени релаксации:
1) если Т/4 > τ (Т/4 — время возрастания приложенного напряжения от 0 до max, τ - время релаксации), проводимость объекта и диэлектрическая проницаемость с частотой не меняется,
2) если Т/4 < τ то поляризация не успевает достигнуть максимального значения , поэтому при этих условиях в некотором промежутке частот с увеличением частоты проводимость возрастает, а диэлектрическая проницаемость уменьшается,

3) если Т/4 « τ, то поляризационные явления практически не возникают, ε и p остаются неизмененными.
Пассивные электрические свойства клеток и тканей изучают с помощью мостовых схем. Метод измерения пассивных свойств тканей для диагностических целей имеет преимущество в том, что используемые напряжения не вносят существенных изменений в физико-химические процессы, происходящие в биообъекте, и тем более не повреждают его. Известно, что пассивные электрические свойства отражают изменения физиологических состояний объекта при патологии, повреждениях, действиях физических факторов (температуры, облучения, давления) и др. Рассмотрим некоторые примеры использования этого метода в биологических и медицинских исследованиях.
1. На низких частотах измерение емкости и сопротивления клеточных мембран может служить мерой их проницаемости для различного вида ионов.
2. При патологических процессах, например при воспалении, в тканях известны закономерности изменения пассивных электрических свойств. На начальной фазе воспаления происходит набухание клеток без изменения проницаемости их мембран. В это время уменьшается объем межклеточного пространства, а следовательно, увеличивается активное сопротивление ткани. В более поздние сроки воспаления происходит увеличение проницаемости клеточных мембран и, как следствие, уменьшение емкости и активного сопротивления. Таким образом, изменение электрических параметров тканей может служить средством для диагностики воспалительных процессов.
3. При действии возбуждающих факторов, а также при отмирании ткани, происходит увеличение проницаемости мембран и, как следствие, увеличения ионных потоков, т.е. ослабление эффекта поляризации границ раздела, что приводит к падению сопротивления и емкости объекта на низких частотах. На высоких частотах поляризация границ раздела практически отсутствует, поэтому высокочастотное сопротивление практически не меняется. Таким образом, степень повреждения или отмирания ткани связана с дисперсией импеданса на низких частотах, чем больше повреждение, тем меньше дисперсия.
4. В физиологии и медицине с помощью импедансометрии определяется кровенаполнение органов и тканей - при систоле сопротивление органа уменьшается, при диастоле увеличивается, т.к. кровь имеет меньшее сопротивление, чем клетки. Этот метод называется реографией. На практике исследуется кровенаполнение в печени, почках, сердце, нервной ткани, кровоток в магистральных и более мелких сосудах.
5. Одним из важных вопросов современной биофизики и электрофизиологии является содержание свободных и связанных ионов в различных образованиях биологического объекта, в частности:
- определяют концентрацию свободных ионов в цитоплазме,
- исследуют количественно процессы связывания ионов молекулами белков или других органических соединений,
- определяют степень гидратации белковых молекул,
- и другие.
В медицине с лечебной целью широко применяется нагрев высокочастотными полями и токами, причем тепловой эффект при различных методах воздействия зависит от удельного сопротивления, относительной диэлектрической проницаемости, частоты и количественной характеристики действующего фактора.
СОВРЕМЕННЫЕ МЕТОДЫ ОБРАБОТКИ ИНФОРМАЦИИ
КОЛИЧЕСТВЕННЫЕ ПОКАЗАТЕЛИ В БИОЛОГИИ И МЕДИЦИНЕ
Для измерений количественных показателей в различных областях человеческой деятельности разработан прикладной раздел науки, называемый метрологией.
Метрологией называют науку об измерениях физических величин и о способах обеспечения единства и требуемой точности этих измерений.
Измерением называют нахождение значения физической величины опытным путем с помощью технических средств. Под физической величиной следует понимать количественное значение параметров, оцениваемых физико-химических процессов, происходящих в любых реальных объектах.
Физическая величина представляет собой либо обобщенное понятие - длина, площадь, объем, доза, масса, либо конкретную величину - индивидуальную характеристику конкретного объекта или явления - длина руки, объем крови, протекающей в сосудистой системе человека, частота пульса и т.д. Технические средства для производства измерений, часто их называют просто средства измерения, могут быть самыми различными. В общем это измерительные приборы, в которых измеренная информация представляется в форме, доступной для восприятия. Наиболее распространенной формой представления информации являются цифры. В последнее время одним из распространенных средств измерения является измерительный преобразователь (датчик). Он предназначен для выработки сигнала измеренной информации в форме, удобной для передачи, дальнейшего преобразования, обработки и хранения. При измерении различных объектов, значение измеряемой физической величины отличается от истинной. Степень приближения результатов измерений к истинному значению характеризуется точностью измерений, которая является качественным показателем измерений. Количественной оценкой точности измерений является погрешность измерения - это отклонение результата измерения от истинного значения измеряемой величины. Сведения о теории погрешностей сообщаются на практических занятиях и постоянно будут использоваться в лабораторных работах при экспериментальных исследованиях. Основой для количественной оценки физической величины является единица измерения физической величины. Единицы измерения физических величин в основном группируются в системы единиц.
Под системой единиц физических величин понимают совокупность взаимосвязанных физических величин, используемых в отдельных областях естествознания.
Существуют эталонные, образцовые и рабочие средства измерения: 1) эталонные - средства измерения обеспечивают воспроизведение и хранение узаконенной… Технические устройства, используемые для измерений в медицине, принято…Рассмотрим некоторые проблемы характерные для медицинской метрологии и частично для медицинского приборостроения.
2. Время для измерения необходимо как можно меньшее, а информации и возможностей использования вычислительной техники как можно больше. 3. При медицинском нормировании важно учитывать медицинские показания и… 4. При использовании регистрирующих устройств (электрокардиограф, электроэнцефалограф) следует учитывать…ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТИ
В окружающем нас мире часто приходится сталкиваться с явлениями и фактами, которые при различных условиях могут происходить, а могут не происходить. Такие явления и факты называются случайными событиями. Понятие случайного события связано с единичными явлениями или их небольшим числом. При рассмотрении большого- числа явлений обнаруживаются определенные закономерности (рождаемость 515 мальчиков из 1000, выпадение 6 на игральной кости, вес и рост детей и т.д.).
Изучение закономерностей однородных массовых случайных явлений и составляет предмет теории вероятности и основанной на ней математической статистики.
Методы теории вероятности и математической статистики нашли широкое применение при обработке данных экспериментов в различных областях науки и техники, в том числе и медицине. Например, при оценке заболеваемости, смертности, количества несчастных случаев, в медицинской диагностике, организации здравоохранения и др.
Изучение каждого отдельного явления с выполнением некоторого определенного комплекса условий называется испытанием.
Всякий результат или исход испытания называется событием.
События принято обозначать заглавными буквами латинского алфавита А, В, С,...
Возможность появления каждого события определяется специальной величиной, вероятностью наступления события - Р(А). Есть два способа определения вероятности.
1. Пусть из N выниманий шара из урны с разноцветными шарами (с возвращением их обратно) было извлечено М белых шаров. М - называют частотой наступления событий, отношение M/N - частостью или относительной частотой. При небольшом количестве испытаний частость может принимать довольно различные значения в различных сериях опытов. При значительном числе испытаний частость принимает практически устойчивое значение.
Вероятностью случайного события называется предел, к которому стремится частость при неограниченном увеличении числа испытаний.
Р(А) = limN→∞ M/N
Это статистическое определение вероятности.
2. Поставим задачу: определить вероятность выпадения 6 при бросании игральной кости. При однократном бросании игральной кости все события (выпадение 1, 2, 3,....) являются равновозможными, единственно возможными и несовместимыми. События называются несовместимыми, если в условиях испытания каждый раз возможно появление одного из них.
Под вероятностью наступления события понимается отношение числа исходов, благоприятствующих наступлению данного события, к числу всех несовместимых, единственно возможных и равновозможных исходов испытания.
Это классическое определение вероятности. В общем виде P (A) = m/n,
где m - число благоприятствующих событий, n - число всех возможных событий при однократном испытании. В нашем примере Р(А)=1/6. Следует подчеркнуть, что 0< Р(А)<1, причем, если Р = 0, то событие невозможно, если Р = 1, то такое событие называется достоверным. Величина вероятности наступления одного из случайных событий предсказывает возможность его появления при конкретном испытании. Например, появление первого белого шара при однократном извлечении из урны с разноцветными шарами, диагноз заболевания у конкретного больного и т.д. На практике часто возникает необходимость определения вероятности наступления двух или более несовместимых событий; не важно какого, при однократном испытании. Например, выпадение на верхней грани игральной кости четного чирла. Ответ на этот вопрос дает теорема сложения вероятностей.
Вероятность появления одного (безразлично какого) события из нескольких несовместимых событий равна сумме вероятностей этих событий
Р (А или В или С...) = Р (А) + Р (В) + Р (С) + ...
В приведенном примере вероятность выпадения четного числа на верхней грани игральной кости
Р (2 или 4 или 6) = Р (2) + Р (4) + Р (6) = 1/6 + 1/6 + 1/6 = 3/6 = 1/2;
Вероятность одновременного появления двух или более независимых событий равна произведению вероятностей каждого из них.
Р (А и В и С)= Р (А) * Р (В) * Р (С)
Это теорема произведения вероятностей.
Пример. Найдите вероятность того, что в семье из трех детей родятся два сына и одна дочь.
Вероятность рождения мальчика Р(А) = 0,515, вероятность рождения девочки Р(В) = 0,485.
Р (А и В и С) = Р (А) * Р (В) * Р (С) = 0,515 * 0,515 * 0,485 = 0,129
Рассмотрим простую задачу из теории игр. Из урны ,в которой среди 10 шаров, имеется 6 белых, извлекают последовательно шары, не возвращая их обратно. Определить вероятность того, что второй извлеченный шар окажется белым .Вероятность извлечения первого белого шара Р(А)= 6/10. А вероятность извлечения второго белого шара зависит от того, имело ли первое событие место. Если первым был белый шар, то вероятность извлечения второго белого шара равна Р(В)=5/9. Если первый шар не белый, то Р(В)=6/9. Таким образом, вероятность наступления второго события зависит от первого события. Такая вероятность наступления события называется условной вероятностью и обозначается РА(В) - если первое событие имело место, Р-A(В) - если первое событие не имело место. А - событие противоположное событию А.
Сумма вероятностей всех возможных событий при данном испытании равна 1:
Р(А)+Р(В)+Р(С) +... = 1
Изучая какое-либо явление, мы всегда имеем дело с совокупностью величин, описывающих его. Эти величины даже для одного и того же явления несколько изменяются, варьируют в различных измерениях. Особенно это положение относится к области биологии и медицины, где эти изменения могут быть весьма существенными, т.к. развитие живого организма определяется очень многими и разнообразными условиями внутреннего и внешнего порядка. Поэтому, в результате изучения у ряда особей какого-либо качественного или количественного признака будет получаться не одно, а целый ряд значений, обычно не совпадающих между собой.
Такие величины, которые в зависимости от обстоятельств могут принимать те или иные значения, называются случайными величинами. Случайная величина, принимающая только определённые числовые значения, называется дискретной.
Например: оценка, полученная на экзамене - 2, 3, 4, 5, номера выигрышных билетов в лотерее, число форменных элементов в крови, количество заболеваний и др.
Случайные величины обозначаются X, Y, Z, ..., а их возможные значения – х1, х2, х3,..., хi,... хn; у1, у2, у3,... ,yi;... уn.
Представление возможных значений дискретной случайной величины и соответствующих им вероятностей называют законом или функцией распределения случайной величины.
Закон или функция распределения могут быть заданы графически, аналитически, в виде таблицы. На практике дискретные случайные величины характеризуются числовыми параметрами, связанными с законом распределения. Это математическое ожидание, дисперсия, среднее квадратичное отклонение.
Математическим ожиданием случайной величины называется сумма произведений всех её возможных значений на их вероятности.
М(Х) = ∑ xiPi
Отдельные значения случайной величины группируются около математического ожидания. Степень рассеивания характеризуется дисперсией.
Дисперсией называется математическое ожидание квадрата отклонения случайной величины от её математического ожидания.
Можно доказать, что D(X) = ∑ Рi [хi - М (X)]2 Средним квадратичным отклонением случайной величины называется корень… σ(X) = (D(X))1/2Величина, принимающая любые значения в определенном интервале, называется непрерывной.
Такую функцию распределения непрерывной случайной величины называют плотностью вероятности.
В качестве примера рассмотрим экспериментальное распределение биопотенциалов, измеренных у 100 электрических скатов в момент возбуждения. В этой… - весь диапазон измеренных напряжений разбивают на несколько интервалов (в… - определяют средину каждого интервала - < xi >,Распределение Максвелла
Φ(υ) = (m0/2 πkT)1/2 * e-m0 υ2/2kT здесь, m0 - масса молекулы, k - постоянная Больцмана, Т - абсолютная…Распределение Больцмана
N = n0-mqh/kT здесь n - концентрация на высоте h, n0 - у поверхности земли. Поделив обе… n/no = e-mqh/kT; φ(h)e-mqh/kTНормальный закон распределения
φ(X) = 1/((2π)1/2σ) * e((x – a)2/2σ2)1/2 Это распределение называется - нормальный закон распределения. Здесь а -… φ(X) = 1/((2π)1/2σ)Медиана (Me) - средняя, относительно которой ряд распределения делится на две части; в обе стороны от медианы располагается одинаковое число ранжированных значений измеренной величины.
Например, для ряда 12, 14, 16, 18, 20, 22, 24, 26, 28 медианой будет число 20: по обе стороны располагаются по 4 значения.vДля ряда с четным числом значений (6, 8, 10, 12, 14, 16, 18, 20, 22, 24) медиана определяется как полусумма центральных членов Ме = (14+16)/2= 15
Мода (Мо) - это величина или качественный признак, который включает наибольшее число вариант.
Интервал (класс), в котором наибольшее число вариант, называется модальным классом.
Медиана определяется по формуле: Me = xn + λ((m2 – m1)/(2m2 – m1 – m3))
где хn - нижняя граница модального класса, λ - ширина модального класса, m1, m2, m3 - соответственно: частота класса, предшествующего модальному; частота самого модального класса; частота последующего за модальным классом. В приведенном примере
Me = 11.8 + 0.7((25-23)/(2*25 – 23 -17)) =12.9
На представленном графике дано распределение по возрасту заболевших дифтерией (по вертикальной оси - количество заболевших на 10 тыс. человек, по горизонтальной - возраст). Величина математического ожидания М(Х)=7,75 практически не несет информацию о данном заболевании, а величина моды Мо = 3 определяет в каком возрасте наиболее часто происходят заболевания и необходимо осуществлять профилактические мероприятия. Кроме медианы и моды для характеристики выборочных распределений используются также рассмотренные выше параметры: математическое ожидание, дисперсия и среднее квадратичное отклонение.
Нормальное теоретическое распределение графически представлено четко выраженной симметричной линией (1) на рис.

Однако выборочные распределения могут отличаться от нормального высотой максимального значения распределения - кривая (2). Это отличие характеризуется специальным параметром - эксцессом распределения. Экспериментальное распределение может быть несимметричной кривой (3). Такие отклонения также характеризуются специальным параметром - асимметрией распределения. Для биологических объектов характерно то, что они в большинстве представляют однородные популяции (виды, породы, сорта и др.). Изучение какого-либо признака у всех особей популяций дало бы множество несколько отличающихся друг от друга значений случайной величины, характеризующей данный признак.
Все множество возможных значений случайной величины у всех особей данной популяции называется генеральной совокупностью.
Однако в эксперименте, в связи с чрезвычайной многочисленностью популяций, изучается часть особей.
Множество значений случайной величины, измеренных у отдельных особей, называется выборкой из генеральной совокупности.
Надежностью результата серии измерений называется вероятность того, что истинное значение измеряемой величины (а) попадает в выбранный… Чем больше величина доверительного интервала, т.е. чем больше (∆ά),… Теория показывает, если n >, 30, то доверительный интервал определяется следующими правилами:Предположение, что различия между объектами нет, называют нулевой гипотезой. Существование различия между объектами называют альтернативной гипотезой.
Признание одной из гипотез осуществляется с помощью так называемых критериев различия. Различают два вида критериев различия: параметрические и непараметрические. Параметрические критерии определяются через параметры распределения: математическое ожидание, дисперсию, среднее квадратичное отклонение и др. Наиболее часто употребляемые в статистике параметрические критерии: критерий Пирсона, критерий Стьюдента, F-критерий Фишера, критерий χ2 (хи-квадрат). Однако параметрические критерии имеют определенные условия, которые ограничивают их применимость для решения указанных задач. К непараметрическим критериям относятся: критерий Вилкоксона, критерий ван-дер-Вандера, серийный критерий, критерий знаков и др. Сущность и использование всех перечисленных критериев можно найти в любом учебнике по статистике. В качестве примера рассмотрим задачу определения различия между двумя выборками по критерию Стьюдента. Необходимо выяснить эффективность применения некоторого препарата, имеющего целью повысить сопротивляемость организма по отношению к определенной инфекции. Для этого берут две группы животных. В одной из них (контрольной) не вводят препарат, другой (опытной) вводят. Затем обе группы заражают и наблюдают сколько дней переживают животные опытной и контрольной группы. В одной из серий были получены следующие результаты:

Как видно, среднее значение опытной и контрольной группы различаются. Но эти различия могут быть обусловлены случайностью выборки. Для определения достоверности различия пользуются критерием Стьюдента:
1) t =│ά1 - ά2│/(σ`12 + σ`22)1/2, t = │6.25 – 5.22│/(.222 + 0.22)1/2 = 3.4,
2) n = nl+ n2 - 2 = 32 + 23 - 2 = 53,
3) определяют по п и выбранной надежности по таблице t 0,95 = 2,01,10,99 = 2,68,
4) если t > t0,99, то различие считается достоверным,
если t0,95< t <t0,99 - то различие сомнительно,
если t < t 0,95 - различия нет.
В нашем примере 3,4 > 2,68. Следовательно, данный препарат обладает защитными свойствами. Переменные величины Y и X находятся в функциональной зависимости одна от другой, если всякому определенному значению одной из них соответствует одно или несколько вполне определенных значений другой. Такие связи представляют все точные законы астрономии, физики, химии.
Например: в законе Бойля - Мариотта давление и объем связаны функциональной зависимостью. Р= C/V, где С= const. Такие зависимости легко можно выразить графически. На практике, особенно в биологии и медицине, изучаются такие зависимости, в которых каждому значению одной величины, хотя и соответствуют несколько значений другой, но число этих значений и сами значения остаются не вполне определенными. Т.е. каждому значению X соответствует не определенное значение, а распределение случайной величины Y и наоборот.
Зависимость между X и Y, если она существует, называют корреляционной или просто корреляцией.
Корреляционная зависимость между ростом и весом в данном примере, если она существует, может быть выражена графически. Для этого определяют… X = ∑xi ni/n` , Y = ∑yini/n``Сумма квадратов отклонений функции от ординаты экспериментальной линии должна быть наименьшей.
Y I → min
Пользуясь правилом наименьших квадратов, можно определить уравнение,… 1)у = ах + b: определяют а и bЭЛЕМЕНТЫ ВЫСШЕЙ МАТЕМАТИКИ
Наш курс высшей математики для студентов всех факультетов ОГМА ставит целью - изложение основных понятий высшей математики и их приложений в различных областях. Овладение ее методами и умение применять их на практике насущно необходимы для каждого естествоиспытателя - биолога, врача.
Производная от функции в данной точке
1. Задача о нахождении скорости движения материальной точки. Пусть материальная точка при переменном движении в момент времени t1,…Tgα2 = ∆y/∆x
Если точка М2 → М1, то ∆х → 0, a tgα2 → tgα1, тогда:
Tgα1 =lim∆x→0∆y/∆x
Таким образом, физическая и геометрическая задача приводят к нахождению предела отношения приращения функции к приращению аргумента, когда последний стремится к нулю - это и есть производная.
Производной от функции в некоторой точке называется предел отношения приращения функции к приращению аргумента, если приращение аргумента стремится к нулю.
Обозначается производная: f1х (х) = у1х = lim∆x→0 ∆y/∆x
Процесс нахождения производной функции, называется дифференцированием. Общий метод нахождения производной согласно определения.
Пример :у = х2-1
1. Если аргумент получил приращение ∆х, то функция получит приращение ∆у:
У + ∆у = (х + ∆х)2-1
2. Находим приращение ∆у:
У + ∆у = х2+2х∆х +∆х2-1
-
У = x2 – 1
------------------------------
У = 0 + 2х∆х + ∆х2-0
∆у = 2х∆х + ∆х2
3. Находим по определению производную функции.
Y1x = lim∆x→0 ∆y/∆x = lim∆x→0 (2x∆x + ∆x2)/∆x = lim∆x→0 (2x + ∆x) = 2x
На практике такой метод не применяется, т.к. требует громоздких вычислений. По общему правилу нахождения производных были найдены производные простейших функций, табличные значения которых приведены ниже:
1. Производная постоянного числа равна нулю.
У = const. ух' = 0. Пример: у = 2, ух' = 0.
2. Производная степенной функции.
У = хn, ух' = nхn-1. Пример: у = х3, ух' = Зх3-1 = Зх2.
3. Производная от аргумента равна единице.
У = х, у = х1, ух'=1х1-1; ух'=1х°=1.
4. Производная показательной функции,
У = аx; ух' = ах In a.
5. Производная экспоненциальной функции.
у = еx; ух' = еx
6. Производная логарифмической функции.
У = logax; у`х = 1/(x ina), 2) у = In х; у`х = 1/x
7. Производные тригонометрических функций.
У = sinx, у`х = cosxy = cosx, у`х = -sinх
Y = tgx, y`x = 1/(cos2x)y = ctgx, у`х = -1/sin2x
Некоторые правила нахождения производных
1. Постоянная величина выносится за знак производной.
y = Cf(x), y'x= C[f(x)]' y = 2/5x5, y'x=2/5[x5] = 2/55x4 =2 x4
2. Производная суммы или разности функций равна сумме или разности производных.
Y = u ± v, y'x =u`х ± v'x , y = 3x2 + lnx, y'x = 3 * 2x + 1/x = 6x + 1/x
3. Производная произведения двух функций равна произведению производной первой функции на вторую функцию плюс произведение первой функции на производную второй.
y = uv, yx =u'xv + v'xu , y = xsinx,
У`х =l sinx + x cosx = sin x+x cosx
4. Производная дроби равна также дроби, числитель которой есть разность произведения знаменателя на производную числителя и числителя дроби на производную знаменателя, а знаменатель есть квадрат прежнего знаменателя.
y = u/v, y`x = (vu`x – uv`x)/v2
y = (3x-1)/x, y`x = (x(3x – 1) - (3x – 1)x`)/x2 = (3x – 3x + 1)/x2 = 1/x2
5. Производная сложной функции.
Пусть у есть функция от аргумента Z, у = f(Z), а аргумент Z есть функция от аргумента X, Z = f(X). Тогда функция у = f[f(x)] называется сложной функцией.
Производная cложной функции по независимому переменному X равна произведению производной этой функции по промежуточному аргументу Z на производную промежуточного аргумента по независимой переменной X.
у'х =y'z * Z`x
Y=sinx2, z = x2, y = sinz, y`z =cosz, z`x =2x
Yx =y`z * z`x = 2x cosz = 2x cosx2 .
Производные второго и высших порядков
Обозначение: y``x = d2y/dx2 (де два игрек по де икс дважды). Пример: у = Зх2+2х-1 Производная I порядка: ух' = 3 * 2х + 2 * 1- 0 = 6х + 2Возрастание и убывание функции
Если первая производная функции в данном промежутке значений положительна, то функция возрастает, а если первая производная отрицательна, то функция убывает.
П р и м е р: у = 2х2 + 4х + 5, ух' = 4х + 4
При 4х + 4 > 0 т.е. х > -1 функция возрастает,
Х + 4< 0 т.е. х < -1 функция убывает.
При х = -1, у = 2(-1)2 + 4(-1) + 5 = 3. В точке х = -1 функция имеет минимальное значение (min).
Точки минимальных и максимальных значений функции называются точками экстремума.
Исследование функций на экстремум.

У одной функции может быть несколько экстремальных точек (т.е. точек max и min).
Функция имеет максимум при х = а, если первая производная в точке равна 0 и при всех х, достаточно близких к а, выполняется неравенство f(a) > f(x).
Функция имеет минимум при х = а, если первая производная в точке равна 0 и при всех х, достаточно близких к а, выполняется неравенство f(a) < f(x).
Пример: у = х2+1
У'х = 2х
Y`x = 2х = 0
Х = 0 - точка экстремума.
А) у(0) = 02 + 1 = 1
Б)у(-1) = (-1)2+1 = 2
В)у(1)= 12+ 1 =2
y(0) < y (±1), следовательно в точке х = 0, функция имеет min.

Второе правило нахождения максимумов и минимумов
Если первая производная равна 0 в точке х = а, а вторая производная f'(а) < 0, то в этой точке максимум, а если f'(a)> О, то в этой точке минимум.
Это правило используется тогда, когда вторая производная f'(x) не равна нулю.
Дифференциал функции
Пусть дана функция у = f(x). По определению ее производная
Y`х = lim∆x→0∆y/∆x
Естественно, сама производная у`х всегда отличается от отношения ∆y/∆x на какую - то малую величину α.
Y/∆x = y`x + α. Найдем отсюда ∆у: ∆у = у'х ∆х + α∆х
Так как величина α∆х ввиду малости α и очень мала, то ею можно пренебречь, поэтому называют главным приращением функции или дифференциалом функции и обозначается dy; т.е. dy = yx'∆x. Дифференциал аргумента равен его приращению: dx = ∆х, тогда
Dy = y`xdx, а y`x = dy/dx
Первая производная равна отношению дифференциала функции к дифференциалу аргумента.
Из чертежа CD = AC tg α1, AC = ∆x, a tgα = y`x (геометрический смысл производной), тогда CD = у'x dx, но yx'dx = dy;
CD = dy
Таким образом, дифференциал есть приращение ординаты касательной, соответствующей приращению аргумента ∆х.
Некоторые свойства дифференциала
1. Дифференциал суммы (разности) функций равен сумме (разности) дифференциалов функций.
У = u ± v, dy = du ± dv.
2. Дифференциал произведения двух функций:
У = u * v, dy = vdu + udv.
3. Дифференциал частного двух функций:
y =u/v, dy =( vdu – udv)/v2
4. Дифференциал произведения постоянной величины на функцию.
D(Cy) = Cdy
Неопределенный интеграл
Например: Дана производная функции у1x=5х4 или ее дифференциал dy = 5x4dx. Определить саму функцию у = F(x). Такую функцию называют первообразной.Первообразная функция - это функция, которая имеет производную, равную заданной.
Однако для любой функции первообразных бесконечное множество, отличающихся постоянной величиной.
Совокупность первообразных F(x) + с, производная которых равна f(x), называется неопределенным интегралом и обозначается:
F(x)dx
∫f(x)dx = F(x) + C, если F'x = f(x)
f(x) - подынтегральная функция
f(x) dx - подынтегральное выражение.
Действия, состоящие в разыскивании неопределенного интеграла данной функции, называется неопределенным интегрированием.
Основные свойства неопределенного интеграла
1. Дифференциал неопределенного интеграла равен подынтегральному выражению.
D∫f (x)dx = f (x)dx.
Это свойство следует из определения неопределенного интеграла.
2. Неопределенный интеграл от дифференциала функции равен этой функции, сложенной с произвольной постоянной.
DF(x) = F(x) + C
3. Постоянный множитель выносится за знак интеграла.
F (x)dx = α∫f(x)dx ,α = const
4. Интеграл алгебраической суммы равен алгебраической сумме интегралов каждой функции.
F1(x)±f2(x)+..]dx = ∫f1(x)dx ± ∫f2(x)dx ±..
Так же как и для определения производной, наиболее часто встречающиеся интегралы, записываются в виде таблиц.
Таблица неопределенных интегралов
Xn dx = xn+1/n+1+C, n ≠ -1
Dx/x = lnx + C
Ex dx = ex+C
Sinxdx = - cosx + C
Cosxdx = sinx + C
Dx/cos2x = tgx +C
Dx/sin2x = -ctgx + C
Основные методы интегрирования
Пример: ∫ (x + l)(x - 2)dx = ∫ (x2-x-2)dx = ∫x2dx - ∫xdx - ∫2xdx = ∫(x3/3 +C1) – (x2/2 + C2) - (2x + C3) = x3/3… 2. Метод подстановки (замены переменной). Пример: ∫e3xdx = 1/3∫ezdz = 1/3ez + C = 1/3e3x + C.Du = dx/x и v =x
Подставляя в формулу (1), находим решение:
Lnxdx = xlnx - ∫x(dx/x) = xlnx - ∫dx = xlnx - x + C = x(lnx-l) + C.
Пример: Найти уравнение пути равноускоренного движения.
А = (υt – υ0)/ t, υt = υ0 + at, υt = dS/dt, dS = υtdt, dS = (υ0 =at)dt.
Интегрируем обе части равенства.
DS = ∫ (υ0 +at)dt = ∫dS = υ0 ∫dt + a∫tdt, S = υ0t + at2/2 + C.
В момент t = 0, S = 0 и С=0, тогда S = υ0t + at2/2
Определенный интеграл
S = f(x1)∆x1 +f(x2)∆x2+...+ f(xn)∆xn = ∑f(xi)∆xi Более точно мы определим площадь, если будем разбивать интервал [ab] на… Sжт.Тт = lim∆x→0∑f(xi)∆xi,Определенный интеграл от функции равен разности первообразной этой функции в подстановке верхнего и нижнего пределов.
F(x)dx=F(x)|ba = F(b) - F(a).
Некоторые свойства определенного интеграла
1. При перестановке местами пределов интегрирования знак интеграла меняется на противоположный.
Ba f(x)dx = -∫ba (x)dx.p
2. Постоянный множитель выносится за знак определенного интеграла.
Ba Cf(x)dx = C∫ba f(x)dx.
3. Определенный интеграл от алгебраической суммы функций равен алгебраической сумме определенных интегралов от каждой функции в отдельности.
Ba [f1 (x) ± f2(x) ±...± fn(x)]dx = ∫ba fl(x)dx ± ∫ba f2(x)dx ±...± ∫ba fn(x)dx.
4. Если функция f(x) на отрезке [ab] отрицательна, то для вычисления площади интеграл нужно брать с отрицательным знаком.
Ba f(x)dx
5. Если функция f(x) пересекает ось ОХ, то для вычисления площади необходимо разбивать определенный интеграл на два: один для положительных значений f(x), второй для отрицательных.
∫ba f (x)dx = ∫ca f (x)dx – ∫bc f (x)dx.
Техника вычисления определенного интеграла
Общее правило:
1. Найти неопределенный интеграл, т. е. первообразную функцию.
2. Найти разность первообразных функций при подстановке верхнего и нижнего пределов.
Пример: ∫10 (l – x)1/2dx = -∫01 z1/2dz = -2/3z3/2|01 = 2/3
Z = 1 - х, dx = -dz
Пример: Вычислить площадь фигуры, заключенную между функцией у = х2 в интервале от 1 до 2.
S= ∫21 x2dx = x3/3│21 = 23/3 – 13/3 =8/3 – 1/3 = 7/3 кв.ед.
Дифференциальные уравнения
Дифференциальными уравнениями описываются различные процессы и явления в физике, химии, биологии и медицине. Они позволяют, в частности, определять изменение состояния различных биологических систем со временем, создавать и анализировать математические модели многих функциональных систем человека.
Дифференциальным уравнением называется уравнение, связывающее независимую переменную х, искомую функцию и ее производные.
F(x, y, y`x, y``x, ...) = 0.
Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение.
Решением или интегралом дифференциального уравнения называется всякая функция f(x), которая будучи подставлена в уравнение, превращает его в тождество.
Дифференциальное уравнение имеет бесчисленное множество решений. Чтобы получить единичное решение, необходимо задать начальные условия (х = х0), у(х0) = у0.
Общим решением дифференциального уравнения называется функция у = f(x,C), которая зависит от произвольной постоянной С. Частным решением дифференциального уравнения называется любая функция у = f(x), которая получается из общего решения, если в последнем произвольному постоянному С придать определенное значение Со, которое определяется начальными условиями.
Пример: дано равенство y`х = 2х, dy/dx = 2х или dy = 2xdx .
Можно найти уравнение кривой, т.е. выразить переменную у как функцию от х. Для этого интегрируем левую и правую части: ∫dy = 2∫xdx, получаем у = х2 + С, где С произвольная постоянная. При любом значении постоянной С дифференциал выражения dy = 2x dx, при замене у выражением х2 + С, приводит к тождеству d(x2 + С) = 2х dx. Таким образом, решением уравнения служит не одна, а бесчисленное множество функций, определяемых выражением х2 + С и отличающихся только значением постоянной С.
Дифференциальные уравнения с разделенными и разделяющимися переменными
Дифференциальное уравнение типа f(x)dx + f(y)dy=0 называется уравнением с разделенными переменными. Решение определяется интегрированием: ∫f(x)dx + ∫f(y)dy = 0
Пример: xdx + ydy = 0, ydy = -xdx, ∫ydy = - xdx, y2/ = x2/2 + C или y2/2 + x2/2 = C2/2
Дифференциальные уравнения типа f(x)f(y)dx + φ(x)φ(y)dy = 0 называются дифференциальными уравнениями с разделяющимися переменными.
Их можно привести к уравнениям с разделенными переменными, разделив на f (у)φ(х).
тогда (f(x)f(y)dx)/(f(y)φ(x) + φ(x)φ(y)dy)/f(y)φ(x), получим
F(x)/φ + φ(y)f(y)dy
F(x)/φ(x)dx + ∫φ(y)/f(y)dy + 0
Пример: ydx - xdy = 0 , разделим на
ydx/xy - xdy/xy = 0, dx/x – dy/y = 0, ∫dy/y = ∫dx/x,
Ln у = ln x + lnС, ln у - In С = ln x, lny/C = In x, x/C = x, y = Cx
Задачи на составление дифференциального уравнения
где L - концентрация препарата в органе (условные единицы), В - коэффициент, характеризующий скорость переноса…DL/dt = - BL, dL = - BLdt, dL/L = - Bdt, ∫dL/L = - B∫dt
LnL = - Bt + lnC, lnL - lnC = -Bt, lnL/C = - Bt, L = Ce-Bt.
При t = 0, С = L0, тогда L = L0 • e-Bt.
2. Модель непрерывного введения препарата в орган.

L - условная концентрация препарата в органе. В - коэффициент, характеризующий скорость переноса препарата из органа в кровь. Q - скорость введения препарата в орган. Составим дифференциальное уравнение:
DL/dt = Q -BL, dL (Q – BL) = dt, ∫dL/(Q – BL) = ∫ dt. Обозначим Q - BL = у, dy = -BdL, dL = - dy/B, тогда – 1/B∫dy/y =∫dt, ∫dy/y = - B∫dt
Ln y = -Bt + lnC, ln y – ln C = -Bt, ln y/C = -Bt, y = C * e-Bt.
Подставим вместо у его значение Q - BL: Q - BL = С * e-Bt.
При t = 0, L = 0, С = Q, тогда Q - BL = Q * e-Bt, BL = Q - Q * e-Bt, BL = Q(l - e)-Bt,
L = Q/B(l - e-Bt).
3. Терапевтический эффект некоторого лекарственного препарата сохраняется до его концентрации, составляющей 10% начальной концентрации в момент приема препарата. Определить сколько раз в сутки следует принимать препарат, чтобы его эффект сохранялся непрерывно. Известно, что через 1 час 12 минут концентрация препарата уменьшается в два раза. Скорость усвоения препарата пропорциональна его концентрации.
С - концентрация вещества в любой момент времени.
Со - концентрация в момент времени t = 0.
К - коэффициент пропорциональности,
при t = 72 мин.; C = С0/2
C1 = 0,1С
N - ?
1. Определим закон (формулу) по которой происходит разложение лекарственного препарата:
dC/dt = -KC, dC/C = -Kdt, ∫ dC/C = -K∫dt,
In С = -Kt + In А, где А - произвольная постоянная интегрирования,
lnC - lnA = -Kt, InC/A = -Kt, C=A * e-Kt
При t = 0, С = С0, тогда C0 = A * e-K0, A = C0, C = C0 * e-Kt.
2. Чтобы найти К, воспользуемся условием С = C0/2 при t =72
C0/2 = C0 * e-72K, 1/2 = e-72K, 2 = e72K, ln2 = 72K, K = 0.693/72, K =0.00962.
3. Находим время, через которое концентрация препарата станет равной: С1 =0,1 С0.
С0 = Со * e-0.09625t, 0,1 = е-0.0096251, ln10 = e-0.009625', ln 10 = 0,009625t
Ln 10 = 2,32, 3 = 0,009625t, t = 2.3/0.009625 = 240 (мин) = 4 часа, тогда n = 24/4 = 6 (раз в сутки).
4. При расследовании убийства температура тела убитого оказалась равной 20f С, а температура воздуха 150 С. Скорость охлаждения пропорциональна разности температур тела и воздуха. Определить время, прошедшее с момента убийства.
ТО = 36,6°С
Тт = 20 °С - температура тела убитого
Тв = 15 °С
Т - температура тела в любой момент времени
К = 0,0069 мин-1 - определяется опытным путем
T - ?
dT/dt = -K(T – TB), ∫dT/(T – TB) = -K∫dT, ln(T – TB) = -kT + lnC,
Ln((T – TB)/C) = -Kt, T – TB = C * e-Kt, T = TB + C * e-Kt.
При t = 0, T = T0, C = T0 – TB.
В момент обнаружения тела убитого Т = Тт, тогда Тт = ТB + (То - ТB) * e-Kt, подставляем значения температур: 20 = 15 + 21,6 * e-Kt,
eKt = 21.6/5, Kt = ln21.6/5, t = ln4.3/.0069 =210 (мин)
Убийство произошло за 3,5 часа до момента расследования.
КИБЕРНЕТИКА И ИНФОРМАТИКА
Кибернетика - наука о законах управления и оптимальном использовании информации в сложных динамических системах управления.
Предметом исследования кибернетики является обмен информацией, оценка функционирования систем управления и их взаимосвязь. Основным методом кибернетики является метод математического моделирования… Основным принципом кибернетики является применение системного подхода при описании и исследовании сложных систем.Информатика - научная дисциплина, изучающая структуру и общие свойства научной информации, а также закономерности всех процессов научной коммуникации.
Значительную часть этих процессов составляет научно-информационная деятельность по сбору, переработке, хранению, поиску и распространению научной информации. Основная теоретическая задача информатики заключается в определении общих закономерностей, в соответствии с которыми происходит создание научной информации, ее преобразование, передача и использование в различных сферах деятельности человека. Математическая теория информации используется в информатике для обеспечения оптимального кодирования информации, ее долговременного хранения, поиска и передачи на расстояние.
Математическая теория информации - раздел кибернетики, занимающийся математическим описанием и оценкой методов передачи, хранения, извлечения и классификации информации.
Она в основном математическая дисциплина, использующая методы теории вероятности, математической статистики, линейной алгебры и др. Первоначально теория информации возникла как теория связи, обеспечивающая надежность и экономичность передачи сообщений по техническим каналам связи. Сейчас она является универсальной теорией связи для систем любого происхождения, в том числе и биологических. Недостаточное к ней внимание биологов и медиков обусловлено, вероятно, их слабой осведомленностью в этой области. Хотя, даже на первый взгляд ясно, что теория располагает неограниченными возможностями описать, дать количественную характеристику сложных биологических объектов. И не случайно поэтому, в начале медицинская кибернетика (1975 г.), а затем информатика введена в программу медицинских вузов.
Информация так же как масса и энергия является характеристикой окружающего нас мира, это философская категория, материальная субстанция, характеризующая пространственную ориентацию материи.
Информация - это совокупность каких-либо сведений, данных, знаний об изучаемом объекте, явлении, процессе.
Количество информации зависит от числа сообщений (N), точнее прямо пропорционально логарифму от N:J = logaN
Основанием логарифма берется, как правило, число 2, т.к. в принципе, любую информацию можно представить в виде совокупности двух цифр - «0» и «1» («0» - нет, «1» - да), тогда
J = log2N.
Если в этом определении N = 2, то J = log22 = 1. '
Количество информации равно единице, когда число сообщений равно двум. Такая единица измерения количества информации получила название БИТ.
Пример: Подсчитать количество информации, которую несет одна буква русского алфавита. Приближенно будем считать N = 32 и использование каждой… Следовательно, каждая буква русского алфавита несет информацию в 5 бит, если… Преобразуем: J = logN = -log1/NЦенность информации - это изменение вероятности достижения цели, в результате получения информации.
где Р1 - вероятность достижения цели до получения информации, Р2 - после. Ценность информации бывает как положительной, так и отрицательной.… Как видно из данной схемы, передача информации предполагает наличие…ОСНОВЫ ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
Вычислительная техника - это совокупность механических и электронных средств автоматизации вычислений и обработки информации.
К центральным устройствам относятся: 1. Арифметическое устройство (АУ). 2. Устройство управления (УУ).ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ ЭВМ
Чтобы войти в какой-либо файл, содержащийся в каталоге, нужно войти сначала в каталог, а затем в нужный файл, для его…Краткий формат
Полный формат
Состояние
Дерево каталогов
Просмотр
Архив
Панель поиска
Alt-F1 - выбор диска, изображаемого на левой панели; Alt-F2 - выбор диска, изображаемого на правой панели; Alt-F3 - просмотр текстового файла. Этот режим вызывается быстрее, но позволяет просматривать только текстовые файлы и…Для входа в меню нажмите Fl0 0 1 2 3 4 5 6 7 8 9 0
Текст Лексика Абзац Фрагмент Страницы Найти
Заменить Метка Прыг Шрифт ДОС Выхрд
ДОК РАВ ПЕР ШРО D:lexl.txt (472 198.44) РУС 25 мар 12:28
Третья строка информационная, в ней имеется четыре поля. В первом поле высвечиваются режимы работы редактора. Во втором - имя файла и координаты… В информатике, программировании существует такое понятие - базы данных. Под… СУБД позволяет активно работать с этой информацией:Рассмотрим наиболее часто употребляемые в Бейсике операторы.
10. LET A=5 (пусть А равно 5) 10. LETA=B*10 10. LET А=В^3ТЕХНИКА ЭЛЕКТРОБЕЗОПАСНОСТИ ПРИ РАБОТЕ С ЭЛЕКТРОННЫМИ МЕДИЦИНСКИМИ СИСТЕМАМИ
К потребителю подводится 4 провода - три фазных и один нулевой. Напряжение между нулевым проводом и любой фазой составляет 220 В и называется… Таким образом требования электробезопасности при контакте "человек -… Любой медицинский прибор, питающийся от сети переменного тока, с точки зрения электробезопасности можно представить…J = 220B/1000OM = 0.22A (в два раза больше "летального").
На практике на металлическом корпусе прибора, за счет плохой изоляции проводов, за счет индуктивной и емкостной связи, возникают потенциалы от нескольких вольт до десятков вольт относительно земли. Электробезопасность такого прибора определяется ?током утечки?. Величина тока утечки равна отношению наведенного потенциала на корпусе к сопротивлению 1 КОм. Такой ток протекал бы через человека при одновременном касании корпуса прибора и земли. При заземлении корпуса поражающего действия не оказывается. Уменьшить величину тока через организм при случайном касании корпуса прибора или фазных проводов можно, изолировав человека от земли, например, резиновым ковриком. В этом случае ток через организм человека будет определятся по формуле:
J = U/Rч + Rиз
Rиз равна несколько МОм, а ток практически равен 0.
Аналогичное же действие оказывает и постоянный ток, но его величина должна быть приблизительно в 3 раза больше. Несоблюдение правил техники безопасности при работе с электронными медицинскими приборами, является недопустимым грубейшим нарушением, которое при определенных ситуациях может повлечь за собой человеческие жертвы.
Электробезопасность достигается соблюдением трех основных видов защиты:
1.Правильной конструкцией аппаратуры, дающей безусловную безопасность. Безусловная электробезопасность обеспечивается выполнением основных требований к конструкции и изготовлению электронного прибора, при этом, безопасность выполняется как при нормальной эксплуатации, так и при единичных нарушениях (неисправностях). Медицинские электронные приборы рассчитаны на безусловную электробезопасность или, как говорят, рассчитаны на "дурака".
2.Указанием условий, при которых работа с оборудованием безопасна их называют относительной или описательной безопасностью (она дается в паспорте прибора). Описательная безопасность - условия, при которых работа с оборудованием безопасна. Это меры по контролю и испытанию медицинского оборудования, описательный характер штатной эксплуатации и др.
3. Применением специальных средств внешней защиты, которые дают условную безопасность. Условная безопасность обеспечивается специальными дополнительными средствами внешней защиты в зависимости от класса защиты.
Классы защиты условной безопасности
«0» - безопасность изделий обеспечивается только одной изоляцией. Примеры: бытовые приборы. Медицинская техника этого класса не изготовляется.
«1» - кроме изоляции токонесущих элементов, безопасность обеспечивается автоматическим заземлением прибора (специальная сетевая вилка с заземлением).
«01» - сетевая вилка обычная, но имеется дополнительное заземление корпуса отдельным проводом. Такой класс защиты имеет большинство медицинских приборов. Напряжение на пробой - 1500 В.
«II» - изделия с двойной усиленной изоляцией токонесущих элементов и корпуса прибора, заземление при этом отсутствует. Это электронные устройства повышенного класса безопасности. Напряжение на пробой - 4000 В. Примеры: аппарат для гальванизации, электростатдуш.
«III» - оборудование 3-го класса характеризуется низким (менее 24 В) питающим напряжением, что, наряду с основной изоляцией, является дополнительной мерой защиты от опасности электроудара, исходящей от сетевой части. Это оборудование обычно не заземляется.
Заземление электронных приборов там, где оно предусмотрено конструкцией, должно быть обязательным и надежным: постоянный и надежный контакт, низкоомная линия отведения (сопротивление от корпуса до шины заземления не более 0,4 Ома).
Заземление пациента нужно рассматривать как необходимое зло, а не как меру предосторожности и по возможности избегать его. В качестве примера, когда заземление пациента необходимо, можно привести заземление пациента при снятии ЭКГ. С точки зрения электробезопасности одновременное использование нескольких диагностических или лечебных приборов или их комбинаций на одном и том же объекте крайне нежелательно (опасно). Тем более не допустимо, подсоединение в комбинацию технических устройств других приборов, как правило, не имеющих должных устройств защиты, предъявляемых к медицинским приборам. Применение одномоментной комбинации приборов в каждом отдельном случае требует специального анализа и привлечения компетентных лиц на предмет отработки условий безопасности. При манипуляциях на СЕРДЦЕ и других жизненно важных органах требования электробезопасности еще более жесткие, так как порог фибрилляции при контактном воздействии очень низкий и составляет 10 - 100 мкА..
– Конец работы –
Используемые теги: Колебания, волны, Звук0.069
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: КОЛЕБАНИЯ, ВОЛНЫ, ЗВУК
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов