рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Энергетика
- /
- Кинетическая энергия вращающегося тела и работа вращения
Реферат Курсовая Конспект
Кинетическая энергия вращающегося тела и работа вращения
Кинетическая энергия вращающегося тела и работа вращения - раздел Энергетика, Б-1 Кинематические Уравнен...
Б-1
Кинематические уравнения движения, траектория, путь.
1. Кинетическая энергия вращающегося тела и работа вращения.
2. Термодинамические системы. Термодинамические параметры и процессы.
Равновесное состояние термодинамического процесса, Обратимые и круговые процессы
1. Кинематические уравнения движения.
При движении т.М ее координаты и 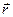 меняются со временем для задания закона движения необходимо указывать вид функциональной зависимости от времени всех трех её координат, либо
меняются со временем для задания закона движения необходимо указывать вид функциональной зависимости от времени всех трех её координат, либо 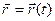 ;
; 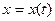 ;
; 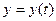 ;
; 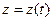 . Эти уравнения называются кинетическими уравнениями движения точки.
. Эти уравнения называются кинетическими уравнениями движения точки.
Траектория — линия описываемая точкой при ее движении относительно выбранной системы координат. Уравнение траектории можно получить из кинематических уравнений, исключив время. Различают прямолинейное и криволинейное движение плоская траектория, объемная.
Длина пути расстояние 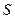 , пройденное за рассмотренный промежуток
, пройденное за рассмотренный промежуток 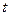 и изменяемое вдоль траектории в направлении движения; т.е.
и изменяемое вдоль траектории в направлении движения; т.е.  .
.
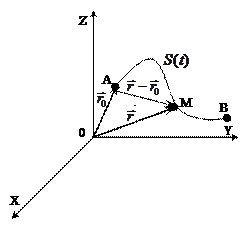
Пусть точка движется от А к В по криволинейному пути АВ в начальный момент в т.А (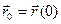 ) а в
) а в 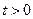 находится в т.М с
находится в т.М с 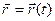 ; S=длина траектории.
; S=длина траектории.
2. Кинетическая энергия вращающегося тела.
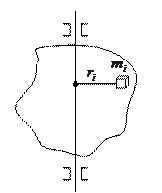 Рассмотрим абсолютно твердое тело, вращающееся вокруг неподвижной оси, проходящей через него. Разобьем его на частицы с малыми объемами и массами
Рассмотрим абсолютно твердое тело, вращающееся вокруг неподвижной оси, проходящей через него. Разобьем его на частицы с малыми объемами и массами 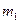 ,
,  …. находящиеся на расстояние
…. находящиеся на расстояние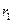 ,
, 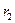 … от оси вращения. Разным
… от оси вращения. Разным  будут соответствовать, разные
будут соответствовать, разные  ,
,  … кинетическая энергия вращения всего тела сложится из энергий составляющих его частицу
… кинетическая энергия вращения всего тела сложится из энергий составляющих его частицу
 т.к.
т.к. 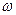 всех частиц одинакова, то
всех частиц одинакова, то 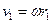 ,
,  … тогда
… тогда
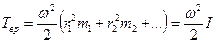 т.е.
т.е. 
Формула справедлива для тела. которое вращается вокруг неподвижной оси. Если тело катится (шар, колесо, и т.д.), то энергия движения складывается из энергии вращения и энергии поступательного движения, т.е. для тела массой 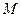 , моментом инерции
, моментом инерции 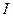 , скоростью поступательного движения
, скоростью поступательного движения 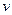 и вращения
и вращения 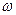
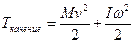 ;
;  ;
;
формула справедлива для произвольного движения, поскольку его можно разложить на совокупность вращения относительно оси инерции и поступательного движения.
Работа вращения тела.
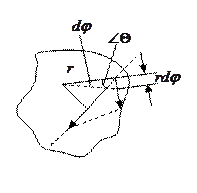 Если тело приводится во вращение силой
Если тело приводится во вращение силой 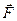 , то его вырастает на величину затраченной работой. Также как и в поступательном движении эта работа зависит от
, то его вырастает на величину затраченной работой. Также как и в поступательном движении эта работа зависит от 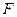 и произведено перемещение. Однако перемещение теперь угловое и выражение для работы при перемещении материальной точки неприменимо. Т.к. тело абсолютно твердое, то работа силы
и произведено перемещение. Однако перемещение теперь угловое и выражение для работы при перемещении материальной точки неприменимо. Т.к. тело абсолютно твердое, то работа силы 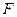 (хотя она приложена в точке) равна работе, затраченное на поворот всего тела. При повороте на угол
(хотя она приложена в точке) равна работе, затраченное на поворот всего тела. При повороте на угол 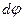 точка приложения силы проходит путь
точка приложения силы проходит путь  и работа
и работа 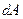 равна произведению проекции
равна произведению проекции 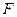 на направление смещения на величину смещения
на направление смещения на величину смещения 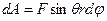 ;
; 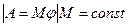 ;
;  —момент силы;
—момент силы;  —плечо силы; т.е.
—плечо силы; т.е. 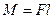
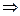
 . Работа вращение идёт на увеличение кинетической энергии
. Работа вращение идёт на увеличение кинетической энергии 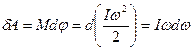 ;
; 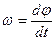 ;
; 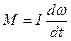 .
.
Ось, положение которой в пространстве остаётся неизменным при вращении вокруг неё тела в отсутствии внешних сил (со стороны, например, подшипников) называется свободной осью тела.
|
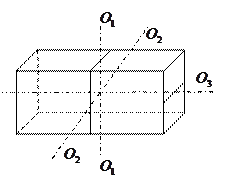 Можно доказать, что для тела любой формы с произвольным распределением массы существуют 3 взаимно
Можно доказать, что для тела любой формы с произвольным распределением массы существуют 3 взаимно 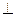 , проходящие через центр масс тела оси, которые могут служить свободными осями; они называются главными осями инерции тела.
, проходящие через центр масс тела оси, которые могут служить свободными осями; они называются главными осями инерции тела.
Моменты инерции относительно главных осей называется главным моментом инерции тела.
 Для некоторых тел с надлежащим распределением масс
Для некоторых тел с надлежащим распределением масс 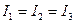 (шар куб и т.д.). Эти тела называются шаровыми волчками. Характерным для них является то, что любая ось, проходящая через С обладает свойствами свободной оси, и, следовательно, ни одна из главных осей инерции не фиксирована, как и для шара.
(шар куб и т.д.). Эти тела называются шаровыми волчками. Характерным для них является то, что любая ось, проходящая через С обладает свойствами свободной оси, и, следовательно, ни одна из главных осей инерции не фиксирована, как и для шара.
Тела с 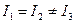 ведут себя как однородные тела вращение их называют симметричными волчками.
ведут себя как однородные тела вращение их называют симметричными волчками.
3. Термодинамические системы. Термодинамические параметры и процессы
Макросистема, рассматриваемая методами термодинамики, называется термодинамической (т.) системой. Это может быть, например, жидкость и пар, находящийся с ней в равновесии. Система может быть открытой или закрытой (в зависимости от того, обменивается ли она веществом с окружающими телами), изолированной (если нет обмена энергией с внешними телами).
Т. система может находиться в различных состояниях, отличающихся физическими величинами  , называемых т. параметрами состояния. Состоянию газа отвечают также определенная масса и химический состав вещества.
, называемых т. параметрами состояния. Состоянию газа отвечают также определенная масса и химический состав вещества.
Если параметры т. системы неизменны во времени и в системе отсутствуют потоки энергии и вещества, такое состояние т. системы называют равновесным. В такое состояние придет тело, если его изолировать от других тел и предоставить самому себе. Все его т. параметры (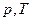 и др.) через некоторое время примут одинаковые для всех точек тела значения – тело перейдет в равновесное состояние.
и др.) через некоторое время примут одинаковые для всех точек тела значения – тело перейдет в равновесное состояние.
Процесс перехода системы из равновесного состояния в неравновесное (или наоборот) называется релаксацией. Время, в течение которого физическая величина, возвращаясь в равновесное состояние, изменяется в 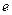 раз, называется характеристическим временем релаксации.
раз, называется характеристическим временем релаксации.
В равновесном положении система может находиться сколь угодно долго. Оно может быть изображено точкой на координатной плоскости, образованной какими-либо двумя параметрами состояния. Неравновесное состояние не может быть изображено точкой, т.к., хотя бы один параметр системы не будет иметь определенное значение для всего его объема.
При переходе из одного т. состояния системы в другое равновесие нарушается, значит, система проходит через последовательность неравновесных состояний. Нарушение равновесия тем сильней, чем быстрее проходит процесс перехода. Следовательно, при очень медленном переходе состояние системы в каждый момент является квазиравновесным. Значит, бесконечно медленный процесс перехода будет состоять из последовательности равновесных состояний. Такой процесс называется равновесным или квазистатическим.
Равновесный т. процесс может быть проведен в обратном направлении, при этом система будет проходить через те же состояния, что и при прямом переходе, но в обратной последовательности. Поэтому, равновесные процессы называют также обратимыми. Они могут быть изображены на координатной плоскости линией.
Процесс, при котором т. система после ряда изменений возвращается в исходное состояние, называется круговым процессом или циклом. Его графиком является замкнутая линия.
Все количественные выводы термодинамики применимы только к равновесным состояниям и обратимым процессам.
Б-2
1. Вектор перемещения, элементарное перемещение и путь, средняя и мгновенная скорость.
2. Уравнение динамики вращения твердого тела.
3. Температура. Шкала Цельсия, термодинамическая температурная шкала.
1. Перемещение, элементарное перемещение.
Вектором перемещения точки за промежуток от  до
до  называется приращение радиус-вектора
называется приращение радиус-вектора 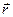 этой точки за этот промежуток
этой точки за этот промежуток  он направлен вдоль хорды стягивающий соответствующий участок траектории точки. Поэтому во всех случаях, кроме премера, модуль перемещения меньше длины пути за этот же
он направлен вдоль хорды стягивающий соответствующий участок траектории точки. Поэтому во всех случаях, кроме премера, модуль перемещения меньше длины пути за этот же 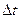 . На рисунке вектор перемещения
. На рисунке вектор перемещения 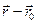 .
.
Однако, по мере уменьшения длины пути разность между хордой и перемещением уменьшается. Следовательно, рассматривая элементарное перемещение 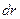 по траектории за достаточно малый промежуток вреени
по траектории за достаточно малый промежуток вреени 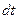 (от
(от 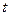 до
до 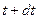 ) можно пренебречь отличием между
) можно пренебречь отличием между 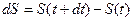 и
и 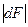 . Значит, вектор
. Значит, вектор 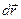 направлени по касательной к траектории в сторону движения точки. Также ка единичный вектор касат.
направлени по касательной к траектории в сторону движения точки. Также ка единичный вектор касат. 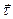 т.о.
т.о. 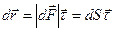 вектор перемещения материальной точки за любой конечный промежуток времени от
вектор перемещения материальной точки за любой конечный промежуток времени от 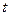 до
до 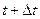 можно представить в виде:
можно представить в виде:
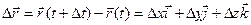
 приращение координат за
приращение координат за 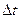 .
.
P.S.: В математике 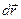 и
и 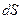 - дифференциалы соответствующих функций времени ??? т.е. линейные части приращений этих функций при произвольном изменении аргумента от
- дифференциалы соответствующих функций времени ??? т.е. линейные части приращений этих функций при произвольном изменении аргумента от 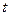 до
до 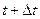 . По определению в мтематике
. По определению в мтематике 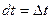
 ,
,
а 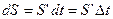 ;
;


 и
и 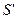 - производные т.е. приращение функций
- производные т.е. приращение функций 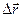 и
и 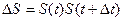 существует отличие от дифференциалов этих функций. В физике различают произвольное (конечное) приращение аргумента
существует отличие от дифференциалов этих функций. В физике различают произвольное (конечное) приращение аргумента 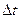 и дифференциала аргумента
и дифференциала аргумента 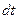 . Под дифференциалом аргумента
. Под дифференциалом аргумента 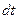 понимают столь малое его приращение (элементарное), при котором разностью между соответствующим приращением функции
понимают столь малое его приращение (элементарное), при котором разностью между соответствующим приращением функции 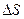 и линейной частью её приращения
и линейной частью её приращения 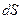 можно пренебречь т.е. ???
можно пренебречь т.е. ??? 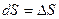 . Поэтому, в физике используют предложенные Лейбницем обозначение производной
. Поэтому, в физике используют предложенные Лейбницем обозначение производной 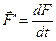
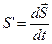 и трактуют эти выражения как отношения не математической дифференциала функции и аргумента, а малых (элеиентарных) приращений функцмм м аргумента.
и трактуют эти выражения как отношения не математической дифференциала функции и аргумента, а малых (элеиентарных) приращений функцмм м аргумента.
 Скорость.
Скорость.
Для характеристики направления и быстроты движения точки вводится векторная физическая величина-скорость.
Пусть за 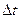 точка переместилась из т.1 в т.2. Вектор перемещения
точка переместилась из т.1 в т.2. Вектор перемещения 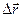 представляет собой приращение радиус-вектора
представляет собой приращение радиус-вектора 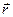 за время
за время 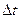
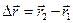 . Отношение
. Отношение  называется средней скоросью точки
называется средней скоросью точки 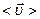 за время
за время 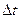 . Направление
. Направление 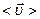 совпадает с
совпадает с 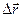 . Скорость
. Скорость  точки в заданный момент мремени определяется как предел отношения
точки в заданный момент мремени определяется как предел отношения  при
при 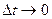 т.е.
т.е.
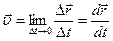
т.е. производной от радиус-вектора 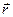 по времени и направлению по касательной к траектории в заданной точке в сторону движения. Модуль
по времени и направлению по касательной к траектории в заданной точке в сторону движения. Модуль 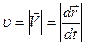 . Вектор
. Вектор  можно разложить по базису
можно разложить по базису 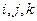 т.е. на три состояния по осям декартовой системы координат
т.е. на три состояния по осям декартовой системы координат
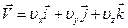 ;
;
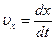 ;
;  ;
; 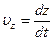 ;
;
 ;
;
2. Уравнение динамики вращения твердого тела.
Уравнение динамики твердого тела можно получить. Записав для производной момента импульса
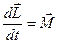 (уравнение моментов)
(уравнение моментов)
и подставив значение 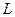 для твердого тела, вращающегося вокруг произвольной оси
для твердого тела, вращающегося вокруг произвольной оси 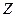 ;
;
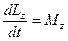 ;
; 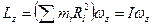

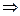
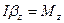 (*)
(*) 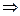
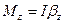 ;
;
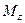 —суммарный момент всех внешних сил относительно оси вращения
—суммарный момент всех внешних сил относительно оси вращения 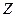 . Отсюда видно, что (сравнивая с II-ым законом Ньютона) во вращательном движении тела роль массы играет
. Отсюда видно, что (сравнивая с II-ым законом Ньютона) во вращательном движении тела роль массы играет 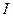 , а роль линейного ускорения
, а роль линейного ускорения 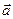 играет угловое ускорение
играет угловое ускорение 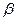 , а роль результирующей силы —суммарный момент внешних сил
, а роль результирующей силы —суммарный момент внешних сил 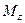 .
. 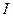 определяет инерциальные свойства. Если масса не зависит от выбора С.О. то
определяет инерциальные свойства. Если масса не зависит от выбора С.О. то 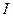 зависит от оси. Относительно которой определяется.
зависит от оси. Относительно которой определяется.
Интегрирование уравнения (*) с учетом начальных условий  и
и 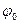 при
при 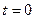 позволяет полностью решить задачу о вращении твердого тела, т.е. найти
позволяет полностью решить задачу о вращении твердого тела, т.е. найти 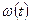 ,
, 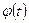 в любой момент времени в системе отсчета, жестко связанной с осью вращения.
в любой момент времени в системе отсчета, жестко связанной с осью вращения.
3. Температура
Температура системы, находящейся в равновесном состоянии, является мерой интенсивности теплового движения молекул, образующих систему. В этом состоит молекулярно-кинетическое истолкование температуры.
Если соприкасающиеся тела находятся в состоянии теплового равновесия, т.е., не обмениваются энергией путем теплопередачи, то им приписывают одинаковую температуру, а если при тепловом контакте одно из них передает энергию другому посредством теплопередачи, то первому приписывают большую температуру, второму – меньшую.
Средняя кинетическая энергия теплового движения частиц прямо- пропорциональна термодинамической температуре системы.
Для измерения температуры используется зависимость от температуры ряда физических свойств тела, называемого термометрическим, при прямом или косвенном измерении: длина, объем, сопротивление и др. Их изменение является основой для измерения температуры.
Для практического измерения температуры применяются температурные шкалы, установленные с помощью термометрических тел. В Международной стоградусной шкале в качестве термометрического тела берется вода и температура выражается в градусах Цельсия. В термодинамической температурной шкале температура выражается в К и называется термодинамической температурой. Связь между шкалами 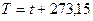 .
. 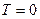 К называется абсолютный нуль температуры или нуль по термодинамической шкале.
К называется абсолютный нуль температуры или нуль по термодинамической шкале.
Б-3
1. Ускорение, тангенциальное и нормальное ускорение.
2. Принцип работы гироскопа.
3. Уравнение состояния идеального газа. Уравнение Менделеева-Клапейрона.
1. Ускорение.
Движение точки характеризуется также ускорением—быстротой изменения скорости
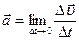 ;
; 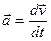
т.е. вектор 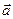 равен производной
равен производной  по времени. Направление вектора
по времени. Направление вектора 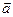 совпадает с направлением приращения скорости
совпадает с направлением приращения скорости 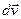 за
за 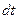 т.к.
т.к. 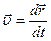 , то ускорение точки равно второй производной по времени от радиус-вектора:
, то ускорение точки равно второй производной по времени от радиус-вектора:
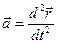 ;
; 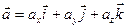 ;
; 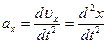 ;
;
где 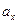 —проекция.
—проекция.
Если траектории точки плоская кривая, то можно выбрать два перпендикулярных направления: касательная к траектории (орт 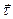 ) и нормали к ней
) и нормали к ней  . Тогда
. Тогда 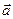 раскладывается по составляющим
раскладывается по составляющим  .
.
Т.к. вектор скорости направлен по касательной к траектории в сторону её движения, то
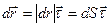 ;
;
 ;
;
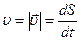 ;
; 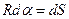
тогда 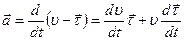 ;
; 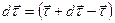 —приращение орта касательной к траектории, соответствующее элементарному пути
—приращение орта касательной к траектории, соответствующее элементарному пути  за
за 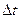 .
.
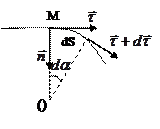 Ввиду малости
Ввиду малости 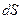 его можно считать совпадающим с дугой окружности радиуса
его можно считать совпадающим с дугой окружности радиуса  с центром в т.0 с центральным углом
с центром в т.0 с центральным углом  .
.
3. Уравнение состояния идеального газа
Состояние данной массы газа определяется значением трех параметров  , изменение одного из них приводит к изменению других. Соотношение, связывающее эти параметры, представляет собой уравнение состояния данной массы газа.
, изменение одного из них приводит к изменению других. Соотношение, связывающее эти параметры, представляет собой уравнение состояния данной массы газа.
Простейшим объектом, для которого рассмотрено уравнение состояния, является идеальный газ. Это газ, взаимодействием между молекулами которого можно пренебречь. Всякий реальный газ при достаточном разрежении близок к идеальному при комнатной температуре, особенно гелий и водород.
Экспериментально показано, что при небольших плотностях газы с хорошей точностью подчиняются уравнению:
 (1) - уравнение состояния идеального газа.
(1) - уравнение состояния идеального газа.
Согласно закону Авогадро 1 моль любого газа занимает при одинаковых условиях (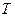 и
и 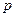 ) одинаковый объем. В частности, при нормальных :
) одинаковый объем. В частности, при нормальных : 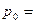 1 атм. и
1 атм. и  273К объем одного моля газа
273К объем одного моля газа 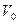 равен 22,4 л. Значит, в формуле (1) для 1 моля любого газа величина константы будет одной и той же. Она обозначается как
равен 22,4 л. Значит, в формуле (1) для 1 моля любого газа величина константы будет одной и той же. Она обозначается как  - универсальная газовая постоянная,
- универсальная газовая постоянная, 
 = 8,31Дж/моль К. Тогда уравнение состояния 1 моля газа:
= 8,31Дж/моль К. Тогда уравнение состояния 1 моля газа: 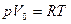 (2).
(2).
Теперь можно записать уравнение для произвольной массы газа, учитывая, что при одинаковых 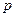 и
и 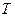 число молей
число молей  газа будет занимать объем в
газа будет занимать объем в  раз больше:
раз больше: 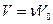 , тогда умножив (2) на
, тогда умножив (2) на  , получим:
, получим: 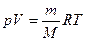 (3) – уравнение состояния для произвольной массы газа. Оно называется также уравнением Менделеева – Клапейрона.
(3) – уравнение состояния для произвольной массы газа. Оно называется также уравнением Менделеева – Клапейрона.
Если его правую часть умножить и разделить на число Авогадро, то получим:
 . Или учитывая, что
. Или учитывая, что 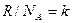 - постоянная Больцмана, а
- постоянная Больцмана, а 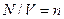 - концентрация, получим окончательно:
- концентрация, получим окончательно:
 -еще одна форма уравнения состояния идеального газа.
-еще одна форма уравнения состояния идеального газа.
| |
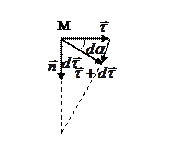 Соответственно, единичный вектор
Соответственно, единичный вектор 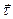 повор. на
повор. на 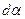 . Из равнобедренного треугольника
. Из равнобедренного треугольника 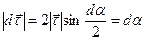 , ввиду малости
, ввиду малости 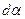 ; по направлению
; по направлению 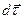 совпадает с
совпадает с  (при
(при 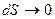
 )
)
 ;
;
и ускорение точки
 ;
;
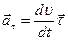 — касательное(тангенциальное) ускорение характеризует быстроту изменения модуля скорости. При ускоренном движении
— касательное(тангенциальное) ускорение характеризует быстроту изменения модуля скорости. При ускоренном движении  и
и 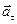 совпадает с
совпадает с  , при замедленном
, при замедленном 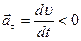 и
и 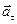 не совпадает с
не совпадает с  .
.
Нормальное ускорение 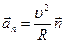 характеризует быстроту изменения направления вектора скорости. Направлено к центру кривизны траектории;
характеризует быстроту изменения направления вектора скорости. Направлено к центру кривизны траектории; 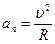 ; поэтому его называют центростремительным. При прямолинейном движении
; поэтому его называют центростремительным. При прямолинейном движении 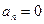 .
.
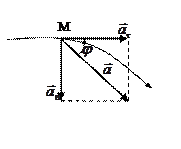 Модуль ускорения
Модуль ускорения
 ;
;
При ускоренном движении 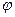 — острый, при замедленном—тупой (
— острый, при замедленном—тупой (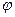 угол между
угол между 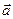 и
и 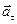 ). Если движение по окружности равномерное
). Если движение по окружности равномерное 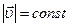 то
то 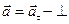 касательной.
касательной.
Б-4
1. Уравнение поступательного движения твердого тела.
2. Неинерциальные системы отсчета. Силы инерции.
3. Внутренняя энергия термодинамической системы. Внутренняя энергия идеального газа.
1. Динамика поступательного движения
2.1. Простейшим видом механического движения твердого тела является поступательное движение. при котором прямая, соединяющая любые две точки тела перемещается вместе с телом, оставаясь || своему первоначальному направлению (шарик на пружине относительно Земли, поршень в цилиндре стационарного двигателя, лифт, резец токарного станка и др.). Траектории всех точек ела известны. Радиус-вектор все точек тела за время 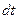 изменяется на одну и туже величину
изменяется на одну и туже величину 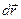 , скорости всех точек и ускорения одинаковы:
, скорости всех точек и ускорения одинаковы:
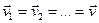 ;
; 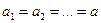
т.е. для описания можно взять одну точку, если 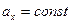 то
то

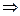
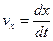

3.Внутренняя энергия системы
Полная энергия т. системы равна сумме кинетической энергии механического движения системы как целого, потенциальной энергии системы во внешнем поле ( гравитационном или электромагнитном) и внутренней энергии  , зависящей только от внутреннего состояния системы. Для неподвижных систем, не подверженных действию внешних сил, значение полной и внутренней энергий совпадают.
, зависящей только от внутреннего состояния системы. Для неподвижных систем, не подверженных действию внешних сил, значение полной и внутренней энергий совпадают.
Внутренняя энергия включает в себя энергии всевозможных видов движения и взаимодействия всех частиц (молекул, атомов, ионов и др.) системы, Например, для газа внутренняя энергия состоит из:
а) кинетической энергии теплового поступательного и вращательного движения молекул, а также колебательного движения атомов в молекулах;
б) потенциальной энергии, обусловленной силами межолекулярного взаимодействия;
в) энергии электронных оболочек атомов и ионов;
г) энергии движения и взаимодействия нуклонов в ядрах.
Внутренняя энергия является однозначной функцией состояния т.системы, Ее значение в каком –либо произвольном состоянии системы не зависит от того, каким образом пришла система в это состояние. Т.е., изменение внутренней энергии 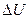 при переходе системы из состояния 1 в состояние 2 не зависит от вида процесса перехода и равно
при переходе системы из состояния 1 в состояние 2 не зависит от вида процесса перехода и равно 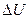
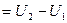 . В частности, если система возвращается в результате какого-либо перехода в исходное состояние, то полное изменение внутренней энергии равно нулю.
. В частности, если система возвращается в результате какого-либо перехода в исходное состояние, то полное изменение внутренней энергии равно нулю.
Подобно потенциальной энергии в механике,  определяется с точностью до постоянной величины
определяется с точностью до постоянной величины 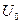 , зависящей от выбора отсчета внутренней энергии, т.е., от выбора нуля. Так, как во всех расчетах термодинамики находят не абсолютное значение внутренней энергии, а ее изменение
, зависящей от выбора отсчета внутренней энергии, т.е., от выбора нуля. Так, как во всех расчетах термодинамики находят не абсолютное значение внутренней энергии, а ее изменение 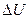 , то выбор
, то выбор 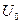 не играет роли.
не играет роли.
Составляющие внутренней энергии в) и г) не изменяются во всех процессах, не связанных с химическими реакциями и другими превращениями электронных оболочек атомов и ионов, а также ядерными реакциями и их можно не включать во внутреннюю энергию. Поэтому в дальнейшем под внутренней энергией в термодинамике будем понимать только сумму кинетической энергии теплового механического движения молекул и потенциальной энергии их взаимодействия. В идеальном газе последнее слагаемое равно нулю, значит его внутренняя энергия равна сумме кинетических энергий беспорядочного движения всех молекул.
Б-5
1. Закон инерции. Инерциальные системы отсчета.
2. Малые колебания. Диф. уравнение незатухающих колебаний и его решение.
3. Работа и теплота как два способа обмена энергией между термодинамической системой и внешними телами.
1. Закон инерции.
В основе классической механики лежит три закона Ньютона, сформулированные в сочинении «???», опубликованном в 1687г. Эти законы явились результатом гениального обобщения опытных данных и теоретических закономерностей в области механики, которые были установлены Ньютоном, а также Кеплером. Галилеем, Гюйгенсом. Гуком и др.
В качестве 1 закона динамики Ньютон принял закон, установленный еще Галилеем: Всякое тело сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока внешнее воздействие не заставит изменить это состояние.
Этот закон утверждает, что для состояния покоя или равномерно-прямолинейного движения не требуется внешних воздействий. В этом проявляется особое динамическое свойство тел, называемое инертностью. Поэтому 1 закон Ньютона называют законом инерции, а движение тела в отсутствии внешних воздействий, движение по инерции.
В этом законе считается, что тело не деформируется, т.е. оно абсолютно твердое, и что оно движется поступательно. Однако, твердое тело может еще вращаться по инерции. Необходимость во всех этих оговорках отпадает, если в законе Ньютона говорить не о теле, а о материальной точке, которая по определению не может ни деформироваться, ни вращаться.
Поэтому лучше пользоваться формулировкой:
материальная точка сохраняет состояние покоя или равномерно-прямолинейного движения до тех пор пока внешнее воздействие не выведет её из этого состояния.
Инерциальная система отсчета.
Известно что механическое движение относительно и его характер зависит от выбора системы отсчета. Первый закон выполняется не во всех системах отсчета. Например, тела, лежащие на гладком полу поезда, который идет равномерно и прямолинейно, могут прийти в движение относительно поезда по полу без всякого воздействия на них со стороны других тел. Для этого достаточно, чтобы поезд начал менять скорость хода, т.е. начал двигаться с ускорением.
Системы отсчета, по отношению к которым выполняется закон инерции, называются инерциальными системами отсчета.
Если бы такие системы нельзя было указать, то I-ый закон потерял бы смысл. Следовательно в I-ом законе имеется два утверждения: во-первых всем телам присуще свойство инертности, во-вторых можно указать системы отсчета, являющиеся инерционными.
Инерционной системой отсчета называют систему, в которой свободная от внешних воздействий материальная точка имеет равное нулю ускорение относительно нее, т.е. движется по инерции. Поэтому любые две инерционные системы отсчета либо неподвижны ??? либо движутся равномерно и прямолинейно.
Из опытов известно, что с большой степенью точности можно назвать инерционным гелиоцентр системы отсчета. Начало координат – в центре масс (практически в центре Солнца), а оси взаимно 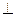 и направлены ????. Земная система отсчета неинерциальная из-за суточного вращения Земли, однако это вращение медленное, поэтому в большинстве практических задач, эффекты связанные с вращением Земли являются малыми и их можно не учитывать, И Землю также можно считать инерциальной системой отсчета.
и направлены ????. Земная система отсчета неинерциальная из-за суточного вращения Земли, однако это вращение медленное, поэтому в большинстве практических задач, эффекты связанные с вращением Земли являются малыми и их можно не учитывать, И Землю также можно считать инерциальной системой отсчета.
Существует бесчисленное множество инерционных систем отсчета движущихся относительно друг друга прямолинейно и равномерно. Системы отсчета которые движутся с ускорением называются неинерциальными.
3. Работа и теплота
Обмен энергией между т.системой и внешними телами может происходить двумя качественно различными способами: путем совершения работы и путем теплопередачи. Первый способ, как известно из механики, осуществляется при силовом взаимодействии между телами. Энергия, передаваемая при этом т. системе внешними телами, называется работой, совершаемой над системой
Энергия, передаваемая внешними телами путем теплообмена, называется теплотой, получаемой т. системой от внешней среды.
Для совершения работы над неподвижной системой необходимо, чтобы перемещались внешние тела, т.е., чтобы изменялись внешние параметры состояния системы.
В отсутствии внешних силовых полей обмен энергией между неподвижной системой и внешней средой путем совершения работы происходит только при изменении объема и формы системы. Например, работу над газом производят силы давления на газ со стороны внешней среды. При этом работа внешних сил над системой 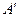 , численно равна и противоположна по знаку работе
, численно равна и противоположна по знаку работе 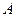 , совершаемой самой системой над внешней средой, т.е., против внешних сил.
, совершаемой самой системой над внешней средой, т.е., против внешних сил.
В отличие от внутренней энергии системы, являющейся однозначной функцией состояния этой системы, понятие теплоты и работы имеют смысл только в связи с видом процесса изменения состояния системы. Они являются энергетическими характеристиками конкретного процесса.
Существует качественное различие между совершением работы и теплообменом, как способами обмена энергией между макросистемами. Совершение работы над системой может изменить любой вид энергии системы. Например, при неупругом соударении тел часть совершенной работы идет на изменение кинетической энергии, а часть работы – на приращение внутренней энергии. Если же энергия сообщается в виде теплоты, то она идет только на увеличение энергии теплового движения молекул, т.е. на 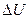 .
.
Б-6
1. Сила. Масса тела.
2. Центробежная сила инерции.
3. Первый закон термодинамики.
1. Сила. Ньютоновское определение.
Сила — мера механического воздействия одного тела на другое, векторная величина. Взаимодействие может осуществляться непосредственно в контакте или между удаленными телами, с помощью физических полей: гравитационное, электромагнитное. Сила задана, если указаны её модуль, направление и точка приложения.
Из опытов следует что действие нескольких сил на тело которые приложены в одной точке можно заменить действием одной силы, равной их геометрической сумме 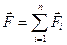 . Приложенной в той же точке называется результирующей. В основ механического явления лежат гравитационное и электромагнитное взаимодействия. Однако, для практических задач вводят следующие силы:
. Приложенной в той же точке называется результирующей. В основ механического явления лежат гравитационное и электромагнитное взаимодействия. Однако, для практических задач вводят следующие силы:
1. Сила тяжести 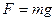 ;
;
2. Упругости сила 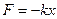 ;
;
3. Сила трения 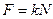 ;
;
4. Сила сопротивления среды  ;
;
2.5. Масса. 2-ой закон Ньютона.
Основная задача механики заключается в определении характеристик движения тел под действием приложенных к ним сил. Из опыта известно, что под действием силы 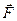 свободное твердое тело изменяет свою скорость, приобретая ускорение
свободное твердое тело изменяет свою скорость, приобретая ускорение 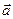 , это ускорение пропорционально силе и совпадает с ней по направлению.
, это ускорение пропорционально силе и совпадает с ней по направлению.
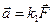 (*)
(*)
где  — коэффициент пропорциональности;
— коэффициент пропорциональности; 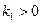 , постоянный для каждого конкретного тела, разный для разных тел. Это соотношение(*) отражает свойство инертности тел, согласно которому тела изменяют скорость не мгновенно, а постепенно, приобретая под действие
, постоянный для каждого конкретного тела, разный для разных тел. Это соотношение(*) отражает свойство инертности тел, согласно которому тела изменяют скорость не мгновенно, а постепенно, приобретая под действие 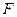 конечное ускорение.
конечное ускорение.
В качестве меры инертности в механике вводится положительная величина 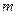 —масса тела. Чем больше инертность, а следовательно, его масса, тем меньше
—масса тела. Чем больше инертность, а следовательно, его масса, тем меньше 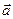 оно должно приобретаться под действием одной и той же силы. Поэтому приняв в (*)
оно должно приобретаться под действием одной и той же силы. Поэтому приняв в (*) 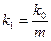 ;
; 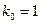 во всех системах ??? получим:
во всех системах ??? получим:
 — второй закон Ньютона;
— второй закон Ньютона;
Отсюда следует, что 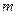 величина постоянная для данного тела (по Ньютону масса количество материи), не зависящая от состояния движения тела. Ни от его положения в пространстве, ни от действия других тел. Поэтому для сравнения масс двух тел достаточно сравнить ускорения
величина постоянная для данного тела (по Ньютону масса количество материи), не зависящая от состояния движения тела. Ни от его положения в пространстве, ни от действия других тел. Поэтому для сравнения масс двух тел достаточно сравнить ускорения  , приобретенные ими под действием одинаковой силы;
, приобретенные ими под действием одинаковой силы;
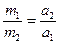 ;
;
Из опыта следует, что масса величина аддитивная, т.е. масса тела равна сумме масс всех составляющих его частей. Масса произвольной механической системы равна сумме масс материальных точек, на которые эту систему можно разбить.
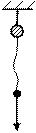 Обычно массу тела определяют сравнением её с массой эталонных тел (гирь) путем взвешивания на рычажных весах. Этот метод основывается на том, что в одной и той же точке земного шара все тела падают с одним ускорением
Обычно массу тела определяют сравнением её с массой эталонных тел (гирь) путем взвешивания на рычажных весах. Этот метод основывается на том, что в одной и той же точке земного шара все тела падают с одним ускорением  . Свободное падение обусловлено действием единственной силы—силы тяжести
. Свободное падение обусловлено действием единственной силы—силы тяжести  , так что согласно (*):
, так что согласно (*):
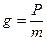 ;
;
и отношение масс:
|
 ;
;
Инертность можно продемонстрировать: скатерть из-под накрытого стола, вертикальный шарик на нити тянуть за нитку.
3. Первый закон термодинамики
Равновесный процесс перехода т. системы из начального состояния 1 в другое – 2 можно рассмотреть с точки зрения закона сохранения энергии. Изменение внутренней энергии системы 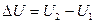 в таком процессе равно сумме работы, совершенной внешними силами над системой
в таком процессе равно сумме работы, совершенной внешними силами над системой 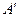 и теплоты, сообщенной системе,
и теплоты, сообщенной системе, 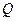 :
:
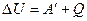 .
.
Работа 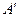 численно равна и противоположна по знаку работе
численно равна и противоположна по знаку работе 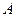 , совершаемой самой системой против внешних сил в том же равновесном переходе:
, совершаемой самой системой против внешних сил в том же равновесном переходе: 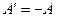 , тогда первый закон термодинамики можно записать в виде:
, тогда первый закон термодинамики можно записать в виде:
 ,
,
т.е., теплота, сообщенная системе, идет на приращение внутренней энергии и на совершение системой работы над внешними телами.
Обычно первый закон записывают для изменения состояния системы при сообщении ей малого количества теплоты , совершением системой малой (элементарной) работы
, совершением системой малой (элементарной) работы 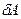 и элементарному изменению (приращению) внутренней энергии
и элементарному изменению (приращению) внутренней энергии  :
:
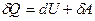
Отличие в записи малых величин теплоты и работы и изменении внутренней энергии не формальны, а отражают глубокое физическое различие этих величин. Дело в том, что внутренняя энергия системы является однозначной функцией ее состояния. Ее значение в каком-либо произвольном состоянии не зависит от того, каким способом система пришла в это состояние, 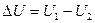 . При совершении системой процесса, в результате которого она вновь возвращается в исходное состояние, полное изменение энергии
. При совершении системой процесса, в результате которого она вновь возвращается в исходное состояние, полное изменение энергии  , т.е., интеграл:
, т.е., интеграл:
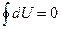
Это тождество является необходимым и достаточным условием для того, чтобы выражение  представляло собой полный дифференциал. Ни работа, ни теплота не являются функциями состояния и поэтому
представляло собой полный дифференциал. Ни работа, ни теплота не являются функциями состояния и поэтому 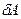 и
и  не являются полными дифференциалами. По определению из математики полный дифференциал функции:
не являются полными дифференциалами. По определению из математики полный дифференциал функции:
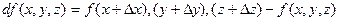 , т.е., определяется значениями функции в конечном и начальном состояниях и не зависит от пути перехода.
, т.е., определяется значениями функции в конечном и начальном состояниях и не зависит от пути перехода.
Все физические величины, входящие в 1 закон термодинамики могут быть больше нуля или меньше нуля, возможно также, что  = 0 и
= 0 и 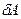 = 0. Если теплота подводится,
= 0. Если теплота подводится,  >0, если отводится, то
>0, если отводится, то  < 0. На одних участках перехода она может быть положительна, на других – отрицательна.
< 0. На одних участках перехода она может быть положительна, на других – отрицательна.
Общее количество теплоты, сообщенное системе в конечном процессе перехода 1 – 2 равно алгебраической сумме теплот  , сообщенных на всех участках процесса:
, сообщенных на всех участках процесса:
 .
.
Работа, совершаемая системой в конечном процессе 1 – 2 равна алгебраической сумме работ 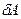 , т.е.,
, т.е.,
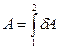
Изменение внутренней энергии в этом конечном переходе:
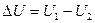 и не зависит от вида перехода.
и не зависит от вида перехода.
Б-7
1. Основное уравнение динамики материальной точки. Элементарный импульс силы и импульс силы.
2. Сила Кориолиса.
3. Работа идеального газа при расширении.
1. Основной закон динамики материальной точки.
Уравнение  описывает изменение движения протяженного тела под действием силы при отсутствии деформации и оно движется. Для точки оно справедливо всегда. поэтому его можно рассматривать как основной закон движения материальной точки: ускорение материальной точки пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки. В механике Ньютона масса не зависит от характеристик движения,
описывает изменение движения протяженного тела под действием силы при отсутствии деформации и оно движется. Для точки оно справедливо всегда. поэтому его можно рассматривать как основной закон движения материальной точки: ускорение материальной точки пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки. В механике Ньютона масса не зависит от характеристик движения, 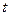 ,
, 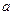 ускорение
ускорение 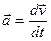 ;
; 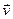 —скорость точки, тогда
—скорость точки, тогда  или
или
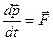 (**).
(**).
Вектор  называют импульсом материальной точки. В теоретической механике(а раньше и в физике) вектор
называют импульсом материальной точки. В теоретической механике(а раньше и в физике) вектор  называют количеством движения. Импульс одна из важнейших динамических характеристик материальной точки
называют количеством движения. Импульс одна из важнейших динамических характеристик материальной точки
В форме (**) основной закон динамики материальной точки утверждает, что скорость изменения импульса материальной точки равна действующей на нее силе. В этом состоит (согласно современной терминологии) второй закон Ньютона.
Основной закон динамики материальной точки выражает принцип причин в классической механике, т.к. устанавливает однозначную связь между изменением со временем состояния движения и положения материальной точки в пространстве и действия на нее силы. Закон позволяет по начальному состоянию точки (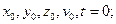 ) и действующей силы рассчитать состояние материальной точки в любой последующий момент времени.
) и действующей силы рассчитать состояние материальной точки в любой последующий момент времени.
На основании обобщения опытных фактов был установлен важный принцип независимости действия сил: если на материальную точку одновременно действует несколько сил, то каждая из них, сообщает материальной точке такое же ускорение, как если бы других сил не было. Т.о.
 ;
; 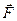 —результирующая сила;
—результирующая сила;
Основной закон можно переписать в виде:
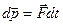 ;
;
вектор 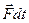 называется элементарным импульсом силы за малый промежуток времени
называется элементарным импульсом силы за малый промежуток времени 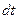 её действия. Т.о. из основного закона и принципа независимости действия сил следует, что изменение импульса материальной точки за малый промежуток времени
её действия. Т.о. из основного закона и принципа независимости действия сил следует, что изменение импульса материальной точки за малый промежуток времени 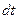 равно элементарному импульсу результирующих всех сил, действующих на эту точку за тот же
равно элементарному импульсу результирующих всех сил, действующих на эту точку за тот же 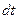 .
.
 Изменение импульса за конечный промежуток времени от
Изменение импульса за конечный промежуток времени от  до
до 
|
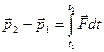 —импульс силы;
—импульс силы;
если 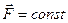 то
то  ,
, 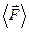 среднее значение силы за
среднее значение силы за 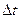 .
.
3. Работа при расширении или сжатии газа
Найдем работу, которая совершается при расширении или сжатии газа, заключенного в сосуде с подвижным поршнем площадью 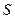 . Внешняя сила, действующая на поршень
. Внешняя сила, действующая на поршень 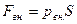 . При перемещении поршня вверх на малое расстояние
. При перемещении поршня вверх на малое расстояние 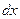 газ совершает элементарную работу
газ совершает элементарную работу 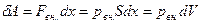 , где
, где 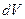 - изменение объема газа. Если изменение объема происходит квазистатически, то в любой момент времени газ находится в равновесном состоянии с внешней средой и его давление
- изменение объема газа. Если изменение объема происходит квазистатически, то в любой момент времени газ находится в равновесном состоянии с внешней средой и его давление 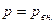 Элементарная работа газа в равновесном (квазистатическом) процессе изменения его объема:
Элементарная работа газа в равновесном (квазистатическом) процессе изменения его объема: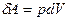 . Т.к.,
. Т.к., 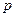 > 0, то при расширении газ совершает положительную работу. При сжатии
> 0, то при расширении газ совершает положительную работу. При сжатии 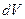 < 0, значит,
< 0, значит, 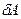 < 0 – работа газа отрицательна, положительную работу в этом случае совершают внешние силы.
< 0 – работа газа отрицательна, положительную работу в этом случае совершают внешние силы.
Если давление постоянное, то работа 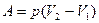 , при
, при 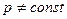 работа вычисляется как сумма элементарных работ, т.е., путем интегрирования:
работа вычисляется как сумма элементарных работ, т.е., путем интегрирования:
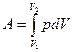 . Это численно равно площади под кривой
. Это численно равно площади под кривой 
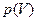 на соответствующем графике, рис. Эти выражения справедливы при любых изменениях объема твердых, жидких и газообразных тел.
на соответствующем графике, рис. Эти выражения справедливы при любых изменениях объема твердых, жидких и газообразных тел.
Б-8
1. Третий закон Ньютона.
2. Гармонические колебания. Уравнение гармонических колебаний.
Потенциальная и кинетическая энергия колебаний.
3. Изопроцессы идеального газа: изохорный.
1. наблюдения и опыты свидетельствуют, что механическое действие тел одного на другое всегда является взаимодействием. Если тело 2 действует на тело 1, то тело 1 обязательно действует на тело 2. на ведущие колеса автомобиля со стороны шоссе действует сила трения покоя в сторону движения автомобиля, а колеса действуют на шоссе с силами трения покоя в противоположные стороны.
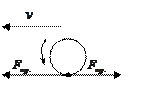 Количественное описание механического взаимодействия было дано Ньютоном в его III-ем законе динамики.
Количественное описание механического взаимодействия было дано Ньютоном в его III-ем законе динамики.
Действию всегда есть равное и противоположное противодействие, взаимодействия двух тел друг на друга равны между собой и направлены в противоположные стороны.
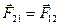
для точек: две материальные точки действуют друг на друга с силами равными по величине, направленные в противоположные стороны вдоль линий их соединения.
3. Уравнение первого закона термодинамики можно записать для равновесных процессов изменения его состояния в ином виде, используя выражения для теплоемкости однородного тела, откуда 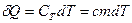 или с учетом молярной теплоемкости:
или с учетом молярной теплоемкости: 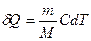 , а для одного моля
, а для одного моля  .
.
Тогда первый закон можно записать в виде:

Применим его к различным изопроцессам идеального газа.
Изохорный процесс, 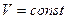 .(закон Шарля).
.(закон Шарля).
На диаграмме 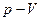 это вертикальная прямая: 1 – 2 нагрев , а 1 - 3 охлаждение. Практически этот процесс проводят, изменяя температуру газа, находящегося в толстостенном сосуде с неизменным объемом. В этом процессе работа не совершается:
это вертикальная прямая: 1 – 2 нагрев , а 1 - 3 охлаждение. Практически этот процесс проводят, изменяя температуру газа, находящегося в толстостенном сосуде с неизменным объемом. В этом процессе работа не совершается: 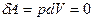 . Вся теплота идет на изменение его внутренней энергии.
. Вся теплота идет на изменение его внутренней энергии.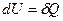 ,
,
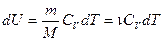 (1), где
(1), где 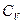 - молярная теплоемкость при постоянном объеме. Из опытов известно, что
- молярная теплоемкость при постоянном объеме. Из опытов известно, что 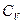 зависит от химического состава газа и его Т. Для не очень широкой области температур можно считать, что
зависит от химического состава газа и его Т. Для не очень широкой области температур можно считать, что 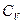 =const.
=const.
При изохорном конечном нагреве газа от температуры Т1 до температуры Т2 изменение внутренней энергии равно
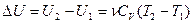 (2), и теплота, сообщенная системе:
(2), и теплота, сообщенная системе:
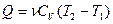 (3)
(3)
Для идеального газа внутренняя энергия это энергия теплового движения молекул, непосредственно не зависящая от объема (расстояния между молекулами), как в реальных газах. При расширении и сжатии газа его  будет изменяться только за счет изменения кинетической энергии теплового движения, т.е., за счет температуры. Таким образом, соотношения (1) и (2) справедливы для любого процесса изменения состояния идеального газа, а не только изохорного. Внутренняя энергия газа зависит только от его массы, химического состава и температуры. Это подтверждается опытами Гей – Люссака и Джоуля.
будет изменяться только за счет изменения кинетической энергии теплового движения, т.е., за счет температуры. Таким образом, соотношения (1) и (2) справедливы для любого процесса изменения состояния идеального газа, а не только изохорного. Внутренняя энергия газа зависит только от его массы, химического состава и температуры. Это подтверждается опытами Гей – Люссака и Джоуля.
Значит, для любого равновесного процесса изменения состояния идеального газа уравнение первого закона термодинамики имеет вид:
 (4)
(4)
Б-9
1. Затухающие колебания. Период колебаний. Добротность.
2. Принцип относительности Галилея.
3. Изопроцессы идеального газа: изобарный.
2. Принцип относительности Галилея
Значит ускорение какого-либо тела во всех системах отсчета, движущихся друг относительно друга прямолинейно и равномерно одинаково. Тогда если одна из систем инерциальная, то другая также будет инерциальная 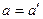 .
.
А значит и силы действующие на тела в разных инерциальных системах одинаковы. Масса в Ньютоновской механике также одинакова во всех системах отсчета. Из сказанного следует вывод, что уравнение динамики 
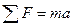 не изменяется при переходе от одной инерциальной системы отсчета к другой или как говорят они инвариантны по отношению к преобразованию координат, соответствующему переходу от одной инерциальной системы отсчета к другой. Это значит что, с механической точки зрения все инерциальные системы отсчета эквивалентны, ни одной из них нельзя отдать предпочтение перед другими. Практически ни какими опытами нельзя установить находится ли данная ИСО в покое или движется равномерно и прямолинейно. Находясь, например, в вагоне поезда, движущегося равномерно и прямолинейно нельзя установить (не выглянув в окно) движется ли он или находится в состоянии покоя. Мяч в вагоне поезда получит такое же ускорение, как и на Земле при действии одинаковой силы. Свободное падение тел и другие механические процессы будут происходить в вагоне также как если бы он покоился. подобное наблюдение и опыты проводил еще Галилей, поэтому положение о том, что все механические явления в разных ИСО протекают одинаковым образом это называется принципом относительности Галилея.
не изменяется при переходе от одной инерциальной системы отсчета к другой или как говорят они инвариантны по отношению к преобразованию координат, соответствующему переходу от одной инерциальной системы отсчета к другой. Это значит что, с механической точки зрения все инерциальные системы отсчета эквивалентны, ни одной из них нельзя отдать предпочтение перед другими. Практически ни какими опытами нельзя установить находится ли данная ИСО в покое или движется равномерно и прямолинейно. Находясь, например, в вагоне поезда, движущегося равномерно и прямолинейно нельзя установить (не выглянув в окно) движется ли он или находится в состоянии покоя. Мяч в вагоне поезда получит такое же ускорение, как и на Земле при действии одинаковой силы. Свободное падение тел и другие механические процессы будут происходить в вагоне также как если бы он покоился. подобное наблюдение и опыты проводил еще Галилей, поэтому положение о том, что все механические явления в разных ИСО протекают одинаковым образом это называется принципом относительности Галилея.
3. Изобарный процесс, 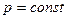 . ( Закон Гей -Люссака)
. ( Закон Гей -Люссака)
Он реализуется при нагревании газа в цилиндре с подвижным поршнем, на который действует постоянное внешнее давление.
На рис. изображены процессы изобарного расширения газа при его нагревании (1-2) и изобарного сжатия при его охлаждении (2-3).
Элементарная теплота, сообщенная газу в изобарном процессе:
 (5), где
(5), где  - молярная теплоемкость при постоянном давлении.
- молярная теплоемкость при постоянном давлении.
Элементарная работа, совершенная идеальным газом при этом:
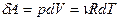 (6), учитывая уравнение Менделеева –Клапейрона.
(6), учитывая уравнение Менделеева –Клапейрона.
Из последнего уравнения можно выяснить смысл  :
:
 , т.е. универсальная газовая постоянная численно равна работе, совершенной одним молем идеального газа при его изобарном нагревании на 1К.
, т.е. универсальная газовая постоянная численно равна работе, совершенной одним молем идеального газа при его изобарном нагревании на 1К.
Подставим в первый закон выражения для  и
и 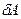 и найдем связь между
и найдем связь между 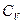 и
и  :
:
 , откуда:
, откуда: 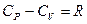 (7) – уравнение Майера для молярных теплоемкостей. Отсюда видно, что при изобарном нагревании газа к нему должна быть подведена большая теплота, чем для такого же изохорного нагревания, разность их равна работе, совершенной газом при изобарном расширении.
(7) – уравнение Майера для молярных теплоемкостей. Отсюда видно, что при изобарном нагревании газа к нему должна быть подведена большая теплота, чем для такого же изохорного нагревания, разность их равна работе, совершенной газом при изобарном расширении.
Работа газа при изобарном расширении при переходе из состояния 1 в состояние 2 , рис.
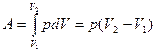 (8).
(8).
Если  постоянная, то теплота, сообщенная газу в изобарном процессе:
постоянная, то теплота, сообщенная газу в изобарном процессе:
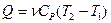 (9), а изменение внутренней энергии в процессе:
(9), а изменение внутренней энергии в процессе:
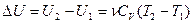 (10).
(10).
Б-10
1. Преобразования Галилея.
2. Вынужденные колебания.
3. Изопроцессы идеального газа: изотермический.
3. Изотермический процесс, Т=const. (закон Бойля – Мариотта)
Может происходить в условиях, когда теплообмен между газом и внешней средой осуществляется при постоянной (конечной) разности температур. Для этого теплоемкость внешней среды должна быть велика и процесс расширения или сжатия должен идти весьма медленно (для квазиравновесия). Изотермическими являются процессы кипения, конденсации, плавления и кристаллизации химически чистых веществ, происходящих при постоянном давлении.
Для идеального газа в этом процессе выполняется закон Бойля – Мариотта:  , графиком которого является гипербола, рис. . Внутренняя энергия газа постоянна в процессе, значит:
, графиком которого является гипербола, рис. . Внутренняя энергия газа постоянна в процессе, значит:
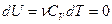 (11) , а
(11) , а 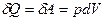 ,
,
т.е., вся теплота, сообщенная системе, идет на совершение газом работы против внешних сил:
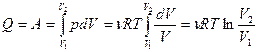 (12)
(12)
При изотермическом расширении 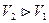 , к нему подводится теплота
, к нему подводится теплота 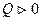 , газ совершает положительную работу,
, газ совершает положительную работу, 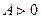 , рис. , процесс 1-2. При сжатии газа, процесс 1-3, работа, совершенная газом отрицательна, положительную работу при этом выполняют внешние силы, От газа отводится теплота
, рис. , процесс 1-2. При сжатии газа, процесс 1-3, работа, совершенная газом отрицательна, положительную работу при этом выполняют внешние силы, От газа отводится теплота  .
.
Теплоемкость газа в изотермическом процессе 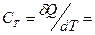 ±µ, т.к.,
±µ, т.к.,  .
.
Б-11
1. Закон сохранения импульса системы.
2. Резонанс.
3. Изопроцессы идеального газа: адиабатный.
1. . Закон сохранения импульса системы.
Импульсом тела или материальной точки является произведение,  т.е. вектор. Если взять замкнуть или изолировать систему тел или точек, то импульс такой системы будет равен геометрической сумме импульсов точек, составляющих систему
т.е. вектор. Если взять замкнуть или изолировать систему тел или точек, то импульс такой системы будет равен геометрической сумме импульсов точек, составляющих систему
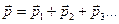 .
.
Импульс является одной из важнейших физических категорий (величин) по той причине, что в замкнутой системе он (вектор 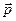 ) не изменяется, какие бы движения не происходили внутри системы. Это положение носит название закона сохранения импульса.
) не изменяется, какие бы движения не происходили внутри системы. Это положение носит название закона сохранения импульса.
Закон сохранения импульса следует непосредственно из законов Ньютона. Для каждого из тел замкнутой системы можно записать основной закон
 или
или 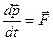 ;
;
Если записать это уравнение для первого тела, то в правой части будет стоять сумма сил, действующих на него со стороны остальных тел: 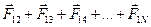 ; для второго
; для второго
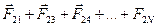 ;
;
И так далее или в общей форме т.е. для 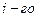 тела
тела
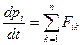 (
(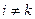 ),
),
а для всех тел
 (
(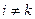 ).
).
По третьему закону Ньютона силы взаимодействия 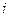 и
и 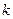 тел равны по величине и противоположны по направления
тел равны по величине и противоположны по направления 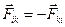 так, что
так, что  . Эти силы являются внутренними в системе и их сумма равна
. Эти силы являются внутренними в системе и их сумма равна 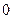 .
.
Левую часть по известному правилу дифференцирования суммы можно записать
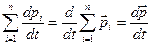 .
.
Т.о.
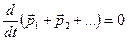 ; т.е.
; т.е. 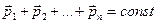 .
.
Т.е. величина и направление импульсов отдельных тел могут меняться, но их геометрическая сумма в замкнутой системе сохраняется. Если действуют внешние силы то
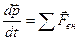 .
.
Т.е. можно сказать, что причина изменения импульса системы — действие внешних сил. Это справедливо. Разумеется, только по отношению к инерциальным системам отсчета.
Импульс может сохраняться и не у замкнутой системы, если результирующая внешних сил равна 0.
У незамкнутой системы может сохраняться не сам импульс 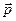 , а его проекция
, а его проекция 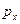 на некоторое направление
на некоторое направление  . Это бывает, если проекция результирующей силы на это направление
. Это бывает, если проекция результирующей силы на это направление 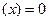 т.е.
т.е. 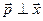 . Например, при движении системы в однородном поле сил тяжести сохраняется
. Например, при движении системы в однородном поле сил тяжести сохраняется 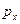 , что бы в системе не происходило.
, что бы в системе не происходило.
Подчеркнем, что закон сохранения импульса возможен только в инерциальной системе. Это не исключает случаев, когда 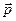 сохранялся бы и в неинерциальной системе отсчета. Для этого достаточно в уравнении
сохранялся бы и в неинерциальной системе отсчета. Для этого достаточно в уравнении  .
.  , которая включает и силы инерции была равна 0. это может выполняться при специальных условиях.
, которая включает и силы инерции была равна 0. это может выполняться при специальных условиях.
3. Адиабатный процесс, 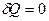 .
.
Это процесс, при котором система не обменивается теплотой с окружающей средой. Практически процесс производят при достаточно быстром расширении или сжатии газа.
Тогда из первого закона следует:
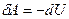 - система совершает работу за счет убыли внутренней энергии. Или, записывая более подробно, получим:
- система совершает работу за счет убыли внутренней энергии. Или, записывая более подробно, получим:
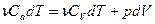 (13)
(13)
Здесь теплоемкость при адиабатном процессе -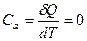 , т.к.,
, т.к., 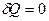 .
.
Из (13) видно, что 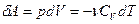 (14)
(14)
При расширении  и
и 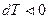 , газ охлаждается, при адиабатном сжатии
, газ охлаждается, при адиабатном сжатии 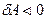 и
и 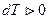 , газ нагревается.
, газ нагревается.
Связь между параметрами состояния адиабатного процесса можно найти, взяв дифференциалы от 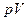 и от уравнения Менделеева - Клапейрона:
и от уравнения Менделеева - Клапейрона:
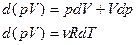 (15) , отсюда можно выразить
(15) , отсюда можно выразить  , подставить в уравнение (14) и получить:
, подставить в уравнение (14) и получить: 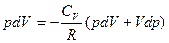 . Заменив здесь
. Заменив здесь  из уравнения Майера, получим после простых преобразований:
из уравнения Майера, получим после простых преобразований:
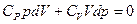 , далее разделим переменные, поделив уравнение на
, далее разделим переменные, поделив уравнение на 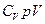 и обозначим
и обозначим 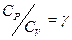 - показатель адиабаты или постоянная Пуассона.
- показатель адиабаты или постоянная Пуассона.
Тогда 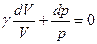 . После интегрирования
. После интегрирования  или:
или:
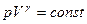
Это есть уравнение адиабаты или уравнение Пуассона. С помощью уравнения Менделеева – Клапейрона его можно записать через другие параметры:
 или
или 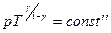 .
.
Из рис. видно, что адиабата идет круче, чем изотерма, поскольку 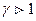 для любого идеального газа. Это объясняется тем, что при адиабатном сжатии увеличение давления происходит не только из-за уменьшения объема, как в изотермическом процессе, но и из-за возрастания температуры. При адиабатном расширении газа его температура уменьшается и давление падает сильнее, чем при соответствующем изотермическом расширении.
для любого идеального газа. Это объясняется тем, что при адиабатном сжатии увеличение давления происходит не только из-за уменьшения объема, как в изотермическом процессе, но и из-за возрастания температуры. При адиабатном расширении газа его температура уменьшается и давление падает сильнее, чем при соответствующем изотермическом расширении.
Работа в адиабатном (конечном) процессе 1-2 ( на рис. площадь под кривой)
Б-12
1. Энергия и работа. Элементарная работа и работа.
2. Распространение волн в упругой среде. Волновой фронт. Волновая поверхность.
3. Характер теплового движения молекул.
1. Энергия и робота
 Пусть частица под действием силы
Пусть частица под действием силы 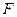 совершает перемещение по некоторой траектории 1-2. в общем случае сила
совершает перемещение по некоторой траектории 1-2. в общем случае сила 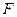 может меняться во времени по модулю, например, но не элементарном перемещении
может меняться во времени по модулю, например, но не элементарном перемещении 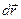 её можно считать
её можно считать 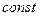 .
.
Действие силы на перемещении 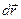 характеризуется физической величиной, равной скалярному произведению
характеризуется физической величиной, равной скалярному произведению  , которое называется элементарной работой силы
, которое называется элементарной работой силы 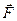 на перемещении
на перемещении 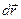 . Её можно ещё записать как
. Её можно ещё записать как  , где
, где 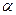 — угол между
— угол между 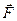 и
и 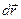
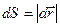 - элементарный путь
- элементарный путь 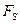 проекция вектора
проекция вектора 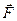 на вектор
на вектор 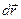
|
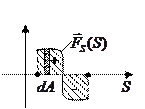 Значит элементарная работа
Значит элементарная работа  (*)
(*)
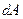 - величина алг. она и
- величина алг. она и 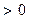 и
и  и = 0 при
и = 0 при  .
.
Суммируя ( интегрируя ) по всем элементарным участкам пути от 1 к 2 найдем работу силы 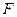 на данном пути.
на данном пути.
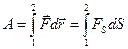 .
.
Геометрический смысл этого выражения виден из рисунка 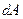 — полоска;
— полоска; 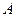 — площадь под прямой. Над осью работа положительна, под — отрицательна.
— площадь под прямой. Над осью работа положительна, под — отрицательна.
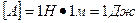 .
.
Найдем для примера работу некоторых центральных сил.
1. 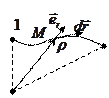
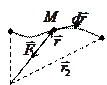
|
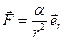 ;
;  —орт радиус вектора
—орт радиус вектора 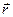 . Элементарная работа не ????
. Элементарная работа не ???? 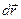 :
: 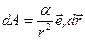 ;
; 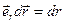 — приращение модуля вектора
— приращение модуля вектора 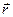 ;
; 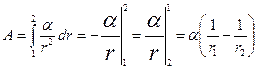 .
.
2. 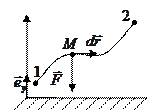
|
|
 ;
;  — радиус вектор частицы М относительно точки О. элементарная работа
— радиус вектор частицы М относительно точки О. элементарная работа  ;
;  .
.
3. Работа сил тяжести. 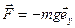 ;
;  ;
; 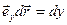 — приращение координаты
— приращение координаты 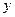 .
.

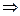

 ;
;  .
.
Работа всех этих сил не зависит от формы пути а только от положения точек 1,2. Эта особенность не всех сил. Силы трения не обладают таким свойством.
3. Характер теплового движения молекул
Если газ находится в равновесии, его молекулы движутся совершенно хаотически. Все направления движения равновероятны, ни одному из них не может быть отдано предпочтение, из-за этого молекулы будут равномерно распределены по объему. Скорости молекул могут быть самыми различными по величине. При каждом соударении с другой молекулой скорость данной молекулы может, как возрасти, так и уменьшиться с равной вероятностью. Изменение v молекулы происходит случайным образом. Скорость молекулы не может быть равной бесконечности, а также равной 0. Следовательно, очень малые и очень большие скорости молекул по сравнению со средней скоростью <v> маловероятны; скорости молекул группируются в основном вблизи некоторого наиболее вероятного значения скорости.
Например, линейный размер молекулы кислорода » 4 А, объем 10-23
см3 . При нормальных условиях на одну молекулу приходится объем » 0,4×10-19
см3. Т.е., молекулы встречаются редко, проходя путь » 1000А между столкновениями. Т.к. скорость молекул велика, примерно 500 м/с, столкновения происходят через 10-10 с. Удары о стенки сосуда ничего не меняют, т.к. скорость изменяется только по направлению.
Молекулы притягиваются, когда расстояние между ними имеет порядок их размеров. Значит, большую часть пути они движутся прямолинейно и равномерно. Время взаимодействия очень мало » 10-13 с, т.е., взаимодействие можно считать соударением. Большую часть «своей жизни» молекула проводит в свободном движении по инерции.
Хаотичность движения молекул наглядна, если взять сферу некоторого произвольного радиуса r с центром в т. О. Любая т. А на сфере определяет направление от О к А. След-но направление движ. мол. в нек. момент времени м.б. задан. точками на сфере. Равновероятность всех напр. приводит к тому, что точки, изображающие напр. движ. мол., распределяется по сфере с пост. плотностью, равной числу мол. N/4πr2. Соударения приводит к измен. направлений движ. мол., поэтому положение N точек на сфере неопред. меняются, однако плотность точек из-за хаотичности движ. остается пост.
Можно найти какое кол-во мол. движется в напр., близких к данному (А). Таким напр. соответствуют все точки элемента пов. ΔS в окрестности т.А. В пределах ΔS будет
(*) ΔNA = N(ΔS/4πr2) = NΔΩ/4πΔΩ тел угол, в кот. закл.напр.
Индекс А означает, что имеются ввиду мол. с направл. ≈ А. Направление ОА можно задать с помощью полярного угла θ и азимут угла φ отсчитываемых от напр. ОZ и плоск. Р0. Разделив dS/r2 получим элемент тел. угла, отвечающий инт. углов от θ до θ+dθ и от φ до φ+dφ
dΩ = sinθdθdφ
Две сферы с r и r+dr, два конуса с углами раствора θ и θ+dθ и две плоскости, образующие с Р0 углы φ и φ+dφ образуют в пр-ве прямоуг. параллелепипед с объемом
dV = dSdr = r2sinθdrdθdφ –
элемент объема в сферической сист. коорд. (объем, отвечающий приращению корд. r, θ, φ на dr, dθ, dφ)
Перейдя от дельт и диффер. в ф-ле (*) и подставив dΩ получим
dNv,φ = N(dΩvφ/4π) = Nsinθdθdφ/4π
Индексы указывают на то, что имеются в виду молекулы, напр. движ. которых отвечают интервалам углов от θ до θ+dθ и от φ до φ+dφ.
Б-13
1. Работа гравитационной силы, упругой силы и силы тяжести.
2. Уравнение плоской и сферической волн.
3. Средняя арифметическая скорость молекулы.
1. Энергия и робота
 Пусть частица под действием силы
Пусть частица под действием силы 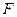 совершает перемещение по некоторой траектории 1-2. в общем случае сила
совершает перемещение по некоторой траектории 1-2. в общем случае сила 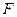 может меняться во времени по модулю, например, но не элементарном перемещении
может меняться во времени по модулю, например, но не элементарном перемещении 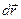 её можно считать
её можно считать 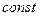 .
.
Действие силы на перемещении 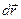 характеризуется физической величиной, равной скалярному произведению
характеризуется физической величиной, равной скалярному произведению  , которое называется элементарной работой силы
, которое называется элементарной работой силы 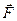 на перемещении
на перемещении 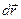 . Её можно ещё записать как
. Её можно ещё записать как  , где
, где 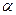 — угол между
— угол между 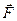 и
и 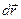
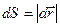 - элементарный путь
- элементарный путь 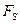 проекция вектора
проекция вектора 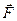 на вектор
на вектор 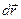
|
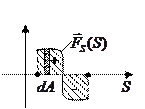 Значит элементарная работа
Значит элементарная работа  (*)
(*)
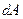 - величина алг. она и
- величина алг. она и 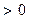 и
и  и = 0 при
и = 0 при  .
.
Суммируя ( интегрируя ) по всем элементарным участкам пути от 1 к 2 найдем работу силы 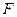 на данном пути.
на данном пути.
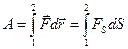 .
.
Геометрический смысл этого выражения виден из рисунка 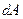 — полоска;
— полоска; 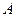 — площадь под прямой. Над осью работа положительна, под — отрицательна.
— площадь под прямой. Над осью работа положительна, под — отрицательна.
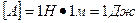 .
.
Найдем для примера работу некоторых центральных сил.
4. 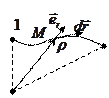
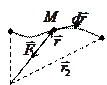
|
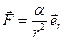 ;
;  —орт радиус вектора
—орт радиус вектора 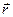 . Элементарная работа не ????
. Элементарная работа не ???? 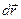 :
: 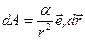 ;
; 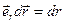 — приращение модуля вектора
— приращение модуля вектора 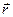 ;
; 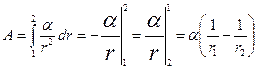 .
.
5. 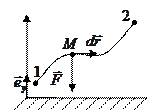
|
|
 ;
;  — радиус вектор частицы М относительно точки О. элементарная работа
— радиус вектор частицы М относительно точки О. элементарная работа  ;
;  .
.
6. Работа сил тяжести. 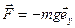 ;
;  ;
; 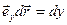 — приращение координаты
— приращение координаты 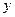 .
.

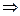

 ;
;  .
.
Работа всех этих сил не зависит от формы пути а только от положения точек 1,2. Эта особенность не всех сил. Силы трения не обладают таким свойством.
3. Средняя арифметическая скорость<v> по определению равна отношению суммы скоростей всех молекул единицы объема к числу молекул единицы объема.
Число молекул в единице объема dnv, скорости которых заключены в интервале от v до v+dv равно nf(v)dv; Сумма скоростей всех таких молекул равна vnf(v)dv. Чтобы найти сумму скоростей всех молекул, обладающих любыми скоростя
|
|
|
|
 <v> = 4/√π
<v> = 4/√π (m
(m /2kT)3/2∫ v3edv = 4/√π (m/2kT)3/2∫ v2evdv
/2kT)3/2∫ v3edv = 4/√π (m/2kT)3/2∫ v2evdv
vdv = d(v2)/2, значит <v> = 4/√π (m/2kT)3/2½∫ v2ed(v2)
Введем новую переменную Z=mv2/2kT : ½∫ v2ed(v2) = ½ (2kT/m)2∫Ze-ZdZ, тогда, учитывая, что ∫Ze-ZdZ =1, получим:
<v> = 4/√π (m/2kT)3/22(kT/m)2 = √8kT/πm
Б-14
1. Мощность.
2. Волновое уравнение.
3. Число ударов молекул о стенку и давление газа на стенку.
1. Мощность по определению это работа, выполненная за единицу времени. Если за промежуток времени 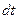 сила
сила 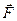 совершает работу
совершает работу 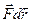 , то мощность, развиваемая этой силой в данный момент времени
, то мощность, развиваемая этой силой в данный момент времени  т.е. скалярное произведение
т.е. скалярное произведение 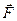 и
и 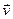 .
.
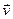 — скорость движения точки приложения силы.
— скорость движения точки приложения силы.
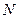 — как и работа величина алгебраическая.
— как и работа величина алгебраическая.
Зная 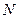 можно найти работу, которая совершает сила
можно найти работу, которая совершает сила 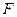 за время
за время 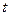
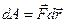
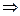

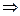

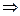

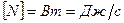 .
.
3. Число ударов молекул о стенку
Рассмотрим находящийся в равновесии газ, заключенный в некотором сосуде. Допустим, что молекулы газа движутся только вдоль трех взаимно ┴ направлений. Это можно допустить из-за хаотичности движения молекул. Если в сосуде находится N молекул, то в любой момент времени вдоль каждого из направлений будет двигаться N/3 молекул и половина из них - N/6 вдоль данного направления в одну сторону, а вторая половина - в другую. Следовательно, в интересующем нас направлении по нормали к данному элементу ΔS стенки сосуда движется N/6 молекул, а для единицы объема - 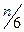 , n – концентрация молекул.
, n – концентрация молекул.
Пусть все молекулы движутся с одинаковой средней скоростью <v>. За время Δt элемента стенки ΔS достигают все молекулы, находящиеся в параллелипипеде с площадью основания ΔS и длиной  <v>Δt. Их число Δν = (n/6)ΔS<v>Δt, следовательно, число ударов о единичную площадку в единицу времени
<v>Δt. Их число Δν = (n/6)ΔS<v>Δt, следовательно, число ударов о единичную площадку в единицу времени
Δν/ΔSΔt = (n/6)<v>.
Если отказаться от допущения, что все молекулы движутся с одинаковой скоростью v = <v>, то необходимо выделить в единице объема молекулы, скорости которых лежат в интервале от v до v+dv. Их число - . Количество ударов таких молекул, долетающих до площадки ΔS за время Δt равно dνv = (1/6)(dnvΔ
. Количество ударов таких молекул, долетающих до площадки ΔS за время Δt равно dνv = (1/6)(dnvΔ
|
|
Δν = 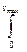 dνv = 1/6ΔSΔt
dνv = 1/6ΔSΔt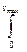 vdnv = Выражение
vdnv = Выражение 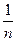
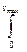 vdnvпо определению является средней скоростью молекулы, тогда Δν = 1/6ΔSΔtn<v> , т.е., получили то же самое значение числа ударов.
vdnvпо определению является средней скоростью молекулы, тогда Δν = 1/6ΔSΔtn<v> , т.е., получили то же самое значение числа ударов.
Давление газа на стенку сосуда
Давление по определению можно записать:  , а поскольку, из второго закона Ньютона:
, а поскольку, из второго закона Ньютона: 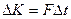 , то
, то  . Значит, необходимо вычислить импульс
. Значит, необходимо вычислить импульс 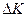 , передаваемый всеми молекулами со всеми скоростями единице площади за единицу времени.
, передаваемый всеми молекулами со всеми скоростями единице площади за единицу времени.
Число молекул со скоростью v из общего количества n, долетающих до площадки ΔS за время Δt равно:
dνv = (1/6)(dnvΔSvΔt)
Далее, умножив это число на импульс, сообщаемый каждой молекулой при ударе равный – 2mv, получим импульс, сообщаемый площадке ΔS за время Δt этими молекулами. Изменение импульса одной молекулы равно K2-K1= -2mv, значит, импульс передаваемый молекулой ст
|
|
равен 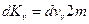 v.
v.
Импульс, передаваемый всеми молекулами со всеми скоростями:
 K =
K = 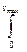 (1/6)(dnvΔSvΔt)2mv = 1/3 mΔSΔt
(1/6)(dnvΔSvΔt)2mv = 1/3 mΔSΔt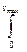 v2dnv (*)
v2dnv (*)
Выражение 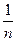
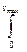 v2dnv представляет собой среднее значение квадрата скорости молекул, тогда, заменив в (*) интеграл и, разделив это выражение на ΔS и Δt, получим давление газа на стенку сосуда:
v2dnv представляет собой среднее значение квадрата скорости молекул, тогда, заменив в (*) интеграл и, разделив это выражение на ΔS и Δt, получим давление газа на стенку сосуда:
р = 1/3mn<v2>
т.к. m<v2>/2 = <εпост> по определению, получим:
р =2/3n<εпост>
- основное уравнение молекулярно- кинетической теории. Это уравнение раскрывает физический смысл макропараметра р: давление определяется средним значением кинетической энергии поступательного движения молекул.
Б-15
1. Консервативные силы.
2. Энергия волны. Объемная плотность энергии волны.
3. Средняя энергия молекул с учетом вращательных и колебательных степеней свободы.
1. Консервативные силы
Если в каждой точке пространства на частицу, помещенную туда, действует сила, говорят, что частица находится в поле сил, например в поле сил тяжести, гравитационной, кулоновской и т.д. Поле сил может быть постоянным во времени, тогда оно называется стационарным. Стационарное поле в одной системе отсчета м.б. в другой. В стационарном поле сила, действующая на частицу, зависит только от её положения в пространстве.
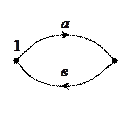 Работа, которую совершает сила поля по перемещению частиц из т.1 в т.2 зависит, в общем случае от формы пути между этими точками, например при действии
Работа, которую совершает сила поля по перемещению частиц из т.1 в т.2 зависит, в общем случае от формы пути между этими точками, например при действии  . Однако, имеются стационарные силовые поля, в которых работа над частицей силами поля не зависит от пути между т.1 и т.2. Силы обладающими такими свойствами называются консервативными. Это свойство можно сформулировать другим способом: силы поля являются консервативными, если работа в стационарном полена любом замкнутом пути равна =0.
. Однако, имеются стационарные силовые поля, в которых работа над частицей силами поля не зависит от пути между т.1 и т.2. Силы обладающими такими свойствами называются консервативными. Это свойство можно сформулировать другим способом: силы поля являются консервативными, если работа в стационарном полена любом замкнутом пути равна =0.
|
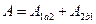 поскольку
поскольку  то
то 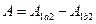 . А т.к. работа не зависит от пути
. А т.к. работа не зависит от пути 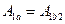 , то
, то  .
.
К неконсервативным силам относятся силы трения и сопротивления. Работа этих сил зависит от пути между начальным и конечным положением частицы и не равна 0 на замкнутом пути.
3. Средняя энергия молекул
Из уравнения состояния идеального газа p=nkT и выражения для давления газа на стенку сосуда р =2/3n<εпост> следует, что
<εпост> = 3/2kT (1), откуда можно заключить, что температура есть величина, прямо пропорциональная средней энергии поступательного движения молекул.
Поступательно движутся молекулы газа. Молекулы твердых и жидких тел совершают колебания вблизи положений равновесия.
Из выражения (1) видно, что <εпост> зависит только от Т и не зависит от массы молекулы.
Т.к., <εпост> = <mv2/2> = m<v2>/2, то из сравнения с выражением (1), получим: <v2> = 3kT/m а средняя квадратичная скорость:
vср.кв. = √<v2> = √3kT/m .
Можно представить <v2> = <v2x>+<v2y>+<v2z> = 3<v2x>, поскольку, все направления движения молекул равноправны, т.е., <v2x> = <v2y> = <v2z>, тогда:
<v2x> = 1/3<v2> = kT/m
Формула (1) определяет энергию поступательного движения молекул. Наряду с этим движением возможны также вращение молекул и колебания атомов, входящих в состав молекул. Например, для двухатомной жесткой молекулы это вращение вокруг двух взаимно перпендикулярных осей, проходящих через центр масс молекулы. Эти виды движения также связаны с запасом энергии молекулы. Ее полную энергию позволяет определить, устанавливаемое статистической физикой, положение о равнораспределении энергии по степеням свободы молекулы. Такую гипотезу впервые высказал Больцман.
Числом степеней свободы механической системы называется количество независимых величин, с помощью которых может быть задано ее положение. Положение материальной точки определяется в пространстве значением трех координат, она имеет три степени свободы. Одноатомной молекуле следует приписывать три степени свободы, двухатомной: в зависимости от характера связи между атомами – либо три поступательных и две вращательных (жесткая связь), т.е. всего пять степеней; либо n = 3+2+1=6 с учетом колебательной степени свободы для нежесткой молекулы.
Поскольку ни одна из поступательных степеней свободы не имеет преимущества перед остальными, на каждую из них приходится в среднем одинаковая энергия 1/2kT. Согласно закону равнораспределения на каждую степень свободы молекулы приходится в среднем одинаковая энергия, равная 1/2kT. Согласно закону среднее значение энергии одной молекулы <ε> будет тем больше, (при одинаковой Т), чем сложнее молекула и чем больше у нее степеней свободы. При определении <ε> необходимо учесть, что колебательная степень свободы обладает вдвое большей «энергетической емкостью» по сравнению с поступательной или вращательной. Это объясняется тем, что колебательное движение связано с наличием кинетической и потенциальной энергии, поэтому на колебательную степень приходится (1/2kT+1/2kT) = kT, т.е., одна половинка в виде εкин , а вторая - εпост.
Т.о. средняя энергия молекулы: <ε> = (i/2)(kT),
Где i- сумма поступательных, вращательных и удвоенного числа колебательных степеней свободы молекул.
i = nпост+nвращ+2nкол , здесь n – число степеней свободы.
Для молекул с жесткой связью i совпадает с числом степеней свободы.
Б-16
1. Центральные силы.
2. Пространство и время в ньютоновской механике.
3. Внутренняя энергия и теплоемкость CvиCp идеального газа.
1. . Центральные силы.
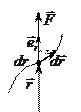 Всякое силовое поле вызвано действием определенных тел. Сила, действующая на частицу в этом поле обусловлена взаимодействием этой частицы с телами. Силы, которые зависят только от расстояния между взаимодействующими частицами и направлены вдоль прямой их соединяющей называются центральными (гравитационные, кулоновские, упругие). Центральные силы можно записать как
Всякое силовое поле вызвано действием определенных тел. Сила, действующая на частицу в этом поле обусловлена взаимодействием этой частицы с телами. Силы, которые зависят только от расстояния между взаимодействующими частицами и направлены вдоль прямой их соединяющей называются центральными (гравитационные, кулоновские, упругие). Центральные силы можно записать как 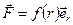
 зависит только от
зависит только от  ,
,  — орт
— орт 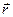 частицы
частицы 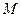 относительно О. докажем что центральная сила является консервативной. Для частицы
относительно О. докажем что центральная сила является консервативной. Для частицы 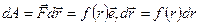 ;
; 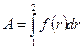 . Этот интеграл не зависит от формы пути, а зависит только от вида функции
. Этот интеграл не зависит от формы пути, а зависит только от вида функции  и от
и от 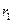 и
и 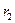 т.е. от пределов интегрирования. Если на частицу действует несколько центральных сил, то работа
т.е. от пределов интегрирования. Если на частицу действует несколько центральных сил, то работа 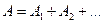 , а т.к. работа каждой из них не зависит от пути, то и
, а т.к. работа каждой из них не зависит от пути, то и 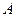 не зависит.
не зависит.
3. Внутренняя энергия и теплоемкость идеальных газов
В идеальном газе молекулы не взаимодействуют между собой, внутренняя энергия одного моля газа:
Uм = NA<ε> = i/2 NAkT = i/2 RT . Uм = i/2RT.
Если вспомнить, что по определению: Cv = δQ/dT = dU/dT, поскольку, δQ = dU+pdV, а для изохорного процесса dV = 0.
Тогда Cv = (i/2) R , а, учитывая, что Cр = Cv+R, получим:
Cр = (i+2)/2 R
Следовательно, коэффициент Пуассона γ = Cp/Cv = (i+2)/i , таким образом, γ определяется числом и характером степеней свободы молекулы.
Согласно этой ф-лы для одноатомной молекулы i = 3 и γ = 1,67; жесткой двухатомной i =5 и γ = 1,4; упругой двухатомной i = 7, а γ = 1,29. В области температур, близких к комнатной, это хорошо согласуется с опытом. Однако, в широком температурном интервале это не так. Оказывается, что вращательная и колебательная энергии молекулы квантованы. При низких Т вращательные и колебательные степени свободы не возбуждены. Молекула Н2 , например,ведет себя как одноатомная в этой области температур, i = 3. В области Т ≈ 500К вращательные степени «разморожены» <ε>>εвращ и молекула Н2 ведет себя как жесткая двухатомная с = 3+2 = 5. При Т>1000К энергии <ε> достаточно для возбуждения колебательной степени свободы, «включены» все степени свободы, i = 7.
Б-17
1. Потенциальная энергия частицы в поле.
2. Опыт Майкельсона и Морли.
3. Барометрическая формула.
1. Потенциальная энергия частицы в силовом поле.
То обстоятельство, что работа консервативной силы (для стационарного поля) зависит только от начального и конечного положений частицы в поле, позволяет ввести важное физическое понятие потенциальной энергии (функции состояния). Возьмем стационарное поле консервативных сил, например электростатическое поле в котором мы перемещаем частицу (заряд) из разных точек 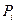 в некоторой фиксированной точке О (точка отсчета). Найдем работу сил поля. Поскольку работа сил поля не зависит от пути, то остаётся зависимость её только от положения т.
в некоторой фиксированной точке О (точка отсчета). Найдем работу сил поля. Поскольку работа сил поля не зависит от пути, то остаётся зависимость её только от положения т. (О— фиксировано) т.е. от предела интегрирования
(О— фиксировано) т.е. от предела интегрирования
|
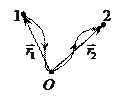
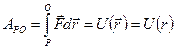 (*).
(*).
Это значит, что данная работа будет некоторой функцией радиус-вектора 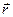 точки
точки 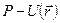 . Функцию
. Функцию  называют потенциальной энергией частицы в поле сил. Теперь найдем работу при перемещении частицы из т.1 в т.2. Т.к. она не зависит от формы пути: то
называют потенциальной энергией частицы в поле сил. Теперь найдем работу при перемещении частицы из т.1 в т.2. Т.к. она не зависит от формы пути: то  или с учетом (*)
или с учетом (*)
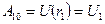 ;
;
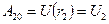 ;
;
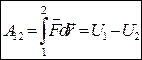 (**)
(**)
Правая часть представляет убыль потенциальной энергии, т.е. разность начальную и конечную значений потенциальной энергии. ( 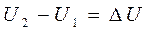 — приращение); (
— приращение); ( — убыль). Т.о. работа сил Оля на пути 1—2 равна убыли потенциальной энергии. Так как работа сил поля определяется лишь разностью энергий в двух точек, а не их абсолютного значения, то частица в т.О можно приписать любое, наперед выбранное значение потенциальной энергии.
— убыль). Т.о. работа сил Оля на пути 1—2 равна убыли потенциальной энергии. Так как работа сил поля определяется лишь разностью энергий в двух точек, а не их абсолютного значения, то частица в т.О можно приписать любое, наперед выбранное значение потенциальной энергии.
Однако, как только зафиксирована потенциальная энергия в одной, какой-либо точке, значения её во всех остальных точках поля определяется однозначно выражением (**). Эта формула позволяет найти вид 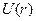 для любого стационарного поля консервативных сил. Для этого достаточно вычислить работу совершаемую силами поля между двумя любыми точками и представить её в виде убыли некоторой функции
для любого стационарного поля консервативных сил. Для этого достаточно вычислить работу совершаемую силами поля между двумя любыми точками и представить её в виде убыли некоторой функции 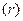 , которая и есть потенциальной энергией. Так и было ране сделано при вычислении работы гравитационной, упругой и силы тяжести. Отсюда видно, что потенциальная энергия частицы в данных полях имеет вид
, которая и есть потенциальной энергией. Так и было ране сделано при вычислении работы гравитационной, упругой и силы тяжести. Отсюда видно, что потенциальная энергия частицы в данных полях имеет вид

 — гравитационная, кулоновская +С – постоянная.
— гравитационная, кулоновская +С – постоянная.
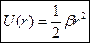 — упругой +С
— упругой +С
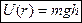 — в поле тяжести.
— в поле тяжести.
Отметим еще раз, что потенциальная энергия определяется с точностью до некоторой постоянной величины, что несущественно, т.к. во всех формулах входит разность её значения в двух положениях частицы, поэтому постоянная выпадает, и её опускают. Кроме этого важно заметить, что потенциальную энергию следует относить не к частице в поле а к системе взаимодействующих частиц и тела, создающего поле. При данном характере взаимодействия потенциальная энергия зависит только от положения частицы относительно этого тела.
3. Барометрическая формула
Атмосфера, то есть воздушная оболочка Земли, обязана своим существованиям наличию теплового движения молекул и силы притяжения их к Земле. При этом в атмосфере устанавливается вполне определенное распределение молекул по высоте. Соответственно этому, устанавливается определенный закон изменения давления воздуха с высотой, который нетрудно найти.
Возьмем вертикальный столб воздуха. Считаем, что при х=0, y поверхности Земли р=р0 , а на высоте х давление равно р. При увеличении высоты на dx давление уменьшается на dp. Известно, что давление воздуха на некоторой высоте равно весу вертикального столба воздуха с площадью равной единице, находящегося над этой высотой. Поэтому, dp равно разности весов столбов воздуха с площадью s=1 м2 на высотах x и x+dx, то есть, равно весу столба воздуха высотой dx с площадью основания 1 м2:
p-dp-p= -dp= ρgdx×1 м2, значит, dp= -ρgdx, плотность ρ= m0N/V= m0n, (m0N = m – масса всех молекул).
Из молекулярной физики известно, p= nkT =>n= p/kT =>ρ= m0p/kT
и тогда, подставляя значение плотности, получим: dp= (-m0g/kT)pdx. После разделения переменных: dp/p= (-m0g/kT)dx
Считая для простоты температуру постоянной на всех высотах (что не так) после интегрирования найдем:
lnp= (-m0g/kT)x +lnC , откуда: p= Ce(-m0g/kT)x . Постоянную C находим из начальных
условий: при х= 0 р= р0, то есть р0=C и тогда:
р= р0e(-m0g/kT)x
или с учетом m0= M/NA:р= р0e(-Mg/RT)x - барометрическая формула, т.е., давление с высотой убывает по экспоненциальному закону.
Для градуировки барометров необходимо внести поправки на Т. Так как, давление пропорционально концентрации молекул в единице объема, то: n= n0e(-mg/kT)x - закон убывания концентрации молекул, а значит, плотности с высотой.
Видно, что атмосфера Земли в принципе, простирается до ∞. На больших высотах необходимо учесть, что g – меняется с высотой: g(r)= γM/(r+x)2 .
Б-18
1.Связь между потенциальной энергией и силой для консервативного поля.
2.Постулаты Эйнштейна.
3. Распределение Больцмана.
1. Связь между потенциальной энергией и силой для консервативного поля.
Взаимодействие частицы с окружающими телами можно описать либо с помощью сил либо с помощью потенциальной энергией. Первый способ более общий , т.к. он применим и к силам, для которых нельзя ввести понятие потенциальной энергии (силы трения). Второй способ удобен тем, что существует связь между потенциальной энергией и силой со стороны поля. Зная эту связь, можно по виду зависимости 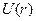 — функции положения частицы в поле, находить поле сил
— функции положения частицы в поле, находить поле сил 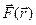 .
.
Найдем эту связь. Известно, что работа консервативных сил при перемещении частицы из одной точки статического поля в другую может быть представлена в виде убыли потенциальной энергии частицы 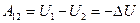 . Это можно записать и для элементарного перемещения
. Это можно записать и для элементарного перемещения 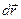 .
.

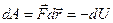
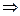
 т.к.
т.к. 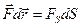 ;
; 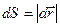 — элементарный путь или
— элементарный путь или 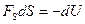 ;
; 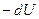 — убыль потенциальной энергии в направлении перемещения
— убыль потенциальной энергии в направлении перемещения 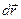 ; отсюда:
; отсюда:  т.е. проекция силы поля
т.е. проекция силы поля 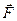 в данной точке на направление перемещения
в данной точке на направление перемещения 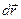 равна убыли потенциальной энергии в этом направлении. Символ
равна убыли потенциальной энергии в этом направлении. Символ  указывает, что произведение берется по определенному направлению. Перемещение
указывает, что произведение берется по определенному направлению. Перемещение 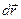 можно брать в любом направлении, например вдоль осей
можно брать в любом направлении, например вдоль осей  . Если вдоль
. Если вдоль  то
то 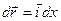 ; а
; а 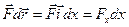 ,
, 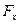 — проекция силы
— проекция силы 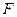 на орт
на орт 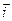 (а не на перемещение
(а не на перемещение 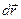 , как в случае
, как в случае 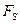 ). Т.о. относительно оси
). Т.о. относительно оси  можно записать
можно записать  . Символ
. Символ 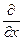 означает, что
означает, что 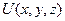 при дифференцировании должна расти как функция одного аргумента
при дифференцировании должна расти как функция одного аргумента  , а остальные аргументы —
, а остальные аргументы — 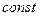 . Значит
. Значит 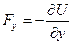 ;
;  . Зная проекции
. Зная проекции 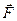 можно найти и сам вектор
можно найти и сам вектор 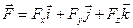 или
или 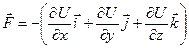 . Скобка называется градиент скалярной функции
. Скобка называется градиент скалярной функции  , и обозначается
, и обозначается 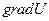 или
или 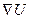 т.о.
т.о. 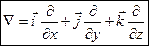 — символический вектор или оператор Гамильтона.
— символический вектор или оператор Гамильтона. 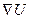 — формально можно рассматривать как произведение символического вектора
— формально можно рассматривать как произведение символического вектора  на скаляр
на скаляр  т.е. сила действующая со стороны поля на частицу равна со знаком минус градиент потенциальной энергии частицы в данной тоске поля. Т.о. зная
т.е. сила действующая со стороны поля на частицу равна со знаком минус градиент потенциальной энергии частицы в данной тоске поля. Т.о. зная 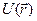 можно найти
можно найти 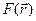 .
.
3. Распределение Больцмана
Барометрическая формула выражает зависимость концентрации молекул газа, находящегося в поле сил тяжести. Величина mgx представляет собой потенциальную энергию молекул на высоте х. Можно также сказать, что формула
n= n0e(-m0g/kT)x
дает нам число частиц n в единице объема, энергия которых равна m0gx, если концентрация частиц с энергией равной 0 равно n0 (отсчет х снизу).
Нет оснований считать, что поведение газа изменится, если вместо силы тяжести на него будет действовать какая либо другая сила, тогда для любого силового поля можно сказать,.что число частиц, имеющих заданную потенциальную энергию U, определяется формулой
n= n0e-U/kT – формула Больцмана
Она позволяет определить долю частиц, которые в условиях теплового равновесия обладают энергией U:
n/n0= e-U/kT
Отсюда видно, что доля n/n0 частиц с энергией U, т.е., их распределение по энергии определяется (кроме U) температурой. При данной Т доля молекул с той, либо иной энергией зависит от U и быстро уменьшается с ростом энергии. Доля молекул с большой энергией мала. И чем ниже Т, тем быстрее n/n0 убывает с ростом U, рис. . Чем выше температура, тем равнемернее распределен газ по объему.
Величина n/n0 в формуле имеет также смысл вероятности n молекул из всего числа n0 иметь заданную энергию U.
Б-19
1. Кинетическая энергия.
2. Замедление времени.
3. Функция распределения. Распределение Максвелла.
1. Кинетическая энергия частицы в силовом поле.
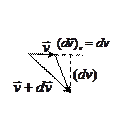

|
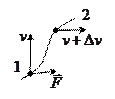 Пусть частица массой
Пусть частица массой  движется пол действием силы
движется пол действием силы 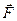 . Элементарная работа этой силы:
. Элементарная работа этой силы: 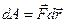 ; (
; ( )
) 
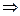
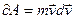 . Скалярное произведение
. Скалярное произведение  ;
;  — проекция вектора приращения скорости
— проекция вектора приращения скорости 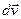 на направление вектора
на направление вектора 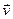 . Она равна
. Она равна 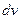 — приращению модуля вектора скорости, тогда
— приращению модуля вектора скорости, тогда 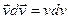 и работа
и работа  . Отсюда видно, что работа результирующей силы
. Отсюда видно, что работа результирующей силы 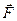 идет на приращение некоторой физической величины
идет на приращение некоторой физической величины  , которую называют кинетической энергией и которая является мерой энергии движения материальной точки.
, которую называют кинетической энергией и которая является мерой энергии движения материальной точки.
 , т.о.
, т.о. 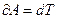 (*)
(*)
При конечном перемещении из т.1 в т.2
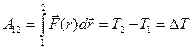 ;
; 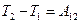 (**)
(**)
3. 10 Распределение Максвелла
Полученная ранее барометрическая формула обязана своим видом тому, что скорости молекул не одинаковы, а распределены определенным образом. Характер этого распределения и определяет вид зависимости плотности молекул от высоты.
n= n0е(-mg/kT)x
Пользуясь этой формулой можно найти вид функции распределения молекул по скорости.
Возьмем сосуд с газом в пустом пространстве в поле сил тяжести. Газ находится в состоянии равновесия и его молекулы каким-то образом распределены по скорости. Сила тяжести действует на Z компоненту скорости (по вертикали), поэтому найдем распределение молекул по значению составляющей скорости vz. Движение вверх вдоль оси Z сопровождается уменьшением Z компоненты скорости. Если на начальной высоте Z0 скорость равна vz0, то на высоте Z значение vzможно найти из закона сохранения энергии:
m(vz0)2/2= m(vz0)2/2+mgZ (*)
Молекулы с энергией m(vz0)2/2≤mgZ не могут подняться выше Z=(vz0)2/2g, они после подъема до Z падают вниз c ускорением.
 Выделим на высоте Z слой dZ с площадью S=1м2. Газ в слое состоит из движущихся вверх и вниз молекул (нас интересуют молекулы вдоль оси Z). Разница между молекулами снизу и сверху состоит в том, что молекулы, приходящие снизу, имеют Z-компоненту скорости с v≥√2gZ, в то время, как молекулы, приходящие сверху, могут иметь Z-компоненту с любыми скоростями от 0 до ∞.
Выделим на высоте Z слой dZ с площадью S=1м2. Газ в слое состоит из движущихся вверх и вниз молекул (нас интересуют молекулы вдоль оси Z). Разница между молекулами снизу и сверху состоит в том, что молекулы, приходящие снизу, имеют Z-компоненту скорости с v≥√2gZ, в то время, как молекулы, приходящие сверху, могут иметь Z-компоненту с любыми скоростями от 0 до ∞.
В условиях равновесия число молекул в слое должно быть постоянно, число молекул, проходящих сверху вниз, должно быть равно числу молекул, проходящих снизу вверх. На высоте Z0 число молекул в единице объема с Z компонентой скорости, лежащей в интервале от vz0 до vz0+dvz0 определяется выражением: dnz0= nz0f(vz0)dvz0
|
|

 N↑=∫nz0vz0f(vz0)dvz0= nz0∫vz0f(vz0)dvz0
N↑=∫nz0vz0f(vz0)dvz0= nz0∫vz0f(vz0)dvz0
|
|
|
|
 Получим: ∫f(vz0)vz0dvz0= е(-mg/kT)z∫ f(vz)vzdvz
Получим: ∫f(vz0)vz0dvz0= е(-mg/kT)z∫ f(vz)vzdvz
|
|
∫f(vz0)vzdvz=e-∫f(vz)vzdvz
 заменили предел интегрирования т. к. vZизм. от 0 до µ
заменили предел интегрирования т. к. vZизм. от 0 до µ
то есть f(vz)=f(vz0)е(-mg/kT)z (**)
Сравнивая это с законом сохранения энергии (*) можно убедится, что функции f(v) должны иметь вид:
f(vz)=Ае и f(vz0)=Ae
Значит f(vz)=Ае
Число молекул в единице объема, с Z компонентой скорости, лежащей в интервале от vZдо vZ+ dvZвыражается формулой
dn=nAe dvZ; a dn/n=Ae dvz –
|
|
Постоянная А находится из усл. нормировки ∫ dn/n=A∫ e-dvz=1
|



| |
|
 Вводится переменная х2 = m(vz)2/2kT =>vZ= √2kT/mx =>dvz= √ dx
Вводится переменная х2 = m(vz)2/2kT =>vZ= √2kT/mx =>dvz= √ dx
Интеграл сводится к ∫ e-хdx = √ π и тогда A = √m/2πkT
И формула распределения принимает вид: f(vz) = dn/ndvZ= (m/2πkT)1/2×e
f(vZ)→0 при vZ→∞
Видно,что доля молекул с Z-компонентой скорости равной 0 не равна 0, она равна А и с повышением Т уменьшается.
Мы получили распределение молекул по Z- составляющей скорости в поле сил тяжести, но это не означает, что распределение связано с действием силы тяжести. И что mg создает это распределение. Сама барометрическая формула является следствием распределения молекул по скорости. Сила тяжести лишь «проявила» существование в газе распределения, поэтому в f(v) сила тяжести не входит (нет g).
Очевидно, что совершенно такие же распределения должны быть и по другим компонентам скорости:
dn/ndvx = Ae
dn/ndvy = Ae
Теперь нужно найти вероятность того, что скорости молекул удовлетворяют трем условиям:
vx лежит в пределах от vx до vx+dvx, vy лежит в пределах от vy до vy+dvy, а vz лежит в пределах от vz до vz+dvz. Значения составляющих скоростей молекул по каждой из осей координат не зависят от значений по другим осям. Поэтому, вероятность того, что скорость молекулы одновременно удовлетворяет трем условиям является «вероятностью сложного события», т.е. равна произведению вероятностей.
Если обозначить число молекул в единице объема газа dnxyz с составляющими по осям dnx, dny, dnz ,то
dnxyz/n = A3e dvxdvydvz v2 = Σ(vi)2
Эта формула показывает, сколько молекул из числа находящихся в единице объема обладают скоростями, составляющие которых по осям координат лежат в интервале между vx и vx+dvx, vy и vy+dvy, vz и vz+dvz , т.е. обладают скоростью, лежащей в интервале заданном и по величине и по направлению. В распределении необходимо учесть все любые направления движения.
Если собрать все молекулы единицы объема газа со скоростями в интервале от vдо v+dv по всем любым направлениям и выпустить их, то они, разлетаясь по всем направлениям, через 1 с окажутся равномерно распределенными в шаровом слое радиусом vи толщиной dv. Число молекул в единице объема этого слоя (объем скоростей) такое же, как и в параллелепипеде объемом dvxdvydvz. Число же молекул во всем слое – это и есть число молекул в единице объема газа, независимо от направления, скорости которых лежат в интервале от v до v+dv:
dn = n(m/2πkT)3/2edΩ; dΩ = 4πv2dv, отсюда:
 dn/n =( 4/√π )(m/2kT) 3/2 v2
dn/n =( 4/√π )(m/2kT) 3/2 v2 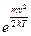 dv
dv
Это и есть закон Максвелла распределения молекул по скоростям.
dn/n – вероятность того, что у произвольно выбранной молекулы газа скорость окажется лежащей в интервале от v до v+dv, Другими словами, это доля всех молекул ед. объема, скорости кот. лежат в интервале от v до v+ dv. Величина
f(v) = dn/ndv = (4/√ π )(m/2kT) 3/2 v2 edv –функция распределения молекул по скоростям.
π )(m/2kT) 3/2 v2 edv –функция распределения молекул по скоростям.
Она определяет долю молекул в единице объема, скорости которых заключены в единичном интервале скоростей вблизи v, включающем данную скорость.
f(v) обращается в 0 при v = 0 и v = ∞, т.е., нет неподвижных молекул и нет молекул с бесконечно большой скоростью. Имеется максимум при vн, т.е. наибольшая часть молекул движется со скоростью v ≈ vн, т.е. вероятность того, что молекула имеет скорость vн – наибольшая, поэтому vн называют наиболее вероятной скоростью.
Пользуясь кривой распределения молекул по скоростям можно графически найти долю молекул dn/n в единице объема газа, скорости которых лежат в заданном интервале скоростей dv. Графически - это площадь с основанием dv и высотой f(v). Вся площадь под кривой f(v) соответствует общему числу молекул в единице объема.
Вид кривой зависит от природы газа и от Т. С повышением Т максимум смещается в сторону больших скоростей, но площадь под кривой остается постоянной, т.к. n = const.
При выводе распред. Максвелла по скоростям совершенно не принимали во внимание столкновения молекул между собой, хотя они изменяют скорость и влияют на распределение. В действительности именно благодаря столкновениям и устанавливается максвелловское распределение по скоростям. При каждом столкновении скорость одной молекулы увеличивается, другой уменьшается. Максвелл предположил, что равновесному состоянию отвечает такое, при котором число молекул, скорости которых увеличиваются при столкновении равно числу молекул, скорости которых уменьшаются при столкновениях. Такому состоянию и соответствует распределение Максвелла.
Позже Больцман показал, что если газ находится в состоянии с немаксвелловским распределением, то благодаря столкновениям он сам собой переходит в состояние с максвелловским распределением.
Распределение Максвелла (иногда говорят Максвелла -Больцмана) – это равновесное распределение. Теперь можно дать определение хаотичному движению: движение молекул полностью хаотично, если скорости распределены по закону Максвелла.
Б-20
1. Полная механическая энергия частицы.
2.Равенство поперечных размеров тел и лоренцево сокращение.
3. Средние скорости молекул: арифметическая, квадратичная, наиболее вероятная.
1. Полная механическая энергия частицы.
Т.о. приращение кинетической энергии частицы равно элементарной работе 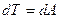 всех сил, действующих на частицу. Если частица находится в стационарном поле консервативных сил, то на нее действует консервативная сила
всех сил, действующих на частицу. Если частица находится в стационарном поле консервативных сил, то на нее действует консервативная сила 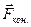 со стороны поля. кроме этого на неё могут действовать и другие силы
со стороны поля. кроме этого на неё могут действовать и другие силы 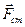 ; т.е. результирующая сила
; т.е. результирующая сила  .
.
Работа всех этих сил идет на изменение приращения кинетической энергии частицы
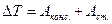
Известно также, что работа консервативных сил поля равна убыли потенциальной энергии частицы.
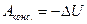 , значит
, значит 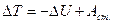 или
или 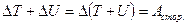
Т.о. работа сторонних сил идёт на приращение величины 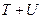 . Эту величину называют полной механической энергией частицы в поле
. Эту величину называют полной механической энергией частицы в поле 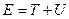 . Отсюда видно, что
. Отсюда видно, что 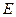 определяется с точностью до постоянной, так как с точность до
определяется с точностью до постоянной, так как с точность до 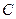 определяется
определяется  . Теперь можно записать
. Теперь можно записать
 (***)
(***)
т.е. приращение полной механической энергии частицы на некотором пути равно работе сторонних сил, действующих на частицу на этом пути; Если 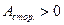 , то полная механическая энергия частицы растёт при
, то полная механическая энергия частицы растёт при 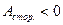 , — уменьшается.
, — уменьшается.
Пример: Тело, падающее с обрыва
 .
.
Средние скорости молекул
1. Средняя арифметическая скорость<v> по определению равна отношению суммы скоростей всех молекул единицы объема к числу молекул единицы… Число молекул в единице объема dnv, скорости которых заключены в интервале от… ∞ <v> = ∫vf(v)dv , подставив f(v), получим:Б21
1. Закон сохранения механической энергии частицы.
2. Преобразования Лоренца.
4. Обратимые и необратимые термодинамические процессы.
1. Закон сохранения механической энергии частицы.
Из выражения 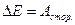 следует, что в стационарном поле консервативных сил полная механическая энергия частицы может изменяться под действием только сторонних сил, отсюда вытекает закон сохранения механической энергии частицы.
следует, что в стационарном поле консервативных сил полная механическая энергия частицы может изменяться под действием только сторонних сил, отсюда вытекает закон сохранения механической энергии частицы.
Если сторонние силы отсутствуют, то полная механическая энергия частицы в стационарном поле консервативных сил остается постоянной.
 ;
; 
Закон сохранения позволяет решать многие вопросы, не привлекая уравнения движения, которые часто приводят к ??? расчетам.
3. 1 Обратимые и необратимые процессы
Для расширения представлений о термодинамических процессах уточним понятие обратимого процесса: процесс, совершаемый системой наз. обратимым, если после него можно возвратить систему и все тела, взаимодействующие с ней, в их начальное состояние таким образом, чтобы в других телах не возникало каких-либо остаточных изменений.
Необходимое условие обратимости терм. процесса – его равновесность, т.е. всякий обратимый процесс всегда является равновесным (квазистат). Однако не всякий равновесный процесс является обратимым. Например, квазистататический процесс равномерного движения по поверхности под действием силы тяжести и трения – процесс необратимый.
Пример обратимого процесса – незатухающие колебания тела, подвешенного на пружине в вакууме. Система тело-пружина консервативна. Ее механические колебания не вызывают никаких изменений в энергии теплового движения частиц системы. Изменение состояния системы связано с изменением ее конфигурации и скорости движения тела, которые полностью повторяются через период.
Пример необратимого процесса – торможение тела под действием силы трения. Если сила трения единственная сила, то скорость тела уменьшается и оно останавливается. При этом энергия мех движ. тела, как целого уменьш. и расходуется на увел. энергии тепл. движ. частиц тела и среды. Другими словами, за счет нач. кинет. эн. тела (Wк) растет внутрення энергия U тела и среды, нагревающихся при трении ΔU = Wк. Этот прямой процесс протекает самопроизвольно, он идет без каких либо процессов, происходящих с окружающими телами. Но для осуществления обратного процесса возвращения системы в исходное состояние необходимо, чтобы остановившееся тело вновь пришло в движение за счет энергии, выделившейся при его охлаждении и окружающей среды. Известно, что хаотическое движение тела, т.е., U не может самопроизвольно привести к упорядоченному движению всех частиц тела, как целого. Для реализации этого необходим дополнительный, так называемый компенсирующий процесс. Он заключается в охлаждении тела и окружающей среды до первоначальной Т, т.е., в отдаче ими некоторому другому телу теплоты Q = Wк и в совершении над рассматриваемым телом работы, равной Wк. Поэтому, хотя в результате прямого и обратного процесса система тело-среда возвратилась в исходное состояние, состояние внешних тел изменяется (меняется Т, затем совершается работа, т.е. меняются координаты). Следовательно, процессы сопровождающиеся трением необратимы.
Процесс теплообмена между двумя телами с разной Т приводит к выравниванию средних энергий тепл. движения частиц обоих тел. Энергия частиц более нагретого тела уменьшается, менее нагретого – увеличивается. В итоге Т1 = Т2. Процесс идет самопроизвольно, как только обеспечен контакт между телами. Обратный процесс – нагревание одного тела за счет охлаждения другого, имевшего вначале Т1 = Т2, самопроизвольно не протекает. Для него используется холодильное устройство, работа которого приводит к изменению состояния других внешних тел. Значит процесс теплообмен при конечной ΔТ является необратимым. Можно показать, что необратимыми являются процессы диффузии и растворения.
Из всех этих примеров необратимых процессов можно сделать общие выводы: Все они в прямом направлении происходят самопроизвольно, а для осуществл. обр. проц. требуется одновременное протекание компенсирующих процессов. Все реальные процессы идут с конечной скоростью и сопровождаются трением и теплообменом при конечной разности температур тел, находящихся в тепловом контакте, значит все реальные процессы, строго говоря, необратимы. Однако в некоторых случаях условия протекания процесса таковы, что их приближенно можно считать обратимыми.
Б-22
1. Кинематика вращательного движения: угол поворота, угловая скорость, угловое ускорение, связь между линейной и угловой скоростью.
2. Релятивистский импульс. Основное уравнение релятивистской механики.
3. Энтропия. Энтропия идеального газа.
1. Кинематика и динамика вращательного движения.
 Поворот тела на некоторый угол
Поворот тела на некоторый угол 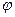 можно задать в виде отрезка длина которого
можно задать в виде отрезка длина которого 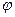 , а направление совпадает с осью вращения и определяется правилом правого винта: Направление должно быть таким, чтобы глядя вдоль него, мы видели поворот совершающийся по часовой стрелке.
, а направление совпадает с осью вращения и определяется правилом правого винта: Направление должно быть таким, чтобы глядя вдоль него, мы видели поворот совершающийся по часовой стрелке.
 При поворотах на очень малые углы, путь проходимый точкой можно считать прямолинейным, поэтому два последовательных малых поворота
При поворотах на очень малые углы, путь проходимый точкой можно считать прямолинейным, поэтому два последовательных малых поворота  и
и  (вокруг разных осей, оси
(вокруг разных осей, оси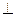 в данном случае) обуславливают как видно из рис., такое же перемещение,
в данном случае) обуславливают как видно из рис., такое же перемещение,  любой точки тела, как и поворот
любой точки тела, как и поворот 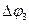 получаемый из
получаемый из  и
и  сложением о правилу параллелограмма. Значит очень малые повороты можно рассматривать как векторы. Направление вектора поворота
сложением о правилу параллелограмма. Значит очень малые повороты можно рассматривать как векторы. Направление вектора поворота  , связывается с направлением вращения тела, следовательно
, связывается с направлением вращения тела, следовательно  не является истинным вектором, а является псевдовектором.
не является истинным вектором, а является псевдовектором.
|
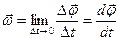 называется угловой скоростью тела направлена вдоль оси вращения, в сторону, определяемую правилом правого винта — тоже псевдовектор, модуль
называется угловой скоростью тела направлена вдоль оси вращения, в сторону, определяемую правилом правого винта — тоже псевдовектор, модуль 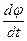 , если
, если 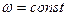 — равномерное вращение
— равномерное вращение 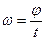 , для равномерного движения
, для равномерного движения 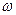 -угол поворота в единицу времени.
-угол поворота в единицу времени. 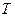 период вращения
период вращения 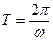 число оборотов
число оборотов 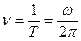 , а
, а  .
.
 Понятия
Понятия 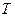 и
и  можно сохранить и для неравномерного вращения, понимая под ними мгновенное вращение.
можно сохранить и для неравномерного вращения, понимая под ними мгновенное вращение.
Вектор 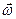 может изменяться как за счет изменения скорости вращения оси (по величине), так и за счет поворота оси вращения в пространстве ( по направлению). Если за
может изменяться как за счет изменения скорости вращения оси (по величине), так и за счет поворота оси вращения в пространстве ( по направлению). Если за 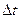
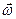 получает приращение
получает приращение 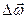 то изменение угловой скорости со временем характеризуется угловым ускорением
то изменение угловой скорости со временем характеризуется угловым ускорением
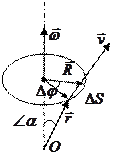
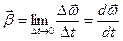 — тоже псевдовектор.
— тоже псевдовектор.
Точки вращающегося тела имеют разные линейные скорости, которые определяют 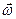 и
и  . Если за
. Если за 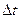 тело повернулось на
тело повернулось на  , то
, то 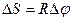 . Линейная скорость точки
. Линейная скорость точки 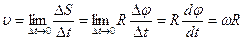 ; т.е.
; т.е. 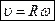 .
.
Найдем связь между векторами  и
и 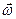 . Положение для модулей точки определяет
. Положение для модулей точки определяет 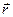 . Из рис. видно, что
. Из рис. видно, что 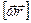 совпадает с
совпадает с  по направлению, модуль
по направлению, модуль 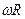 равен
равен 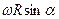 .
.
Модуль нормального ускорения точек 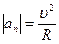 или через
или через 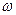
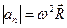 .
.
Когда ось вращения не поворачивается в пространстве, тогда тангенциальное ускорение:
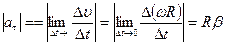 ;
; 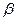 -модуль угловой скорости, т.е
-модуль угловой скорости, т.е 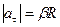 .
.
Т.о. нормальное и тангенциальное ускорение растут пропорционально  .
.
3. Энтропия (от греческого слова преобразовать, превращать)
В середине ХІХ века было сделано существенное открытие, касающееся обратимых т. процессов. Это открытие связано с именами Карно и Клаузиуса и является существенной частью 2-го закона термодинамики.
Оказалось, что наряду с внутренней энергией у тела имеется еще одна важная функция состояния – энтропия. Так же, как и внутренняя энергия, энтропия определяется с точностью до произвольной постоянной. В опытах проявляется значение разности энтропий.
Если тело или система при бесконечно малом переходе из одного состояния в другое при температуре Т получает малое количество теплоты δQ, то отношение δQ/Т является полным дифференциалом некоторой функции S. Эта функция и есть энтропия, определяющаяся, таким образом равенством:
dS = δQ/Т, при малом переходе,
а для конечного изменения: ΔS = S2-S1 = 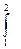 δQ/Т
δQ/Т
Сущность энтропии заключается в следующем: Переход системы из одного состояния в другое может произойти бесчисленным количеством способов (разные кривые на графике с окончанием в одних
| |
 будет иметь одинаковое значение, т.е., не зависит от вида перехода, а определяется только состояниями системы в точках 1 и 2. Значит S является функцией состояния.
будет иметь одинаковое значение, т.е., не зависит от вида перехода, а определяется только состояниями системы в точках 1 и 2. Значит S является функцией состояния.
Например, тело нагревают равномерно от 20 до 25˚С, при этом оно получает по 5 Дж теплоты на 1 К. Тогда прирост энтропии, примерно, равен S2-S1 ≈ 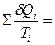 5/293,5+5/294,5+5/295,5+5/296,5+5/297,5 Дж/К.
5/293,5+5/294,5+5/295,5+5/296,5+5/297,5 Дж/К.
Наиболее просто выразить изменение энтропии при изотермическом процессе: S2-S1 =  =Q/Т, т.к., Т = const. Пример: при таянии 1 кг льда
=Q/Т, т.к., Т = const. Пример: при таянии 1 кг льда
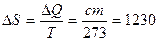 Дж/К.
Дж/К.
За нуль энтропии может быть принято значение энтропии любого состояния, (кипящей воды, плавящегося льда). Однако, в некоторых случаях за нуль
| |
S = 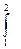 νСрdT/T если нагрев происходил при р= const. Чтобы определение энтропии dS = δQ/Т было обоснованным, необходимо доказать, что в любом обратимом круговом процессе интеграл от δQ/Т тождественно равен 0.
νСрdT/T если нагрев происходил при р= const. Чтобы определение энтропии dS = δQ/Т было обоснованным, необходимо доказать, что в любом обратимом круговом процессе интеграл от δQ/Т тождественно равен 0.
 δQ/Т ≡0, т.е. S = const
δQ/Т ≡0, т.е. S = const
Если известно уравнение состояния вещества, то энтропия (с точностью до const) может быть вычислена весьма просто. По определению:
dS = δQ/Т , подставив сюда δQ из 1-го з-на т. получим:
dS = (m/M)(CvdT/T+RdV/V)
Взяв определенный интеграл, получим
S2-S1 = (m/M)(CvlnT2 /T1+ RlnV2/V1).
Это выражение для энтропии идеальных газов: она возрастает с повышением Т и при увеличении объема газа при подводе к нему теплоты δQ.
Б-23
1. Нормальное ускорение и модуль тангенциального ускорения при вращении.
2. Кинетическая энергия релятивистской частицы.
3. Принцип возрастания энтропии. Примеры: при теплообмене, при расширении в вакуум, при механическом движении в сосуде с газом.
1. Вектор 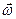 может изменяться как за счет изменения скорости вращения оси (по величине), так и за счет поворота оси вращения в пространстве ( по направлению). Если за
может изменяться как за счет изменения скорости вращения оси (по величине), так и за счет поворота оси вращения в пространстве ( по направлению). Если за 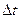
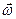 получает приращение
получает приращение 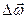 то изменение угловой скорости со временем характеризуется угловым ускорением
то изменение угловой скорости со временем характеризуется угловым ускорением
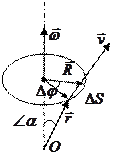
 — тоже псевдовектор.
— тоже псевдовектор.
Точки вращающегося тела имеют разные линейные скорости, которые определяют 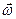 и
и  . Если за
. Если за 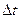 тело повернулось на
тело повернулось на  , то
, то 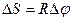 . Линейная скорость точки
. Линейная скорость точки  ; т.е.
; т.е. 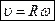 .
.
Найдем связь между векторами  и
и 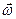 . Положение для модулей точки определяет
. Положение для модулей точки определяет 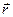 . Из рис. видно, что
. Из рис. видно, что 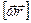 совпадает с
совпадает с  по направлению, модуль
по направлению, модуль 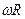 равен
равен 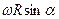 .
.
Модуль нормального ускорения точек 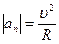 или через
или через 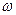
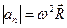 .
.
Когда ось вращения не поворачивается в пространстве, тогда тангенциальное ускорение:
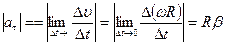 ;
; 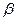 -модуль угловой скорости, т.е
-модуль угловой скорости, т.е 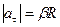 .
.
Т.о. нормальное и тангенциальное ускорение растут пропорционально  .
.
3. Принцип возрастания энтропии
Необратимость всех реальных процессов в конечном счете связана с тем, что в каждом из них присутствует один из самопроизвольных процессов. В реальных явлениях невозможно избежать ни самопроизвольного расширения, ни трения, ни теплового рассеяния. Во всем этом есть один общий признак. Он состоит в том, что во всех самопроизвольных процессах энтропия возрастает.
Примеры:
а) При теплообмене между двумя телами с разными температурами общее изменение энтропии равно:
S2-S1 = Q1/Т1+ Q2/Т2, где Q1 – тепло полученное, холодным телом; Q2 – тепло, отданное горячим телом.
т.к. Т2> Т1 то Q1 = - Q2>0 - тепло, отданное телом, считается <0, тогда S2-S1 = Q1(1/ Т1-1/ Т2)>0, т.е., при теплообмене общая энтропия системы возрастает.
б) Если внутри сосуда с газом происходит интенсивное механическое движение (вертится колесо), то температура газа за счет внутреннего трения растет (при этом V = const), поэтому энтропия системы изменится: S2-S1 = (m/M)(CvlnT2/T1), т.е., снова возрастает.
в) При расширении газа в пустоту при Т = const приращение энтропии: S2-S1 = (m/M)(RlnV2/V1); опять >0.
Итак, во всех самопроизвольных процессах энтропия системы возрастает. Это имеет важное значение для необратимых процессов.
Для обратимых процессов прирост энтропии был бы равен dS = δQ/T; Т.к. каждый необратимый процесс сопровождается самопроизвольными явлениями, идущими с повышением энтропии, то приращение энтропии при сообщении δQ для них будет выше, чем приращение, которое имело бы место при обратимом процессе, т.е. dS ≥ δQ/T.
Если система теплоизолирована (адиабатный процесс), то δQ = 0 и это утверждение имеет вид:
dS = 0, S = const для обратимых процессов и
dS> 0 (для необратимых);
т.е., в теплоизолированных системах возможны только процессы с возрастанием энтропии, или с ее сохранением.
Если в предыдущие формулы ввести вместо знака равенства знак ≥, то закон возрастания энтропии запишется как для обратимых, так и для необратимых процессов:
dS ≥ δQ/T (для обратимых знак =, для необратимых знак >).
Эта ф-ла передает содержание 2-го закона т.
Можно объединить 1 и 2 з-ны т. и записать их в виде: dS ≥ (dU+pdV)/T
Принцип возрастания энтропии относится к закрытым системам. Если же система общается с внешней средой, т.е. она открыта, то энтропия может и убывать.
Б-24
1. Момент импульса частицы. Момент силы. Уравнение моментов.
2. Связь между массой и энергией в релятивистской механике.
3. Энтропия в необратимых процессах. Энтропия в изолированной системе (адиабатический процесс)
1. момент импульса частицы. Момент силы.
Кроме энергии и импульса существует ещё Одина физическая величина. С которой связан закон сохранения — это момент импульса. Моментом импульса частицы 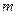 относительно точки О называется вектор
относительно точки О называется вектор  равный
равный 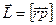 ,
, 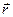 -радиус; -импульс.
-радиус; -импульс.
Т.е.  является ??? вектором. Его направление выбрано так, что вращение вокруг О в направлении
является ??? вектором. Его направление выбрано так, что вращение вокруг О в направлении 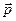 и вектор
и вектор  образует правовинтовую систему. Модуль
образует правовинтовую систему. Модуль 
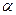 угол между
угол между  и
и 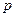
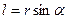 плечо вектора
плечо вектора 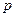 относительно О.
относительно О.
Найдем с какой величиной связано изменение вектора  во времени:
во времени:

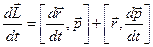 .
.
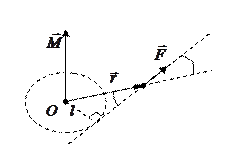 Т.к т.о неподвижна, то
Т.к т.о неподвижна, то 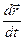 равно скорости частицы, т.е. совпадает с
равно скорости частицы, т.е. совпадает с 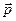 , т.е.
, т.е.  . Далее
. Далее 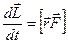 — второй закон Ньютона и
— второй закон Ньютона и 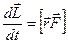 ; Величина
; Величина 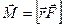 —момент силы аксиальный вектор.
—момент силы аксиальный вектор. 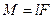 ,
, 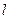 —плечо силы
—плечо силы 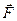 относительно т.О.
относительно т.О.
Т.о производная по 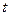 момента импульса
момента импульса 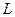 частицы, относительно некоторой т.О выбранной системы отсчета равна моменту равнодействующей силы
частицы, относительно некоторой т.О выбранной системы отсчета равна моменту равнодействующей силы 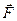 относительно этой точки
относительно этой точки 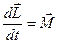 . Это уравнение называют уравнением моментов.
. Это уравнение называют уравнением моментов.
Если система отсчета является неинерциальной, то в момент силы 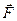 включает в себя как момент сил взаимодействия, так и момент сил инерции (относительно той же т.О). Из уравнения моментов следует что если
включает в себя как момент сил взаимодействия, так и момент сил инерции (относительно той же т.О). Из уравнения моментов следует что если 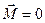 , то
, то  —равномерное вращательное движение. Т.е. если момент всех сил относительно т.О системы отсчета равен О, в течение интересующего нас
—равномерное вращательное движение. Т.е. если момент всех сил относительно т.О системы отсчета равен О, в течение интересующего нас 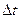 , то момент импульса частицы относительно этой точки остается постоянным.
, то момент импульса частицы относительно этой точки остается постоянным.
Уравнение моментов позволяет найти 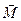 точки относительно О в любой момент времени если известна
точки относительно О в любой момент времени если известна  частицы относительно точки. Для этого достаточно продифференцировать уравнение
частицы относительно точки. Для этого достаточно продифференцировать уравнение  . Кроме этого, если известна зависимость
. Кроме этого, если известна зависимость 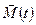 , то можно найти приращение момента импульса частицы относительно т.О за любой промежуток времени. Для этого необходимо проинтегрировать уравнение
, то можно найти приращение момента импульса частицы относительно т.О за любой промежуток времени. Для этого необходимо проинтегрировать уравнение 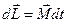 , тогда
, тогда
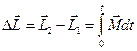
Выражение 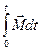 —импульс момента силы подобно
—импульс момента силы подобно  , т.е. приращение момента импульса частицы за любой промежуток времени равно импульсу момента силы за э
, т.е. приращение момента импульса частицы за любой промежуток времени равно импульсу момента силы за э
то время.
3. Для обратимых процессов прирост энтропии был бы равен dS = δQ/T; Т.к. каждый необратимый процесс сопровождается самопроизвольными явлениями, идущими с повышением энтропии, то приращение энтропии при сообщении δQ для них будет выше, чем приращение, которое имело бы место при обратимом процессе, т.е. dS ≥ δQ/T.
Если система теплоизолирована (адиабатный процесс), то δQ = 0 и это утверждение имеет вид:
dS = 0, S = const для обратимых процессов и
dS> 0 (для необратимых);
т.е., в теплоизолированных системах возможны только процессы с возрастанием энтропии, или с ее сохранением.
Если в предыдущие формулы ввести вместо знака равенства знак ≥, то закон возрастания энтропии запишется как для обратимых, так и для необратимых процессов:
dS ≥ δQ/T (для обратимых знак =, для необратимых знак >).
Эта ф-ла передает содержание 2-го закона т.
Можно объединить 1 и 2 з-ны т. и записать их в виде: dS ≥ (dU+pdV)/T
Принцип возрастания энтропии относится к закрытым системам. Если же система общается с внешней средой, т.е. она открыта, то энтропия может и убывать.
Б-25
1. Закон сохранения момента импульса.
2. Центробежная сила инерции.
3. Второй закон термодинамики.
1. Закон сохранения момента импульса системы.
Рассмотрим систему состоящую из 2 частиц, на которые действуют также силы  и
и  . Момент импульса является аддитивной величиной. Для системы равен векторной сумме моментов импульса отдельных частиц относительно одной и той же точки
. Момент импульса является аддитивной величиной. Для системы равен векторной сумме моментов импульса отдельных частиц относительно одной и той же точки 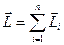 .
.
Нам известно, что  —моменту всех сил, действующих на частицу, а изменение момента системы
—моменту всех сил, действующих на частицу, а изменение момента системы  , тогда
, тогда  ;
;  ;
;
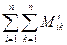 — суммарный момент всех внутренних сил действующих на частицы.
— суммарный момент всех внутренних сил действующих на частицы.
 — суммарный момент всех внешних сил действующих на частицы.
— суммарный момент всех внешних сил действующих на частицы.
Значит для двух частиц:
 .
.
Суммарный момент внутренних сил относительно любой точки равен 0. силы взаимодействия между частицами 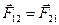 по 3му закону Ньютона действуют по одной прямой, значит имеют одинаковое плечо, поэтому момент каждой пары внутренних сил равен 0.
по 3му закону Ньютона действуют по одной прямой, значит имеют одинаковое плечо, поэтому момент каждой пары внутренних сил равен 0.
Т.о.  ; т.е. системы изменяются под действием внешних сил
; т.е. системы изменяются под действием внешних сил 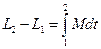 . Если внешние силы отсутствуют
. Если внешние силы отсутствуют 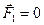 ,
, 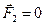 , то
, то 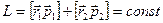 , является аддитивным сохраняющейся величиной. Т.е. момент импульса замкнутой системы частиц остается постоянным, не меняется со временем. Это справедливо относительно любой точки инерциальной системы отсчета:
, является аддитивным сохраняющейся величиной. Т.е. момент импульса замкнутой системы частиц остается постоянным, не меняется со временем. Это справедливо относительно любой точки инерциальной системы отсчета:  т.е. моменты импульса отдельных частей
т.е. моменты импульса отдельных частей  одной части системы происходят за счет убыли
одной части системы происходят за счет убыли 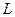 другой части (относительно одной точки).
другой части (относительно одной точки).
Закон справедлив и в неинерциальной системе отсчета в тех случаях когда суммарный момент всех внешних сил, включая силы инерции равен нулю.
 Закон играет такую же роль как закон сохранения энергии импульса. Он позволяет решать разные задачи, не рассматривая детально внутренние процессы. Пример: разгоняют????
Закон играет такую же роль как закон сохранения энергии импульса. Он позволяет решать разные задачи, не рассматривая детально внутренние процессы. Пример: разгоняют????
Момент импульса 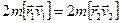 ;
;  т.е.
т.е.  уменьшается как
уменьшается как 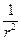 . Этот эффект широко используют гимнасты, фигуристы и т.д. здесь мы интересуемся силами взаимодействия и т.д. у незамкнутых систем может сохраняться не сам
. Этот эффект широко используют гимнасты, фигуристы и т.д. здесь мы интересуемся силами взаимодействия и т.д. у незамкнутых систем может сохраняться не сам 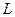 , а его проекция на некоторую неподвижную ось
, а его проекция на некоторую неподвижную ось 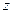 . Это бывает, когда
. Это бывает, когда 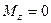 всех внешних сил.
всех внешних сил.
 ;
; 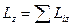 ;
; 
В физике понятие момента импульса расширяют на немеханические системы (с электромагнитным излучением, в атомах, ядра и др.) где не действуют законы Ньютона. Здесь закон сохранения момента импульса уже не является следствием законов Ньютона, а представляет собой самостоятельный принцип, является обобщением опытных фактов и является одним из фундаментальных законов наряду с законами сохранения энергии и импульса.
3. Второй закон термодинамики
Второй з-н термодинамики состоит в утверждении, что энтропия в теплоизолированной системе возрастает. Существуют и другие формулировки 2-го з-на т. Исторически он вошел в науку в виде постулата Томсона о невозможности создании вечного двигателя второго рода.
Вечным двигателем 1-го рода называют машину, которая создает работу из ничего, вопреки 1 з-ну термодинамики (з-ну сохранения энергии). Вечным двигателем 2-го рода называют такой двигатель, который производит работу при помощи периодически действующей машины за счет одного только отнятия теплоты от окружающей среды, т.е. с η =1. Двигатель 2-го рода это тепловая машина, работающая с нагревателем, но без холодильника. Она могла бы проработать один такт, газ в сосуде с поршнем расширился бы, но на этом работа двигателя закончилась, т.к., для продолжения работы машины часть тепла, полученного газом, необходимо передать холодильнику. Формально, невозможность двигателя 2-го рода видна из ф-лы максимального кпд. При отсутствии теплового перепада Т2 = Т1, η = 0; η = (Т1-Т2)/Т1 = 1- Т2/Т1.
Невозможно осуществить периодически действующий вечный двигатель, комбинируя изотермическое расширение с процессом адиабатного сжатия. Такой процесс невозможен, даже, если бы его удалось сделать обратимым. При изотермическом расширении тела энтропия S падает. Значит процесс сжатия должен приводить к возрастанию S. Этого однако не может сделать адиабатный процесс (при нем S = const).
Принятой формулировке 2-го з-на т. вполне соответств. также постулат Клаузиуса, который состоит в утверждении о невозможности перехода тепла от менее нагретого тела к более нагретому без компенсации, т. е. без совершения работы внешними силами.
Б-26
1. Вращение тела вокруг неподвижной оси. Момент инерции твердого тела.
2. Теорема Штейнера.
3. Статистический смысл второго закона термодинамики.
1. Кинетическая энергия вращающегося тела.
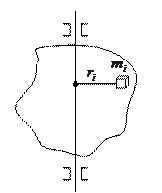 Рассмотрим абсолютно твердое тело, вращающееся вокруг неподвижной оси, проходящей через него. Разобьем его на частицы с малыми объемами и массами
Рассмотрим абсолютно твердое тело, вращающееся вокруг неподвижной оси, проходящей через него. Разобьем его на частицы с малыми объемами и массами 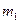 ,
,  …. находящиеся на расстояние
…. находящиеся на расстояние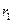 ,
, 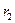 … от оси вращения. Разным
… от оси вращения. Разным  будут соответствовать, разные
будут соответствовать, разные  ,
,  … кинетическая энергия вращения всего тела сложится из энергий составляющих его частицу
… кинетическая энергия вращения всего тела сложится из энергий составляющих его частицу
 т.к.
т.к. 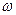 всех частиц одинакова, то
всех частиц одинакова, то 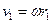 ,
,  … тогда
… тогда
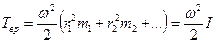 т.е.
т.е. 
Формула справедлива для тела. которое вращается вокруг неподвижной оси. Если тело катится (шар, колесо, и т.д.), то энергия движения складывается из энергии вращения и энергии поступательного движения, т.е. для тела массой 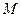 , моментом инерции
, моментом инерции 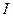 , скоростью поступательного движения
, скоростью поступательного движения 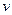 и вращения
и вращения 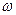
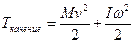 ;
;  ;
;
формула справедлива для произвольного движения, поскольку его можно разложить на совокупность вращения относительно оси инерции и поступательного движения.
3. Статистический смысл II начала термодинамики
Состояние макросистемы может быть охарактеризовано параметрами p, V, T, ν и др. В этом случае говорят, что задано макросостояние. Можно также задать состояние макросистемы более детально, через характеристики всех молекул (их скорости, энергии, координаты), тогда такое детальное описание называют микросостоянием.
Любое макросостояние системы может быть реализовано различными способами, или микросостояниями. Число различных микросостояний, соответствующих данному макросостоянию, называется статистическим весом макросостояния.
В качестве примера рассмотрим способы, которыми могут распределяться N = 4 молекулы с номерами №1, 2, 3, 4 между двумя половинами сосуда с газом без учета распределения Максвелла по скоростям, рис. . Вероятность того, что любая из молекул может находиться в половине А равна, очевидно, 1/2. Вероятность одновременного пребывания одной и другой молекул 1/2·1/2 = 1/22 как вероятность независимых событий, для трех молекул - 1/23 , четырех – 1/24. Вероятность любого размещения 4-х молекул также равна 1/24. Каждое размещение это микросостояние системы и вероятность каждого из них одинакова и равна 1/24. Все возможные распределения 4-х молекул по половинам А и В сосуда приведены в таблице.
А В
 | |||||
| | |||||
 | |||||

 | |||||||
| | |||||||
| | |||||||
 | |||||||
Рис.
| Макросостояния | Способы реализации макросостояний | Число способов, Ω | Обычная вероятность, Р | ||
| А | В | А № мол. | В № мол. | ||
| - | 1,2,3,4 | 1/16 | |||
| 2, 3, 4 1, 3, 4 1, 2, 4 1, 2, 3 | 4/16 | ||||
| 1,2 1,3 1,4 2,3 2,4 3,4 | 3,4 2,4 2,3 1,4 1,3 1,2 | 6/16 | |||
| 1, 2, 3 1, 2, 4 1, 3, 4 2, 3, 4 | 4/16 | ||||
| 1, 2, 3, 4 | - | 1/16 |
Как видно из таблицы, всего микросостояний – 16 = 24 =2N.
Под макросостоянием в данном случае будем понимать состояние, при котором в половине А сосуда: находится, например одна молекула (любая), а в половине В – три любые молекулы. Такие состояния реализуется 4-мя способами. Статистический вес данного макросостояния равен 4, а вероятность 4/16.
Макросостояние с 2-мя молекулами в каждой из половин, реализуется с помощью 6 микросостояний и его статистический вес Ω=6, а вероятность этого макростояния максимальна.
Предположим, что вначале все молекулы находились в половине А сосуда, затем некоторые из молекул, двигаясь беспорядочно, перейдут в В, это означает, что «газ» расширился. Далее макросостояние системы будет меняться случайным образом, но чаще будет реализоваться то из них, которому соответствует максимальное Ω, т.е. более вероятное. Может произойти так, что все четыре молекулы снова случайно окажутся в половине А, т.е. «газ», вначале расширившись, самопроизвольно сожмется. Т.е. процесс расширения оказался обратимым. Это может произойти довольно скоро для 4-х молекул из-за их высоких скоростей и быстрой смены состояний. Однако, вероятность такого события 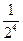 для 4х молекул и равна
для 4х молекул и равна  для N молекул, т.е. быстро уменьшается с ростом числа молекул. Если в сосуде N=100 молекул, то Р » 10-30 .
для N молекул, т.е. быстро уменьшается с ростом числа молекул. Если в сосуде N=100 молекул, то Р » 10-30 .
Такова вероятность того, что газ самопроизвольно сожмется в одной половине сосуда. А вероятность того, что молекулы равномерно распределятся по объему, растет с N. Таким образом, отсюда следует важный вывод: предоставленная самой себе макросистема стремится перейти от менее вероятных состояний к более вероятным. Это является причиной необратимости т. процессов. Обратимый процесс, в принципе, возможен, но его вероятность ничтожно мала.
Таким образом, 2-ой закон термодинамики. указывает на необратимость перехода работы (механической энергии) в тепло, поскольку обратный переход – теплоты в работу означает переход от более вероятного состояния к менее вероятному.
Понятие необратимости процессов применимо только для макросистем, для небольшого числа частиц оно неприменимо. Четыре молекулы возможно соберутся в одной половине сосуда, т.е. «газ» самопроизвольно сожмется. При большом N в состоянии равновесия число молекул в обоих половинах сосуда можно считать одинаковым.
Б-27
1. Преобразования Галилея.
2. Сила Кориолиса.
3. Энтропия и вероятность.
1. Преобразование Галилея
 позволяет определить величины при переходе от одной инерциальной системы к другой.
позволяет определить величины при переходе от одной инерциальной системы к другой. 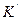 движется со скоростью
движется со скоростью  относительно
относительно  . Взяв начало отсчета времени, момент когда системы совпадали запишем: соотношение между
. Взяв начало отсчета времени, момент когда системы совпадали запишем: соотношение между 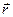 и
и 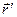 одной и той же точки
одной и той же точки 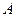 в
в 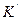 и
и  системе.
системе.
 ;
;  ;
; 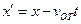 ;
;  ;
; 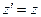 ; (*)
; (*)
Подразумевается, что длины отрезков и ход времени не зависит от состояния движения и одинаковы в системе и 
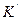 . Предположение об абсолютности пространства и времени лежит в основе Ньютоновской механики подтвержденной многочисленными экспериментами для
. Предположение об абсолютности пространства и времени лежит в основе Ньютоновской механики подтвержденной многочисленными экспериментами для 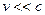 . Продифференцировав, получим
. Продифференцировав, получим
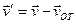 - закон преобразования скоростей.
- закон преобразования скоростей.
После второго дифференцирования 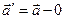
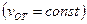 т.е. ускорение не изменяется. Уравнения (*) называются преобразованием Галилея. Итого:
т.е. ускорение не изменяется. Уравнения (*) называются преобразованием Галилея. Итого:
 ;
;
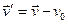 ;
;
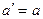 ;
;
Принцип относительности Галилея
Значит ускорение какого-либо тела во всех системах отсчета, движущихся друг относительно друга прямолинейно и равномерно одинаково. Тогда если одна из систем инерциальная, то другая также будет инерциальная 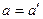 .
.
А значит и силы действующие на тела в разных инерциальных системах одинаковы. Масса в Ньютоновской механике также одинакова во всех системах отсчета. Из сказанного следует вывод, что уравнение динамики 
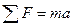 не изменяется при переходе от одной инерциальной системы отсчета к другой или как говорят они инвариантны по отношению к преобразованию координат, соответствующему переходу от одной инерциальной системы отсчета к другой. Это значит что, с механической точки зрения все инерциальные системы отсчета эквивалентны, ни одной из них нельзя отдать предпочтение перед другими. Практически ни какими опытами нельзя установить находится ли данная ИСО в покое или движется равномерно и прямолинейно. Находясь, например, в вагоне поезда, движущегося равномерно и прямолинейно нельзя установить (не выглянув в окно) движется ли он или находится в состоянии покоя. Мяч в вагоне поезда получит такое же ускорение, как и на Земле при действии одинаковой силы. Свободное падение тел и другие механические процессы будут происходить в вагоне также как если бы он покоился. подобное наблюдение и опыты проводил еще Галилей, поэтому положение о том, что все механические явления в разных ИСО протекают одинаковым образом это называется принципом относительности Галилея.
не изменяется при переходе от одной инерциальной системы отсчета к другой или как говорят они инвариантны по отношению к преобразованию координат, соответствующему переходу от одной инерциальной системы отсчета к другой. Это значит что, с механической точки зрения все инерциальные системы отсчета эквивалентны, ни одной из них нельзя отдать предпочтение перед другими. Практически ни какими опытами нельзя установить находится ли данная ИСО в покое или движется равномерно и прямолинейно. Находясь, например, в вагоне поезда, движущегося равномерно и прямолинейно нельзя установить (не выглянув в окно) движется ли он или находится в состоянии покоя. Мяч в вагоне поезда получит такое же ускорение, как и на Земле при действии одинаковой силы. Свободное падение тел и другие механические процессы будут происходить в вагоне также как если бы он покоился. подобное наблюдение и опыты проводил еще Галилей, поэтому положение о том, что все механические явления в разных ИСО протекают одинаковым образом это называется принципом относительности Галилея.
Энтропия и вероятность
Вместе с тем, все самопроизвольные процессы согласно второго закона в замкнутых макросистемах сопровождаются возрастанием энтропии. Поэтому, между S… Рассмотрим для примера самопроизвольный изотермический процесс расширения газа…– Конец работы –
Используемые теги: Кинетическая, Энергия, вращающ, тела, работа, вращения0.076
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Кинетическая энергия вращающегося тела и работа вращения
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?


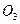
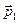
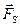
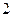
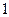

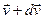






Новости и инфо для студентов