ГЛАВА I. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ

ГЛАВА I. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ

В данной главе решаются системы линейных алгебраических уравнений с использованием матриц и определителей.

§1.1. Определители, некоторые их свойства

Построим хорошо известное из школьного курса решение системы двух уравнений

относительно неизвестных . Решение строим исключением одной из неизвестных. Для этого умножим первое уравнение на, второе на и сложим 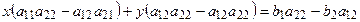, при этом неизвестная исчезает и остается уравнение вида . Аналогичным образом определяем 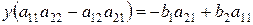. Если выражение , то система имеет единственное решение

.

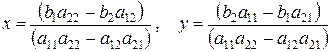Если 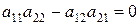, система может не иметь решений (быть несовместной), или иметь бесчисленное множество решений.

Приведенный прием решения задачи можно использовать и при большем числе уравнений и неизвестных, но его реализация становится весьма затруднительной. Для упрощения этого процесса вводятся определители.

Обозначения определителей второго, третьего, четвертого и более высоких порядков:

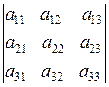, , и так далее.

Определители состоят из элементов, расположенных в строках и столбцах, причем количество строк и столбцов одинаково.

Число строк (столбцов) в определителе называется порядком определителя.

, . Процедура вычисления определителей более высокого порядка будет изложена ниже.

.

Имеют место формулы, позволяющие вычислить определитель любого порядка. Приведем формулы для определителей третьего и четвертого порядков

, (1)

здесь .

,

где

,

.

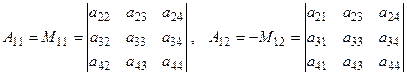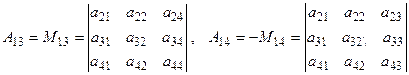Приведенные формулы представляют собой разложение определителей по элементам первой строки. Можно разлагать определитель по элементам любой строки (столбца). Сформулируем еще два свойства определителей.

4) Сумма произведений элементов строки (столбца) на собственные алгебраические дополнения равна значению определителя.

5) Сумма произведений элементов строки на алгебраические дополнения элементов другой строки равна нулю.

Примеры.Вычислить определители1) ,

2)

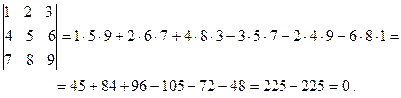
Другой способ (разложение определителя по элементам третьей строки) по формуле (1)

Эти же примеры можно решать с помощью компьютерной системы Maxima. Для этого с помощью команды matrix([15,2],[-7,10]) создадим определитель со строками (15, 2) и (-7,10), затем вычислим этот определитель при помощи команды determinant(matrix([15,2],[-7,10])) и получим ответ 164.

Аналогично determinant(matrix([1,2,3],[4,5,6],[7,8,9]))дает ответ 0.

§1.2. Метод Крамера решения систем линейных алгебраических уравнений

Вернемся к решению системы уравнений

.

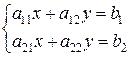Полученное выше решение

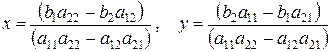
можно записать через определители второго порядка

. (2)

Эти формулы называют формулами Крамера. Они, кстати, справедливы для систем любого порядка.

Определитель, стоящий в знаменателе этих формул, состоит из коэффициентов при неизвестных. Его называют основным определителем системы, поскольку от его значения зависит, совместна ли система уравнений, имеет ли она единственное решение, или их бесчисленное множество. Обозначим его 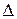. Если принять , то . Это более привычная запись формул Крамера.

Продолжим анализ полученного решения. Формулы Крамера справедливы при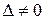и дают единственное решение задачи. Вспомним, что они получены из формул , которые можно использовать и при 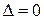. Если 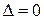, а , то решений уравнения 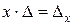, а, следовательно, и системы не существует. Аналогичный результат имеем при 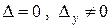. Итак, система несовместна, если 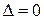, а или .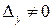

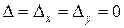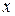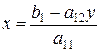Если, то оба уравнения превращаются в тождества при любых значениях и , то есть решений системы бесчисленное множество и определяются они формулой при, или при .

Решим этим же методом систему трех уравнений

.

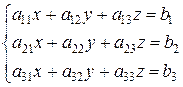Как уже говорилось выше, формулы Крамера работают и в этом случае. Пусть основной определитель системы, составленный из коэффициентов при неизвестных, не равен нулю. Итак, .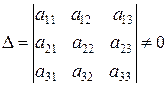

Чтобы получить остальные определители, необходимо подставить столбец свободных членов вместо первого столбца основного определителя, затем вместо второго и третьего. Тогда

,

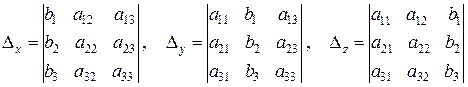а 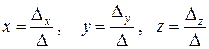. (3)

Пример.Решить методом Крамера систему.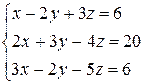

Основной определитель системы уравнений вычисляем по формуле

.

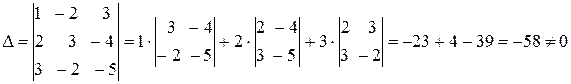Теперь

В соответствии с формулами Крамера (3) . Очевидно, нет смысла вычислять еще один определитель третьего порядка, проще определить с помощью одного из уравнений. Из третьего уравнения следует . Проверим полученный результат, подставив найденные значения неизвестных в первые два уравнения

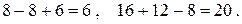
Решим эту же систему также методом Крамера, но с помощью программы Maxima. С помощью команды D: determinant(matrix([1,-2,3],[2,3,-4],[3,-2,-5]))присвоим переменной D значение основного определителя системы, а затем с помощью команд x: determinant(matrix([6,-2,3],[20,3,-4],[6,-2,-5]))/D, y: determinant(matrix([1,6,3],[2,20,-4],[3,6,-5]))/D, z: determinant(matrix([1,-2,6],[2,3,20],[3,-2,6]))/Dвычисляем значения неизвестных.

Примечание. 1) Метод Крамера применим при решении систем практически любого порядка, если число неизвестных совпадает с числом уравнений и основной определитель системы не равен нулю.

2) В случае 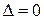метод Крамера приводит к большому количеству вычислений, поэтому чаще всего используются другие методы.

§1.3. Матрицы, некоторые их свойства

В предыдущем параграфе использовалась функция matrix, с помощью которой вводилась таблица коэффициентов. Такого рода таблицы называют матрицами, и они широко используются в линейной алгебре, да и не только. Матрицы могут быть прямоугольными, когда количество строк и столбцов различное, тогда говорят о матрице размера , где число ее строк, а число столбцов. В случае квадратных матриц, у которых число строк и столбцов совпадает, говорят о порядке матрицы. Часто встречаются матрицы-строки и матрицы-столбцы, у первых одна строка, у вторых один столбец.

Замечание. 1) Не следует путать матрицы с определителями. Каждый определитель вычисляется и имеет некоторое значение, возможные действия над определителями описаны выше.

Матрица – это таблица, несущая определенную информацию. Она не вычисляется, законными действиями с матрицами являются лишь те, которые допустимы при работе с объектами, которые исследуются с помощью матриц.

В настоящем курсе матрицы, в основном, используются при решении систем линейных алгебраических и некоторых других уравнений. Отсюда вытекают свойства матриц, о которых буде сказано ниже.

Обозначаются матрицы следующим образом.

матрица размера ,

или

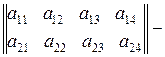матрица размера ,

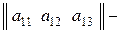матрица-строка, 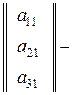матрица-столбец.

Возможно сокращенное обозначение матрицы 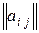, используемое, когда заранее известен ее размер.

Симметричной называют матрицу 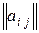, у которой .

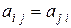Матрицы 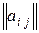и 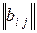равны, если они одного размера и .

Нулевой матрицей называется матрица, все элементы которой нули.

Единичной называют квадратную матрицу, на главной диагонали которой элементы равны 1, все остальные – нули. 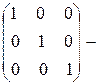единичная матрица третьего порядка.

Рангом матрицы называется порядок максимального, не равного нулю определителя, составленного из элементов матрицы.

Суммой двух матриц одинакового размера называют матрицу, определяемую равенством .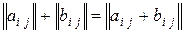

Чтобы умножить матрицу на число, каждый ее элемент нужно умножить на это число.

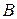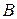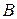Произведение матриц и существует только тогда, когда число столбцов матрицы равно числу строк матрицы , то есть размер матрицы равен , размер матрицы соответственно 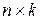, тогда размер матрицы есть .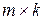

Первый элемент первой строки матрицы равен сумме произведений элементов первой строки матрицы и первого столбца матрицы 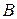, второй элемент первой строки произведения матриц равен сумме произведений элементов первой строки матрицы и второго столбца матрицы 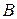и так далее.

Чтобы получить вторую строку матрицы , необходимо вычислить сумму произведений второй строки матрицы с элементами первого, затем второго и так далее столбцов матрицы 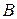. Эта процедура проводится с каждой строкой матрицы . Таким образом, число строк матрицы совпадает с числом строк матрицы , число столбцов с числом столбцов матрицы .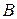

Из правила умножения матриц следует, что, вообще говоря, 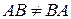, причемможет существовать, а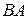нет и наоборот.

Примеры.

1) Вычислить сумму матриц и .

.

2) Умножить матрицу 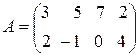на 4.

.

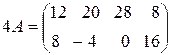3) 3) Вычислить 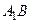, если , .

.

Эти же задачи в программе Maxima решаются с помощью следующих команд. А: matrix([3,5,7,2],[2,-1,0,4]); В: matrix([1,2,4,1],[2,-3,2,4]); А+В; 4*А; А1: matrix([3,5],[2,-1]); А1.В.

§1.4. Метод Гаусса решения систем линейных алгебраических уравнений

Метод решения систем уравнений, применяемый в данном разделе, пригоден для решения систем любого порядка. Демонстрироваться он будет на системах трех уравнений с тремя неизвестными

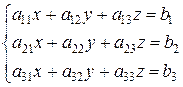
Для данного вида систем вводятся понятия матрицы системы (матрицы коэффициентов системы)

,

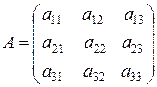и расширенной матрицы, включающей свободные члены системы

.

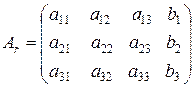Система уравнений совместная, если она имеет хотя бы одно решение. Система, не имеющая решений, называется несовместной.

Совместная система может одно и более решений. Если решений системы более одного, то их бесчисленное множество. Имеет место

Теорема Кронекера-Капелли. Для совместности системы необходимо и достаточно, чтобы ранги матрицы системы и расширенной матрицы 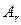совпадали. Ранг в этом случае называют рангом системы уравнений.

Если ранг системы равен числу неизвестных, то система называется определенной и имеет единственное решение. Если ранг системы меньше числа неизвестных, система неопределенная и имеет бесчисленное множество решений.

Метод Гаусса отличается от метода Крамера тем, что он предлагает единый процесс получения решения как совместных, так и несовместных систем уравнений.

Основан метод Гаусса на следующих свойствах систем уравнений.

1) Умножение обеих частей некоторого уравнения системы на не равное нулю число, не меняет ее решения.

2) Если умножить обе части одного из уравнений системы на некоторое число и прибавить полученное уравнение к другому уравнению системы, новая система уравнений будет иметь то же решение, что и исходная.

Иногда системы уравнений, имеющих одинаковое решение, называют эквивалентными или равносильными. Матрицы из коэффициентов эквивалентных систем, можно условно назвать эквивалентными (~) -знак эквивалентности).

Поскольку эквивалентные системы уравнений отличаются только коэффициентами при неизвестных, выгоднее работать не с самими системами, а с матрицами из коэффициентов этих систем.

Продемонстрируем метод Гаусса на системе трех уравнений с тремя неизвестными. Дана система уравнений

,

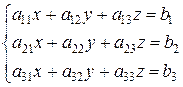Расширенная матрица этой системы уравнений имеет вид

.

Ясно, что матрица несет всю информацию о системе уравнений.

Основная идея метода – приведение матрицы к ступенчатому («треугольному») виду, когда на месте элементов будут стоять нули. Очевидно, последнее уравнение, соответствующее ступенчатой матрице, будет содержать только одну неизвестную (или ни одной), в предыдущем уравнении неизвестных будет две и только в первом уравнении их будет три.

В результате преобразований матрицы получаем

.

Эквивалентной матрице соответствует система уравнений

,

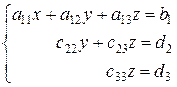причем решение этой системы совпадает с решением исходной системы.

Рассмотрим возможные варианты.

1) пусть 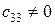, то есть равны нулю только два первых элемента последней строки ступенчатой матрицы, тогда 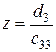, из второго уравнения определяется , из первого 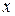. Сюда же входит случай 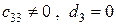, тогда .

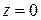2) система несовместна в следующих случаях

2а) если 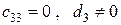, , что невозможно ни при каких ,

2в) при 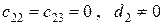. второе уравнение системы не имеет решения.

3) при 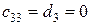, тогда третья строка состоит из нулей, и ранг ступенчатой матрицы, а, следовательно, основной матрицы исходной системы уравнений меньше трех. Как уже говорилось выше, система имеет бесчисленное множество решений. Покажем это. Имеем систему двух уравнений с тремя неизвестными

.

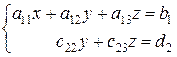3а) Если , то из второго уравнения рассматриваемой системы имеем , после чего из первого уравнения получаем

.

В результате получаем формулы

позволяющие для любого значения определить 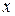и , то есть получить тройку чисел, являющуюся одним из бесконечного множества решений эквивалентной, а следовательно и исходной системы уравнений. Аналогично можно построить и любое другое решение.

3в) При имеем 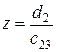, тогда

.

Опять бесчисленное множество решений, для каждого по приведенным формулам определяются 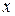и , причем в этом случае для всех троек решений одинаково.

3c) При 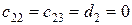имеем еще один вариант бесчисленного множества решений, определяемый формулой

.

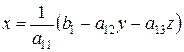Здесь и задаются произвольно, 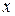определяется из приведенной формулы.

 

Примеры.1) Решить систему уравнений .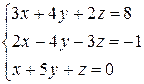

Процедуру приведения данной системы к эквивалентной удобнее осуществлять, когда коэффициент при стоящей слева неизвестной (в нашем случае при 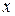) хотя бы в одном уравнении был равен единице, тогда в эквивалентной матрице не появится дробных чисел. Для этого поменяем местами уравнения системы

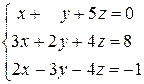
и запишем ее расширенную матрицу

.

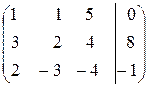Создаем нули во второй и третьей строках первого столбца, для чего умножаем первую строку на 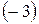и прибавляем ко второй строке, затем умножаем первую же строку на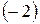и суммируем с третьей строкой, тогда

.

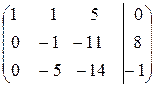Умножаем вторую строку на и прибавляем ее к третьей строке

.

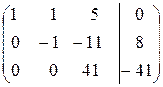Построена ступенчатая матрица, соответствующая исходной расширенной матрице и соответствующая ей система уравнений имеет вид

.

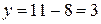Из третьего уравнения имеем , из второго , из первого

. Итак, получено единственное решение данной, а, следовательно, исходной системы уравнений .

Проверка результата .

2) Решить систему уравнений .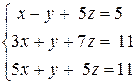

Имеем

.

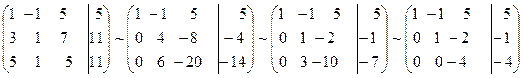В целях упрощения решения при переходе от второй матрицы к третьей вторая и третья строки были поделены на 4 и 2 соответственно.

Запишем систему уравнений, соответствующую полученной матрице

. Очевидно, .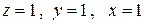

Проверка: .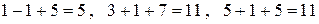

3) Решить систему уравнений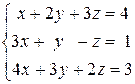

Преобразуем расширенную матрицу системы

.

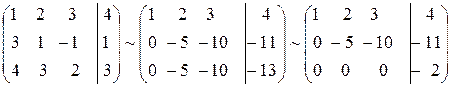Запишем последнее из уравнений, соответствующее полученной расширенной матрице . Это равенство невозможно ни при каких значениях 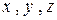, следовательно, эквивалентная система уравнений не имеет решения, и исходная система уравнений также несовместна.

4) Решить систему уравнений .

Тогда

.

Последнее уравнение тождественно выполняется при любых значениях неизвестных, остается система двух уравнений относительно трех неизвестных

.

Из второго уравнения имеем . Из первого уравнения получаем 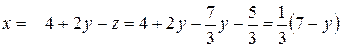. В итоге

.

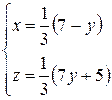Проверка: .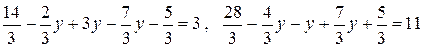

Системы уравнений можно решать с помощью программы Maxima следующим образом.

Вначале определяем ранг основной матрицы системы – матрицы из коэффициентов при неизвестных – с помощью команды rank.

Если ранг этой матрицы совпадает с числом неизвестных, решение системы единственное. Определяем его с помощью команды solve.

Если ранг матрицы меньше числа неизвестных, определяем ранг расширенной матрицы. Когда ранг расширенной матрицы больше ранга основной матрицы, система не имеет решения (несовместна).

Если ранги обеих матриц совпадают, но меньше числа неизвестных, используем команду solve.

Примеры.

1)

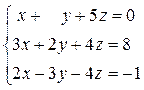
Здесь в качестве иллюстрации приведем целый кусок из компьютерной программы Maxima

Решение единственное.

2)

Решений нет (пустое множество).

3)

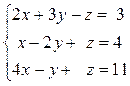
Решений бесчисленное множество.