рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Образование
- /
- Определители 2-го порядка
Реферат Курсовая Конспект
Определители 2-го порядка
Определители 2-го порядка - раздел Образование, Вопрос ...
Вопрос
Определители 2-го порядка
Определителем 2-го порядка является выражение вида:
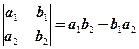 , (1.1)
, (1.1)
где  и
и  - некоторые числа.
- некоторые числа.
Определители 3-го порядка. Правило Саррюса
(1.2)Первые 10 свойств определителя
2) При замене строк или столбцов местами определитель меняет знак: (1.3)Вопрос
Миноры и дополнения
где А11 – алгебраическое дополнение, вычисляемое по общей формуле из минора:Вопрос
Определитель n-го порядка
Метод математической индукции
Теорема: пусть про некоторые свойства высказывания, действующие на некотором промежутке, известно, что где пункт 1 называют базой индукции (И=Истина), а пункт 2 шагом индукции. Вообще, метод математической индукции…Вычисление определителя n-го порядка по минорам и АД
Вычисление определителя n-го порядка по минорам или АД такое же, как и определителя 3-го порядка. Нужно просто учитывать, что при больших порядках определителя, его миноры и дополнения также представляют собой определители, но уже (n-1)-го порядка со своими минорами и АД. Таким образом, вычисление сводится к последовательному понижению порядка исходного определителя с помощью его миноров и АД.
Верхне треугольный определитель
Теорема: ВТО равен произведению элементов его главной диагонали. Все остальные слагаемые, например для определителя 3-го порядка, по правилу Саррюса будут равны нулю. В дальнейшем…Вопрос
А)
Матрицей размера m n называется прямоугольная таблица чисел, состоящих из m строк и n столбцов.
n называется прямоугольная таблица чисел, состоящих из m строк и n столбцов.
Общий вид записи: А= =
=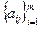
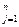

Матрицы называются равными, если они одного порядка и все элементы, стоящие на одних местах, совпадают.
А=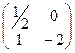 ; В=
; В=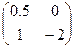 ; А=В.
; А=В.
Замена строк столбцами, а столбцов – строками называется транспонированием матрицы.
Запись: А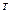 — матрица, транспонированная к матрице А, если А=
— матрица, транспонированная к матрице А, если А=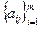
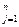 , то А
, то А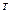 =
= 
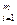 .
.
Сложение матриц
Определение: Если А= , В=, то матрицей А+В будет матрица , а матрицей – матрица . Свойства сложения матриц и умножения матрицы на число: 1. А+В=В+А;Б) Умножение матриц
Тогда произведением матриц А и Вявляется матрица С, число строк которой совпадает с числом строк первого множителя (матрицы А), а число столбцов –… С=АВ; С: mn; , и элементы которой определяются по формуле: Свойства умн. МатрицВопрос
Пусть А=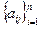
 – квадратная матрица.
– квадратная матрица.
Определение: матрица  называется обратной к матрице А, если выполнено равенство
называется обратной к матрице А, если выполнено равенство 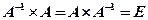 . Отметим, что вырожденная матрица обратной иметь не может, ибо если detA=0 ,
. Отметим, что вырожденная матрица обратной иметь не может, ибо если detA=0 , 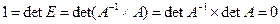 (противоречие).
(противоречие).
Всякая невырожденная матрица А=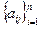
 имеет обратную матрицу
имеет обратную матрицу  = =
= =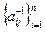
 , элементы которой находят по формуле:
, элементы которой находят по формуле: (5.20)
(5.20)
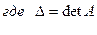 , а
, а 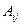 – её алгебраические дополнения.
– её алгебраические дополнения.
Свойства обратной матрицы:
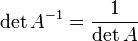
 для любых двух обратимых матриц A и B.
для любых двух обратимых матриц A и B.
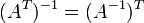 где * T обозначает транспонированную матрицу.
где * T обозначает транспонированную матрицу. 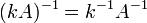 для любого коэффициента
для любого коэффициента 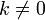 .
.
Алгоритм нахождения обратной матрицы
чтобы найти обратную матрицу  , нужно:
, нужно:
1) найти детерминант матрицы А; если он равен нулю, то обратной нет. Если detA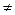 0, то находим
0, то находим
2) матрицу 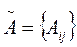 из алгебраических дополнений;
из алгебраических дополнений;
3) транспонируем эту матрицу  ;
;
4) всякий элемент матрицы 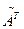 делим на detA, получим матрицу
делим на detA, получим матрицу  .
.
Вопрос.
Системы линейных уравнений
Определение 1) Система (6.1) линейных уравнений называется совместной, если она имеет решения. Определение 2) Система (6.1) называется несовместной, если она не имеет… Определение 3) Система (6.1) называется определенной, если она имеет единственное решение.Матричная форма записи m линейных уравнений с n неизвестными
Положим: 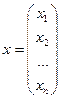 ;
; 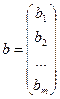 ;
;
Тогда система (6.1) переходит в матричное уравнение:
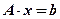 . (6.2)
. (6.2)
(Система линейных уравнений (6.1) эквивалентна одному матричному уравнению (6.2))
Вопрос
Системы n линейных уравнений с n неизвестными их решение с помощью обратной матрицы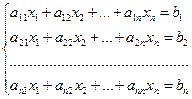 (7.1)
(7.1)
(Система (7.1): n-уравнений с n неизвестными)
Соответствующее матричное уравнение имеет вид:  (7.2)
(7.2)
Если матрица системы А не вырождена, то у нее существует обратная матрица  . Умножая обе части уравнения (7.2) слева на матрицу
. Умножая обе части уравнения (7.2) слева на матрицу  , получим:
, получим: 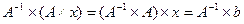 , т.е.
, т.е.
 (7.3)
(7.3)
Мы показали, что справедлива теорема 7.1. Если матрица системы невырожденная, то система определена и её решение можно найти по формуле (7.3). Формула (7.3) даёт решение системы (7.1) с помощью обратной матрицы.
Рассмотрим пример: 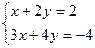 .
.
Матрица системы:  ; тогда обратная матрица (см. пример в §5, п. 5.10):
; тогда обратная матрица (см. пример в §5, п. 5.10): 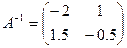 . Тогда из (7.3) имеем:
. Тогда из (7.3) имеем:  , т.е.
, т.е.  = –8;
= –8; 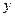 =5
=5
Вопрос.
(8.1) (8.2) Заменим k-й столбец на столбец свободных коэффициентов;Вопрос
Понятие элементарного преобразования
либо 1) замена строк местами; либо 2) умножение строки на число ; либо 3) сложение строк.Эквивалентные матрицы и системы
Соответственно различают эквивалентности первого и второго типа. Системы линейных уравнений называются эквивалентными, если эквивалентны их… Свойства:Ступенчатые матрицы; сведение матрицы к ступенчатой
Ступенчатой называется матрица такого вида: /при переходе к следующей строке «вниз» идем не более, чем на один ненулевой элемент; слева направо последующая строка…Диагональные матрицы
Имеет место следующая теорема: Всякая невырожденная матрица эквивалентна некоторой диагональной и… Теорему доказываем методом математической индукции по порядку матрицы.Вопрос
(Метод Гаусса) Решение произвольной системы линейных уравнений
Системы линейных уравнений называются эквивалентными, если эквивалентны их расширенные матрицы.
Метод Гаусса заключен к сведению расширенной матрицы к ступенчатой.
Рассмотрим его на примере, решая следующую систему: 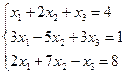

1) Из второй строки вычтем утроенную первую, а из третьей – удвоенную первую;
2) вторую строку поделим на «-11», а третью – на «-3»;
3) к третьей строке прибавим вторую.
Обратный ход:
Матрица 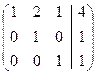 задает следующую систему уравнений
задает следующую систему уравнений 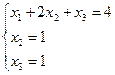
Тогда:  ;
; 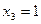 и
и  .
.
Вопрос
Понятие ранга матрицы
Рангом матрицы называется наибольший из порядков отличного от нуля минора матрицы.
При этом под минором матрицы А k-го порядка (обозначение:  ) будем понимать определитель k-го порядка, получаемый из матрицы А в результате вычеркивания некоторых её строк и столбцов.
) будем понимать определитель k-го порядка, получаемый из матрицы А в результате вычеркивания некоторых её строк и столбцов.
Пример:
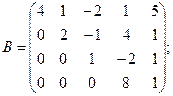
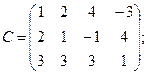
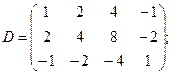

1. Для матрицы А её единственный минор 3-го порядка – 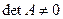 . Поэтому r(A)=3.
. Поэтому r(A)=3.
2. Для матрицы В существует 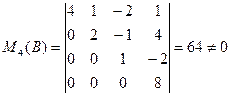 (Получается из В удалением её последнего столбца); поэтому r(В)=4.
(Получается из В удалением её последнего столбца); поэтому r(В)=4.
3. Для матрицы С её третья строка равна сумме первых двух (проверить), и поэтому для всякого её минора третьего порядка третья строка будет равна сумме первых двух, и поэтому он будет равен нулю (см. §1, 9-е свойство определителя третьего порядка).
Тем не менее, есть 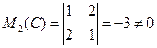 (получаемый из матрицы С удалением её третьей строки и третьего и четвертого столбцов), и поэтому r(С)=2.
(получаемый из матрицы С удалением её третьей строки и третьего и четвертого столбцов), и поэтому r(С)=2.
4. Все строки матрицы D пропорциональны (вторая строка равна удвоенной первой, а третья – первой, взятой с противоположным знаком), и поэтому все миноры второго и третьего порядков содержат пропорциональные строки и равны нулю. Есть лишь 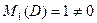 (получается из матрицы D удалением второй и третьей строки, а также второго, третьего и четвертого столбцов), и поэтому r(D)=1.
(получается из матрицы D удалением второй и третьей строки, а также второго, третьего и четвертого столбцов), и поэтому r(D)=1.
В качестве задачи предложим читателю доказать, что имеет место следующая теорема 11.1:
r(A)=1 все строки (и столбцы) матрицы А пропорциональны и А≠0.
все строки (и столбцы) матрицы А пропорциональны и А≠0.
5. В матрице F=0 вообще нет ни одного ненулевого минора; её ранг равен нулю.
Инвариантность ранга при элементарных преобразованиях
Теорема 11.2: Ранг матрицы при элементарных преобразованиях не меняется.
Для её доказательства рассмотрим следующие леммы:
Лемма №1: Пусть r(A)=k, тогда все миноры (k+1)-го порядка 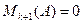 , либо не существуют и
, либо не существуют и 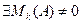 (непосредственно следует из определения ранга).
(непосредственно следует из определения ранга).
Лемма №2: Если 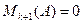 для любого минора, то r(A)≤k.
для любого минора, то r(A)≤k.
Доказательство:
Разлагая минор (k+2)-го порядка матрицы А по какой-либо его строке, мы получим, что он представляется как сумма произведений элементов этой строки на их алгебраические дополнения, каждое из которых, с точностью до знака, совпадает с соответствующим минором (k+1)-го порядка матрицы А, и поэтому равны нулю. Поэтому всякий 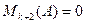 .
.
Разлагая далее любой минор (k+3)-го порядка по некоторой его строке, получим, что он равен сумме произведений элементов его строки на их алгебраические дополнения, которые являются (с точностью до знака) минорами (k+2)-го порядка матрицы А, и поэтому равен нулю. Итак, все 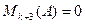 .
.
По аналогии получим, что все  (если они существуют), и лемма №2 доказана.
(если они существуют), и лемма №2 доказана.
Лемма №3: Если r(A)=k, то определитель, состоящий из (k+1)-й строки матрицы А, равен нулю (его получают из минора (k+1)-го порядка с использованием замены строк местами). /она легко следует из леммы №1/
Лемма №4:Любое элементарное преобразование не увеличивает ранга матрицы.
Доказательство:
Пусть r(A)=k, а матрица В получается из матрицы А в результате какого-либо одного из элементарных преобразований строк первого типа (см. §9; лемма для элементарного преобразования строк второго типа будет следовать из её справедливости для элементарных преобразований первого типа, ибо всякое элементарное преобразование строк второго типа можно представить в виде последовательного действия одного или трёх преобразований первого типа).
Рассмотрим каждое из элементарных преобразований строк первого типа последовательно:
1) Замена строк местами: тогда любой 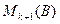 состоит из (k+1)-й строки матрицы А (взятых, возможно, в другом порядке), и поэтому, по лемме №3, он равен нулю.
состоит из (k+1)-й строки матрицы А (взятых, возможно, в другом порядке), и поэтому, по лемме №3, он равен нулю.
2) Умножение строки на число 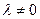 (обозначение:
(обозначение:  – j-я строка матрицы А;
– j-я строка матрицы А;  – j-ю строку матрицы А умножаем на
– j-ю строку матрицы А умножаем на 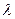 ).
).
Рассмотрим следующие случаи:
а) 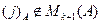 . Тогда в
. Тогда в 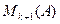 ничего не изменилось, и поэтому, по лемме №1,
ничего не изменилось, и поэтому, по лемме №1,  .
.
б)  . Тогда
. Тогда 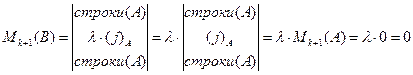 . (см. лемму №1)
. (см. лемму №1)
3) Сложение строк (обозначение:  – j-я строка матрицы В получается сложением (j)-й и (i)-й строк матрицы А). Рассмотрим следующие случаи:
– j-я строка матрицы В получается сложением (j)-й и (i)-й строк матрицы А). Рассмотрим следующие случаи:
а) 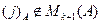 , тогда в
, тогда в 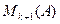 ничего не изменилось, и поэтому, по лемме №1,
ничего не изменилось, и поэтому, по лемме №1,  .
.
б)  . Последние 2 слагаемые являются минорами (k+1)-го порядка матрицы А, которые равны нулю по лемме №1 (во втором слагаемом может быть изменен порядок строк). Поэтому и в этом случае их сумма
. Последние 2 слагаемые являются минорами (k+1)-го порядка матрицы А, которые равны нулю по лемме №1 (во втором слагаемом может быть изменен порядок строк). Поэтому и в этом случае их сумма  .
.
в) 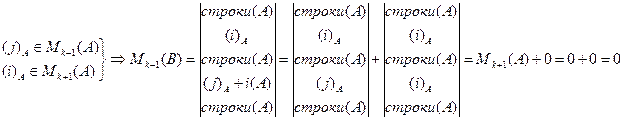 , ибо первое слагаемое в предпоследней сумме является минором (k+1)-го порядка матрицы А, который равен нулю по лемме №1 (r(A)= k), а второй определитель обращается в ноль, так как он имеет одинаковые строки (на месте его i-й и j-й строк находится одна и та же i-я строка матрицы А).
, ибо первое слагаемое в предпоследней сумме является минором (k+1)-го порядка матрицы А, который равен нулю по лемме №1 (r(A)= k), а второй определитель обращается в ноль, так как он имеет одинаковые строки (на месте его i-й и j-й строк находится одна и та же i-я строка матрицы А).
Мы показали, что для любого из элементарных преобразований любой  , и поэтому, по лемме №2, r(B)≤k=r(A). (11.1)
, и поэтому, по лемме №2, r(B)≤k=r(A). (11.1)
Из леммы №4 легко следует
Лемма №5: Пусть из матрицы В получается матрица А конечным числом элементарных преобразований. Тогда r(B)≤r(A) (11.2)
Проведя обратные элементарные преобразования (от В к А), из леммы №5 получим, что r(А)≤r(В) (11.3)
Сопоставляя неравенства (11.2) и (11.3), имеем, что r(А)=r(В), и теорема 11.2 (об инвариантности ранга матрицы) доказана.
Вопрос
Ступенчатые матрицы и их ранг
Определение ступенчатой матрицы
. Ранг ступенчатой матрицыВопрос
Теорема Кронеккер-Капелли
Формулировка теоремы Кронеккер-Капелли
Для того, чтобы система линейных уравнений была совместна, необходимо и достаточно, чтобы ранг её основной матрицы был равен рангу её расширенной матрицы.
 (13.1)
(13.1)
 ;
; 
Формулировка критерия определенности
Теорема (будет доказана в конце §19): Система линейных уравнений (13.1) определена (имеет единственное решение) тогда и только тогда, когда ранг её матрицы равен рангу её расширенной матрицы и равен числу неизвестных.
Доказательство необходимости теоремы Кронеккер-Капелли
Отметим, что r(B)≥r(A), ибо если r(B)=k, то всякий . Но всякий является минором матрицы В (ибо матрица А является частью матрицы В), и поэтому… Итак, пусть r(А)r(В)=k (тогда r(А)<r(B)). Приведя матрицу В к ступенчатому… При этом (k+1)-я строка матрицы В соответствует уравнению: , которое противоречиво, и, следовательно, система (13.1)…Вопрос
А) вектор как направленный отрезок
Под вектором обычно понимается величины , для задания которых необходимо знать не только их численное значение, но и направленное действие… Величины для задания которых достаточно знать лишь их численное значение…Б)
Сложение векторов
1) Правило параллелограмма.
A C
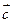 =
= +
+ 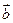




(Векторы а и b не коллинеарные.) 
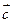
 |
O 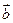 B
B
2) Правило треугольника
С


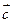 =
= +
+ 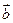
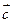
(Векторы а и b могут быть коллинеарные.) 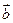
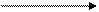 |
О  В
В
Умножение вектора на число
1) ; 2) = |λ| ||; 3)Эти векторы сонаправленны, если λ > 0, и противоположно направлены, если λ < 0.Свойства линейного пространства
2) (+ ) + = + (+) 3) + = 4) + (-) =Ассоциативность
+ = + = + (+) = + = (14.1)Вопрос
А) Линейно – зависимые векторы и их свойства
Определение:
Система векторов 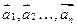 называется линейно-зависимой (л.з.), если
называется линейно-зависимой (л.з.), если  , не все из которых = 0 и
, не все из которых = 0 и  .
.
Определение:
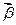 линейно выражается через
линейно выражается через 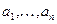 , если
, если 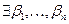 , что
, что 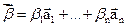
Свойства:
1) Если система содержит нуль-вектор, то она линейно зависима:  =
= 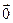 .
.
2) Если система имеет линейно зависимую подсистему, то она линейно зависима.

 , т.к.
, т.к. 
3) Система векторов линейно зависима, тогда и только тогда, когда хотя бы один вектор системы линейно выражается через остальные векторы.
 , если
, если 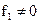 , то
, то 
Если же 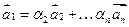 , то
, то 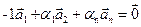 и система
и система  линейно зависима.
линейно зависима.
Б) Формулировки теорем о линейной зависимости коллениарных и компланарных векторов
Теорема 16.1:2 вектора линейно зависимы, тогда и только тогда, когда они коллинеарные. Доказательство: (Смотри п14.2(§14) правило 1) определение)В) Формулировка теоремы о линейной зависимости четырех векторов.
Доказательство: Пусть выходят из общего начала (точки О). Можно считать, что среди векторов… Тогда и, следовательно, (16.1)Вопрос
Линейная зависимость колениарных и компланарных векторов. Линейная зависимость четырех векторов.
Формулировки теорем о линейной зависимости коллениарных и компланарных векторов
Теорема 16.1:2 вектора линейно зависимы, тогда и только тогда, когда они коллинеарные. Теорема 16.2:3 вектора линейно зависимы, тогда и только тогда, когда они…Формулировка теоремы о линейной зависимости четырех векторов.
Теорема 16.3:4 вектора всегда линейно зависимы.
Доказательство теорем
(Смотри п14.2(§14) правило 1) определение) Если , то ( “+”, если сонаправленны; “–“, если противоположно направлены).Вопрос
Исследование систем линейных уравнений
Однородные системы
Ее матричная форма записи есть: (19.2)Решение неоднородных систем
Доказательство:Если – некоторое частное решение системы (19.1), то для любого решения системы (19.7) по теореме 19.1 имеем, что является решением системы… Теорема 19.3 доказана.Доказательство достаточности теоремы Кронеккер-Капелли
где – матрица базисного минора. А так как это матрица невырожденная, то система (19.18) (и система (19.2)) имеет решение. Доказательство критерия определённости системы Если n = r , то по теореме 19.2 множество решений однородной системы (19.7) имеет размерность, равную нулю, то есть…Вопрос
Базис -множество таких векторов в векторном пространстве, что любой вектор этого пространства может быть единственным образом представлен в виде линейной комбинации векторов из этого множества - базисных векторов.
Ортонормированный базис
Определение:Базис является ортогональным, если все его векторы попарно перпендикулярны. Определение:Базис является ортонормированным, если он ортогонален и все…Вопрос
Прямоугольная декартова система координат. Координаты точки. Определение координат вектора по координатам его начала и конца. Расстояние между двумя точками
Координаты точки – это координаты вектора ОМ (где О – начало координат
– это координаты вектора ОМ (где О – начало координат
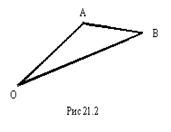
(см. рис 21.1)) , т.е.
, т.е. 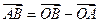 (см. рис. 21.2)
(см. рис. 21.2)
 тогда, если
тогда, если  и
и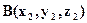 , z
, z
т.е. 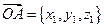 и
и 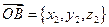 ,
,







 то
то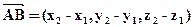
 y
y

x
Рис 21.1
В §24 будет показано, что длина вектора 
 (21.2)
(21.2)
Тогда расстояние между точками A и B:
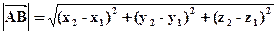 (21.3)
(21.3)
 (расстояние между точками А и В – это длина вектора АВ)
(расстояние между точками А и В – это длина вектора АВ)
Вопрос
Скалярное произведение векторов и его свойства
(23.6) – скалярное произведение Свойства скалярного произведения:Вопрос
Вычисление скалярного произведения векторов через координаты сомножителей
Вычисление скалярного произведения через координаты сомножителей
Ибо 1=и так как Тоесть (24.9)Вычисление угла между векторами
Смотрите формулы (23.6), (24.9), (24.10) Проекция вектора на ось, коллинеарную векторуВопрос
Векторное произведение и его свойства
Определение векторного произведения
при этом , по определению. 1) , 2)Свойства векторного произведения .(антикоммутативность, линейность и однородность)
2. (однородность) 3. и (адютивность (линейность)) Доказательство свойств:Условие коллинеарности двух векторов
Из условия 2 при определении векторного произведения получаем , что
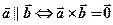 (25.13)
(25.13)
( ибо если  ,параллелограмм OADB (см.рис 25.1) будет иметь нулевую площадь и наоборот)
,параллелограмм OADB (см.рис 25.1) будет иметь нулевую площадь и наоборот)
Векторное произведение базисных ортов
А векторное произведение различных базисных ортов должно быть ортогонально им и иметь единичную длину. ( как площадь квадрата , сторона которого равна длине базисного орта т.е. единице), т.е. такое векторное произведение – это «плюс» или «минус»- третий базисный орт. По правилу правой руки определяем, что
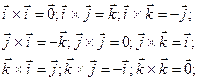
Вопрос
Вычисление векторного произведения через
Координаты сомножителей
Тогда из (25.14) и свойств 2) и 3) векторного произведения следует:Вопрос
Смешанное произведение векторов и его свойство
Определение смешанного произведения
Геометрический смысл смешанного произведения Если > 0, значит векторы образуют правую систему (т.е. имеют такую же… Если < 0, значит векторы образуют левую систему (аналогично для пальцев и ладони левой руки).Свойства смешанного произведения
- циклическая замена не меняет знак.Необходимое и достаточное условие компланарности трех векторов
Доказательство: Если компланарные , то паралелепипед имеет нулевой объем (см. Рис 27.1)т.е.…Вопрос
Смешанное произведение векторов в координатной форме
(см. (24.9)и (26.1))Вопрос
А)
Уравнение плоскости по точке и нормали
Определение 36.1. Плоскостью будем называть геометрическое место точек, такое что, при некотором ненулевом векторе  для всех точек
для всех точек  и
и 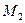 из данного множества вектор
из данного множества вектор  ортогонален заданному вектору.
ортогонален заданному вектору.
Определение 36.2. Вектор  , заданный в определении 36.1, называется нормалью (или нормальным вектором) к заданной плоскости.
, заданный в определении 36.1, называется нормалью (или нормальным вектором) к заданной плоскости.
(Определение 36.1 геометрически означает, что если прямая линия, имеющая направляющий вектор , перпендикулярный плоскости  , то она ортогональна любой прямой , лежащей в этой плоскости.)
, то она ортогональна любой прямой , лежащей в этой плоскости.)
Получим общее уравнение плоскости.
Пусть нормаль 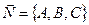 . Так как
. Так как 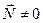 , то
, то
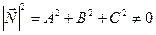 (36.1)
(36.1)
Положим, 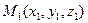 - некоторая точка плоскости. Тогда для любой точки
- некоторая точка плоскости. Тогда для любой точки 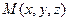 из плоскости
из плоскости  вектор
вектор  , по определению 36.1, ортогонален вектору
, по определению 36.1, ортогонален вектору  , т.е. их скалярное произведение
, т.е. их скалярное произведение
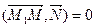 (36.2)
(36.2)
Выписывая равенство (36.2) покоординатно (из §21 вектор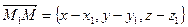 , из равенства (24.9) имеем:
, из равенства (24.9) имеем:
 (36.3)
(36.3)
Раскрывая скобки в равенстве (36.3) и обозначив за  ,
,
получим:
 (36.4)
(36.4)
С условием  (36.1)
(36.1)
Мы показали, что координаты всех точек любой плоскости удовлетворяют некоторому линейному уравнению (36.4) с условием (36.1)
Покажем обратное, т.е. если координаты всех точек некоторого множества  удовлетворяют линейном уравнению (36.4) с условием (36.1) то это множество является плоскостью.
удовлетворяют линейном уравнению (36.4) с условием (36.1) то это множество является плоскостью.
Отметим, что данное множество π≠Ø, ибо если 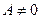 (см.(36.1)) то точка с координатами
(см.(36.1)) то точка с координатами 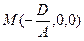 удовлетворяет уравнению (36.4)
удовлетворяет уравнению (36.4)
Тогда пусть 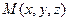 и
и 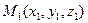 - произвольные точки множества
- произвольные точки множества  , т.е. их координаты удовлетворяют (36.4) и следующему уравнению (для точки
, т.е. их координаты удовлетворяют (36.4) и следующему уравнению (для точки  )
)
 (36.5)
(36.5)
Вычитая из уравнения (36.4) равенство (36.5), получим формулу (36.3), что означает, что вектора  и
и 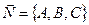 ( из условия (36.1)), следует,что вектор
( из условия (36.1)), следует,что вектор 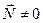 ) удовлетворяет равенству (36.2), т.е они ортогональны. Поэтому выполняются все условия определения 36.1, т.е. множество
) удовлетворяет равенству (36.2), т.е они ортогональны. Поэтому выполняются все условия определения 36.1, т.е. множество  , координаты всех точек которого удовлетворяют некоторому линейному уравнению (36.4) с условием (36.1), является плоскостью.
, координаты всех точек которого удовлетворяют некоторому линейному уравнению (36.4) с условием (36.1), является плоскостью.
Определение 36.4. Поэтому уравнение (36.4) с условием (36.1) называется общим уравнением плоскости.
Б)
Общее уравнение плоскости и его исследование
1.A=0. Тогда уравнение плоскости примет вид: Эта плоскость имеет вид нормаль , т.е. она ортогональна векторуВопрос
Условия параллельности и перпендикулярности двух плоскостей, угол между ними
Взаимное расположение двух плоскостей
Даны плоскости: : (37.1) : (37.2)Угол между двумя плоскостями
: ; ={A2,B2,C2} – её вектор нормали. Угол между двумя плоскостями совпадает с углом между их нормалями (см.рис 37.1), т.е = (37.4)Условие перпендикулярности
n2Вопрос
А)
Уравнение плоскости, проходящей через заданную точку и ортогональной заданному вектору
Пусть дана плоскость 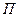 :
: 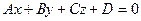
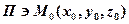 ;
;  ,
, 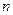 – её вектор нормали
– её вектор нормали
Тогда уравнение такой плоскости было получено в §36, и оно имеет вид:  (36.3)
(36.3)
Уравнение плоскости, проходящей через заданную точку и коллинеарной двум заданным неколлинеарным векторам
Б)
Уравнение плоскости, проходящей через две заданные точки и коллинеарной заданному ненулевому вектору
Тогда векторы (М (x,y,z)- произвольная точка на плоскости ) компланарны, т.е.В)
Уравнение плоскости, проходящей через три заданные точки
. Это уравнение имеет вид: (38.4)Г)
Уравнение плоскости в отрезках
Вопрос
Расстояние от точки до плоскости
Расстояние от точки до плоскости вычисляется по формуле (эта формула доказывается в параграфе 44) (39.1) Пусть ,, , тогда нормальное уравнение плоскости: , (39.2)Вопрос
Прямая как пересечение двух плоскостей.
Общее уравнение прямой в пространстве
– общее уравнение прямой в пространстве, где (40.1) : , : , .Каноническое уравнение прямой как уравнение прямой в пространстве проходящей через заданную точку и коллинеарной заданному вектору
рис 40.1 , Пусть M(x,y,z) – точка прямой L Тогда , т.е. имеет местоПараметрическое уравнение прямой в пространстве
(40.3) Выразим x, y, z в (40.3) через tВопрос
Приведение общего уравнения прямой к каноническому виду
: Условие (40.1) легко можно переписать в виде (41.1)Вопрос
Уравнение прямой в пространстве, проходящей через две заданные точки
Каноническое уравнение этой прямой имеет вид: ; (42.1) а её параметрическое уравнение:Вопрос
А)
Взаимное расположение двух прямых в пространстве
, , , , Рассмотрим матрицыБ)
Угол между двумя прямыми  и
и  можно найти как угол между их направляющими векторами
можно найти как угол между их направляющими векторами 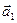 и
и 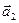 , которые, согласно равенству (24.11) (см.§24), можно найти по формуле:
, которые, согласно равенству (24.11) (см.§24), можно найти по формуле:
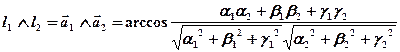 (43.5)
(43.5)
Условие ортогональности и перпендикулярности прямых
 . Для перпендикулярности прямых
. Для перпендикулярности прямых  и
и  (
(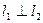 и
и 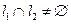 ) к последнему условию надо добавить также равенство (43.3).
) к последнему условию надо добавить также равенство (43.3).
Вопрос
А)
Взаимное расположение прямой и плоскости
прямая , , (-направляющий вектор прямой , а - одна из её точек) : , (- нормаль к плоскости )Б)
Угол между прямой и плоскостью. Условие их перпендикулярности
= Мы показали (44.4)Точка пересечения прямой и плоскости
(37.3) то для того, чтобы найти точку пересечения прямой с плоскостью : Ax+By+Cz+D=0 (36.4)Вопрос
Расстояние от точки до прямой в пространстве
Расстояние от точки M1 до прямой L() совпадает с высотой () параллелограмма (см. рис 45.1), которая равна отношению площади () этого…Вопрос
Расстояние между скрещивающимися прямым
Вопрос
А) эллипсоид
(47.17) При этом отрезки [0,a],[0,b] и [0,c] по осям абсцисс, ординат и аппликат… Эллипсоид -центральная поверхность; для эллипсоида, заданного уравнением (47.17), начало координат является его…Б) Однополостный гиперболоид
(47.18) Общий вид однополостного гиперболоида изображён на рис. 47.4 Если мы будем вращать гиперболу вокруг непересекающей её оси симметрии, то получим однополостной гиперболоид вращения…В) Двуполостный гиперболоид
(47.20) Общий вид двуполостного гиперболоида изображён на рис.47.7Г) Эллиптический параболоид
Эллиптическим параболоидом называется поверхность, координаты всех точек которой в некоторой системе координат удовлетворяют уравнению:
 (47.24)
(47.24)

Рис 47.10 Рис.47.11 Рис.47.12
Общий вид эллиптического параболоида изображён на рис.47.10, при этом начало координат (для уравнения (47.24)) будет вершиной параболоида, а ось аппликат OZ(являющаяся его осью симметрии, что легко проверить, ибо если точка  лежит на эллиптическом параболоиде, т.е. её координаты
лежит на эллиптическом параболоиде, т.е. её координаты  удовлетворяют уравнению (47.24), то и координаты симметричной ей относительно оси аппликат точки
удовлетворяют уравнению (47.24), то и координаты симметричной ей относительно оси аппликат точки  также удовлетворяют уравнению (47.24), т.е. эта симметричная точка также находится на эллиптическом параболоиде) является осью эллиптического параболоида.
также удовлетворяют уравнению (47.24), т.е. эта симметричная точка также находится на эллиптическом параболоиде) является осью эллиптического параболоида.
Эллиптический (точнее - круговой) параболоид вращения получится, если мы параболу будем вращать вокруг её оси симметрии (см.рис. 47.11)
В сечении эллиптического параболоида плоскостями могут получиться:
-парабола (если секущая плоскость параллельна оси параболоида или проходит через неё; исходя из рис.47.12 читателю предлагаем самостоятельно доказать, что в сечении эллиптического параболоида такой плоскостью будет некоторая неограниченная непрерывная кривая второго порядка, т.е. парабола);
-эллипс (когда секущая плоскость не параллельна его оси, пересекает, но не касается эллиптического параболоида; читателю предлагает показать самостоятельно, исходя из рис. 47.12, что в этом случае в сечении возникает некоторая ограниченная кривая второго порядка, т.е. эллипс);
-одна точка(если плоскость касается эллиптического параболоида);
-пустое множество(когда плоскость не пересекает эллиптический параболоид).
Остальные линии в сечении эллиптического параболоида плоскостями получить нельзя.
Д) Гиперболический параболоид
(47.25) Гиперболический параболоид имеет вид «седла», и его общий вид показан на рис.…Е) Цилиндрические поверхности второго порядка
Существует такая прямая линия , что для всякой точки , лежащей на заданной поверхности, вся прямая, параллельная и проходящая через точку , также… Определение 47.7 Прямая в определении 47.6 называется образующейцилиндрической… Подходящим образом подобрав систему координат, можно считать, что образующая цилиндрической поверхности параллельна…Эллиптический цилиндр
II. Гиперболический цилиндр
(34.1) Общий вид гиперболического цилиндра изображён на рис.47.17III. Параболический цилиндр
(34.3) Общий вид параболического цилиндра изображён на рис. 47.18. В сечении параболического цилиндра плоскостями могут получаться:Ж) Конус второго порядка
(47.8) Отметим, что если координаты точки удовлетворяют уравнению (47.8), то и для… Поэтому, если точка лежит на конусе (47.8), то и вся прямаяЗ) Распадающиеся и вырожденные поверхности второго порядка
Определение 47.16.Поверхность второго порядка называется распадающейся, если она состоит из двух поверхностей первого порядка. В качестве примера рассмотрим поверхность, заданную уравнением (35.21)И) Классификация поверхностей второго порядка

 -эллипсоид
-эллипсоид
-однополостной гиперболоид Основные
-двуполостной гиперболоид поверхности
-эллиптический параболоид второго
-гиперболический параболоид порядка

 -эллиптический цилиндр цилиндрические поверхности
-эллиптический цилиндр цилиндрические поверхности
-гиперболический цилиндрвторого порядка
 -параболический цилиндр
-параболический цилиндр
 -конус второго порядка
-конус второго порядка

 -две пересекающиеся плоскости распадающаяся
-две пересекающиеся плоскости распадающаяся
-две параллельные плоскости поверхность
 -одна плоскость второго порядка
-одна плоскость второго порядка

 -одна прямая линия
-одна прямая линия
-одна точка вырожденные
-пустое множества (мнимый эллипсоид поверхности
мнимый эллиптический цилиндр,
 мнимые параллельные плоскости)
мнимые параллельные плоскости)
Читателю предлагается самостоятельно установить, что все выше перечисленные 15 множеств являются уникальными, т.е. для любой пары из вышеперечисленных множеств никакую поверхность из заданной пары нельзя перевести в другую поверхность из той же пары никаким линейным преобразованием координат. Для этого для заданной пары поверхностей (легко видеть, что только из основных поверхностей второго порядка можно составить 36 пар) надо найти линию второго порядка, которую можно получить в сечении плоскостями одной из поверхностей заданной пары, но нельзя получить в сечении плоскостью другой из поверхностей из этой пары. Впрочем, для распадающихся и вырожденных поверхностей второго порядка это достаточно очевидно, ибо всякое невырожденное линейное преобразование координат плоскость может перевести только
в плоскость, линии их пересечения – в линию их пересечения, прямую линию – в прямую линию, одну точку – в одну точку, а пустое множество – в пустое множество.
– Конец работы –
Используемые теги: определители, 2-го, порядка0.062
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Определители 2-го порядка
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов