рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Численные методы решения краевых задач для уравнений математической физики.
Реферат Курсовая Конспект
Численные методы решения краевых задач для уравнений математической физики.
Численные методы решения краевых задач для уравнений математической физики. - раздел Математика, Московский Государственный Институт Электр...
Московский Государственный Институт Электронной Техники
(Технический Университет)
Кафедра высшей математики - 1
Курсовая работа
по курсу «Численные методы»
Численные методы решения краевых задач для уравнений математической физики.
Вариант 81.
Выполнил:
Студент группы МП-32 Кузин К.С.
Преподаватель:
Хахалин С.Я.
Москва 2008 г.

Содержание
1.кЛАССИФИКАЦИЯ УРАВНЕНИЯ, ФИЗИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ЗАДАЧИ 3
2. Метод сеток, сеточные функции, сеточные пространства 5
3. Вычислительные схемы решения сеточных уравнений 5
4. явная разностная схема для волнового уравнения 5
4.1. Аппроксимация дифференциального уравнения. 5
4.2. Аппроксимация 1-го начального условия. 6
4.3. Аппроксимация 2-го граничного условия. 6
4.4. Аппроксимация 2-го начального условия. 6
4.5. Аппроксимация 1-го граничного условия. 6
4.6. Аппроксимация решения. 7
4.7. Устойчивость решения. 8
4.8. Сходимость решения. 8
5. неявная разностная схема для волнового уравнения 8
5.1. Аппроксимация дифференциального уравнения. 8
5.2. Аппроксимация начальных условий. 9
5.3. Аппроксимация 2-го граничного условия. 9
5.4. Аппроксимация 1-го граничного условия. 9
5.5. Определение прогоночных коэффициентов. 10
5.6. Исследование схемы. Устойчивость. 11
6. Практическая область применимости явной и неявной схем 12
7. исследование сходимости решения по сетке 13
8. решение модельной задачи 13
9. Результаты работы программы 15
10. текст программы 24
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ 36
1. Классификация уравнения, физическая интерпретация задачи.

Данное неоднородное линейное дифференциальное уравнение в частных производных второго порядка является уравнением продольных колебаний струны. Рассмотрим струну длиной 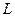 . Положение каждой точки струны характеризуется значением абсциссы
. Положение каждой точки струны характеризуется значением абсциссы 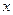 .
.  - вертикальное отклонение струны в точке
- вертикальное отклонение струны в точке 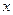 в момент времени
в момент времени  от положения равновесия.
от положения равновесия.
Для выделения единственного решения задачи для дифференциального уравнения необходимы дополнительные условия. Условия, поставленные при t=0, называются начальными. Условия, поставленные на границе области изменения пространственной переменной, называют граничными или краевыми. Рассматриваем задачу в прямоугольной области изменения переменных  . Начальные и граничные условия определяют решение уравнения колебаний струны
. Начальные и граничные условия определяют решение уравнения колебаний струны  , где
, где 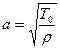 ,
,  - натяжение струны,
- натяжение струны, 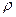 - плотность материала струны.
- плотность материала струны.
Начальные значения  и
и  задают начальную форму струны и распределение скоростей в начальный момент времени. Граничное условие первого рода (условие Дирихле)
задают начальную форму струны и распределение скоростей в начальный момент времени. Граничное условие первого рода (условие Дирихле)  определяет закон движения правого конца струны – условие «свободного конца». Для левого конца в качестве граничного условия задано условие второго рода (условие Неймана)
определяет закон движения правого конца струны – условие «свободного конца». Для левого конца в качестве граничного условия задано условие второго рода (условие Неймана)  . Функция
. Функция  имеет смысл плотности внешней силы, рассчитанной на единицу длины.
имеет смысл плотности внешней силы, рассчитанной на единицу длины.
Сформулируем первую краевую задачу для уравнения колебаний струны: найти функцию  , определенную в области
, определенную в области  , удовлетворяющую уравнению
, удовлетворяющую уравнению  , а также начальным и граничным условиям.
, а также начальным и граничным условиям.
Рассмотрим канонический вид уравнения гиперболического типа:
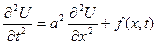 ,
,  .
.
Проведем замену переменных:  . В новых переменных уравнение приобретает вид:
. В новых переменных уравнение приобретает вид:
 ,
,  .
.


Если считать 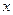 и
и  уже преобразованными переменными, то задача принимает вид:
уже преобразованными переменными, то задача принимает вид:
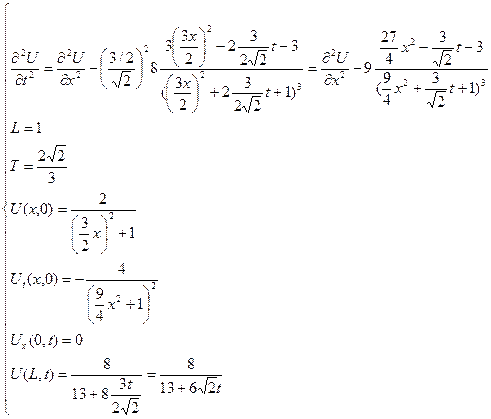
Метод сеток, сеточные функции и сеточные пространства.
Метод сеток состоит в сведении решения краевой задачи к решению системы алгебраических уравнений для так называемой сеточной функции. Для этого…Вычислительные схемы решения сеточных уравнений.
Применение конечно-разностного метода для решения краевой задачи приводит в общем случае к системе линейных алгебраических уравнений для сеточных… В явной схеме значение сеточной функции на последующем слое определяется…Явная разностная схема для волнового уравнения.
4.1. Аппроксимация дифференциального уравнения.
Для сведения задачи к явной разностной схеме используем шаблон «крест»:

Получаем конечно-разностную схему:
 . (1)
. (1)
Обозначим  и выразим
и выразим 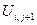 через остальные значения сеточной функции, входящие в уравнение:
через остальные значения сеточной функции, входящие в уравнение:
 . (2)
. (2)
Это уравнение должно выполняться для всех внутренних узлов сетки. Для того чтобы система стала полностью определенной, необходимо дополнить ее уравнениями, получаемыми из аппроксимации краевых и начальных условий.
4.2. Аппроксимация первого начального условия: 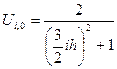 ,
,  .
.
4.3. Аппроксимация второго граничного условия:  ,
,  .
.
4.4. Аппроксимация второго начального условия.
Для этого разложим  в окрестности точки
в окрестности точки  по формуле Тейлора:
по формуле Тейлора:
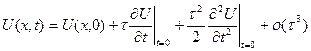 .
.
Используя начальные условия:
 . (*)
. (*)
Перейдем к конечным разностям, записываемым в узле  (т.е. на первом слое):
(т.е. на первом слое):
 . (3)
. (3)
Данная формула используется на начальном этапе для вычисления функции 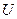 на первом слое по известным значениям функции
на первом слое по известным значениям функции 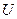 на нулевом слое и на границе. После того как значения
на нулевом слое и на границе. После того как значения  для
для  и
и  определены, включается рекуррентная процедура (2) и вычисляется
определены, включается рекуррентная процедура (2) и вычисляется 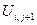 .
.
4.5. Аппроксимация первого граничного условия.
Запишем формулу (3) при  :
:
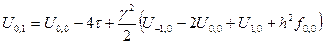 .
.
Выразим 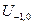 :
:
 . (4)
. (4)
Запишем формулу (1) при  и
и  :
:
 .
.
Выразим 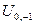 :
:
 . (5)
. (5)
Теперь подставим выражение (4) для 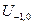 в (5):
в (5):
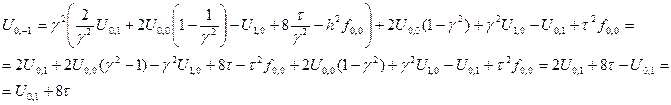 Разложим
Разложим  в окрестности точки
в окрестности точки 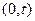 по формуле Тейлора:
по формуле Тейлора:
 .
.
Используя начальные условия:
 . (**)
. (**)
Перейдем к конечным разностям, записываемым в узле 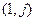 :
:
 . (6)
. (6)
При  (6) имеет вид:
(6) имеет вид:
 . (7)
. (7)
Подставляем выражение 
 в (7):
в (7):


Теперь получим выражение для  :
:
 .
.
Выразим 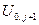 из (6):
из (6):
 .
.
Получим значения  для
для  .
.
После того, как выбраны формулы (*) и (**), разностное решение существует и единственно.
4.6. Аппроксимация решения.
Разложим точное решение по формуле Тейлора с центром в узле  , предполагая наличие непрерывных четвертых производных:
, предполагая наличие непрерывных четвертых производных:


Используя эти разложения, находим невязку схемы:

И невязку начального  и граничного
и граничного  условий
условий
 ,
,
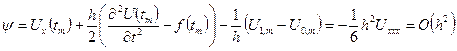 .
.
Начальное  и краевое
и краевое  условия аппроксимируются точно. Таким образом, схема имеет аппроксимацию
условия аппроксимируются точно. Таким образом, схема имеет аппроксимацию  .
.
4.7. Устойчивость решения.
Исследуем устойчивость схемы, полагая  ,
,  .
.

Для множителя роста гармоники получим квадратное уравнение:
 .
.
По теореме Виета произведение его корней  . Значит, условие устойчивости
. Значит, условие устойчивости  может быть выполнено, если
может быть выполнено, если  . Для уравнения с действительными коэффициентами это означает, что корни образуют комплексно сопряженную пару. Для этого дискриминант уравнения не должен быть положительным:
. Для уравнения с действительными коэффициентами это означает, что корни образуют комплексно сопряженную пару. Для этого дискриминант уравнения не должен быть положительным:
 .
.
Чтобы неравенство выполнялось для любых гармоник, необходимо и достаточно соблюдение условия Куранта:  . Таким образом, схема «крест» условно устойчива.
. Таким образом, схема «крест» условно устойчива.
Несмотря на очевидную простоту вычислительной процедуры, характерной для явной схемы, ее практическая реализация возможна при таких соотношениях между шагами сетки 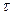 и
и 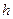 , при которых выполняется условие устойчивости решения к ошибкам округления и неточностям в начальных данных. Для уравнения гиперболического типа это условие имеет вид:
, при которых выполняется условие устойчивости решения к ошибкам округления и неточностям в начальных данных. Для уравнения гиперболического типа это условие имеет вид:  (условие Куранта - Леви). Если условие устойчивости разностной схемы не будет выполнено, то в процессе рекуррентного решения возможно накапливание ошибок от слоя к слою, что приведет к неудовлетворительному результату, несмотря на высокую точность аппроксимации дифференциальной краевой задачи разностной схемой. На практике стараются использовать неявные схемы, то есть такие, которые не могут быть сведены к рекуррентным формулам. Значения сеточной функции
(условие Куранта - Леви). Если условие устойчивости разностной схемы не будет выполнено, то в процессе рекуррентного решения возможно накапливание ошибок от слоя к слою, что приведет к неудовлетворительному результату, несмотря на высокую точность аппроксимации дифференциальной краевой задачи разностной схемой. На практике стараются использовать неявные схемы, то есть такие, которые не могут быть сведены к рекуррентным формулам. Значения сеточной функции  на каждом данном слое в таких схемах получают путем решения системы линейных алгебраических уравнений специального вида.
на каждом данном слое в таких схемах получают путем решения системы линейных алгебраических уравнений специального вида.
4.8. Сходимость решения.
Схема с данными начальными условиями при выполнении условия Куранта – Леви сходится со скоростью  .
.
Неявная разностная схема для волнового уравнения.
5.1. Аппроксимация дифференциального уравнения.
Для аппроксимации уравнения используем Т-образный пятиточечный шаблон:

Уравнение аппроксимируется следующей системой разностных уравнений:
 ,
,  ,
,  (8)
(8)
с погрешностью аппроксимации  .
.
5.2. Аппроксимация начальных условий.
Начальные условия аппроксимируем с порядком  аналогично тому, как это делалось для явной схемы:
аналогично тому, как это делалось для явной схемы:
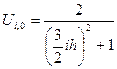 ,
, 
 . (9)
. (9)
Здесь отличие заключается в том, что  аппроксимируется разностной производной второго порядка на первом слое, а не на нулевом, как в случае явной схемы.
аппроксимируется разностной производной второго порядка на первом слое, а не на нулевом, как в случае явной схемы.
Запишем (8) следующим образом:
 ,
,  ,
,  (10)
(10)
Равенство (9) запишем в такой же форме:
 ,
,  (11)
(11)
5.3. Аппроксимация второго граничного условия:  ,
,  .
.
5.4. Аппроксимация первого граничного условия.
Для получения погрешности аппроксимации порядка  запишем выражение для центральной разности в узле
запишем выражение для центральной разности в узле  (метод фиктивного узла):
(метод фиктивного узла):


Разложим  в окрестности точки
в окрестности точки  по формуле Тейлора:
по формуле Тейлора:
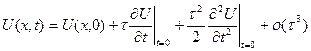 .
.
Используя начальные условия:
 .
.
Перейдем к конечным разностям, записываемым в узле  (т.е. на первом слое):
(т.е. на первом слое):
 .
.
При 
 .
.


С учетом  :
:
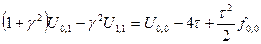 .
.
Полученное уравнение для слоя  рассматривается как первая строка трехдиагональной системы уравнений, которая решается методом прогонки.
рассматривается как первая строка трехдиагональной системы уравнений, которая решается методом прогонки.
Для  :
:  . Предполагая достаточную гладкость искомого решения, аппроксимируем волновое уравнение в узле
. Предполагая достаточную гладкость искомого решения, аппроксимируем волновое уравнение в узле 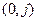 :
:
 . (12)
. (12)
С учетом  :
:
 . (13)
. (13)
А данное уравнение рассматривается как первая строка трехдиагональной системы уравнений, решаемой прогонкой по слоям, начиная с  .
.
Таким образом, построена неявная разностная схема аппроксимирующая краевую задачу с погрешностью аппроксимации порядка  . В левую часть уравнений (10) - (13) входят в качестве неизвестных три значения сеточной функции в трех соседних узлах j+1-ого слоя, поэтому такая разностная схема называется неявной. Полученная система линейных алгебраических уравнений описывается трехдиагональной матрицей. Для решения таких систем применяется метод прогонки.
. В левую часть уравнений (10) - (13) входят в качестве неизвестных три значения сеточной функции в трех соседних узлах j+1-ого слоя, поэтому такая разностная схема называется неявной. Полученная система линейных алгебраических уравнений описывается трехдиагональной матрицей. Для решения таких систем применяется метод прогонки.
5.5. Определение прогоночных коэффициентов.
Найдем  при
при  . Пусть
. Пусть 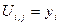 . Тогда трехдиагональная система имеет вид:
. Тогда трехдиагональная система имеет вид:



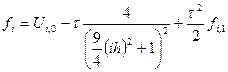
Граничные прогоночные коэффициенты:
 ;
;  ;
;
 ;
;  ;
; 
Теперь, зная значения при  находим
находим  , где
, где  . Трехдиагональная матрица имеет вид:
. Трехдиагональная матрица имеет вид:


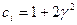

Граничные прогоночные коэффициенты:
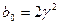 ;
;  ;
; 
 ;
;  ;
; 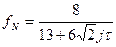
Проверка корректности и устойчивости метода прогонки. Для  и
и  выполнены следующие условия:
выполнены следующие условия: 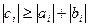 ,
,  ,
,  . Тогда для алгоритма имеют место равенства
. Тогда для алгоритма имеют место равенства  ,
,  , гарантирующие корректность и устойчивость метода прогонки.
, гарантирующие корректность и устойчивость метода прогонки.
5.6. Исследование схемы. Устойчивость.
Значения решения на нулевом и первом слоях вычисляют, как при использовании явной схемы. На остальных слоях схема с краевыми условиями образует относительно  линейную систему уравнений с трехдиагональной матрицей, в которой диагональные элементы преобладают. Решение этой системы существует, единственно и вычисляется методом прогонки.
линейную систему уравнений с трехдиагональной матрицей, в которой диагональные элементы преобладают. Решение этой системы существует, единственно и вычисляется методом прогонки.
Разложение решения по формуле Тейлора нетрудно установить, что на решениях с непрерывными четвертыми производными схема аппроксимирует уравнение с погрешностью  .
.
Устойчивость проверяется методом разделения переменных. Данный пятиточечный шаблон является частным  случаем неявной разностной схемы с весами при пространственных производных на разных слоях:
случаем неявной разностной схемы с весами при пространственных производных на разных слоях:
 ,
,
 ,
,
чтобы все веса были неотрицательны, следует брать  . Делая аналогичную подстановку, получим для множителя роста квадратное уравнение
. Делая аналогичную подстановку, получим для множителя роста квадратное уравнение
 .
.
На основании тех же рассуждений можно сделать следующий вывод: устойчивость будет только при комплексно сопряженных корнях, т.е. при  . Отсюда вытекает условие устойчивости схемы:
. Отсюда вытекает условие устойчивости схемы:
 .
.
Из данного неравенства видно, что при 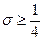 схема безусловно устойчива. Если
схема безусловно устойчива. Если  , то схема условно устойчива при
, то схема условно устойчива при  , т.е. неявная схема сходится с точностью
, т.е. неявная схема сходится с точностью  при условии
при условии  .
.
Практическая область применимости явной и неявной схем.
Используя неявную схему, можно находить негладкие решения разностным методом. Многие задачи математической физике, описывающие ударные процессы в…Исследование сходимости решения по сетке.
При исследовании сходимости решения воспользуемся следующим методом: возьмем начальную сетку и вычислим значения сеточной функции в узлах этой… Изменение количества узлов 10 - 20 20 - 50 …Решение модельной задачи.
Результаты работы программы.
>>main РЕШЕНИЕ УРАВНЕНИЯ КОЛЕБАНИЙ Решения, полученные с использованием явной и неявной схем при 50 узлах на пространственной и временной осяхТекст программы.
Fun_graph.m
%Параметры N1, N2 - количество узлов по осям x и t function [U,U_n] = fun(N1,N2) %Задание границ области дискретного изменения аргументаFun.m
%Функция расчета сеточной функции с использованием явной и неявной схем
%Параметры N1, N2 - количество узлов по осям x и t
function [U,U_n] = fun(N1,N2)
%Задание границ области дискретного изменения аргумента
L_const=1;
T_const=2^(3/2)/3;
x_begin=0;
x_end=L_const;
t_begin=0;
t_end=T_const;
%Определение шага по осям x и t
h=L_const/N1;
tau=T_const/N2;
gamma=tau/h;
%Определение координат узлов сетки
X=x_begin:h:x_end;
T=t_begin:tau:t_end;
N=length(X);
M=length(T);
%Сеточная функция внешней силы f(x,t)
for i=1:N
for j=1:M
f(i,j)=-9*(27/4*X(i)^2-3/2^0.5*T(j)-3)/((9/4*X(i)^2+3/2^0.5*T(j)+1)^3);
end;
end;
%---------------------------------------------------------------------------------------------------
%-------Решение краевой задачи с применением явной разностной схемы--------
%---------------------------------------------------------------------------------------------------
%Сеточная функция U(x,t)
U=zeros(N,M);
%Задание первого начального условия U(x,0)
for i=1:N
U(i,1)=2/((3*X(i)/2)^2+1);
end;
%Задание первого граничного условия U(L,t)
for j=1:M
U(N,j)=8/(13+6*2^0.5*T(j));
end
%Задание второго начального условия Ut(x,0) - по известным U(i,0)
%определяем значения U(i,1) для i=1,...,N-1
for i=2:N-1
U(i,2)=(1-gamma^2)*U(i,1)-4*tau/((9*(X(i)^2)/4+1)^2)+gamma^2*U(i-1,1)/2+gamma^2*U(i+1,1)/2+tau^2*f(i,1)/2;
end
%Определение значения U(0,1) из начальных и граничных условий
U(1,2)=gamma^2*U(2,1)-(gamma^2-1)*U(1,1)-4*tau+tau^2*f(1,1)/2;
%Вычисление значения функции в узлах
for j=2:M-1
%Из второго граничного условия находим U(0,j) для j=2,...,M
U(1,j+1)=2*gamma^2*U(2,j)+2*(1-gamma^2)*U(1,j)-U(1,j-1)+tau^2*f(1,j);
%Находим значения сеточной функции во внутренних узлах сетки
for i=2:N-1
U(i,j+1)=2*(1-gamma^2)*U(i,j)+gamma^2*(U(i-1,j)+U(i+1,j))-U(i,j-1)+tau^2*f(i,j);
end
end
%----------------------------------------------------------------------------------------------------
%------Решение краевой задачи с применением неявной разностной схемы-------
%----------------------------------------------------------------------------------------------------
%Сеточная функция U(x,t)
U_n=zeros(N,M);
%Задание первого начального условия U(x,0)
for i=1:N
U_n(i,1)=2/((3*X(i)/2)^2+1);
end;
%Задание первого граничного условия U(L,t)
for j=1:M
U_n(N,j)=8/(13+6*2^0.5*T(j));
end
%Вычисление значений сеточной функции U(i,1) методом прогонки
%Определение прогоночных коэффициентов
A=zeros(N-1,1);
B=zeros(N-1,1);
ALPHA=zeros(N-1,1);
F=zeros(N,1);
C=zeros(N,1);
BETA=zeros(N,1);
for i=1:N-2
A(i)=gamma^2/2;
B(i+1)=gamma^2/2;
C(i+1)=1+gamma^2;
F(i+1)=U_n(i+1,1)-4*tau/((9*(((i)*h)^2)/4+1)^2)+tau^2*f(i+1,2)/2;
end;
A(N-1)=0;
B(1)=gamma^2;
C(1)=1+gamma^2;
C(N)=1;
F(1)=U_n(1,1)+tau^2*f(1,1)/2-4*tau;
F(N)=8/(13+(6*2^0.5)*tau);
%Прямой ход прогонки
ALPHA(1)=B(1)/C(1);
BETA(1)=F(1)/C(1);
for i=2:N-1
ALPHA(i)=B(i)/(C(i)-A(i-1)*ALPHA(i-1));
BETA(i)=(F(i)+A(i-1)*BETA(i-1))/(C(i)-A(i-1)*ALPHA(i-1));
end;
BETA(N)=(F(N)+A(N-1)*BETA(N-1))/(C(N)-A(N-1)*ALPHA(N-1));
%Обратный ход прогонки
U_n(N,2)=BETA(N);
for i=N-1:-1:1
U_n(i,2)=ALPHA(i)*U_n(i+1,2)+BETA(i);
end;
%Вычисление значений сеточной функции U(i,j) j=2,...,M методом прогонки
%Определение прогоночных коэффициентов
A=zeros(N-1,1);
B=zeros(N-1,1);
ALPHA=zeros(N-1,1);
F=zeros(N,1);
C=zeros(N,1);
BETA=zeros(N,1);
for i=1:N-2
A(i)=gamma^2;
B(i+1)=gamma^2;
C(i+1)=1+2*gamma^2;
end;
A(N-1)=0;
B(1)=2*gamma^2;
C(1)=1+2*gamma^2;
C(N)=1;
for j=3:M
F=zeros(N,1);
F(1)=2*U(1,j-1)-U(1,j-2)+tau^2*f(1,j-1);
F(N)=8/(13+(6*2^0.5)*tau*(j-1));
ALPHA=zeros(N-1,1);
BETA=zeros(N,1);
%Прямой ход прогонки
ALPHA(1)=B(1)/C(1);
BETA(1)=F(1)/C(1);
for i=2:N-1
F(i)=2*U(i,j-1)-U(i,j-2)+tau^2*f(i,j-1);
ALPHA(i)=B(i)/(C(i)-A(i-1)*ALPHA(i-1));
BETA(i)=(F(i)+A(i-1)*BETA(i-1))/(C(i)-A(i-1)*ALPHA(i-1));
end;
BETA(N)=(F(N)+A(N-1)*BETA(N-1))/(C(N)-A(N-1)*ALPHA(N-1));
%Обратный ход прогонки
U_n(N,j)=BETA(N);
for i=N-1:-1:1
U_n(i,j)=ALPHA(i)*U_n(i+1,j)+BETA(i);
end;
end;
Model_graph.m
%Параметры N1, N2 - количество узлов по осям x и t function [U,U_n] = fun(N1,N2) %Задание границ области дискретного изменения аргументаModel.m
%Параметры N1, N2 - количество узлов по осям x и t function [U_a,U,U_n] = fun(N1,N2) %Задание границ области дискретного изменения аргументаMain.m
clear;
clc;
%--------------------------------------------------------------------------
disp('РЕШЕНИЕ УРАВНЕНИЯ КОЛЕБАНИЙ');
disp('Решения, полученные с использованием явной и неявной схем при 50 узлах на пространственной и временной осях');
fun_graph(50,50);
[U1,U2]=fun(10,10);
disp('Таблица значений численного решения уравнения по явной схеме при 10 узлах на пространственной и временной осях');
U1
disp('Таблица значений численного решения уравнения по неявной схеме при 10 узлах на пространственной и временной осях');
U2
%--------------------------------------------------------------------------
L_const=1;
disp('ИССЛЕДОВАНИЕ СХОДИМОСТИ РЕШЕНИЯ С ИСПОЛЬЗОВАНИЕМ ЯВНОЙ И НЕЯВНОЙ СХЕМ');
%Формируем вектор количества узлов по пространственной координате
Point_X=[10 20 50 100 200 500 1000];
T=1000;
%Для определения сходимости метода рассматриваем вложенные сетки
%Таблицы значений функции на самой крупной сетке
[Evident,NotEvident]=fun(Point_X(1),T);
[heigth width]=size(Evident);
last=length(Point_X);
for i=2:last
E=zeros(heigth,width);
NE=zeros(heigth,width);
mult=Point_X(i)/Point_X(1);
[Ev,NEv]=fun(Point_X(i),T);
[row column]=size(Ev);
E(1,1)=Ev(1,1);
E(1,width)=Ev(1,column);
E(heigth,1)=Ev(row,1);
E(heigth,width)=Ev(row,column);
NE(1,1)=NEv(1,1);
NE(1,width)=NEv(1,column);
NE(heigth,1)=NEv(row,1);
NE(heigth,width)=NEv(row,column);
for k=1:row
for l=1:column
if (k==1)
E(k,l)=Ev(k,l);
NE(k,l)=NEv(k,l);
end;
if (mod(k-1,mult)==0)
E((k-1)/mult+1,l)=Ev(k,l);
NE((k-1)/mult+1,l)=NEv(k,l);
end;
end;
end;
disp(strcat('Максимальное расхождение значений сеточной функции при увеличении количества узлов от',32,num2str(Point_X(i-1)),32,'до',32,num2str(Point_X(i))));
disp('Явная схема');
delta_ev=max(max(abs(Evident-E)))
disp('Неявная схема');
delta_nev=max(max(abs(NotEvident-NE)))
disp(strcat('Относительное расхождение значений сеточной функции при увеличении количества узлов от',32,num2str(Point_X(i-1)),32,'до',32,num2str(Point_X(i))));
disp('Явная схема');
%Строка, в которой находится элемент максимального расхождения
[temp index_i_ev]=max(abs(Evident-E));
%Столбец, в котором находится элемент максимального расхождения
[temp index_j_ev]=max(max(abs(Evident-E)));
d_ev=delta_ev/E(index_i_ev(index_j_ev),index_j_ev)
disp('Неявная схема');
%Строка, в которой находится элемент максимального расхождения
[temp index_i_nev]=max(abs(NotEvident-NE));
%Столбец, в котором находится элемент максимального расхождения
[temp index_j_nev]=max(max(abs(NotEvident-NE)));
d_nev=delta_nev/NE(index_i_nev(index_j_nev),index_j_nev)
Evident=E;
NotEvident=NE;
end;
%--------------------------------------------------------------------------
disp('РЕШЕНИЕ МОДЕЛЬНОЙ ЗАДАЧИ');
disp('Решения, полученные с использованием явной и неявной схем при 50 узлах на пространственной и временной осях');
model_graph(50,50);
%--------------------------------------------------------------------------
disp('ПРОВЕРКА СКОРОСТИ СХОДИМОСТИ РАЗНОСТНЫХ СХЕМ');
Point_X=[10 100 1000];
Point_T=[10 100 1000];
last=length(Point_X);
for i=1:last
[M_a,M,M_n]=model(Point_X(i),Point_X(i));
disp(strcat('Норма разности теоретического решения и решения по явной схеме при шаге h=',32,num2str(L_const/Point_X(i))));
d=max(max(abs(M_a-M)))
disp(strcat('Норма разности теоретического решения и решения по неявной схеме при шаге h=',32,num2str(L_const/Point_X(i))));
d_n=max(max(abs(M_a-M_n)))
end;
Список использованной литературы.
1. А.А.Самарский. Теория разностных схем. М. Наука 1983
2. В.Г. Долголаптев, В.Н. Земсков. Численные методы решения разностных уравнений математической физики. Методические указания к курсовой работе по высшей математике.- М., МИЭТ, 1987.
3. Земсков В.Н., Хахалин С.Я. Метод Сеток. Методические указания к выполнению курсовой работы на персональном компьютере. – М., МИЭТ, 1998.
– Конец работы –
Используемые теги: Численные, Методы, решения, краевых, задач, уравнений, математической, физики0.101
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Численные методы решения краевых задач для уравнений математической физики.
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов