ТЕМА АЛГЕБРА ВЫСКАЗЫВАНИЙ. ОСНОВНЫЕ ОПЕРАЦИИ АЛГЕБРЫ ВЫСКАЗЫВАНИЙ

ТЕМА «АЛГЕБРА ВЫСКАЗЫВАНИЙ. ОСНОВНЫЕ ОПЕРАЦИИ АЛГЕБРЫ ВЫСКАЗЫВАНИЙ»

1.Что такое логика? Формальная логика. Математическая логика.

LOGOS (греч.) - слово, понятие, рассуждение, разум.

Слово «логика» обозначает совокупность правил, которым подчиняется процесс мышления.

Основными формами абстрактного мышления являются: понятия, суждения, умозаключения.

Понятие - форма мышления, в которой отражаются существенные признаки отдельного предмета или класса однородных предметов (трапеция, дом).

Суждение - мысль, в которой что-либо утверждается или отрицается о предметах (весна наступила, и грачи прилетели).

Умозаключение - прием мышления, посредством которого из исходного знания получается новое знание (все металлы - простые вещества).

Логика (формальная) - наука о законах и формах правильного мышления.

Математическая логика - изучает логические связи и отношения, лежащие в основе логического (дедуктивного) вывода.

Этапы развития логики.

Написал книги «Категории», «Первая аналитика», «Вторая аналитика». Аристотель создавал логику как науку о доказательстве истины, стремился… Например:

Применение математической логики.

2) В гуманитарных науках (логика, криминалистика). 3) Математическая логика является средством для изучения деятельности мозга -… 4) Идеи и аппарат логики используется в кибернетике, ВТ и электротехнике (построены компьютеры на основе законов…

Алгебра высказываний. Простые и сложные высказывания.

Высказывание - это повествовательное предложение, о котором можно сказать, что оно истинно или ложно. Высказываниями не являются: 1) восклицательные и вопросительные предложения.

Основные операции алгебры высказываний.

Инверсия (логическое отрицание) - присоединение частицы «не» к сказуемому данного простого высказывания или присоединение слов «неверно что. . .» ко всему высказыванию.

Инверсия логической переменной истинна, если сама переменная ложна, и, наоборот, инверсия ложна, если переменная истинна.

Таблица истинности инверсии имеет вид:

А	˥ А

Закон двойного отрицания˥ ˥ А=А.

Пример: Луна — спутник Земли (А). Луна — не спутник Земли ( A)

Дизъюнкция (логическое сложение)- соединение двух простых высказываний A и B в одно составное с помощью союза «или», употребляемого в неисключающем смысле, называется логическим сложением или дизъюнкцией, а полученное составное высказывание — логической суммой.

Указание о необходимости выполнить логическое сложение высказываний A и B записывается так: А+В или А٧В.

А	В	А+В
"шесть-число кратное трем"	"19>37"	"шесть-число кратное трем или 19>37"

Дизъюнкция двух логических переменных ложна тогда и только тогда, когда оба высказывания ложны.

Следующие логические законы можно назвать свойствами дизъюнкции. 1. Закон противоречия. 2. Закон равносильности (идемпотентности idem – лат. тот же самый; potens – лат. сильный) А+А=А

Конъюнкция двух логических переменных истинна тогда и только тогда, когда оба высказывания истинны.

Следующие логические законы можно назвать свойствами конъюнкции. 1. Закон противоречия. 2. Закон равносильности (идемпотентности, idem – лат. тот же самый; potens – лат. сильный)

Свойства импликации.

2. А→0 = 5. 1 →А = А 3. А→А = 1 Эквиваленция.(aequivalens – фр. равноценное) или равнозначность, соответствует оборотам речи «тогда и только тогда» и…

Представление эквиваленции через конъюнкцию, дизъюнкцию и инверсию

А↔В = А· В +·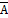

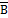
Свойства эквивалентности.

2. А↔ = 0 4. 1 ↔А = А Порядок выполнения логических операций задается круглыми скобками. Но для…

I. Устная работа.

1. Какие предложения являются высказываниями? а) 3+2=5; б) Не шуметь!

I. Актуализация опорных знаний.

1. Что изучает формальная логика?

2. Что изучает математическая логика?

3. Изложите основные этапы развития логики.

4. Области применения математической логики.

5. Что такое высказывание?

6. Какие высказывания бывают?

7. Какие высказывания называются простыми, а какие - сложными?

8. Что не является высказыванием?

9. Основные логические операции и их свойства.

II. Новый материал.

Таблица истинности - это таблица, устанавливающая соответствие между всеми возможными наборами логических переменных, входящих в логическую функцию и значениями функции.

Таблицы истинности применяются для:

- вычисления истинности сложных высказываний;

- установления эквивалентности высказываний;

- определения тождественно-истинных (тавтологий) и тождественно-ложных высказываний.

Установление истинности сложных высказываний.

В состав сложного высказывания входят 3 простых высказывания: А, В, С. В таблице заполняются колонки значениями (0, 1). Указываются все возможные… При составлении таблицы надо следить за тем, чтобы не перепутать порядок… Из таблицы видно, что данное высказывание истинно только в случае, когда А=0, В=1, С=1. Во всех остальных случаях оно…

Эквивалентность высказываний.

ОПРЕДЕЛЕНИЕ.Высказывания называются эквивалентными, если соответствующие значения каждого из них совпадают в таблице истинности. ОПРЕДЕЛЕНИЕ.Если значения сложных высказываний совпадают на всех наборах… Пример 4. Утверждается, что высказывание А+В· С эквивалентно высказыванию (А+В)· (А+С)

Тавтология.

  А А×   Рассмотрим высказывание В+. В этом случае высказывание В+всегда истинно, независимо от истинности В. …

I. Актуализация опорных знаний.

А) Беседа.

3. Расскажите технологию построения таблиц истинности. 4. Что такое эквивалентность? 5. Чем отличается эквиваленция от… 6. Что такое тавтология?

II. Составление таблиц истинности.

Вывод. Высказывание X не эквивалентно высказыванию Y. Упражнение 2. Установить является ли данное высказывание тавтологией. … Вывод. Высказывание является тавтологией.

III. Изучение нового материала.

А) X Y XÙY …   Б) X Y XÚY …

Законы логики.

Перечислим наиболее важные из них: 1. XºX Закон тождества. 2. Закон противоречия

Упрощение формул.

Пример 1. Упростить формулу (А+В)·(А+С)

Решение.

б) По закону идемпотентности A·AºA, следовательно, A×A+A×C+B·A+B·CºA+A×C+B·A+B·C в) В высказываниях А и А·C вынесем за скобки А и используя свойство… г) Аналогично пункту в) вынесем за скобки высказывание А.

Замена эквиваленции и импликации на конъюнкцию, дизъюнкцию и отрицание.

Имеют место следующие равносильности: C®UºÚU (1) C®Uº (2) Докажем равносильность (1) с помощью таблицы истинности: X Y X®U ÚU …

Эквиваленция выражается через конъюнкцию и импликацию

Из (3) и (1) получаем C«Uº(ÚU)×(ÚC)º×Ú Y×Ú… Эта равносильность выражает эквиваленцию через конъюнкцию, дизъюнкцию и отрицание. Из равносильностей (3) и (2)…

Домашнее задание.

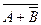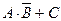1. Формулы данных высказываний преобразовать в эквивалентные, исключив логическое сложение: а) ; б); в) .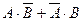

2. Формулы данных высказываний преобразовать в эквивалентные, исключить логическое умножение. а) 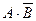; б) ; в) .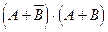

3. Упростить: а) 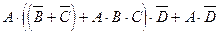; б) ;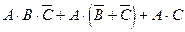

Тема "Множества. Операции над множествами"

СОДЕРЖАНИЕ
1. Способы задания множества
2. Включение и равенство множеств
3. Диаграммы Эйлера-Венна
4. Операции над множествами
а) Объединение множеств; б) Пересечение множеств; в) Разность множеств
г) Дополнение множества

Понятие множества принадлежит к числу основных, неопределяемых понятий математики. Оно не сводится к другим, более простым понятиям. Поэтому его нельзя определить, а можно лишь пояснить, указывая синонимы слова «множество» и приводя примеры множеств: множество – набор, совокупность, собрание каких-либо объектов (элементов), обладающих общим для всех их характеристическим свойством.
Примеры множеств:
1) множество студентов в данной аудитории;
2) множество людей, живущих на нашей планете в данный момент времени;
3) множество точек данной геометрической фигуры;
4) множество чётных чисел;
5) множество корней уравнения х²-5х+6=0;
6) множество действительных корней уравнения х²+9=0;
Основоположник теории множеств немецкий математик Георг Кантор (1845-1918) писал: «Множество есть многое, мыслимое нами как единое». И хотя это высказывание учёного не является в полном смысле логическим определением понятия множества, но оно верно поясняет, что когда говорят о множестве, то имеют в виду некоторое собрание объектов, причём само это собрание рассматривается как единое целое, как один (новый) объект.
Объекты, составляющие данное множество, называют его элементами.
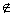Множество обычно обозначают большими латинскими буквами, а элементы множества − малыми латинскими буквам. Если элемент, а принадлежит множеству А, то пишут: а А, а если а не принадлежит А, то пишут: а А.
Например, пусть N–множество натуральных чисел. Тогда 5 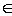N , но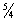 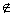N, 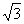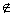N. Если А - множество корней уравнения х²-5х+6=0, то 3 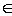А, а 4 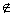А.
В математике часто исследуются так называемые числовые множества, т.е. множества, элементами которых являются числа. Для самых основных числовых множеств утвердились следующие обозначения:
N- множество всех натуральных чисел;
Z- множество всех целых чисел;
Q- множество всех рациональных чисел;
R- множество всех действительных чисел.
Приняты также обозначения Z⁺ , Q⁺, R⁺ соответственно для множеств всех неотрицательных целых, рациональных и действительных чисел, и Z^Ї, Q^Ї, R^Ї -для множеств всех отрицательных целых, рациональных и действительных чисел.
Способы задания множества
Множество А считается заданным, если относительно любого объекта а можно установить, принадлежит этот объект множеству А или не принадлежит; другими словами, если можно определить, является ли а элементом множества А или не является. Существуют два основных способа задания множества:
1) перечисление элементов множества;
2) указание характеристического свойства элементов множества, т.е. такого свойства, которым обладают все элементы данного множества и только они.
Включение и равенство множеств
Пусть Х и У – два множества. Если каждый элемент х множества Х является элементом множества У, то говорят, что множество Х содержится во множестве У и пишут: Х У или У 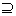Х. Говорят также, что Х включено в У или У включает Х, или что Х является подмножеством множества У. Знаки включения или 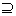относятся только ко множествам и их не следует смешивать со знаками принадлежности Î и . Если, например, А - множество всех студентов вуза, а В – множество студентов-первокурсников этого вуза, то В есть подмножество А, т.е. В А. Пустое множество считают подмножеством любого множества Х, т.е. Ш Х, каким бы ни было множество Х. Ясно также, что каждое множество является подмножеством самого себя: Х Х.
Если для двух множеств Х и У одновременно имеют место два включения Х У и У Х, т.е. Х есть подмножество множества У и У есть подмножество множества Х, то множества Х и У состоят из одних и тех же элементов. Такие множества Х и У называют равными и пишут: Х=У. Например, если А={2; 3}, а В={х | х² –5х+6=0}, то А=В.
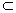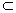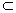Если Х У, но Х≠ У, т.е. существует хотя бы один элемент множества У, не принадлежащий Х, то говорят, что Х есть собственное подмножество множества У, и пишут: Х У. Например: N Z, Z Q, Q 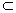R. Далее нам потребуется множество, которое содержит в качестве своего подмножества любое другое множество. Такое «всеобъемлющее» множество будем называть универсальным и обозначать буквой U .
Диаграммы Эйлера-Венна
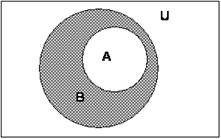
Для наглядного представления множеств используют диаграммы Эйлера-Венна. В этом случае множества обозначают областями на плоскости и внутри этих областей условно располагают элементы множества. Часто все множества на диаграмме размещают внутри прямоугольника, который представляет собой универсальное множество U. Если элемент принадлежит более чем одному множеству, то области, отвечающие таким множествам, должны перекрываться, чтобы общий элемент мог одновременно находиться в соответствующих областях. Выбор формы областей, изображающих множества на диаграммах, может быть произвольным (круги, внутренности эллипсов, многоугольники и т.п.). Покажем, например, с помощью диаграммы Эйлера-Венна, что множество А является подмножеством множества В: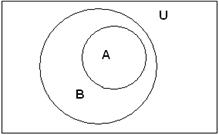
С помощью такой диаграммы становиться наглядным, например, такое утверждение:
если А В, а В С, то А С.

Строгое доказательство этого утверждения, не опирающееся на диаграмму, можно провести так: пусть х А; так как А В, то х В, а так как В С, то из х В следует, что х С; значит, из того, что х А, следует х С, а поэтому А С.
Операции над множествами
С помощью нескольких множеств можно строить новые множества или, как говорят, производить операции над множествами. Мы рассмотрим следующие операции над множествами: объединение, пересечение, разность множеств, дополнение множества. Все рассматриваемые операции над множествами мы будем иллюстрировать на диаграммах Эйлера-Венна.
Объединение множеств
Объединением А В множеств А и В называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из множеств А или В.
Символическая запись этого определения: А В={х | х А или х В}.
Здесь союз «или» понимается в смысле «неразделительного или», т.е. не исключается, что х может принадлежать и А и В. Отметим, что в таком случае элемент х, входящий в оба множества А и В, входит в их объединение только один раз (поскольку для множества не имеет смысла говорить о том, что элемент входит в него несколько раз).
Поясним определение объединения множеств с помощью диаграммы Эйлера-Венна:

На диаграмме объединение множеств А и В выделено штриховкой.
Примеры объединений двух множеств:
1) Пусть А={2; 5; 7}, В={3; 5; 6}. Тогда А В ={2; 3; 5; 6; 7}.
2) Пусть А=[-1/4; 2], В=[ -2/3; 7/4]. Тогда А В=[-2/3; 2] .
3) Пусть А= {х | х=8k, k Z}, B={x | x=8n-4, n Z}. Тогда A B ={x | 4m, m Z}.
Операция объединения множеств может проводиться не только над двумя множествами. Определение объединения множеств можно распространить на случай любого количества множеств и даже – на систему множеств. Система множеств определяется так: если каждому элементу α множества М отвечает множество А_α, то совокупность всех таких множеств мы будем называть системой множеств.
Объединением системы множеств {А_α} называется множество 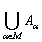, состоящее из всех элементов, принадлежащих хотя бы одному из множеств А_α. При этом общие элементы нескольких множеств не различаются.
Из определения операции объединения непосредственно следует, что она коммутативна, т.е. А₁ A₂ = A₂ А₁, и ассоциативна, т.е. (А₁ A₂) А₃ = А₁ (A₂ А₃).
Пересечение множеств
Пересечением А ∩ В множеств А и В называется множество, состоящее из всех элементов, принадлежащих одновременно каждому из множеств А и В.
Символическая запись этого определения: А ∩ В={х | х А и х В}.
Поясним определение пересечения множеств с помощью диаграммы Эйлера-Венна:

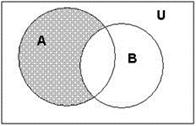
А ∩ В АВ
На диаграмме пересечение множеств А и В выделено штриховкой.
Примеры пересечений двух множеств:
1) Пусть А={2; 5; 7; 8}, В={3; 5; 6; 7} .Тогда А ∩ В={5; 7}.
2) Пусть А=[-1/4; 7/4], В=[-2/3; 3/2]. Тогда А ∩ В= [-1/4; 3/2].
3) Пусть А= {х | х=2k, k є Z}, B={x | x=3n, n є Z}. Тогда А ∩ В ={x | x=6m, m Z}.
Операция пересечения множеств, как и операция объединения, очевидно, коммутативна и ассоциативна, т.е. А₁∩A₂ = A₂ ∩А₁ и (А₁∩A₂)∩ А₃= А₁∩(A₂ ∩ А₃).
Разность множеств
Разностью АВ множеств А и В называется множество, состоящее из всех элементов множества А, которые не принадлежат множеству В, т.е.
АВ={х | х А и х 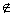В}, что можно пояснить на диаграмме Эйлера-Венна следующим образом:
На диаграмме разность АВ выделена штриховкой.
Примеры разностей множеств:
1. Пусть А={1; 2; 5; 7}, В={1; 3; 5; 6}. Тогда АВ ={2;7}, а ВА={3; 6}.
2. Пусть А=[-1/4;2], В=[-2/3; 7/4]. Тогда АВ=(7/4;2], а ВА=[-2/3; -1/4).
3. Пусть А - множество всех четных целых чисел, В - множество всех целых чисел, делящихся на 3. тогда АВ - множество всех четных целых чисел, которые не делятся на 3, а ВА –множество всех нечетных целых чисел, кратных трем.
Дополнение множества
Пусть множество А и В таковы, что А В. Тогда дополнением множества А до множества В называется разность ВА. В этом случае применяется обозначение С_BА=ВА. Если в качестве множества В берётся универсальное множество U, то применяется обозначение СА=С_UА=UА и такое множество просто называют дополнением множества А. 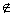Таким образом, символическая запись определения дополнения множества будет следующей: СА={x | x A}.
На диаграммах Эйлера-Венна можно так пояснить определения С_ВА и СА:

 

ТЕМА «УПРОЩЕНИЕ ФОРМУЛ»

1. Формулы данных высказываний преобразовать в эквивалентные, исключив логическое сложение:

а) ;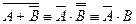

б);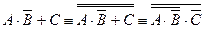

в) .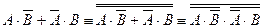

2. Формулы данных высказываний преобразовать в эквивалентные, исключить логическое умножение.

а) ;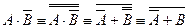

б) ;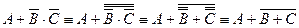

в) .

3. Упростить:

а)

б)

Проверить с помощью таблиц истинности!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!