рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- ОСНОВЫ ВЫСШЕЙ МАТЕМАТИКИ
Реферат Курсовая Конспект
ОСНОВЫ ВЫСШЕЙ МАТЕМАТИКИ
ОСНОВЫ ВЫСШЕЙ МАТЕМАТИКИ - раздел Математика, Министерство Образования Республики Беларусь...
Министерство образования Республики Беларусь
Учреждение образования
Гомельский государственный университет
имени Франциска Скорины»
В.В. БУРАКОВСКИЙ, Т.В. БОРОДИЧ
ОСНОВЫ ВЫСШЕЙ МАТЕМАТИКИ
для студентов исторического факультета,
факультета иностранный язык
Тексты лекций
Гомель 2011 УДК 512 (078) ББК 22.14 Я73Введение
Тексты лекций по учебному курсу ”Основы высшей математики”, предназначенный для обучения студентов факультета иностранных языков, исторического факультета. Тексты лекций написаны в соответствии с действующей программой по данному предмету.
Основное направление текстов лекций – теория вероятностей. В них рассмотрены следующие темы: классическое определение вероятности, основные формулы комбинаторики, геометрические вероятности, теоремы сложения и умножения вероятностей, формулы полной вероятности и Байеса, формула Бернулли, законы распределения и числовые характеристики случайных величин. Содержит основные теоретические сведения, примеры решения задач по теории вероятностей и контрольные задания. Предназначен для студентов математического, физического, экономического и заочного факультетов.
Элементы теории множеств. Множества и операции над ними
Понятие множества является одним из основных математических понятий. Это неопределяемое понятие, его можно только описать или пояснить на примерах. Так, можно говорить о множестве букв в латинском алфавите, множество всех книг в данной библиотеке, множестве студентов в данной группе, множестве всех точек данной линии. Чтобы задать множество, достаточно перечислить элементы или указать характеристические свойства элементов, т.е. такое свойство, которым обладают все элементы данного множества и только они.
Определение 1.1.Предметы (объекты), составляющие некоторое множество, называются его элементами.
Множество принято обозначать прописными латинскими буквами, а элементы множества – строчными буквами. То, что x является элементом множества A, записывается так: x  A (x принадлежит A). Запись вида x
A (x принадлежит A). Запись вида x  A (x
A (x 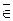 A) означает, что x не принадлежит A, т.е. не является элементом множества A.
A) означает, что x не принадлежит A, т.е. не является элементом множества A.
Элементы множества принято записывать в фигурных скобках. Например, если A – множество, состоящее из первых трех букв латинского алфавита, то его записывают так: A={a,b,c}.
Множество может содержать бесконечно много элементов (множество точек прямой, множество натуральных чисел), конечное число элементов (множество школьников в классе), либо вообще не содержать ни одного элемента (множество студентов пустой аудитории).
 Определение 1.2.Множество, не содержащее ни одного элемента, называется пустым множеством, обозначается Ø.
Определение 1.2.Множество, не содержащее ни одного элемента, называется пустым множеством, обозначается Ø.
Определение 1.3.Множество A называется подмноже-ством множества B, если каждый элемент множества A принадлежит и множеству B. Это обозначается A 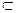 B (A – подмножество B).
B (A – подмножество B).
Пустое множество считают подмножеством любого множества. Если множество A не является подмножеством множества B, то пишут A  B.
B.
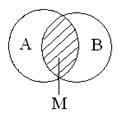 Определение 1.4.Два множества A и B называют равными, если являются подмножествами друг друга. Обозначают A = B. Это означает, что если x
Определение 1.4.Два множества A и B называют равными, если являются подмножествами друг друга. Обозначают A = B. Это означает, что если x  A, то x
A, то x  B и наоборот, т.е. если
B и наоборот, т.е. если 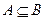 и
и  , то
, то  .
.
Определение 1.5.Пересечение множеств A и B называют множество M, элементы которого являются одновременно элементами обоих множеств A и B. Обозначают M= A 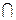 B. Т.е. x
B. Т.е. x  A
A 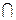 B, то x
B, то x  A и x
A и x  B.
B.
Записывают A 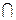 B={ x | x
B={ x | x  A и x
A и x  B }. (Вместо союза и – ставятся знаки
B }. (Вместо союза и – ставятся знаки  , &).
, &).
 Определение 1.6.Если A
Определение 1.6.Если A 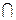 B= Ø, то говорят, что множества A и B не пересекаются.
B= Ø, то говорят, что множества A и B не пересекаются.
Аналогично можно определить пересечение 3-х, 4-х и любого конечного числа множеств.
 Определение 1.7.Объединением множеств A и B называют множество M, элементы которого принадлежат хотя бы одному из данных множеств. Обозначают M=A
Определение 1.7.Объединением множеств A и B называют множество M, элементы которого принадлежат хотя бы одному из данных множеств. Обозначают M=A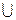 B. Т.о. A
B. Т.о. A 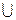 B={ x | x
B={ x | x  A или x
A или x  B }. (Вместо союза или – ставится знак
B }. (Вместо союза или – ставится знак 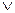 ).
).
Аналогично определяется и множество A1 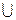 A2
A2 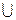 …
… 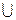 An. Оно состоит из элементов, каждый из которых принадлежит хотя бы одному из множеств A1, A2,…, An (а может быть, и нескольким сразу).
An. Оно состоит из элементов, каждый из которых принадлежит хотя бы одному из множеств A1, A2,…, An (а может быть, и нескольким сразу).
Пример 1.8. 1) если A={1;2;3;4;5} и B={1;3;5;7;9}, то A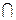 B={1;3;5} и A
B={1;3;5} и A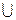 B={1;2;3;4;5;7;9}.
B={1;2;3;4;5;7;9}.
2) если A={2;4} и B={3;7}, то A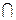 B= Ø и A
B= Ø и A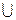 B={2;3;4;7}.
B={2;3;4;7}.
3) если A={летние месяцы} и B={месяцы, в которых 30 дней}, то A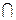 B={июнь} и A
B={июнь} и A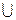 B={апрель; июнь; июль; август; сентябрь; ноябрь}.
B={апрель; июнь; июль; август; сентябрь; ноябрь}.
Определение 1.9.Натуральными называются числа 1,2,3,4,…, используемые для счета предметов.
Множество натуральных чисел обозначается N, N={1;2;3;4;…;n;…}. Оно является бесконечным, имеет наименьший элемент 1 и не имеет наибольшего элемента.
Пример 1.10. A – множество натуральных делителей числа 40. Перечислить элементы этого множества. Верно ли, что 5  A, 10
A, 10  A, -8
A, -8  A, 4
A, 4  A, 0
A, 0 A, 0
A, 0  A.
A.
 A = {1,2,4,5,8,10,20,40}. (В,В,Н,Н,Н,В)
A = {1,2,4,5,8,10,20,40}. (В,В,Н,Н,Н,В)
Пример 1.11.Перечислите элементы множеств, заданных характеристическими свойствами:
а) А={x | (x-1)(2x-1)(3+x)=0}, получаем A = {1; ;-3}
;-3}
б) B={x | -1,1< x < 5  x
x  N}, имеем B = {1;2;3;4}.
N}, имеем B = {1;2;3;4}.
Пример 1.12.Дано множество чисел K = {21;54;153;171;234}. Составить подмножество чисел из K, которые а) делятся на 7; б) делятся на 9; в) не делятся на 5; г) делятся на 4.
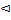 а) A = {21}, б) B = {54;153;171;234}, в) C = K, г) D= Ø
а) A = {21}, б) B = {54;153;171;234}, в) C = K, г) D= Ø 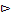
Пример 1.13.Множество C состоит из 11 элементов, множество D – из 8. Сколько элементов содержит C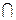 D , если C
D , если C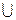 D содержит 15 элементов?
D содержит 15 элементов?
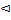 Поскольку A+B –A
Поскольку A+B –A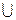 B=A
B=A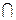 B, тогда 11+8–15=4
B, тогда 11+8–15=4 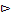
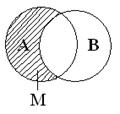 Определение 1.14.Разность множеств A и B называется множество M, элементы которого принадлежат множеству A и не принадлежат множеству B.
Определение 1.14.Разность множеств A и B называется множество M, элементы которого принадлежат множеству A и не принадлежат множеству B.
Обозначают M=A B.
Таким образом, A B={x | x  A и x
A и x  B}.
B}.
Пример 1.15. Если A = {1;2;3;4;5} и B = {1;5}, то AB={2;3;4}.
Функции и способы их задания.
Пусть X и Y некоторые множества.
Определение 2.1.Функцией называется отношение (соответствие) f между множествами X и Y, при котором каждому элементу x  X соответствует единственный элемент y
X соответствует единственный элемент y  Y. Множество X называют областью определения функции и обозначают D(f), а множество {f(x)}
Y. Множество X называют областью определения функции и обозначают D(f), а множество {f(x)} 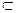 Y – областью или множеством значения функции и обозначают E(f).
Y – областью или множеством значения функции и обозначают E(f).
Определение 2.2.Переменную x  D(f)называют независимой переменной или аргументом, а y
D(f)называют независимой переменной или аргументом, а y  E(f) называют зависимой переменной или функцией.
E(f) называют зависимой переменной или функцией.
Определение 2.3.Если X и Y – числовые множества, то y=f(x) называется числовой функцией.
 Пример 2.4.Пусть даны два множества X={2;3;5;7}, Y={15;18;31}. Установим между ними такое соответствие: элемент x
Пример 2.4.Пусть даны два множества X={2;3;5;7}, Y={15;18;31}. Установим между ними такое соответствие: элемент x X является делителем элемента y
X является делителем элемента y Y. Тогда каждому элементу множества X соответствует только один элемент множества Y: 2
Y. Тогда каждому элементу множества X соответствует только один элемент множества Y: 2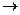 28; 3
28; 3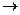 15; 5
15; 5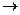 15; 7
15; 7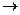 28. Следовательно, задана функция.
28. Следовательно, задана функция.
Существуют три способа задания функции: аналитический, графический и табличный.
Если указана совокупность операций, которые нужно произвести над аргументом x, чтобы получить значение функции, то говорят, что функция задана аналитическим выражением.
Примером могут служить функции y=x2-5x+1, x [0,1], y=x2+7x-1, x
[0,1], y=x2+7x-1, x (
( ;
;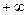 ). Они заданы на различных множествах.
). Они заданы на различных множествах.
Функция может задаваться на различных числовых множествах различными аналитическими выражениями, например
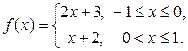
Эта функция определена [-1;1]. Для вычисления значения функции нужно выяснить, каким аналитическим выражением следует воспользоваться для заданного конкретного значения аргумента.
Определение 2.5.Множество из n элементов {a1, a2, …, an}, для каждого из которых установлено, какой является 1-м, 2-м, …, n-м, называется упорядоченной n-кой (a1, a2, …, an).
Определение 2.6.Множество упорядоченных пар действительных чисел, т.е. {(x;y) | x
 , y
, y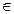
 }, называется числовой плоскостью. Обозначают ее
}, называется числовой плоскостью. Обозначают ее 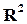 .
.
Способ задания функции с помощью графика на координатной плоскости называется графическим.
При табличном способе задания функции приводится таблица, в которой даются значения функции для конечного множества значений аргумента.
Предмет и задачи теории вероятностей. События и операции над ними. Относительные частоты и их свойства
Возникновение теории вероятностей относят к XVII веку и связывают с решением комбинаторных задач теории азартных игр и потребностями страхового дела. Азартные игры (карты, кости) дали стимул для построения математических моделей игровых ситуаций. Эти модели предоставляли игроку возможность ориентироваться в ходе игры, делать расчеты ставок, оценивать шансы выигрыша, а также позволяли планировать расходы и доходы страховых компаний и т.д.
Разработкой таких моделей занимались в 17 веке Б. Паскаль, П. Ферма, Х. Гюйгенс. Основы классической теории вероятности были сформулированы в 18 веке Я. Бернулли, П. Лапласом, С. Пуассоном, К. Гауссом. В 1933году А.Н. Колмогоров сформулировал аксиомы теории вероятности, базирующиеся на теории множеств.
Однако с теорией вероятностей развивалась и другая современная дисциплина – математическая статистика, которая широко применяется в экономике, технике, социологии, медицине, физике, лингвистическом программировании и др.
Определение 3.1.Предметом теории вероятностей является количественный и качественный анализ математических моделей вероятностных экспериментов, называемый статистической обработкой экспериментальных данных.
Вероятностные эксперименты имеют следующие общие черты: непредвиденность результата; наличие определенных количественных закономерностей при их многократном повторении при одинаковых условиях; множество возможных исходов.
Определение 3.2.Вероятностными называют эксперименты, которые можно повторить произвольное число раз при соблюдении одних и тех же стабильных условий, однако их исходы неоднозначны, случайны.
Определение 3.3.Теория вероятностей – наука, занимающаяся анализом математических моделей для принятия решений в условиях неопределенности.
Первичным понятием теории вероятности, не определенным через другие понятия, является пространство элементарных исходов Ω.
Обычно в качестве пространства элементарных исходов берутся единственно возможные неразложимые результаты эксперимента.
Пример 3.4.Приведем примерыпространств элементарных исходов:
1) При бросании симметричной монеты в качестве Ω выбирается Ω={г,р}.
2) При бросании игральной кости пространство элементарных исходов следующее Ω={1,2,3,4,5,6}.
3) При бросании двух симметричных монет Ω={(р,р),(р,г),(г,р),(г,г)}.
 4) При бросании двух игральных костей Ω={(i,j) | i,j
4) При бросании двух игральных костей Ω={(i,j) | i,j 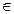 {1,…,6}}, n=36.
{1,…,6}}, n=36.
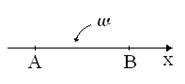
 5) Пусть на [AB] наудачу бросается точка Ω={ω | ω
5) Пусть на [AB] наудачу бросается точка Ω={ω | ω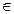 [AB]}=[AB].
[AB]}=[AB].
6) Пусть на [AB] наудачу бросаются две точки
Ω={(x,y) | x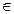 [AB], y
[AB], y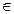 [AB]}=[AB]× [AB].
[AB]}=[AB]× [AB].
Определение 3.5.Опытом или испытанием называют всякое осуществление определённого комплекса условий или действий, при которых происходит соответствующее явление. Возможный результат опыта называют событием, те событием называется произвольное подмножество A пространства элементарных исходов Ω.
Пример 3.6. Опытом является подбрасывание монеты, а событиями “герб”, “цифра на верхней ее стороне” (когда монета упадет). Опытами являются стрельба по мишени, извлечение шара из ящика и т.п. События будем обозначать заглавными буквами латинского алфавита А, В, С.
Определение 3.7.Каждое событие, которое может наступить в итоге опыта, называется элементарным исходом (элементарным событием, или шансом).
Определение 3.8.Элементарные исходы, при которых данное событие наступает, называются благоприятствующими этому событию, или благоприятными шансами, т.е. те элементарные исходы, из которых состоит событие A, называются благоприятствующими событию A.
Пример 3.9.Так, при подбрасывании игрального кубика элементарные исходы А1, А3, А5 являются благоприятствующими событию “выпало нечетно число очков”.
Говорят, что событие A произошло, если в результате эксперимента происходит элементарный исход благоприятствующий событию A, т.е. ω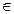 A.
A.
Определение 3.10.Событие называется достоверным, в данном опыте, если оно обязательно произойдет в этом опыте, т.е. все пространство элементарных исходов Ω, если его взять в качестве события, называют достоверным событием, поскольку оно происходит в любом эксперименте (всегда).
Пример 3.11. Если в ящике только голубые шары, то событие “из ящика извлечен голубой шар” является достоверным (в ящике нет шаров другого цвета).
Определение 3.12. Событие называется невозможным, в данном опыте, если оно не может произойти в этом опыте.
Пустое множество Ø (т.е. множество, не содержащее ни одного элементарного исхода) называется невозможным событием, поскольку оно никогда не произойдет.
Пример 3.13. Так, если в ящике находятся только красные шары, то событие “из ящика извечен голубой шар” является невозможным (таких шаров в ящике нет).
Определение 3.14. Событие называется случайным в данном опыте, если око может произойти, а может и не произойти в этом опыте, т.е. все остальные события, кроме достоверного и невозможного, называются случайными.
Пример 3.15. Если в ящике находятся n голубых и m красных шаров, одинаковы по размеру и весу, то событие “из урны извлечен голубой шар” является случайным (оно может произойти, а может и не произойти, поскольку в урне имеются не только голубые, но и красные шары). Случайными событиями являются “герб” и “цифра на верхней стороне монеты при ее подбрасывании”, “попадание и промах при стрельбе по мишени”, “выигрыш по билету лотереи” и т.п.
Замечание 3.16. Приведенные примеры свидетельствуют о том, что одно и то же событие в некотором опыте может быть достоверным, в другом – невозможным, в третьем - случайным. Говоря о достоверности, невозможности, случайности события, имеют в виду его достоверность, невозможность, случайность по отношению к конкретному опыту, т.е. к наличию определенного комплекса условий или действий.
Определение 3.17. Два события называются совместными в данном опыте, если появление одного из них не исключает появление другого в этом опыте.
Пример 3.18.Так, при подбрасывании двух симметричных монет, событие A – «герб на верхней стороне первой монеты” и B – “цифра на верхней стороне второй монеты” являются совместными.
 Операции над событиями.
Операции над событиями.
Определение 3.19. Суммой событий A и B называют объединение этих множеств A 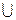 B.
B.
Обозначают A + B={ x | x  A или x
A или x  B }.
B }.
Вместо союза или – ставится знак 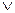 .
.
 Определение 3.20.Произведением событий A и B называют пересечение множеств A
Определение 3.20.Произведением событий A и B называют пересечение множеств A 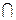 B.
B.
Обозначают AB={ x | x  A и x
A и x  B }.
B }.
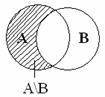 Вместо союза и – ставятся знаки
Вместо союза и – ставятся знаки  , &.
, &.
Определение 3.21.Разностью событий A и B называют разность множеств A B.
Обозначают A B={x | x  A и x
A и x  B}.
B}.
 Определение 3.22.Два события называются несовместными, если они не могут произойти вместе при одном и том же испытании, т.е. события A и B называются несовместимыми (несовместными), если AB = Ø.
Определение 3.22.Два события называются несовместными, если они не могут произойти вместе при одном и том же испытании, т.е. события A и B называются несовместимыми (несовместными), если AB = Ø.
Если AB = Ø, то будем говорить, что A 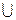 B= A + B.
B= A + B.
Так, несовместными являются попадание и промах при одном выстреле.
 Несколько событий называются несовместными, если они попарно несовместны.
Несколько событий называются несовместными, если они попарно несовместны.
Определение 3.23.Говорят, что событие A влечет событие B, если A 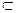 B.
B.
 Определение 3.24. Два события называются противоположными, если появление одного из них равносильно непоявлению другого. Если одно из противоположных событий обозначено буквой A, то другое обозначают Ā. Таким образом событие Ā = Ω A называется противоположным к событию A.
Определение 3.24. Два события называются противоположными, если появление одного из них равносильно непоявлению другого. Если одно из противоположных событий обозначено буквой A, то другое обозначают Ā. Таким образом событие Ā = Ω A называется противоположным к событию A.
Пример 3.25.1)Так, противоположными являются события “герб” и “цифра” при одном подбрасывании симметричной монеты.
2) Если A – “попадание”, то Ā – “промах” при одном выстреле по мишени.
3) При бросании игральной кости Ω={1,2,3,4,5,6}. Если A – выпадение нечетного числа очков, т.е. A={1,3,5,}, то Ā ={2,4,6} – противоположное событие (выпадение четного числа очков).
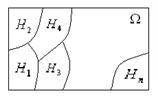 Определение 3.26.Множество событий H1, H2,…, Hn называют полной группой событий, если они попарно-несовместны; появление одного и только одного из них является достоверным событием.
Определение 3.26.Множество событий H1, H2,…, Hn называют полной группой событий, если они попарно-несовместны; появление одного и только одного из них является достоверным событием.
Таким образом события H1, H2,…, Hn образуют полную группу, если H1+ H2+…+ Hn= Ω (т.е. Hi Hj=Ø, если i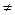 j).
j).
В частности события A и Ā образуют полную группу, т.к. A +Ā= Ω.
Пример 3.27. Рассмотрим события, появляющиеся при подбрасывании игрального кубика (т.е. кубика, на гранях которого записаны цифры 1,2,3,4,5,6 или изображены знаки, соответствующие этим цифрам). Когда кубик упадет, то верхней гранью окажется грань с одной из этих цифр. Событие: “верхней гранью оказалась грань с цифрой k” обозначим через Аk (k=1,2,3,4,5,6). События А1, А2, А3, А4, А5, А6 образуют полную группу: они попарно-несовместны; появление одного и только одного из них является достоверным событием (когда кубик упадет, то только одна из граней окажется верхней, на ней написана только одна цифра от 1 до 6).
Определение 3.28.События считают равновозможными, если нет оснований полагать, что одно событие является более возможным, чем другие.
Пример 3.29. При подбрасывании монеты событие A (появление цифры) и событие B (появление герба) равновозможны, так как предполагается, что монета изготовлена из однородного материала, имеет правильную цилиндрическую форму и наличие чеканки не влияет на то, какая сторона монеты (герб или цифра) окажется верхней. При подбрасывании игрального кубика события А1, А2, А3, А4, А5, А6 являются равновозможными, поскольку предполагается, что кубик изготовлен из однородного материала, имеет правильную форму и наличие цифр (или очков) на гранях не влияет на то, какая из шести граней окажется верхней.
Относительные частоты и их свойства.
Пусть производится некоторый случайный (вероятностный) эксперимент, пространством элементарных исходов является множество Ω. Рассмотрим некоторое событие A (A 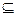 Ω). Если эксперимент произвести N раз, а событие A появится в них N(A) раз, то число W(A)=
Ω). Если эксперимент произвести N раз, а событие A появится в них N(A) раз, то число W(A)= называется относительной частотой появления события A.
называется относительной частотой появления события A.
Свойство 3.30. Относительная частота произвольного события неотрицательна, т.е. 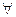 A
A 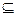 Ω, W(A)
Ω, W(A)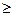 0.
0.
Свойство 3.31.Относительная частота достоверного события равна 1.
W(A)= =
=  =1.
=1.
Свойство 3.32. (аддитивности). Относительная частота суммы несовместных событий равна сумме относительных частот этих событий.
W(A+B)=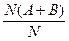 =
= 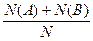 =
= +
+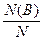 = W(A)+ W(B).
= W(A)+ W(B).
Аксиомы теории вероятностей. Дискретные пространства элементарных исходов. Классическое определение вероятности
Пусть Ω пространство элементарных исходов, F – множество всех подмножеств Ω. Любому событию A  F ставится в соответствие действительное число P(A), называемое вероятностью события A, при этом выполняются аксиомы теории вероятности:
F ставится в соответствие действительное число P(A), называемое вероятностью события A, при этом выполняются аксиомы теории вероятности:
Аксиома 4.1. Вероятность произвольного события неотрицательна, т.е. 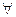 A
A  F, P(A)
F, P(A)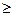 0.
0.
Аксиома 4.2. Вероятность достоверного события равна 1, т.е. P(Ω)=1.
Аксиома 4.3. (счетной аддитивности) Если A1, A2,…  F и Ai∙ Aj=Ø (i
F и Ai∙ Aj=Ø (i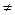 j), то P(A1+ A2+…) = P(A1)+P( A2)+… или P(
j), то P(A1+ A2+…) = P(A1)+P( A2)+… или P(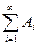 ) =
) =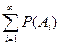 .
.
Определение 4.4.Бесконечное множество называется счетным, если элементы этого множества можно занумеровать натуральными числами.
Все другие множества называются несчетными (например, множество точек [a,b] ненулевой длины).
Определение 4.5. Пространство элементарных исходов называется дискретным, если оно конечное или счетное, т.е. Ω={ω1, … , ωn} или Ω={ω1, ω2,… }.
Любому элементарному исходу ωi ставится в соответствие число p(ωi), так что при этом  =1.
=1.
Определение 4.6. Вероятностью события A называется число P(A)= .
.
Пример 4.7. Бросается игральная кость. Найти вероятность выпадения нечетного числа очков.
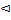 p(ωi)=
p(ωi)=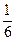 , i =1,..,6,
, i =1,..,6,  P(A)= p(ω1, ω3, ω5)=
P(A)= p(ω1, ω3, ω5)= 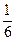 +
+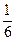 +
+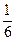 =
= 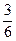 =
=  .
. 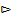
Сформулируем следующие предположения:
1. Пространство элементарных исходов конечно: Ω={ω1, … , ωn}.
2. Все элементарные исходы равновероятны (равновозможны), т.е. p(ω1)= p(ω2)=…= p(ωn).
Поскольку 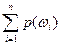 =1, то p(ωi)=
=1, то p(ωi)= , i =1,..,n.
, i =1,..,n.
Рассмотрим некоторое событие A 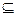 Ω, состоящее из k элементарных исходов, k
Ω, состоящее из k элементарных исходов, k 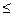 n, A={
n, A={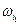 ,
, 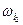 ,…,
,…,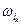 }.
}.
Вероятность события P(A)=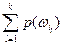 =
= 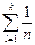 =
=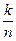 .
.
Определение 4.8. (классическое определение вероятности) Если пространство элементарных исходов конечно, а все элементарные исходы равновероятны, то вероятность события A называется отношение числа элементарных исходов, благоприятствующих A, к общему числу всех возможных элементарных исходов P(A)=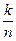 .
.
Пример 4.9.Бросается две монеты. Найти вероятность того, что хотя бы на одной выпадет герб.
 Ω={(г,г), (г,р), (р,г), (р,р)}, n=4.
Ω={(г,г), (г,р), (р,г), (р,р)}, n=4.
A={(г,г), (г,р), (р,г)}, k=3.
Таким образом, P(A)=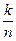 =
= 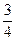 .
. 
Пример 4.10. Бросаются две игральные кости. Какова вероятность того, что сумма выпавших очков равна 7?
 Ω={(i,j) | i,j
Ω={(i,j) | i,j  {1,..,6}}, n=36,
{1,..,6}}, n=36,
A={ (6,1), (5,2), (4,3), (3,5), (2,5), (1,6)}, k=6,
Таким образом, P(A)=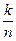 =
=  =
=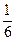 .
. 
Основные правила комбинаторики. Выборки, сочетания. Аксиомы теории вероятностей
Лемма 5.1. Из m элементов a1,…,an первой группы и n элементов b1,…,bn второй группы можно составить ровно m∙n упорядоченных пар вида (ai, bj),… (a1, b1), (a1, b2), …, (a1, bn), Всегоm∙n парГеометрические вероятности
Пусть на числовой оси имеется отрезок [a,b] и на него наудачу бросается точка. Вероятность того, что эта точка попадёт на [c,d][a,b], вычисляется по… Р{ω[c,d]}= – геометрическая вероятность на прямой.Свойства вероятности
Свойство 7.2. Вероятность достоверного события равна 1: Р(Ω)=1. Свойство 7.3. Для любого события А верно, что 0Р(А)1. Р(А)=. Т.к. 0n, то 01, следовательно 0Р(А)1.Условная вероятность. Независимость
Определение 8.1.Условной вероятностью события В при условии А называется вероятность события В в предположении, что событие А наступило. Обозначение: Р(В|A) = PA(B). Находится по формуле: Р(В|A)=(1). Теорема 8.2. (умножение вероятностей)Формулы полной вероятности и Байеса
Теорема 9.1. (формула полной вероятности) Если события H1, H2,…, Hn образуют полную группу, то вероятность появления события А, которое может… Р(А)=Р(H1)P(A|H1) + … + Р(Hn)P(A|Hn) или Р(А)= . Поскольку события образуют полную группу, то Ω= H1+H2+…+Hn. Событие А происходит только с одним из событий Hi,…Схема независимых испытаний Бернулли. Полиноминальное распределение
Предположим, что производятся независимо друг от друга nиспытаний, в каждом из которых возможны только 2 исхода: успех и неудача («У»,»Н»). Причём вероятность успеха Р(У)=p, Р(Н)=q , p+q=1.
Определение 10.1. Последовательность  испытаний называется испытаниями Бернулли, если эти испытания независимы, в каждом из них возможны 2 исхода, причём вероятности этих исходов не меняются от испытания к испытанию.
испытаний называется испытаниями Бернулли, если эти испытания независимы, в каждом из них возможны 2 исхода, причём вероятности этих исходов не меняются от испытания к испытанию.
В nиспытаниях Бернулли элементарным исходом является:
(ω1, ω2,…, ωn), где ωi {У,Н}, i
{У,Н}, i {1,…,n}.
{1,…,n}.
Всего таких исходов 2n. Поскольку испытания независимы, то:
Р(ω1, ω2,…, ωn)= Р(ω1)P(ω2)…P(ωn).
Обозначим через Pn(k) вероятность того, что в n испытаниях Бернулли произошло ровно k успехов. Тогда
Pn(k)=Р{(У,…,У,Н,…,Н),(У,…,У,Н,У,Н,…,Н),…,(Н,…,Н,У,…У)}=
= pkqn-k + pkqn-k + …+ pkqn-k =  pkqn-k.
pkqn-k.
Таким образом получим
Pn(k)=  pkqn-k, k
pkqn-k, k {0,…,n} , p+q=1 – формула Бернулли.
{0,…,n} , p+q=1 – формула Бернулли.
Пример 10.2. Двое равных по силам шахматистов играют в шахматы. Что вероятнее: выиграть одну партию из двух или две из четырёх? Ничьи во внимание не принимаются.
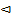 p=q=
p=q= , P2(1)=
, P2(1)= ∙
∙ ∙
∙ =
= =
= ;
;
P4(2)= ∙(
∙( )2∙(
)2∙( )2=6∙
)2=6∙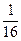 =
= ;
;
Таким образом P2(1)> P4(2).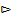
Полиноминальное распределение
Предположим, что производится независимо друг от друга n испытаний, в каждом из которых возможны k исходов E1, E2,…, Ek. Вероятность этих исходов обозначим P(Ei)=pi, i {1,…,k}. Причём
{1,…,k}. Причём  =1, k>2.Вероятность того, что в n испытаниях исход E1 появится r1 раз, E2
=1, k>2.Вероятность того, что в n испытаниях исход E1 появится r1 раз, E2 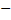 r2 раз, …, E1 – rk раз, где
r2 раз, …, E1 – rk раз, где  =n, находится по формуле:
=n, находится по формуле:
P(r1, r2,…, rk)=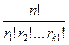
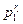
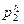 …
… ,
,  =1,
=1,  =n – формула полиноминального распределения.
=n – формула полиноминального распределения.
Замечание 10.3. Формула полиноминального распределения обобщает формулу Бернулли на случай более 2 исходов в каждом испытании.
Пример 10.4.В урне 3 шара: белый, красный, синий. Из урны 5 раз наудачу извлекаются шары с возвращением. Найти вероятность того, что белый шар извлечён 3 раза, а красный и синий –по одному разу.
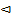 Поскольку p1= p2= p3=
Поскольку p1= p2= p3=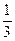 ; r1 =3, r2=1, r3 =1.
; r1 =3, r2=1, r3 =1.
Тогда P5(3,1,1)= ∙(
∙(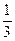 )3∙
)3∙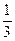 ∙
∙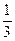 = 20∙
= 20∙ =
= 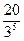 =
= .
. 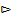
Теорема Пуассона. Локальная и интегральная теоремы Муавра-Лапласа
Теорема 11.1. (Пуассона) Пусть производится n независимых испытаний, в каждом из которых событие А наступает с вероятностью р. Тогда, если число… По формуле Бернулли вероятность того, что событие появится ровно k раз в n… Pn(k)= pkqn-k=pk(1 - p)n-k.Случайные величины
Определение 12.1. Случайной величиной Х называется функция Х(ω), отображающая пространство элементарных исходов Ω во множество… Пример 12.2. Дважды подбрасывается монета. Рассмотрим случайную величину Х –…Дискретные случайные величины
Определение 13.2. Законом распределения случайной величины Х называется совокупность пар чисел (,), где – возможные значения случайной величины, а –… Простейшей формой задания дискретной случайной величины является таблица, в…Лекция 15 Непрерывные случайные величины
Определение 15.1.Говорят, что случайная величина Х имеет вероятность или плотность распределения вероятностей, если существует функция p(x)такая,… =P{X<x}=(1). Пример 15.2. Функция распределения случайной величины Х имеет видВысшая математика
Тексты лекций
Рекомендованы к изданию научно-методическим советом учреждения образования…– Конец работы –
Используемые теги: основы, высшей, математики0.062
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: ОСНОВЫ ВЫСШЕЙ МАТЕМАТИКИ
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов