рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Математической статистике
Реферат Курсовая Конспект
Математической статистике
Математической статистике - раздел Математика, Государственное Образовательное Учреждение Высшего Професс...
Государственное образовательное учреждение
высшего профессионального образования
«Пермская государственная медицинская академия
имени академика Е.А. Вагнера
Федерального агентства по здравоохранению и социальному развитию»
Учебно-методическое пособие
к практическим занятиям
по высшей математике
и
математической статистике
ПЕРМЬ 2009
Авторы-составители:
Кирко Г.Е.- д-р физ.-мат. наук, проф., Кустова Я.Р., Афанасьев А.Л., Корякина А.Г., Смирнова З.А., Зернина Н.В., Сазонова Н.К., Черемных М.Р.
УДК 510 (022)+519.24/.27(075.8)
ББК 22.11+22.172 я73
М.54
УЧЕБНО-МЕТОДИЧЕСКОЕ ПОСОБИЕ к практическим занятиям по высшей математике и математической статистике: учебное пособие для студентов первого курса медицинских вузов/ Г.Е. Кирко и др./ Пермь: ГОУ ВПО ПГМА им. ак. Е.А. Вагнера Росздрава, 2009.-97 с.
ISBN 978-5-7812-0405-6
В составе методического пособия около 400 задач по высшей математике в соответствии с учебной программой.
В начале каждой главы приведены основные формулы и уравнения и даны примеры решения типовых задач, в которых отражены вопросы методики решения задач по данному разделу курса высшей математики. Некоторые задачи содержат материал, связанный с практическим использованием аппарата высшей математики в биологии и медицине. Пособие предназначено для студентов первого курса лечебного, педиатрического, стоматологического и медико-профилактического факультетов медицинских вузов.
ISBN 978-5-7812-0405-6
Рецензенты:
кафедра физики Пермского государственного университета, зав. кафедрой, д-р физ.-мат. наук, профессор Г.Ф. Путин.
М.И. Вахрин - канд. физ.-мат. наук, доцент, зав. кафедрой физики и математики Пермской государственной фармацевтической академии.
Печатается по решению ученого совета ГОУ ВПО ПГМА им. ак. Е.А. Вагнера Росздрава.
УДК 510 (022)+519.24/.27(075.8)
ББК 22.11+22.172 я73
ISBN 978-5-7812-0405-6 ©ГОУ ВПО ПГМА им. ак. Е.А. Вагнера Росздрава, 2009
© Коллектив авторов, 2009
СОДЕРЖАНИЕ
| Глава I. | Пределы…………………………………………………….. | |||
| Глава 2. | Дифференциальное исчисление функций одной независимой переменной………………………………….. | |||
| §1. | Понятие производной……………………………….. | |||
| §2. | Основные правила дифференцирования. Дифференцирование основных элементарных функций………………………………………………. | |||
| §3. | Дифференцирование сложной функции…………… | |||
| §4. | Производные высших порядков……………………. | |||
| §5. | Дифференциал функции…………………………….. | |||
| §6. | Применение производной при решении прикладных задач……………………………………. | |||
| Глава 3. | Исследование функций методами дифференциального исчисления…………………………………………………. | |||
| §1. | Интервалы монотонности функции……………….. | |||
| §2. | Экстремум функции………………………………… | |||
| Глава 4. | Неопределенный интеграл………………………………... | |||
| §1. | Непосредственное интегрирование………………… | |||
| §2. | Интегрирование способом подстановки (методом замены переменной)……………………... | |||
| §3. | Интегрирование по частям………………………….. | |||
| §4. | Применение неопределенного интеграла при решении прикладных задач…………………………. | |||
| Глава 5. | Определенный интеграл…………………………………... | |||
| §1. | Определенный интеграл и его непосредственное интегрирование……………………………………… | |||
| §2. | Приложение определенного интеграла для вычисления площадей плоских фигур……………... | |||
| §3. | Приложение определенного интеграла к решению физических задач……………………………………. | |||
| Глава 6. | Дифференциальные уравнения…………………………… | |||
| §1. | Основные понятия…………………………………… | |||
| §2. | Уравнения с разделяющимися переменными……... | |||
| §3. | Однородные дифференциальные уравнения………. | |||
| §4. | Задачи на составление дифференциальных уравнений…………………………………………… | |||
| Глава 7. | Элементы теории вероятностей и математической статистики………………………………………………….. | |||
| §1. | Основные понятия…………………………………… | |||
| §2. | Числовые характеристики распределения случайных величин………………………………….. | |||
| §3. | Нормальный закон распределения случайных величин……………………………………………….. | |||
| §4. | Генеральная совокупность. Оценка параметров генеральной совокупности по ее выборке…………. | |||
| §5. | Интервальная оценка. Интервальная оценка при малой выборке. Распределение Стьюдента……….. | |||
| §6. | Проверка гипотез. Критерии значимости………….. | |||
| §7. | Элементы корреляционного и регрессионного анализа………………………………………………... | |||
| 7.1. Характер взаимосвязи между признаками……. | ||||
| 7.2. Проведение корреляционного анализа с помощью коэффициента парной корреляции….. | ||||
| 7.3. Элементы регрессионного анализа…………….. | ||||
| Лабораторные работы по статистической обработке результатов……………………………………………………………. | ||||
| 1. | Статистическая обработка данных измерения роста…………………………………………………... | |||
| 2. | Задания для проведения статистического анализа совокупности данных……………………………….. | |||
| Приложение…………………………………………………………… | ||||
| П1. | Правила приближенных вычислений………………. | |||
| П1.1 | Запись приближенных чисел……………………….. | |||
| П1.2 | Правила округления…………………………………. | |||
| П1.3 | Вычисление с приближенными числами…………... | |||
| Ответы……..………………………………………………………… | ||||
| Список литературы…………………………………………………... | ||||
Никакой достоверности нет в науках там, где нельзя приложить ни одной из математических наук, и в том, что не имеет связи с математикой
Леонардо да Винчи,
G.36v (Записная книжка)
Глава 1
ПРЕДЕЛЫ
Если для <e, то . Практическое вычисление пределов основывается на следующих теоремах: Если существуюти тоГлава 2
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ
ОДНОЙ НЕЗАВИСИМОЙ ПЕРЕМЕННОЙ
Понятие производной
Производной от функции по аргументу называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к… ,Или
.
Примечание.
Производная обозначается так же, как 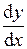 (Читается «дэ игрек по дэ икс».) Штрихом производная обозначается только в том случае, если она берется по
(Читается «дэ игрек по дэ икс».) Штрихом производная обозначается только в том случае, если она берется по 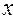 .
.
Отыскание производной называется дифференцированием функции.
Исходя из определения производной можно найти производную любой дифференцируемой функции.
Рассмотрим несколько примеров.
1. Найти производную функции
 . (1)
. (1)
Дадим  приращение
приращение  , тогда
, тогда 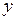 получит приращение
получит приращение  :
:
 ,
,
отсюда
 .
.
Функция 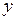 задается формулой (1).
задается формулой (1).
Тогда

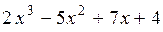 =
=
= 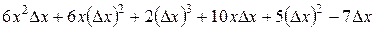 .
.
Находим отношение приращения функции к приращению аргумента:
 =
= .
.
Найдем предел этого отношения при  :
:
 =
= (
( )=
)= .
.
Следовательно, по определению производной,

 .
.
2. Найти производную функции
 . (2)
. (2)
Находим приращение функции 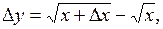 отсюда
отсюда
 =
=
и
=.
Таким образом,

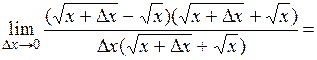

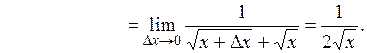
Итак,
 .
.
3. Найти производную функции
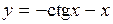 (3)
(3)
Находим приращение функции
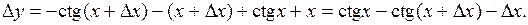
Воспользуемся формулой

Отсюда


и

 =
= .
.
Итак,

 =
= .
.
Исходя из определения производной найти производные следующих функций:
| 2.1. | 
| Ответ: -
|
| 2.2. | 
| Ответ: 
|
| 2.3. | 
| Ответ: 
|
| 2.4. | 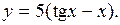
| Ответ: 
|
| 2.5. | 
| Ответ:
|
| 2.6. |  . .
| Ответ: 
|
| 2.7. |  . .
| Ответ: 
|
| 2.8. |  . .
| Ответ: 6∙(x-1) |
Основные правила дифференцирования.
Дифференцирование основных элементарных функций
Основные правила дифференцирования Пусть C –постоянная, - функции, имеющие производные, тогда: 1.Дифференцирование сложной функции
Пусть и - дифференцируемые функции. Тогда сложная функция есть также дифференцируемая функция, причем . Это правило распространяется на цепочку из любого конечного числа дифференцируемых функций: производная сложной…Производные высших порядков
. Производная третьего порядка (третья производная) от функции есть производная… .Дифференциал функции
Дифференциалом (первого порядка) функции называется главная часть ее приращения, линейная относительно приращения аргумента. Дифференциалом аргумента называется приращение этого аргумента: Дифференциал функции равен произведению ее производной на дифференциал аргумента:Имеем
 - дифференциал первого порядка,
- дифференциал первого порядка,
 - дифференциал второго порядка.
- дифференциал второго порядка.
3. Вычислить приближенное значение  .
.
Рассмотрим функцию . Полагая
. Полагая 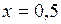 ,
,  и применяя формулу
и применяя формулу  , получаем
, получаем
 .
.
4. Вычислить приближенное значение площади круга, радиус которого равен 3,02 м.
Воспользуемся формулой  . Полагая R=3,
. Полагая R=3,  , имеем
, имеем
 .
.
Следовательно, площадь круга радиуса 3,02м имеет приближенное значение
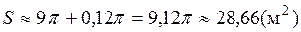 .
.
5. Вычислить приближенно  .
.
Рассмотрим функцию  и положим x=8,
и положим x=8, 
Тогда, воспользовавшись формулой  ,
,
найдем
 .
.
 .
.
Таким образом,  »2,0008.
»2,0008.
6. На сколько увеличилось ребро куба, если объем его изменился с 27 м3 до 27,2 м3?
Если 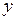 - ребро куба, то его объем
- ребро куба, то его объем 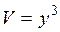 . Задача сводится к отысканию приращения
. Задача сводится к отысканию приращения  функции
функции  при
при  и
и 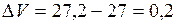 .
.
Приращение  найдем исходя из приближенного равенства
найдем исходя из приближенного равенства
 . Подставляем соответствующие значения и получаем
. Подставляем соответствующие значения и получаем
 (м).
(м).
Найти дифференциалы следующих функций:
| 2.141. |  . .
| Ответ:  . .
|
| 2.142. |  . .
| Ответ:  . .
|
| 2.143 |  . .
| Ответ:  . .
|
| 2.144. | 
| Ответ . .
|
Найти дифференциалы первого, второго и третьего порядков:
| 2.145. |  . .
| Ответ:  ; ;  ; ;  . .
|
| 2.146. |  . .
| Ответ:  ; ;  ; ; . .
|
| 2.147. |  . .
| Ответ:  ; ;  ; ;  . .
|
| 2.148. |  . .
| Ответ:  ; ;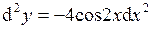 ; ;  . .
|
2.149. Найти приращение и дифференциал функции 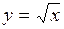 при
при  и
и 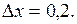 Вычислить абсолютную и относительную погрешности, которые получаются при замене функции ее дифференциалом. ( Ответ:
Вычислить абсолютную и относительную погрешности, которые получаются при замене функции ее дифференциалом. ( Ответ:  ;
;  ;
;  ).
).
2.150. Вычислить  и
и  для функции
для функции  при
при 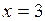 и
и  ( Ответ:
( Ответ:  ;
;  ).
).
2.151. Найти приращение и дифференциал функции  при
при 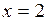 и
и  Вычислить абсолютную и относительную погрешности, которые получаются при замене функции ее дифференциалом.
Вычислить абсолютную и относительную погрешности, которые получаются при замене функции ее дифференциалом.
(Ответ: ;
; ;
; 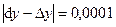 ;
;  ).
).
2.152. На сколько изменится сторона квадрата, если его площадь уменьшится с 16 м2 до 15,82 м2? (Ответ:0,0225 м)
2.153. Найти приближенное значение объема шара радиусом R=2,01 м. (Ответ: 34,04 м3).
2.154. Найти приближенное значение  . (Ответ:
. (Ответ: )
)
2.155. Найти приближенное значение  .(Ответ:2,999)
.(Ответ:2,999)
2.156. Найти приближенное значение  .(Ответ:1,035)
.(Ответ:1,035)
2.157. Найти приближенное значение 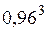 . (Ответ:0,88)
. (Ответ:0,88)
2.158. Поверхностная энергия жидкости рассчитывается по формуле  . Здесь
. Здесь  - энергия единицы площади, равная коэффициенту поверхностного натяжения,
- энергия единицы площади, равная коэффициенту поверхностного натяжения, 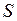 - площадь свободной поверхности жидкости. Найти изменение поверхностной энергии мыльного пузыря при увеличении его радиуса с 5 см до 5,2 см (площадь поверхности сферы
- площадь свободной поверхности жидкости. Найти изменение поверхностной энергии мыльного пузыря при увеличении его радиуса с 5 см до 5,2 см (площадь поверхности сферы  ). Коэффициент поверхностного натяжения мыльной воды в условиях данной задачи принять равным 0,04 Дж/м2 . (Ответ:
). Коэффициент поверхностного натяжения мыльной воды в условиях данной задачи принять равным 0,04 Дж/м2 . (Ответ:  Дж).
Дж).
2.159. Резиновый шар наполняется газом. Найти приближенно абсолютное и относительное изменение поверхности шара при увеличении его радиуса от 10,0 см до 10,5 см.
(Ответ: м2;
м2; 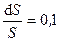 )
)
2.160. Период колебания математического маятника  , где
, где 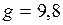 м/с2, а
м/с2, а  см. Найти изменение периода колебаний при уменьшении длины на 1 см. (Ответ:
см. Найти изменение периода колебаний при уменьшении длины на 1 см. (Ответ: 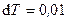 с)
с)
2.161. Разность потенциалов между внутренней частью клетки и внешней средой обусловлена различием концентрации ионов внутри  и вне
и вне  клетки. Величина этой разности потенциалов в милливольтах для одновалентных ионов при температуре 180 определяется формулой
клетки. Величина этой разности потенциалов в милливольтах для одновалентных ионов при температуре 180 определяется формулой  , где
, где 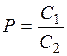 .
.
Рассчитать изменение  при увеличении
при увеличении  от 20 до 22. Учесть, что
от 20 до 22. Учесть, что 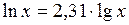 . (Ответ:
. (Ответ:  мВ).
мВ).
Применение производной при решении
Прикладных задач
В частности, если зависимость между пройденным путем и временем при прямолинейном движении выражается формулой , то скорость движения в любой момент… Примеры. 1. Точка движется прямолинейно по закону , где выражается в метрах, а - в секундах. (Обратите внимание на то, что…Решение. Скорость прямолинейного движения
Подставим значение =1с и получим (м/с). Ускорение прямолинейного движения равно второй производной пути по времени и,… 2. Тело вращается вокруг неподвижной оси так, что угол его поворота меняется с течением времени по закону , где A, B,…Глава 3
Исследование функций методами
Дифференциального исчисления
Интервалы монотонности функции
Как возрастающие, так и убывающие функции называются монотонными. Монотонность функции характеризуется знаком первой производной . Если в некотором… Рассмотрим примеры. 1. Даны функция и точки . В каких из перечисленных точек функция возрастает? Убывает?Решение.
Найдем производную заданной функции: .
при <0 - функция убывает, при >0 - функция возрастает, при <0 - функция убывает.Экстремум функции
Точки максимума и минимума функции называются точками ее экстремума, а значение функции в точке максимума (минимума) – максимумом (минимумом), или… Правила отыскания экстремумов функции:Глава 4
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ[4]
Непосредственное интегрирование
Функция называется первообразной для функции , еслиИнтегрирование способом подстановки
Способ подстановки заключается в том, чтобы, преобразовав подынтегральную…Интегрирование по частям
С помощью формулы интегрирования по частям
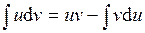 ,
,
где u, v –дифференцируемые функции, зависящие от х, нахождение интеграла  сводится к отысканию более простого интеграла
сводится к отысканию более простого интеграла  .
.
Примеры.
1. Найти интеграл
 .
.
Положим
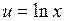 ,
,
тогда
 .
.
Отсюда

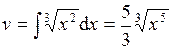 .
.
Используя формулу интегрирования по частям, получим

2. Найти интеграл

Полагая

найдем

Отсюда
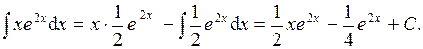
3. Найти интеграл
 .
.
Полагая

получим

Тогда интеграл примет вид:

Используя формулу интегрирования по частям, найти следующие интегралы:
| 4.41 | 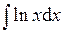
| 4.47 | 
|
| 4.42 | 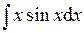
| 4.48 | 
|
| 4.43 | 
| 4.49 | 
|
| 4.44 | 
| 4.50 | 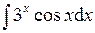
|
| 4.45 | 
| 4.51 | 
|
| 4.46 | 
| 4.52 | 
|
Применение неопределенного интеграла при решении прикладных задач
1. Шкив вращается вокруг оси под действием момента сил М, который меняется с течением времени по закону М=Аt, А- известная постоянная величина.… Используем для решения основное уравнение динамики вращения телаГлава 5
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Определенный интеграл и его непосредственное
Интегрирование
Определенным интегралом в пределах от а до b от функции f(x), непрерывной на отрезке [a,b], называется приращение любой ее первообразной F(x) при… . Основные свойства определенного интегралаПриложение определенного интеграла для вычисления площадей плоских фигур
Площадь S криволинейной трапеции, ограниченной непрерывной кривой 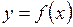 , двумя прямыми x=a и x=b и отрезком оси абсцисс
, двумя прямыми x=a и x=b и отрезком оси абсцисс 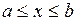 , вычисляется по одной из следующих формул:
, вычисляется по одной из следующих формул:
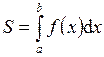 , если
, если  на отрезке
на отрезке  ;
;
 , если
, если  на отрезке
на отрезке  .
.
Площадь S фигуры, ограниченной двумя непрерывными кривыми и
и  и двумя прямыми x=a и x=b, где
и двумя прямыми x=a и x=b, где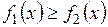 на отрезке
на отрезке , вычисляется по формуле
, вычисляется по формуле
 .
.
Рассмотрим примеры.
1. Вычислить площадь, ограниченную параболой  , прямыми x=2, x=4 и осью абсцисс.
, прямыми x=2, x=4 и осью абсцисс.
Площадь вычислим, используя формулу 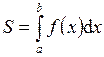 . Тогда
. Тогда

2. Вычислить площадь фигуры, ограниченной прямыми 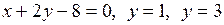 и осью ординат (рис.3).
и осью ординат (рис.3).
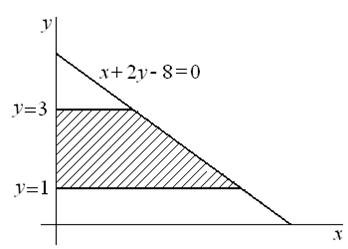
|
| Рис. 3 |
При вычислении искомой площади учтем, что изменены роли осей координат, т.е.:
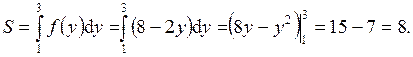
3. Вычислить площадь фигуры, ограниченной ветвью гиперболы  , прямыми x= -3, x= -1 и осью абсцисс.
, прямыми x= -3, x= -1 и осью абсцисс.
На отрезке  функция
функция  отрицательна. Поэтому для вычисления площади рассматриваемой фигуры воспользуемся формулой
отрицательна. Поэтому для вычисления площади рассматриваемой фигуры воспользуемся формулой
 .
.
Получим

4. Вычислить площадь между линиями  .
.

|
| Рис.4 |
Искомая площадь изображена на рис. 4 и представляет собой разность между площадью прямоугольного треугольника OMx0 и площадью криволинейного треугольника, ограниченного сверху участком параболы:
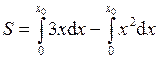 .
.
Абсциссу x0 точки пересечения графиков находим, решая совместно уравнения  , откуда
, откуда  .
.
Подставляя полученное значение верхнего предела интегрирования, получаем

5.31 Вычислить площадь, ограниченную гиперболой , осью абсцисс и ординатами
, осью абсцисс и ординатами  .
.
5.32 Вычислить площадь фигуры, заключенной между линиями  . Изобразить фигуру графически.
. Изобразить фигуру графически.
5.33 Найти площадь фигуры, заключенной между осью абсцисс и кривой  .
.
5.34 Найти площадь фигуры, ограниченной кривой  , прямыми
, прямыми  и осью абсцисс.
и осью абсцисс.
5.35 Вычислить площадь фигуры, образованной линиями  .
.
5.36 Определить площадь фигуры, ограниченной параболой  и прямой
и прямой  .
.
5.37 Найти площадь фигуры, заключенной между прямыми  и осью абсцисс.
и осью абсцисс.
5.38 Вычислить площадь между линиями 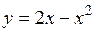 и
и  .
.
5.39 Определить площадь, ограниченную экспонентой 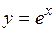 , осью абсцисс и ординатами
, осью абсцисс и ординатами  .
.
5.40 Найти площадь фигуры, ограниченной параболой  , осью абсцисс и прямыми
, осью абсцисс и прямыми  .
.
Приложение определенного интеграла к решению физических задач
Рассмотрим решение следующих задач.
1. Через участок тела животного проходит импульс тока, который изменяется со временем по закону  мА. Длительность импульса 0,1 с. Определить работу, совершаемую током за это время, если сопротивление участка равно 20 кОм.
мА. Длительность импульса 0,1 с. Определить работу, совершаемую током за это время, если сопротивление участка равно 20 кОм.
За малый интервал времени dt, когда ток практически не меняется, на сопротивлении R совершается работа  . За время всего импульса будет совершена работа
. За время всего импульса будет совершена работа
 .
.
Подставляя в полученное выражение значение тока, получим.
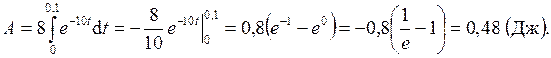
2. Скорость точки равна  (м/с). Найти путь S, пройденный точкой за время t=4с, прошедшее от начала движения.
(м/с). Найти путь S, пройденный точкой за время t=4с, прошедшее от начала движения.
Найдем путь 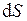 , пройденный точкой за бесконечно малый промежуток времени
, пройденный точкой за бесконечно малый промежуток времени  . Так как в течение этого времени скорость можно считать постоянной, то
. Так как в течение этого времени скорость можно считать постоянной, то 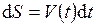 . Интегрируя, имеем
. Интегрируя, имеем
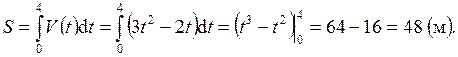
3. Найти силу давления жидкости на вертикальную треугольную пластину с основанием a и высотой h, погруженную в жидкость так, что ее вершина лежит на поверхности.
Систему координат расположим, как показано на рис. 5.

|
| Рис. 5 |
Рассмотрим горизонтальную бесконечно малую полоску толщиной dx, находящуюся на произвольной глубине x. Принимая эту полоску за прямоугольник, найдем ее основание EF. Из подобия треугольников ABC и AEF получаем
 .
.
Отсюда
 .
.
Тогда площадь полоски равна
 .
.
Так как сила P давления жидкости на площадку S, глубина погружения которой r, по закону Паскаля равна
 ,
,
где r- плотность жидкости, g- ускорение силы тяжести, то искомая сила давления на рассматриваемую площадку dS вычисляется по формуле
 .
.
Следовательно, сила давления P жидкости на площадку ABC
 .
.
Решить задачи.
5.41 Скорость движения точки определяется уравнением  см/с. Найти путь, пройденный точкой за время t=5с, протекшее от начала движения.
см/с. Найти путь, пройденный точкой за время t=5с, протекшее от начала движения.
5.42 Скорость тела выражается формулой  м/с. Найти путь, пройденный телом за первые три секунды после начала движения.
м/с. Найти путь, пройденный телом за первые три секунды после начала движения.
5.43 Скорость движения тела определяется уравнением  см/с. Какой путь пройдет тело за третью секунду движения?
см/с. Какой путь пройдет тело за третью секунду движения?
5.44 Два тела начинают двигаться одновременно из одной и той же точки: одно со скоростью  (м/мин), а другое со скоростью
(м/мин), а другое со скоростью  (м/мин). На каком расстоянии друг от друга они будут через 10 мин, если двигаются по одной линии в одном направлении?
(м/мин). На каком расстоянии друг от друга они будут через 10 мин, если двигаются по одной линии в одном направлении?
5.45 На тело массой 5 г, движущееся прямолинейно, действует сила 
 (дин). Найти расстояние, пройденное телом в течение третьей секунды движения.
(дин). Найти расстояние, пройденное телом в течение третьей секунды движения.
5.46 Скорость колеблющейся точки изменяется по закону  (см/с). Определить смещение точки через 0,1 с после начала движения.
(см/с). Определить смещение точки через 0,1 с после начала движения.
5.47 Какую работу нужно совершить, чтобы растянуть пружину на 0,06 м, если сила в 1Н растягивает ее на 0,01 м?
5.48 Скорость колеблющейся точки изменяется по закону  (м/с). Определить путь, пройденный точкой за
(м/с). Определить путь, пройденный точкой за  с от начала движения.
с от начала движения.
5.49 Азот, масса которого 7 г, расширяется при неизменной температуре, равной 300°К так, что его объем увеличивается вдвое. Определить работу, совершаемую газом. Универсальная газовая постоянная  Дж/кмоль.
Дж/кмоль.
5.50 Какую работу надо совершить, чтобы растянуть пружину длиной в 25 см до длины в 35 см, если известно, что коэффициент жесткости пружины равен 400 Н/м?
5.51 Через тело животного проходит импульс тока, который изменяется со временем по закону  (мА). Длительность импульса равна 0,1с. Определить заряд, протекающий через тело животного.
(мА). Длительность импульса равна 0,1с. Определить заряд, протекающий через тело животного.
5.52 Какая работа совершается при растяжении мышцы на l мм, если известно, что при нагрузке P0 мышца растягивается на l0 мм? Считать, что сила, необходимая для растяжения мышц, пропорциональна ее удлинению.
5.53 Тело двигается в некоторой среде прямолинейно по закону  . Сопротивление среды пропорционально квадрату скорости
. Сопротивление среды пропорционально квадрату скорости  . Найти работу, произведенную силой сопротивления среды при передвижении тела от S=0 до S=a метров.
. Найти работу, произведенную силой сопротивления среды при передвижении тела от S=0 до S=a метров.
Глава 6
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Основные понятия
Уравнение, связывающее независимую переменную, неизвестную функцию и ее производные или дифференциалы различных порядков, называется дифференциальным уравнением.
Порядком дифференциального уравнения называется порядок старшей производной, входящей в это уравнение. Например, уравнение  - первого порядка.
- первого порядка.
Функция y=j(x), удовлетворяющая дифференциальному уравнению, называется решением этого уравнения.
Решение дифференциального уравнения, содержащее столько независимых произвольных постоянных, каков порядок уравнения, называется общим решением этого уравнения.
Например, для уравнения первого порядка общее решение имеет вид y=j(x,с).
Функции, получаемые из общего решения при различных числовых значениях произвольных постоянных, называются частными решениями.
Для нахождения частного решения дифференциального уравнения задаются начальные условия.
Рассмотрим следующие примеры.
1. Проверить, является ли функция y=cos x решением уравнения
y²+y=0.
Найдем y¢=-sin x, y²=-cos x. Подставляя выражения для y² и y в данное уравнение, получаем
y²+y=-cos x+ cos x=0,
т.е. функция y=cos x является решением данного дифференциального уравнения.
2. Общее решение дифференциального уравнения y¢-3y=0 имеет вид
y=Ce3x.
Найти его частное решение, удовлетворяющее начальному условию y(1)=e3.
Значение произвольной постоянной С, соответствующее некому частному решению, получается в результате подстановки в выражение общего решения заданных начальных условий: e3=Ce3, откуда С=1. Подставляя полученное значение С=1 в общее решение, найдем частное решение y=e3x, удовлетворяющее заданным начальным условиям.
6.1 Выяснить, являются ли решениями дифференциального уравнения  следующие функции:
следующие функции:
a. 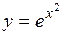 ;
;
b. 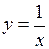 ;
;
c.  ;
;
d.  .
.
6.2 Выяснить, являются ли решениями дифференциального уравнения  следующие функции:
следующие функции:
a.  ;
;
b.  ;
;
c.  ;
;
d.  .
.
6.3 Общее решение дифференциального уравнения 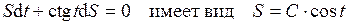 .
.
Найти частное решение, удовлетворяющее начальным условиям  .
.
Уравнения с разделяющимися переменными
Дифференциальное уравнение с разделяющимися переменными имеет вид
 .
.
Поделив все члены уравнения на  , получим уравнение
, получим уравнение
 ,
,
в котором переменные разделены.
Общее решение уравнения находим почленным интегрированием

Например.
1. Найти общее решение уравнения
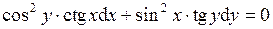 .
.
Поделим обе части уравнения на  :
:
 .
.
Интегрируя обе части уравнения, получим
 ,
,
откуда
 .
.
Так как С- произвольная постоянная, то ее можно заменить на 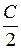 . Тогда
. Тогда
 ,
,
это и есть общее решение данного уравнения.
2. Найти частное решение дифференциального уравнения  , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям  .
.
Найдем общее решение данного уравнения. Для этого разделим переменные:
 ,
,
или
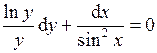 .
.
Интегрируя, получаем
 .
.
Используя начальные условия, подставляем в выражение общего решения заданные значения переменных  , тем самым определяем значение производной постоянной С:
, тем самым определяем значение производной постоянной С:
 .
.
Из последнего равенства получаем С = -1.
Итак, искомое частное решение :
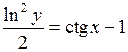 .
.
Найти общее решение дифференциальных уравнений.
| 6.4 | 
| 6.8 | 
|
| 6.5 | 
| 6.9 | 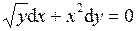
|
| 6.6 | 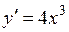
| 6.10 | 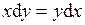
|
| 6.7 | 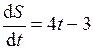
| 6.11 | 
|
Найти общее и частное решение дифференциальных уравнений:
| 6.12 |  ,
если ,
если  . .
| 6.15 |  ,
если ,
если  . .
|
| 6.13 |  ,
если ,
если  . .
| 6.16 |  ,
если ,
если 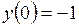 . .
|
| 6.14 |  ,
если ,
если  . .
| 6.17 |  ,
если ,
если 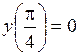 . .
|
Однородные дифференциальные уравнения
Однородное уравнение приводится к уравнению с разделяющимися переменными подстановкой y=Ux, где U- новая искомая функция. Дифференцируя равенство… . Подставив выражения y и в уравнение, имеемЗадачи на составление дифференциальных уравнений
Скорость распада радия пропорциональна его имеющемуся количеству R. Найти закон распада радия, если известно, что через 1600 лет останется половина… Решение. Пусть R- количество радия в момент времени t, а R0- его…Глава 7
Элементы теории вероятностей
И математической статистики
Основные понятия
Теория вероятностей и методы математической статистики широко используются при изучении заболеваемости, физического развития населения, физиологических и биохимических показателей. Это обусловлено тем, что многим биологическим явлениям свойственны статистические закономерности, которые обнаруживаются при изучении случайных совокупностей.
Теория вероятностей изучает закономерности, присущие массовым (статистическим) случайным событиям, и их количественную оценку. Математическая статистика позволяет систематизировать и оценивать экспериментальные данные, которые рассматриваются как случайные величины.
Важнейшими понятиями теории вероятностей и математической статистики являются понятия «случайное событие», «вероятность случайного события», «случайная величина».
Случайным событием А называют событие, которое в одинаковых условиях эксперимента может произойти, а может и не произойти, и о появлении которого не может быть сделано точного предсказания.
Вероятность случайного события – это количественная оценка объективной возможности появления данного события.
, где – количество появлений события А. Переменные величины, которые принимают различные значения в зависимости от стечения случайных обстоятельств, называют…Числовые характеристики распределения
Случайных величин
Математическое ожидание – наиболее вероятное значение случайной величины. Для дискретных величин оно равняется сумме произведений каждого возможного… , (3) где n-количество значений случайной величины.Нормальный закон распределения случайных величин
Существуют различные законы распределения случайных величин. Для непрерывных величин наиболее распространенным является так называемый нормальный закон распределения или закон Гаусса. В соответствии с этим законом распределяются масса тела, рост человека, физиологические показатели и многое другое. В ряде случаев этот закон применим для анализа распределений дискретных случайных величин.
Функция плотности вероятностей нормального закона распределения случайных величин имеет следующий вид:
 , (9)
, (9)
где  – основание натурального логарифма,
– основание натурального логарифма, 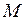 – математическое ожидание
– математическое ожидание  ,
,  среднее квадратичное отклонение случайной величины
среднее квадратичное отклонение случайной величины  .
.
График этой зависимости называется кривой нормального закона распределения, или кривой Гаусса (рис.1). Кривая имеет колоколообразную форму, она симметрична и асимптотически приближается к нулю. Из рисунка видно, что наиболее вероятным значением случайной величины является математическое ожидание 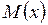 . При отклонении величины
. При отклонении величины  в большую или меньшую сторону вероятность ее уменьшается.
в большую или меньшую сторону вероятность ее уменьшается.
 Рис. 1
Рис. 1
На кривой имеются две характерные точки, где выпуклость ее переходит в вогнутость. Абсциссы этих точек равны  и
и 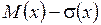 .
.
Таблица 1
| Интервал | Р,% | ||||

| 
| 
| 68,3 | ||

| 
| 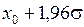
| 95,0 | ||

| 
| 
| 95,5 | ||

| 
| 
| 99,0 | ||

| 
| 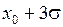
| 99,7 | ||
Здесь через 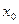 обозначено обозначено 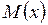 . .
| |||||
Зная функцию плотностей вероятностей, можно рассчитать вероятность попадания случайной величины в заданный интервал значений 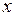 . Например, вероятность попадания в интервал между значениями
. Например, вероятность попадания в интервал между значениями 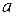 и
и  равна:
равна:
 ,
,
или, графически, вероятность попадания оказывается равной площади криволинейной трапеции, заштрихованной на графике, приведенном на рис.1,в.
Рассчитано (табл.1), что вероятность появления случайной величины в интервале  составляет 0,68, в интервале
составляет 0,68, в интервале  – примерно 0,95, а в интервале
– примерно 0,95, а в интервале  вероятность появления случайной величины составляет 0,997.
вероятность появления случайной величины составляет 0,997.
Генеральная совокупность.
Оценка параметров генеральной совокупности по ее выборке
Однако в реальных условиях эксперимента невозможно изучить всю совокупность значений случайной величины – генеральную совокупность, поэтому… Часть значений случайной величины, которая отобрана для изучения, называется… Отдельные значения случайной величины называются вариантамиИнтервальная оценка. Интервальная оценка
Точечная оценка, особенно при малой выборке, может значительно отличаться от истинных параметров генеральной совокупности. При небольшом объеме… В этом случае указывается интервал (доверительный интервал или доверительные… Иначе говоря, определяет вероятность, с которой осуществляются следующие неравенства:Проверка гипотез. Критерии значимости
В этом случае для анализа используется так называемый t-тест, или t-критерий Стьюдента, который называют еще критерием достоверности, или критерием… В рассматриваемом нами случае t-критерий можно рассчитать как ,Элементы корреляционного и регрессионного анализа
7.1. Характер взаимосвязи между признаками Все многообразие связей между отдельными признаками, свойствами явлений или параметрами функционирующего объекта можно…ЛАБОРАТОРНЫЕ РАБОТЫ
ПО СТАТИСТИЧЕСКОЙ ОБРАБОТКЕ РЕЗУЛЬТАТОВ
I. Статистическая обработка данных измерения роста
1.Взять результаты измерений роста[5] 100 человек, сведенные в вариационный ряд (см. приложение) и перенести их в таблицу 1 (100 измерений взято для… Таблица 1 № варианты Значение варианты xi Частота варианты li xili 1. …II. Провести статистический анализ для следующих совокупностей данных
2.2. Измерен диаметр эритроцитов у кролика (размер дан в микрометрах):6,0; 5,6; 5,6; 6,8; 7,4; 6,0; 7,9; 7,4; 6,3; 6,3; 6,8; 7,2; 6,0; 6,3; 6,3;… 2.3. Проведены измерения систолического давления у мужчины в начальной стадии… Рассчитать среднее значение систолического давления, дисперсию, среднеквадратичное отклонение, среднюю ошибку среднего…ОТВЕТЫ
| Глава 4 | |||
| 4.1 | 
| 4.2 | 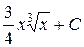
|
| 4.3 | 
| 4.4 | 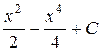
|
| 4.5 | 
| 4.6 | 
|
| 4.7 | 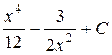
| 4.8 | 
|
| 4.9 | 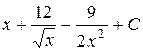
| 4.10 | 
|
| 4.11 | 
| 4.12 | 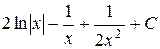
|
| 4.13 | 
| 4.14 | 
|
| 4.15 | 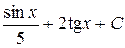
| 4.16 | 
|
| 4.17 | 
| 4.18 | 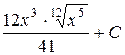
|
| 4.19 | 
| 4.20 | 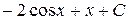
|
| 4.21 | 
| 4.22 | 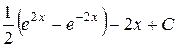
|
| 4.23 | 
| 4.24 | 
|
| 4.25 | 
| 4.26 | 
|
| 4.27 | 
| 4.28 | 
|
| 4.29 | 
| 4.30 | 
|
| 4.31 | 
| 4.32 | 
|
| 4.33 | 
| 4.34 | 
|
| 4.35 | 
| 4.36 | 
|
| 4.37 | 
| 4.38 | 
|
| 4.39 | 
| 4.40 | 
|
| 4.41 | 
| 4.42 | 
|
| 4.43 | 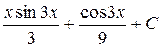
| 4.44 | 
|
| 4.45 | 
| 4.46 | 
|
| 4.47 | 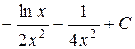
| 4.48 | 
|
| 4.49 | 
| 4.50 | 
|
| 4.51 | 
| 4.52 | 
|
| 4.53 | 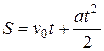
| 4.54 | 
|
| 4.55 | 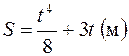
| 4.56 | 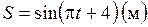
|
| 4.57 | 
| 4.58 | 
|
| 4.59 | 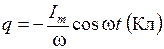
| 4.60 | 
|
| Глава 5 | |
| 5.1 | 
|
| 5.2 | 
|
| 5.3 | 
|
| 5.4 | 
|
| 5.5 | 
|
| 5.6 | |
| 5.7 | 1/4 |
| 5.8 | |
| 5.9 | 
|
| 5.10 | 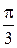
|
| 5.11 | |
| 5.12 | 
|
| 5.13 | 
|
| 5.14 | 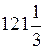
|
| 5.15 | 
|
| 5.16 | 
|
| 5.17 | 
|
| 5.18 | 
|
| 5.19 | 
|
| 5.20 | 
|
| 5.21 | 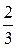
|
| 5.22 | 0,24 |
| 5.23 | 
|
| 5.24 | |
| 5.25 | 
|
| 5.26 | 0,5 |
| 5.27 | 0,5 |
| 5.28 | 
|
| 5.29 | 1/3 |
| 5.30 | |
| 5.31 | |
| 5.32 | |
| 5.33 | 10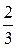
|
| 5.34 | 4,25 |
| 5.35 | 
|
| 5.36 | |
| 5.37 | |
| 5.38 | 
|
| 5.39 | » 2,33 |
| 5.40 | |
| 5.41 | 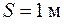
|
| 5.42 | 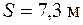
|
| 5.43 | 
|
| 5.44 | 
|
| 5.45 |  
|
| 5.46 | 
|
| 5.47 | 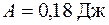
|
| 5.48 | 
|
| 5.49 | 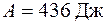
|
| 5.50 | 
|
| 5.51 | 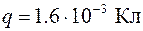
|
| 5.52 | 
|
| 5.53 | 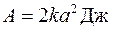
|
| Глава 6. | ||
| 6.1 | a). нет b). да | c). нет d). да |
| 6.2 | a). нет b). да | c). да d). да |
| 6.3 | S = -2cost | |
| 6.4 | 
| |
| 6.5 | 
| |
| 6.6 | 
| |
| 6.7 | 
| |
| 6.8 | 
| |
| 6.9 | 
| |
| 6.10 | 
| |
| 6.11 | 
| |
| 6.12 | 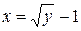
| |
| 6.13 | 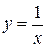
| |
| 6.14 | 
| |
| 6.15 | 
| |
| 6.16 | 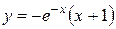
| |
| 6.17 | 
| |
| 6.18 | 
| |
| 6.19 | 
| |
| 6.20 | 
| |
| 6.21 | 
| |
| 6.22 | 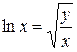
| |
| 6.23 | 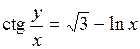
| |
| 6.24 | 
| |
| 6.25 | 
| |
| 6.26 | За 30 мин | |
| 6.27 | 1 см/с | |
| 6.28 | »44% | |
| 6.29 | 
| |
| 6.30 | 
| |
| 6.31 | 
| |
| 6.32 | 
| |
| 6.33 | 
|
СПИСОК ЛИТЕРАТУРЫ
1. Герасимов А.Н. Медицинская статистика: учебное пособие /- М.: МИА, 2007.-475с.
2. Кучеренко В.З.. Применение методов статистического анализа для изучения общественного здоровья и здравоохранения: учебное пособие для медицинских вузов /- М.: ГЭОТАР - Медиа, 2007.-245с.
3. Павлушков И.В. Основы высшей математики с математической статистикой: учебник для мед. и фармац. вузов /-Изд. 2-е, исправл.- М.: ГЭОТАР - Медиа, 2007.-422с.
4. Ремизов А.Н. , А.Я. Потапенков. Курс лекций: учебник / - Изд. 3-е.- М.: Дрофа, 2006.-720с.
5. Математическая статистика с основами высшей математики: учебник / В.И. Чернов [и др]. - Воронеж: ГОУ «Воронеж. гос. мед. акад. им Н.Н Бурденко» , 2006.-317с.
Учебно-методическое издание
УЧЕБНО-МЕТОДИЧЕСКОЕ ПОСОБИЕ к практическим занятиям по высшей математике и математической статистике
Г.Е.Кирко, Я.Р Кустова., А.Л. Афанасьев, А.Г.Корякина, З.А.Смирнова, Н.В.Зернина, Н.К Сазонова., М.Р.Черемных Редактор Н.А. Щепина– Конец работы –
Используемые теги: математической, статистике0.05
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Математической статистике
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов