рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Образование
- /
- Лабораторная работа №1 «Элементарная теория погрешностей»
Реферат Курсовая Конспект
Лабораторная работа №1 «Элементарная теория погрешностей»
Лабораторная работа №1 «Элементарная теория погрешностей» - раздел Образование, Лабораторная Работа №1 «Элементарная Теория Погрешностей»...
Лабораторная работа №1 «Элементарная теория погрешностей»
Задание 1.Выполнить последовательные округления следующих чисел:
1. а) 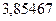 ; б)
; б) 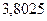 ; 16. а)
; 16. а) 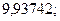 б)
б) 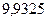 ;
;
2. а) 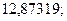 б)
б) 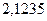 ; 17. а)
; 17. а) 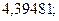 б)
б) 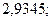
3. а) 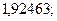 б)
б) 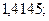 18. а)
18. а) 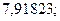 б)
б) 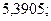
4. а) 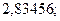 б)
б) 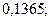 19. а)
19. а) 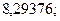 б)
б) 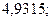
5. а) 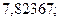 б)
б) 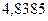 ; 20. а)
; 20. а) 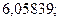 б)
б) 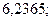
6. а) 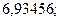 б)
б) 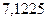 ; 21. а)
; 21. а) 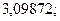 б)
б) 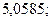
7. а) 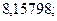 б)
б) 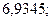 22. а)
22. а) 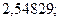 б)
б) 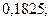
8. а) 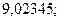 б)
б) 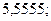 23. а)
23. а) 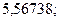 б)
б) 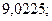
9. а) 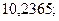 б)
б) 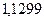 ; 24. а)
; 24. а) 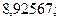 б)
б) 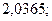
10. а) 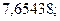 б)
б) 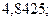 25. а)
25. а) 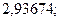 б)
б) 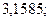
11. а) 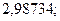 б)
б) 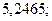 26. а)
26. а) 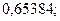 б)
б) 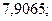
12. а) 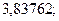 б)
б) 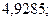 27. а)
27. а) 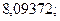 б)
б) 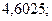
13. а) 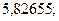 б)
б) 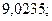 28. а)
28. а) 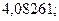 б)
б) 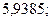
14. а) 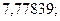 б)
б) 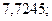 29. а)
29. а) 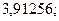 б)
б) 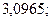
15. а) 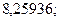 б)
б) 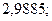 30. а)
30. а) 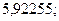 б)
б) 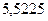 .
.
Задание 2.Определить, какое из равенств точнее.
1. 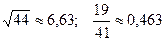 ; 16.
; 16. 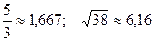 ;
;
2. 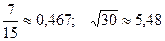 ; 17.
; 17. 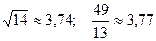 ;
;
3. 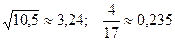 ; 18.
; 18. 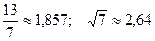 ;
;
4. 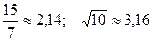 ; 19.
; 19. 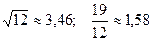 ;
;
5. 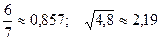 ; 20.
; 20. 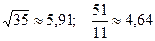 ;
;
6. 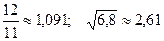 ; 21.
; 21. 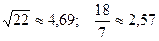 ;
;
7. 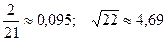 ; 22.
; 22. 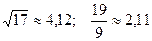 ;
;
8. 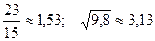 ; 23.
; 23. 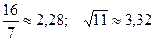 ;
;
9. 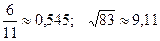 ; 24.
; 24. 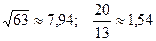 ;
;
10. 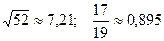 ; 25.
; 25. 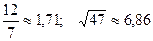 ;
;
11. 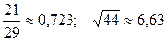 ; 26.
; 26. 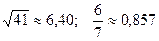 ;
;
12. 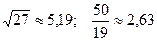 ; 27.
; 27. 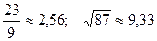 ;
;
13. 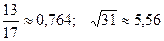 ; 28.
; 28. 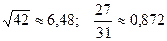 ;
;
14. 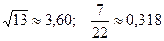 ; 29.
; 29. 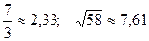 ;
;
15. 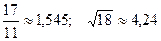 ; 30.
; 30. 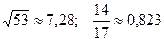 .
.
Пример 1.Выполнить последовательные округления следующих чисел:
а) 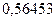 ; б)
; б) 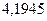 .
.
Решение.
а) 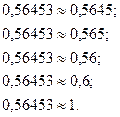 б)
б) 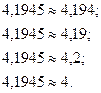
Пример 2. Определить, какое из равенств точнее: 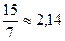 или
или 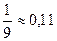 .
.
Решение.
Берем числа с большим числом десятичных знаков:
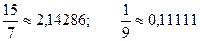 .
.
Определяем предельные абсолютные погрешности, округляя их с избытком:
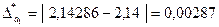 ;
;
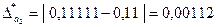 .
.
Находим предельные относительные погрешности:
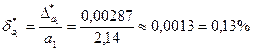 ;
;
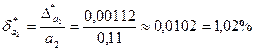 .
.
Т.к. 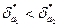 , то первое равенство точнее.
, то первое равенство точнее.
Лабораторная работа №2 «Элементарная теория погрешностей»
- Вычислить и определить погрешности результата.
- Вычислить и определить погрешности результата.
- Вычислить, пользуясь правилами подсчета цифр.
- а)
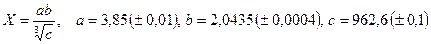 ; б)
; б) 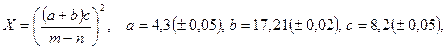
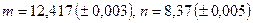 ; в)
; в) 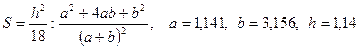 .
. - а)
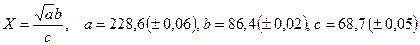 ; б)
; б) 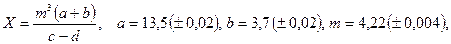
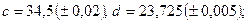 в)
в) 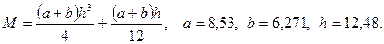
- а)
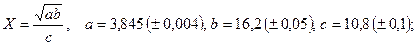 б)
б)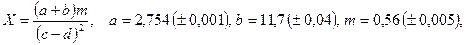
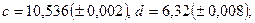 в)
в) 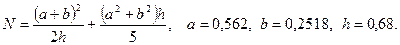
- а)
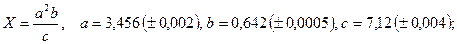 б)
б) 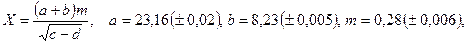
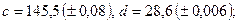 в)
в) 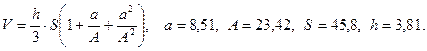
- а)
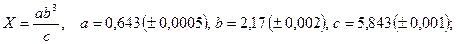 б)
б) 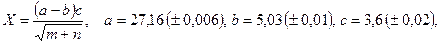
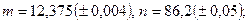 в)
в) 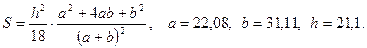
- а)
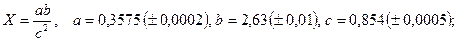 б)
б) 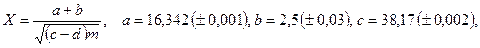
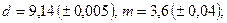 в)
в) 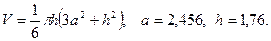
- а)
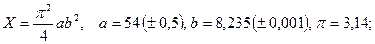 б)
б) 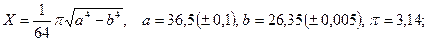 в)
в) 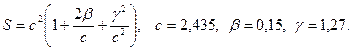
- а)
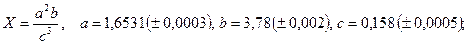 б)
б) 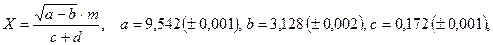
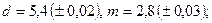 в)
в) 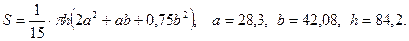
- а)
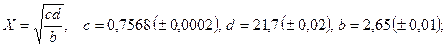 б)
б) 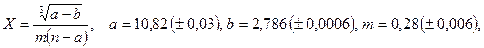
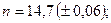 в)
в) 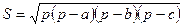 , где
, где 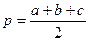 ,
, 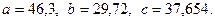
- а)
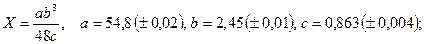 б)
б) 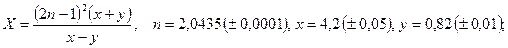 в)
в) 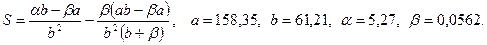
- а)
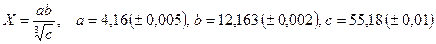 ; б)
; б) 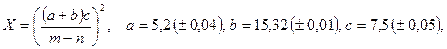
 ; в)
; в) 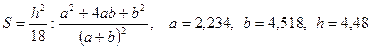 .
. - а)
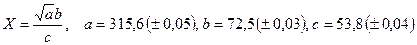 ; б)
; б) 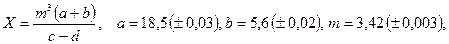
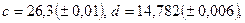 в)
в) 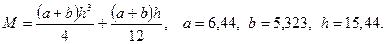
- а)
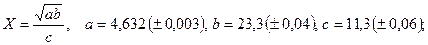 б)
б)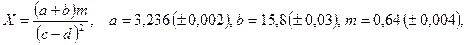
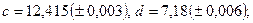 в)
в) 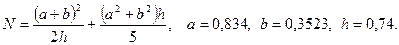
- а)
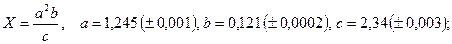 б)
б) 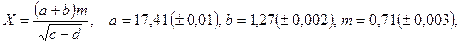
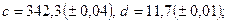 в)
в) 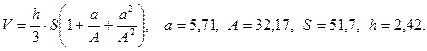
- а)
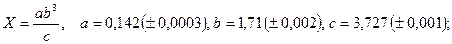 б)
б) 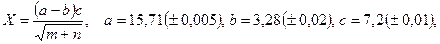
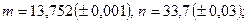 в)
в) 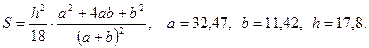
- а)
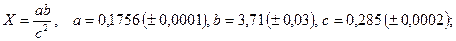 б)
б) 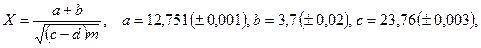
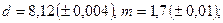 в)
в) 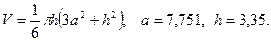
- а)
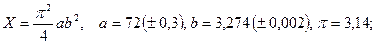 б)
б) 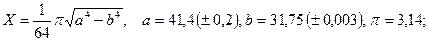 в)
в) 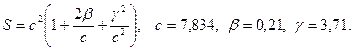
- а)
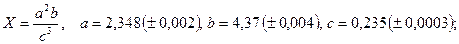 б)
б) 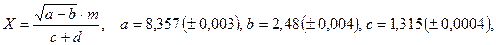
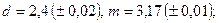 в)
в) 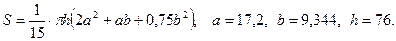
- а)
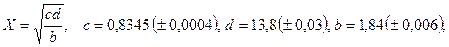 б)
б) 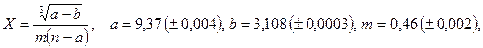
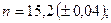 в)
в) 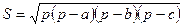 , где
, где 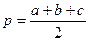 ,
, 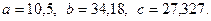
- а)
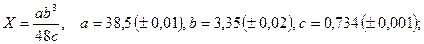 б)
б) 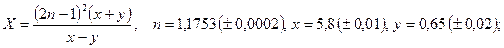 в)
в) 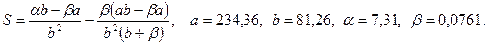
- а)
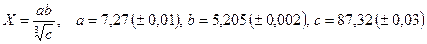 ; б)
; б) 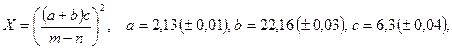
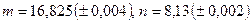 ; в)
; в) 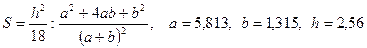 .
. - а)
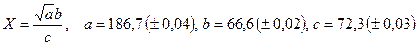 ; б)
; б) 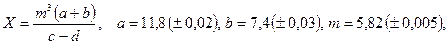
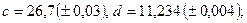 в)
в) 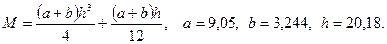
- а)
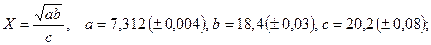 б)
б)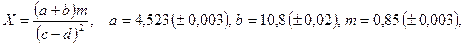
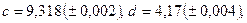 в)
в) 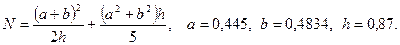
- а)
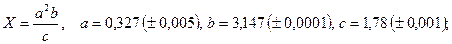 б)
б) 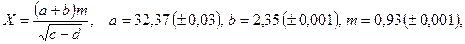
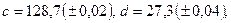 в)
в) 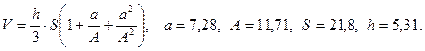
- а)
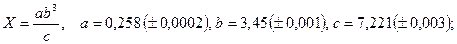 б)
б) 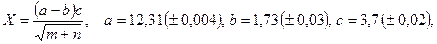
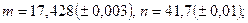 в)
в) 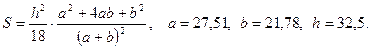
- а)
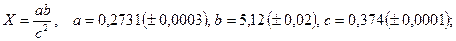 б)
б) 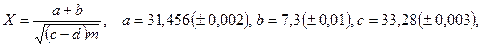
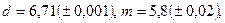 в)
в) 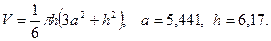
- а)
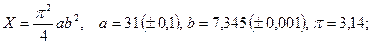 б)
б) 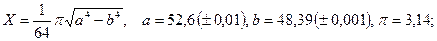 в)
в) 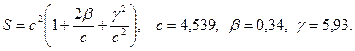
- а)
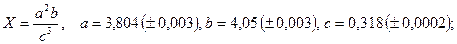 б)
б) 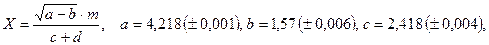
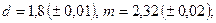 в)
в) 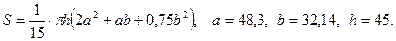
- а)
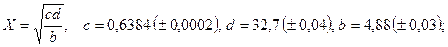 б)
б) 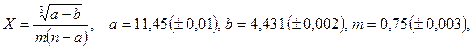
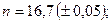 в)
в) 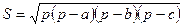 , где
, где 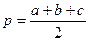 ,
, 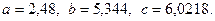
- а)
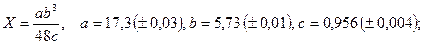 б)
б) 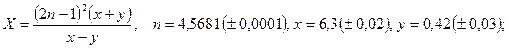 в)
в) 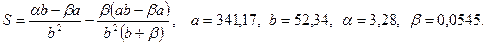
Пример 1.
Вычислить 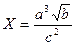 , где
, где 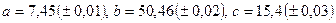 . Определить погрешность результата.
. Определить погрешность результата.
Решение.
При вычислении промежуточных результатов будем сохранять одну «запасную цифру», т.е. если по общему правилу следует оставить  значащих цифр, то в промежуточных результатах сохраним
значащих цифр, то в промежуточных результатах сохраним 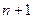 цифру. Тогда:
цифру. Тогда:
1) 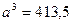
При возведении приближенного числа в степень в результате следует оставить столько верных значащих цифр, сколько верных значащих цифр содержится в основании степени. Т.к. в основании степени 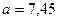 содержится три верных значащих цифры, то в результате оставляем четыре цифры (одну «запасную»).
содержится три верных значащих цифры, то в результате оставляем четыре цифры (одну «запасную»).
2) 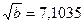
При извлечении корня 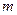 -й степени из приближенного числа, в результате следует брать столько значащих цифр, сколько верных значащих цифр имеет подкоренное выражение. Т.к. в подкоренном выражении
-й степени из приближенного числа, в результате следует брать столько значащих цифр, сколько верных значащих цифр имеет подкоренное выражение. Т.к. в подкоренном выражении 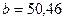 содержится четыре верных значащих цифры, то в результате оставляем пять верных значащих цифр (одна «запасная»).
содержится четыре верных значащих цифры, то в результате оставляем пять верных значащих цифр (одна «запасная»).
3) 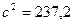
Т.к. в основании степени 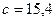 содержится три верных значащих цифры, то в результате оставляем четыре цифры (одну «запасную»).
содержится три верных значащих цифры, то в результате оставляем четыре цифры (одну «запасную»).
4) 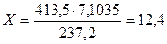
В результате оставлено три значащих цифры, т.к. наименьшее число значащих цифр в числах 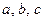 равно трем.
равно трем.
5) Находим предельную относительную погрешность, используя правила и определения: а) предельная относительная погрешность произведения равна сумме предельных относительных погрешностей сомножителей; б) предельная относительная погрешность частного равна сумме предельных относительных погрешностей делимого и делителя; в) предельная относительная погрешность 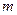 -й степени приближенного числа в
-й степени приближенного числа в 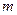 раз больше предельной относительной погрешности самого числа; г) предельная относительная погрешность корня
раз больше предельной относительной погрешности самого числа; г) предельная относительная погрешность корня 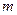 -й степени в
-й степени в 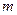 раз меньше предельной относительной погрешности подкоренного выражения; д)
раз меньше предельной относительной погрешности подкоренного выражения; д) 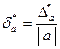 ; е)
; е) 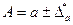 . Таким образом:
. Таким образом:
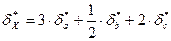
6) Находим предельную абсолютную погрешность: 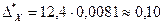
Ответ: 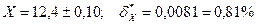 .
.
Пример 2. Вычислить 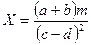 , где
, где 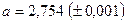 ,
, 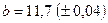 ,
, 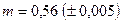 ,
, 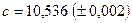 ,
, 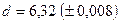 . Определить погрешность результата.
. Определить погрешность результата.
Решение.
1) 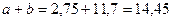
При сложении приближенных чисел в результате следует сохранить столько десятичных знаков, сколько их в приближенном данном с наименьшим числом десятичных знаков. При вычислении промежуточных результатов следует сохранить на одну цифру больше. Поэтому при сложении чисел 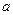 и
и 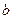 сохраняем две цифры после запятой.
сохраняем две цифры после запятой.
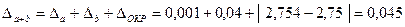
Полную погрешность находим как сумму абсолютных величин всех видов погрешностей.
2) 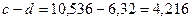
При вычитании приближенных чисел в результате следует сохранить столько десятичных знаков, сколько их в приближенном данном с наименьшим числом десятичных знаков. При вычислении промежуточных результатов следует сохранить на одну цифру больше. Поэтому при вычитании чисел 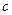 и
и 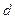 сохраняем три цифры после запятой.
сохраняем три цифры после запятой.
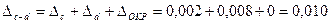
Полную погрешность находим как сумму абсолютных величин всех видов погрешностей.
3) 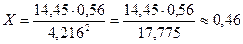
При возведении приближенного числа в квадрат в результате следует сохранить столько значащих цифр, сколько их в основании степени. При вычислении промежуточных результатов следует сохранить на одну цифру больше. Поэтому при вычислении 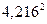 сохраняем пять значащих цифр.
сохраняем пять значащих цифр.
При умножении и делении в результате следует сохранить столько значащих цифр, сколько их в приближенном данном с наименьшим числом верных значащих цифр. Поэтому результат округляем до двух значащих цифр.
4) Относительная погрешность:
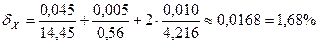 .
.
5) Абсолютная погрешность:
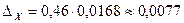 .
.
Ответ: 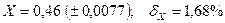 .
.
Пример 3. Пользуясь правилами подсчета цифр, вычислить 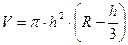 , где
, где 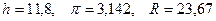 .
.
Решение.
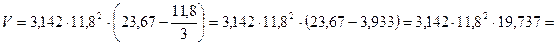
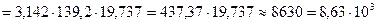 .
.
Ответ: 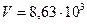 .
.
При вычислениях используем правила:
- При вычислениях промежуточных результатов следует сохранять на одну цифру больше, чем рекомендуют правила сложения, вычитания, умножения и деления приближенных чисел.
- При делении в результате следует сохранить столько значащих цифр, сколько их в приближенном данном с наименьшим числом верных значащих цифр. Поэтому
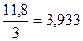 , т.к. в числе
, т.к. в числе 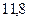 три значащих цифры (+ одна «запасная» цифра).
три значащих цифры (+ одна «запасная» цифра). - При вычитании приближенных чисел в результате следует сохранить столько десятичных знаков, сколько их в приближенном данном с наименьшим числом десятичных знаков. Поэтому
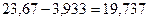 , т.к. наименьшее число десятичных знаков в числе 23,67 равно двум (+ одна «запасная» цифра).
, т.к. наименьшее число десятичных знаков в числе 23,67 равно двум (+ одна «запасная» цифра). - При возведении приближенного числа в квадрат в результате следует сохранить столько значащих цифр, сколько их в основании степени. Поэтому
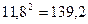 , т.к. в основании степени три значащих цифры (+ одна «запасная» цифра).
, т.к. в основании степени три значащих цифры (+ одна «запасная» цифра). - При умножении в результате следует сохранить столько значащих цифр, сколько их в приближенном данном с наименьшим числом верных значащих цифр. Поэтому
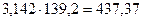 , т.к. в каждом числе четыре значащих цифры (+ одна «запасная» цифра).
, т.к. в каждом числе четыре значащих цифры (+ одна «запасная» цифра). - В окончательном результате «запасная» цифра отбрасывается. И т.к. меньшее число значащих цифр сомножителей равно трем (в числе 11,8), то в результате оставляем три значащих цифры.
Лабораторная работа №3 «Метод половинного деления»
- Отделить корни уравнения аналитически и уточнить один из них методом половинного деления с точностью до 0,01.
- Отделить корни уравнения графически и уточнить один из них методом половинного деления с точностью до 0,01.
1. а) 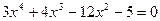 ; б)
; б) 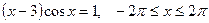 .
.
2. а) 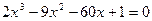 ; б)
; б) 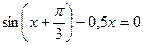 .
.
3. а) 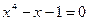 ; б)
; б) 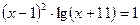 .
.
4. а) 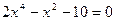 ; б)
; б) 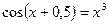 .
.
5. а) 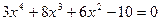 ; б)
; б) 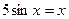 .
.
6. а) 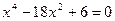 ; б)
; б) 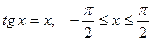 .
.
7. а) 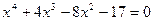 ; б)
; б) 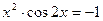 .
.
8. а) 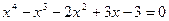 ; б)
; б) 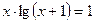 .
.
9. а) 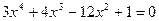 ; б)
; б) 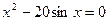 .
.
10. а) 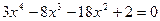 ; б)
; б) 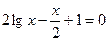 .
.
11. а) 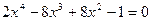 ; б)
; б) 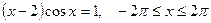 .
.
12. а) 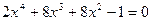 ; б)
; б) 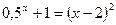 .
.
13. а) 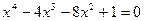 ; б)
; б) 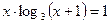 .
.
14. а) 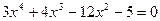 ; б)
; б) 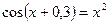 .
.
15. а) 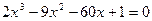 ; б)
; б) 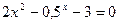 .
.
16. а) 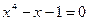 ; б)
; б) 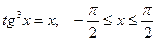 .
.
17. а) 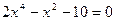 ; б)
; б) 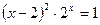 .
.
18. а) 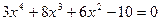 ; б)
; б) 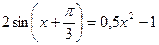 .
.
19. а) 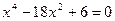 ; б)
; б) 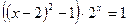 .
.
20. а) 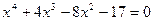 ; б)
; б) 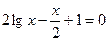 .
.
21. а) 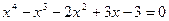 ; б)
; б) 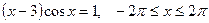 .
.
22. а) 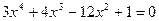 ; б)
; б) 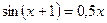 .
.
23. а) 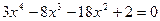 ; б)
; б) 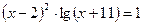 .
.
24. а) 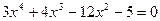 ; б)
; б) 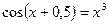 .
.
25. а) 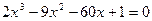 ; б)
; б) 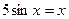 .
.
26. а) 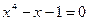 ; б)
; б) 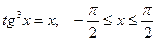 .
.
27. а) 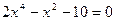 ; б)
; б) 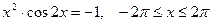 .
.
28. а) 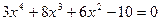 ; б)
; б) 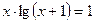 .
.
29. а) 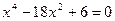 ; б)
; б) 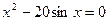 .
.
30. а) 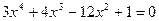 ; б)
; б) 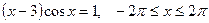 .
.
Пример 1. Отделить корни уравнения 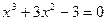 аналитически и уточнить меньший корень уравнения методом половинного деления с точностью до
аналитически и уточнить меньший корень уравнения методом половинного деления с точностью до 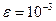 .
.
Решение.
а) Отделение корней.
Обозначим 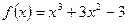 . Область определения функции
. Область определения функции 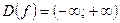 .
.
Находим производную 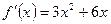 . Вычислим корни производной:
. Вычислим корни производной:
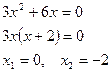
Составляем таблицу знаков функции 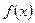 , полагая
, полагая 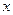 равным: а) критическим значениям функции (корням производной) или близким к ним; б) граничным значениям (исходя из области определения функции):
равным: а) критическим значениям функции (корням производной) или близким к ним; б) граничным значениям (исходя из области определения функции):
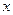
| 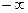
| -2 | 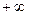
| |
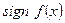
| - | + | - | + |
Т.к. происходят три перемены знака функции, то уравнение имеет три действительных корня. Чтобы завершить операцию отделения корней, следует уменьшить промежутки, содержащие корни, так чтобы их длина была не больше 1. Для этого составим новую таблицу знаков функции:
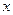
| 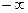
| -3 | -2 | -1 | 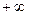
| ||
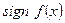
| - | - | + | - | - | + | + |
Отсюда видно, что корни уравнения находятся в следующих промежутках:
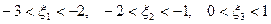 .
.
б) Уточняем меньший корень 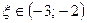 , применяя метод половинного деления. Все вычисления удобно производить, используя следующую таблицу:
, применяя метод половинного деления. Все вычисления удобно производить, используя следующую таблицу:
| 
| 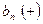
| 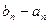
| 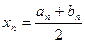
|  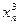
| 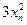
| 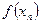
|
| -3 | -2 | -2,5000 | -15,6250 | 18,7500 | 0,1250 | ||
| -3 | -2,5000 | 0,5000 | -2,7500 | -20,7969 | 22,6875 | -1,1094 | |
| -2,7500 | -2,5000 | 0,2500 | -2,6250 | -18,0879 | 20,6719 | -0,4160 | |
| -2,6250 | -2,5000 | 0,1250 | -2,5625 | -16,8264 | 19,6992 | -0,1272 | |
| -2,5625 | -2,5000 | 0,0625 | -2,5313 | -16,2183 | 19,2217 | 0,0034 | |
| -2,5625 | -2,5313 | 0,0312 | -2,5469 | -16,5210 | 19,4601 | -0,0609 | |
| -2,5469 | -2,5313 | 0,0156 | -2,5391 | -16,3697 | 19,3411 | -0,0286 | |
| -2,5391 | -2,5313 | 0,0078 | -2,5352 | -16,2943 | 19,2817 | -0,0126 | |
| -2,5352 | -2,5313 | 0,0039 | -2,5333 | -16,2568 | 19,2521 | -0,0047 | |
| -2,5333 | -2,5313 | 0,0020 | -2,5323 | -16,2385 | 19,2376 | -0,0009 | |
| -2,5323 | -2,5313 | 0,0010 |
Т.к. 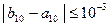 , то вычисления прекращаем.
, то вычисления прекращаем.
Тогда истинный корень уравнения 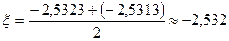 .
.
Пример 2. Отделить графически корень уравнения 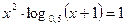 . Уточнить корень методом половинного деления с точностью до
. Уточнить корень методом половинного деления с точностью до 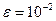 .
.
Решение.
Запишем уравнение в виде 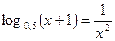 .
.
Построим графики функций 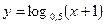 и
и 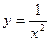 .
.
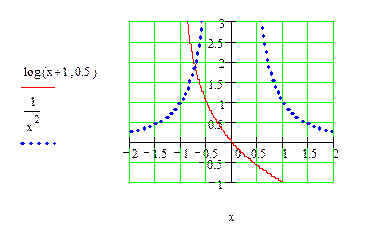
Из графика видно, что 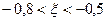 .
.
Для удобства расчетов перейдем к десятичным логарифмам:
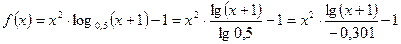 .
.
Далее вычисления производим в таблице:
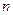
| 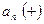
| 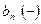
| 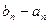
| 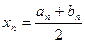
| 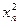
| 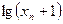
| 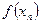
|
| -0,800 | -0,500 | 0,300 | -0,650 | 0,423 | -0,456 | -0,360 | |
| -0,800 | -0,650 | 0,150 | -0,725 | 0,526 | -0,561 | -0,021 | |
| -0,800 | -0,725 | 0,075 | -0,763 | 0,581 | -0,624 | 0,206 | |
| -0,763 | -0,725 | 0,038 | -0,744 | 0,554 | -0,592 | 0,088 | |
| -0,744 | -0,725 | 0,019 | -0,735 | 0,539 | -0,576 | 0,032 | |
| -0,735 | -0,725 | 0,010 |
Т.к. 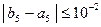 , то вычисления прекращаем.
, то вычисления прекращаем.
Тогда истинный корень уравнения 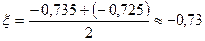 .
.
Лабораторная работа №4: «Решение нелинейных уравнений методом хорд и касательных».
1) Метод хорд.
1. Отделить корни уравнения графически и уточнить один из них методом хорд с точностью до 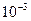 .
.
2. Отделить корни уравнения аналитически и уточнить один из них методом хорд с точностью до 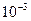 .
.
1. а) 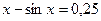 ; б)
; б) 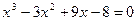 .
.
2. а) 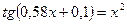 ; б)
; б) 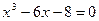 .
.
3. а) 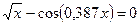 ; б)
; б) 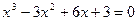 .
.
4. а) 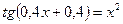 ; б)
; б) 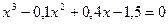 .
.
5 . а) 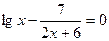 ; б)
; б) 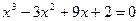 .
.
6. а) 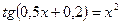 ; б)
; б) 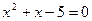 .
.
7. а) 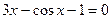 ; б)
; б) 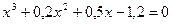 .
.
8. а) 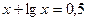 ; б)
; б) 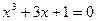 .
.
9. а) 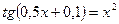 ; б)
; б) 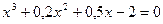 .
.
10. а) 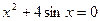 ; б)
; б) 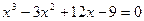 .
.
11. а) 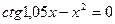 ; б)
; б) 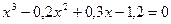 .
.
12. а) 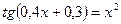 ; б)
; б) 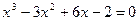 .
.
13. а) 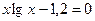 ; б)
; б) 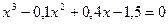 .
.
14. а) 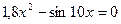 ; б)
; б) 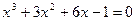 .
.
15. а) 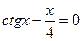 ; б)
; б) 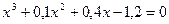 .
.
16. а) 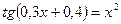 ; б)
; б) 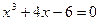 .
.
17. а) 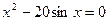 ; б)
; б) 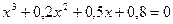 .
.
18. а) 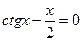 ; б)
; б) 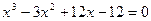 .
.
19. а) 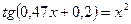 ; б)
; б) 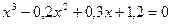 .
.
20. а) 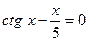 ; б)
; б) 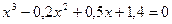 .
.
21. а) 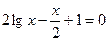 ; б)
; б) 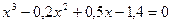 .
.
22. а) 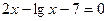 ; б)
; б) 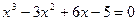 .
.
23. а) 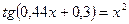 ; б)
; б) 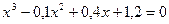 .
.
24. а) 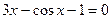 ; б)
; б) 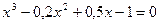 .
.
25. а) 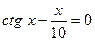 ; б)
; б) 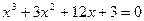 .
.
26. а) 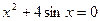 ; б)
; б) 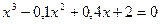 .
.
27. а) 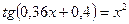 ; б)
; б) 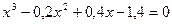 .
.
28. а) 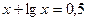 ; б)
; б) 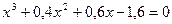 .
.
29. а) 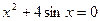 ; б)
; б) 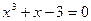 .
.
30. а) 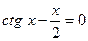 ; б)
; б) 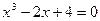 .
.
Образец выполнения задания.
1.Отделить корни графически уточнить один из них методом хорд до 0,001.
tg( 0,55x+0,1)=x2
Обозначим у1= tg( 0,55x+0,1) у2=x2
Составим таблицу значений:
| X | 0,2 | 0,4 | 0,6 | 0,8 | ||
| Y2=X2 | 0,04 | 0,16 | 0,36 | 0,64 | ||
| 0,55x+0,1 | 0,1 | 0,21 | 0,32 | 0,43 | 0,54 | 0,65 |
| Y1 | 0,100335 | 0,213142 | 0,331389 | 0,458621 | 0,59943 | 0,760204 |
Построим график:
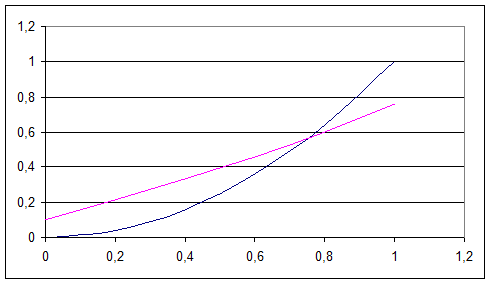
Видим, что хÎ[0,6;0,8].
Чтобы уточнить его методом хорд, определим знаки функции на концах отрезка
[0,6;0,8] и знак её второй производной в этом промежутке:
f(0,6)=tg0,43-0,36=0,0986
f(0,8)=tg0,54-0,64=-0,0406
f’(x)=0,55/(cos2(0,55x+0,1))-2x
f’’(x)=0,55×2cos-3(0,55x+0,1)×sin(0,55x+0,1)×0,55-2<0 при хÎ[0,6;0,8].
f’’(x)× f(0,8)>0, значит х0=0,6
Для вычислений используем формулу:
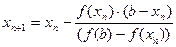 , где b=0,8, x0=0,6.
, где b=0,8, x0=0,6.
Вычисления производим в таблице:
| n | xn | 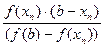
|
| 0,60000 | -0,14168 | |
| 0,74168 | -0,0081 | |
| 0,74978 | -0,00039 | |
| 0,75017 | -1,9E-05 | |
| 0,75019 | -8,9E-07 |
Ответ: х»0,750.
2. Отделить корни аналитически и уточнить один из них методом хорд до 0,001.
f(x)=x3-0,2x2+0,5x+1,5
f’(x)=3x2-0,4x+0,5 D=0,16-6<0
Составим таблицу знаков f(x):
| x | -
| -1 | +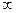
| |
| Sign f(x) | - | - | + | + |
Получаем один действительный корень в промежутке [-1; 0].
Чтобы уточнить его, найдём 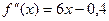 , в промежутке [-1; 0]
, в промежутке [-1; 0] 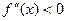 ,
,
f’’(a)× f(х)>0, значит х0=b=0.
Вычисления произведём по формуле:
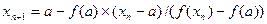 ,
,
где a=-1, х0=b=0, f(a)= f(-1)-1-0,2-0,5+1,5=-0,2.
Вычисления производим в виде таблицы:
| n | xn | xn3 | xn2 | 0,2xn2 | 0,5xn | f(xn) | f(xn)+0,2 | xn-a | h |
| 1,5 | 1,7 | -0,11765 | |||||||
| -0,88235 | -0,68695 | 0,77855 | 0,15571 | -0,44118 | 0,21616 | 0,41616 | 0,11765 | -0,05654 | |
| -0,94346 | -0,83979 | 0,89012 | 0,17802 | -0,47173 | 0,01045 | 0,21045 | 0,05654 | -0,05373 | |
| -0,94627 | -0,84731 | 0,89543 | 0,17909 | -0,47313 | 0,00047 | 0,20047 | 0,05373 | -0,05361 | |
| -0,94639 |
Ответ: х»-0,946
Метод касательных (Ньютона).
Где x0=a, если f(a)×f’’(x)>0; x0=b, если f(b)×f’’(x)>0 на [a;b].
Так как f(0,6)>0,f(0,8)<0, f’’(x)<0, то за начальное приближение берём х0=0,8. Вычисления производим по формуле: f’(0,8)=0,55/(cos2(0,55x+0,1))-2x=-0,8523. Вычисления производим в виде таблицы: n xn f’(x)=0,55/(cos2(0,55x+0,1))-2x …Решение нелинейных уравнений методом простой итерации».
2) Отделить корни уравнения аналитически и уточнить один из них методом итераций с точностью до 0,001. Пример выполнения задания: 1) 2x+lg(2x+3)=1 Найдём приближённые значения корней графически:Метод главных элементов для решения системы уравнений
a11x1 + a12x2 + a13x3 = a14 a21x1 + a22x2 + a23x3 = a24 a31x1 + a32x2 + a33x3 = a34Схема Халецкого
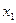
| 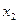
| 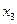
| 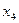
| Свободные члены | |
| I | 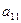
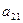
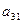
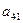
| 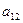
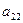
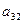
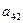
| 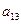
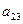
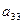
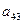
| 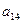
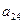
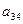
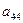
| 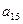
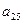
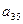
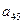
|
| II | 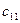
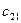
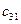
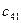
| 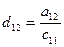
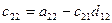
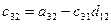
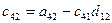
| 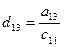
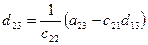
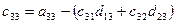
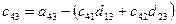
| 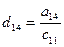
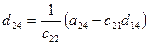
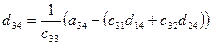
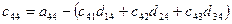
| |
| III | 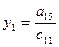
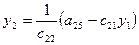
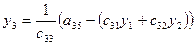
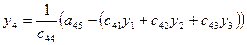
|
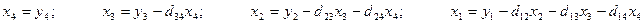
Схема Халецкого для решения системы уравнений (в общем виде)
| Хi1 | Хi2 | Xi3 | Xi4 | Свободные члены | Контрольные суммы |
| a11 | a12 | a13 | a14 | a15 | 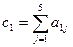
|
| a21 | a22 | a23 | a24 | a25 | 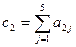
|
| a31 | a32 | a33 | a34 | a35 | 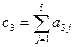
|
| a41 | a42 | a43 | a44 | a45 | 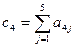
|
| b11 | α12 | α 13 | α 14 | α15 | β1 |
| b21 | b22 | α 23 | α 24 | α25 | β2 |
| b31 | b32 | b33 | α 34 | α35 | β3 |
| b41 | b42 | b43 | b44 | α45 | β4 |
| x4 | 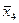
| ||||
| x3 | 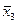
| ||||
| x2 | 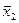
| ||||
| x1 | 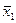
|
Вычислительные формулы:
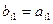 (i=1,2,3,4)
(i=1,2,3,4)
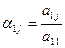 (j=2,3,4,5),
(j=2,3,4,5), 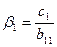 ,
, 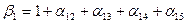
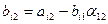 (i=2,3,4)
(i=2,3,4)
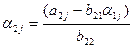 (j=3,4,5),
(j=3,4,5), 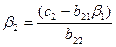 ,
, 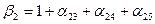
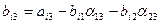 (i=3,4)
(i=3,4)
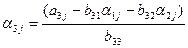 (j=4,5),
(j=4,5), 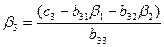 ,
, 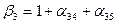
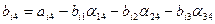 (i=4)
(i=4)
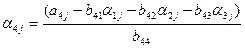 (j=5),
(j=5), 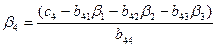 ,
, 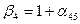
Значения переменных вычисляются по схеме единственного деления:
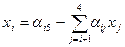 ,
, 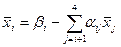 , проверка
, проверка 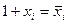 (i=4,3,2,1)
(i=4,3,2,1)
Порядок заполнения таблицы:
- В первый раздел таблицы вписываем матрицу коэффициентов и свободные члены.
- Элементы столбца
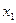 из раздела I переносим в столбец
из раздела I переносим в столбец 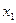 раздела II, т.к.
раздела II, т.к. 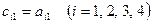 .
. - Вычисляем элементы первой строки раздела II. Для этого делим все элементы первой строки раздела I на элемент
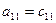 .
. - Заполняем столбец
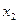 раздела II, начиная со второй строки. Находим
раздела II, начиная со второй строки. Находим 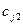 .
. - Заполняем вторую строку раздела II, определяя
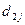 .
. - Заполняем столбец
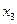 , вычисляя элементы
, вычисляя элементы 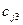 .
. - Заполняем третью строку раздела II, определяя
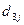 .
. - Находим
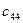 . 9.Определяем
. 9.Определяем 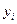 . 10.Находим
. 10.Находим 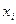 .
.
Лабораторная работа №10 «Метод квадратных корней»
Решить систему линейных уравнений методом квадратных корней с точностью до 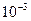 .
.
1. 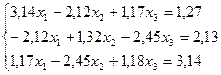 16.
16. 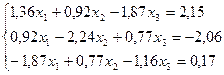
2. 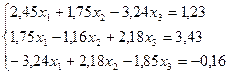 17.
17. 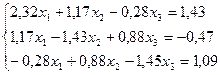
3. 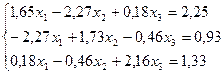 18.
18. 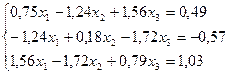
4. 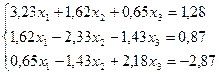 19.
19. 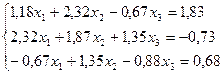
5. 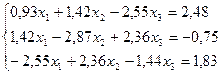 20.
20. 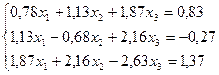
6. 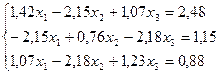 21.
21. 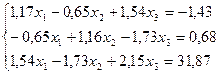
7. 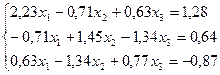 22.
22. 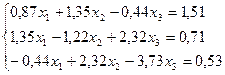
8. 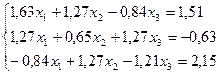 23.
23. 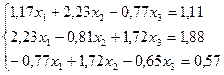
9. 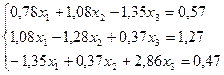 24.
24. 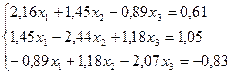
10. 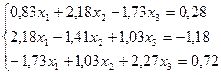 25.
25. 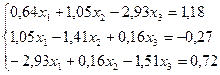
11. 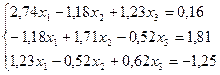 26.
26. 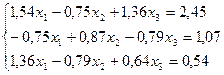
12. 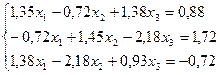 27.
27. 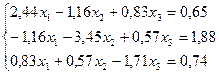
13. 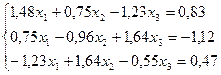 28.
28. 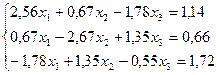
14. 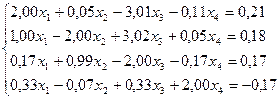 29.
29. 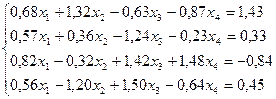
15. 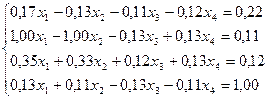 30.
30. 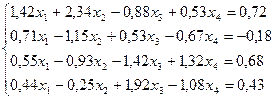
Схема метода квадратных корней
| I | 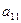
| 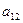
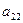
| 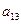
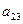
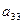
| 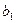
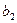
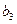
|
| II | 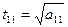
| 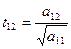
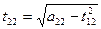
| 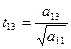
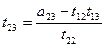
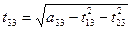
| 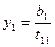
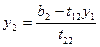
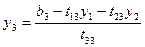
|
| III | 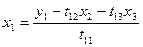
| 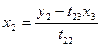
| 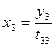
|
Порядок заполнения таблицы:
1. В первый раздел таблицы записываем коэффициенты системы.
2. Находим 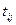 и записываем результаты во второй раздел таблицы.
и записываем результаты во второй раздел таблицы.
3. Находим 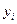 и записываем результаты во второй раздел таблицы.
и записываем результаты во второй раздел таблицы.
4. Находим 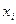 и записываем результаты в третий раздел таблицы (находим последовательно находим ваем результаты в третий раздел таблицы.
и записываем результаты в третий раздел таблицы (находим последовательно находим ваем результаты в третий раздел таблицы.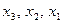 ).
).
Замечание.При действительных 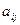 могут получиться чисто мнимые
могут получиться чисто мнимые 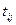 . Метод применим и в этом случае.
. Метод применим и в этом случае.
Лабораторная работа №11 «Метод итераций»
Методом итераций решить систему линейных уравнений с точностью до 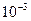 , предварительно оценив число необходимых для этого шагов.
, предварительно оценив число необходимых для этого шагов.
1. 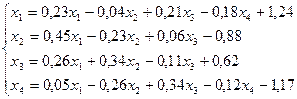
2. 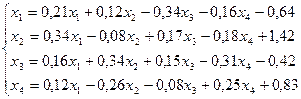
3. 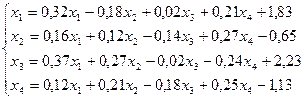
4. 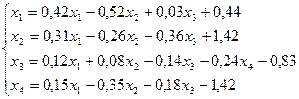
5. 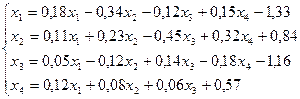
6. 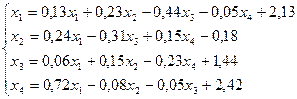
7. 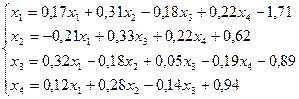
8. 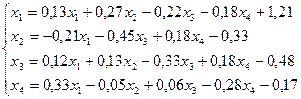
9. 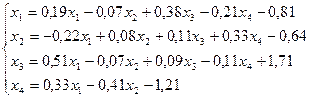
10. 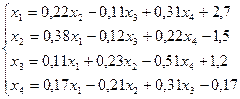
11. 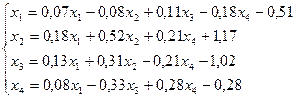
12. 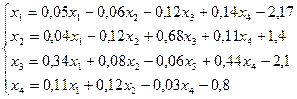
13. 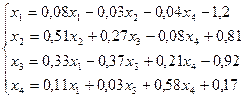
14. 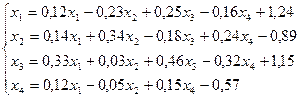
15. 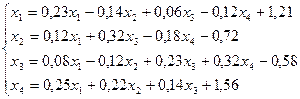
16. 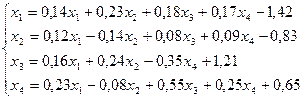
17. 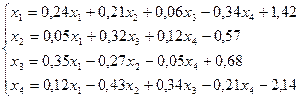
18. 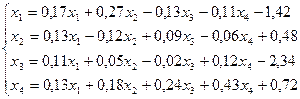
19. 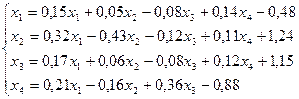
20. 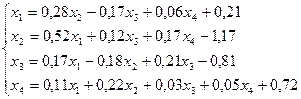
21. 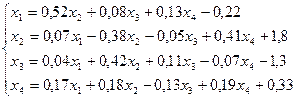
22. 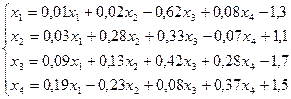
23. 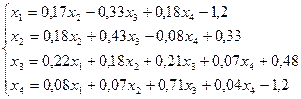
24. 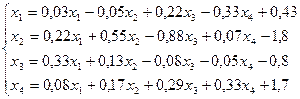
25. 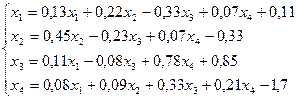
26. 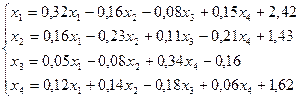
27. 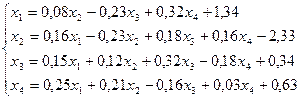
28. 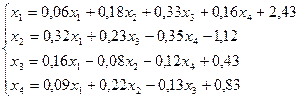
29. 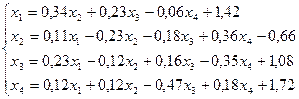
30. 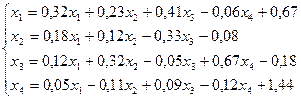
Пример. Решить систему линейных уравнений с точностью до 0,01 методом итераций, предварительно определив необходимое количество шагов:
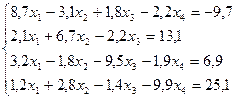
Решение.
Приведем систему к нормальному виду 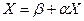 :
:
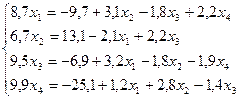
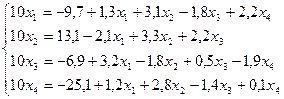
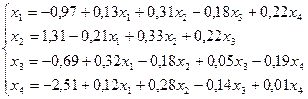
Определим число итераций, используя формулу 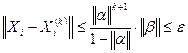 , где
, где 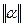 - одна из трех норм матрицы
- одна из трех норм матрицы 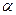 ,
, 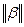 - та же норма вектора
- та же норма вектора 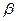 ,
, 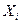 - вектор точных значений неизвестных линейной системы,
- вектор точных значений неизвестных линейной системы, 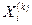 -
- 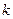 -е приближение значений неизвестных, вычисленное методом итераций,
-е приближение значений неизвестных, вычисленное методом итераций, 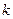 - число итераций, необходимое для достижения заданной точности.
- число итераций, необходимое для достижения заданной точности.
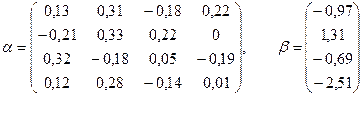
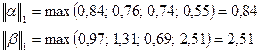
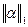 - норма 1 – максимальная сумма модулей элементов матрицы по строкам;
- норма 1 – максимальная сумма модулей элементов матрицы по строкам;
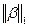 - максимальная из координат вектора, взятая по модулю.
- максимальная из координат вектора, взятая по модулю.
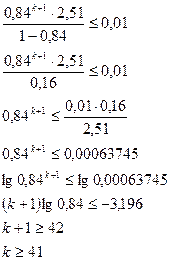
Последовательные приближения находим по формуле 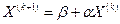 . За нулевые приближения берем свободные члены.
. За нулевые приближения берем свободные члены.
Вычисления располагаем в таблице:
| 
| 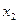
| 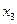
| 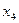
|
| -0,97 | 1,31 | -0,69 | -2,51 | |
| -1,118 | 1,794 | -0,794 | -2,188 | |
| -0,898 | 1,962 | -0,995 | -2,053 | |
| -0,751 | 1,927 | -0,990 | -1,950 | |
| -0,721 | 1,886 | -0,956 | -1,941 | |
| -0,734 | 1,873 | -0,939 | -1,954 | |
| -0,746 | 1,876 | -0,938 | -1,962 | |
| -0,748 | 1,879 | -0,940 | -1,963 |
Т.к. 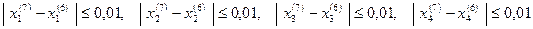 , вычисления заканчиваем.
, вычисления заканчиваем.
Округляя последние приближения, получаем ответ.
Ответ: 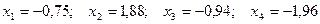 .
.
Лабораторная работа № 12 «Метод Зейделя»
Методом Зейделя решить систему линейных уравнений с точностью до 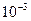 (использовать задание из работы №10).
(использовать задание из работы №10).
Пример. Решить систему линейных уравнений с точностью до 0,01 методом Зейделя:
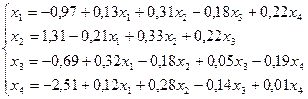
Решение.
За нулевые приближения возьмем свободные члены и подставим в первое уравнение системы: 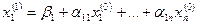 .
.
Полученное первое приближение 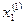 подставляем во второе уравнение системы:
подставляем во второе уравнение системы: 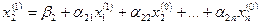 .
.
Полученные первые приближения 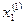 и
и 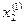 подставляем в третье уравнение системы:
подставляем в третье уравнение системы: 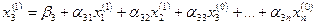
И т.д.
Вычисления располагаем в таблице:
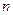
| 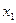
| 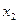
| 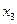
| 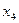
|
| -0,97 | 1,31 | -0,69 | -2,51 | |
| -1,118 | 1,825 | -0,934 | -2,027 | |
| -0,827 | 1,881 | -0,955 | -1,969 | |
| -0,756 | 1,879 | -0,944 | -1,962 | |
| -0,747 | 1,880 | -0,942 | -1,961 |
Т.к. 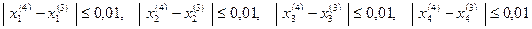 , вычисления заканчиваем.
, вычисления заканчиваем.
Округляя последние приближения, получаем ответ.
Ответ: 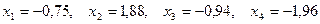
Лабораторная работа13.
Интерполирование функции многочленом Лагранжа.
Функция f(x)= определена на отрезке [1; 1,2]. Интерполировать функцию многочленом Лагранжа и найти значение функции в точке x=1,13. Дать оценку… а) по формуле для неравноотстоящих узлов. б) по формуле для равноотстоящих узлов. xi 1,02 1,04 1,06 1,08 …Лабораторная работа14.
Интерполирование функции многочленом Ньютона.
Даны значения функции f(x)= на отрезке [1; 1,2]. а) Интерполировать функцию многочленом Ньютона (первая интерполяционная… б) Интерполировать функцию многочленом Ньютона (вторая интерполяционная формула) и найти значение функции в точке…Лабораторная работа15.
Сплайновая интерполяция.
x 0,5 f(x) 1,5 … Решение: а) Осуществим кусочно-линейное интерполирование. Для этого разобьем данную функцию на отрезки, определяемые соседними…Лабораторная работа16
Интерполяция функции кубическим сплайном. Метод прогонки.
Задание:
- На отрезке [1;1,2] построить кубический сплайн шагом h = 0,04, удовлетворяющий на концах отрезка краевым условиям I типа и интерполирующий функцию
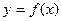 . Найти значение сплайна в точках: 1,05; 1,09; 1,13; 1,15; 1,17.
. Найти значение сплайна в точках: 1,05; 1,09; 1,13; 1,15; 1,17. - Решить систему методом прогонки.
Вариант №1
1. 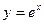
2. 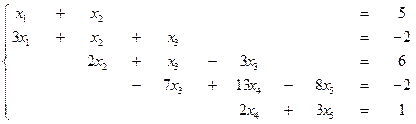
Вариант №2
1. 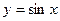
2. 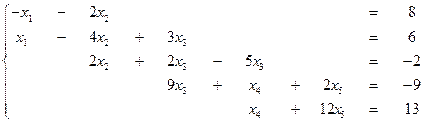
Вариант №3
1. 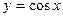
2. 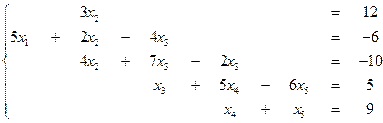
Вариант №4
1. 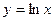
2. 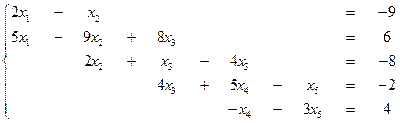
Вариант №5
1. 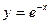
2. 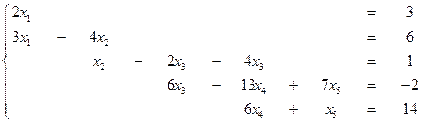
Образец выполнения задания:
1. На отрезке 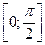 построить кубический сплайн шагом
построить кубический сплайн шагом 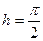 , удовлетворяющий на концах отрезка краевым условиям I типа и интерполирующий функцию
, удовлетворяющий на концах отрезка краевым условиям I типа и интерполирующий функцию 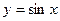 . С помощью интерполяционной формулы вычислить приближенное значение
. С помощью интерполяционной формулы вычислить приближенное значение 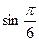 .
.
Решение:
Будем искать кубическую параболу 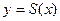 ,удовлетворяющую следующим условиям на концах отрезка
,удовлетворяющую следующим условиям на концах отрезка 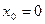 и
и 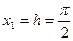 :
:
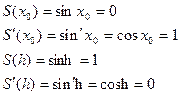
Воспользуемся формулой:
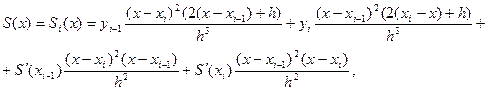
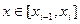 ,
, 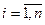 .
.
Получим:
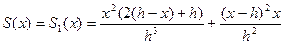 (
(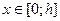 )
)
Преобразуем:
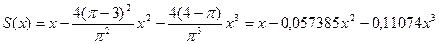 .
.
Тогда 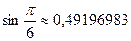 .
.
2. Решить систему методом прогонки.
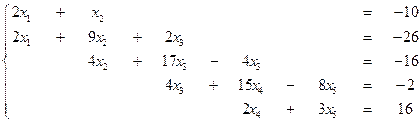
Решение:
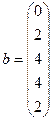 ;
; 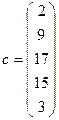 ;
;  ;
; 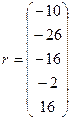
Воспользуемся формулами:
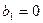 :
: 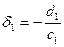 ;
; 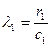
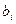 :
: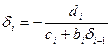 ;
; 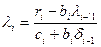
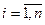
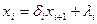 (
(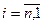 )
)
| i | bi | ci | di | ri | δi | λi | xi |
| -10 | -0,5 | -5 | -4 | ||||
| -26 | -0,25 | -2 | -2 | ||||
| -4 | -16 | 0,25 | -0,5 | ||||
| -8 | -2 | 0,5 | |||||
Ответ: 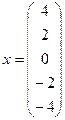 .
.
Лабораторная работа17
Среднеквадратическое приближение
Задание: Установить вид эмпирической формулы 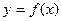 , используя аппроксимирующую зависимость с тремя параметрами a, b и c, имеющую вид
, используя аппроксимирующую зависимость с тремя параметрами a, b и c, имеющую вид 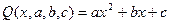 . Опытные данные определены таблицей.
. Опытные данные определены таблицей.
Вариант №1
| xi | ||||
| yi |
Вариант №2
| xi | ||||
| yi |
Вариант №3
| xi | ||||
| yi |
Вариант №4
| xi | ||||
| yi |
Вариант №5
| xi | ||||
| yi |
Вариант №6
| xi | ||||
| yi |
Вариант №7
| xi | ||||
| yi |
Образец выполнения задания:
| xi | ||||
| yi |
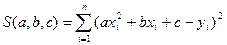
Для нахождения a, b и c составим систему уравнений вида:
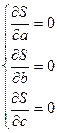
Отсюда получаем систему трех линейных уравнений с тремя неизвестными:
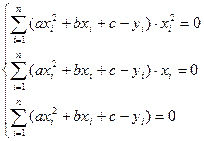
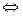
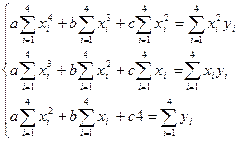
| xi | yi | xi2 | xi3 | xi4 | xiyi | xi2yi |
| Сумма |
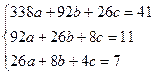
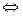
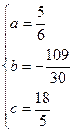
Эмпирическая формула представляет собой функцию:
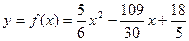 .
.
Лабораторная работа18
Ортогональные многочлены Чебышева
Вариант №1
1. 
|
Вариант №2
1. 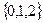
|
Вариант №3
1. 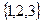
|
Вариант №4
1. 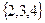
|
Вариант №5
1. 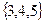
|
Вариант №6
1. 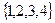
|
Образец выполнения задания:
1. 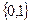
Многочленами Чебышева на множестве точек 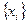 (
(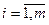 ) называются алгебраические многочлены, ортогональные на этом множестве, с нормой
) называются алгебраические многочлены, ортогональные на этом множестве, с нормой 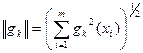 (
(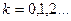 ) , отличной от нуля, и определяемые следующими рекуррентными формулами:
) , отличной от нуля, и определяемые следующими рекуррентными формулами:
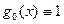
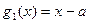
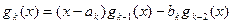 (
(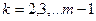 )
)
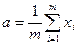 (
(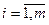 )
)
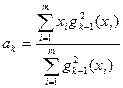
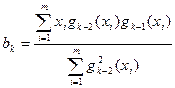
В данном примере  . Имеем
. Имеем
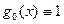 ;
; 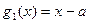 ;
; 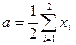
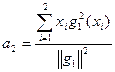 ;
; 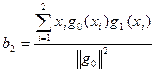
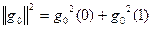
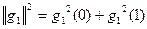
| i | xi | a | g0(xi) | g02(xi) | g1(xi) | g12(xi) | xig12(xi) | xig0(xi)g1(xi) | a2 | b2 |
| -0,5 | 0,25 | |||||||||
| 0,5 | 0,25 | 0,25 | 0,5 | |||||||
| Сумма | 0,5 | 0,25 | 0,5 | |||||||
| 0,5 | 0,5 | 0,25 |
Далее, используя рекуррентные соотношения, построим функцию
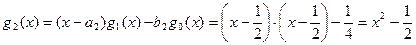 .
.
| i | xi | g2(xi) |
| -0,5 | ||
| 0,5 | ||
| Сумма |
Норма функции 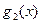 на множестве
на множестве 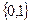 не равна нулю и, следовательно, эта функция является многочленом Чебышева.
не равна нулю и, следовательно, эта функция является многочленом Чебышева.
2.
| i | ||||
| xi | ||||
| yi |
Составим ортогональные многочлены Чебышева 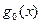 ,
,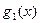 ,
, 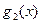 ,
, 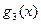 на множестве точек
на множестве точек 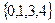 . Имеем
. Имеем
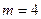
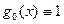 ;
; 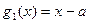 ;
; 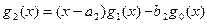 ;
; 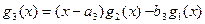
| i | xi | a | g02(xi) | g12(xi) | g22(xi) | g32(xi) | a2 | b2 | a3 | b3 |
| 2,25 | 1,44 | |||||||||
| 2,25 | 5,76 | |||||||||
| 2,25 | 5,76 | |||||||||
| 2,25 | 1,44 | |||||||||
| Сумма | 14,4 | |||||||||
| 2,5 | 0,9 |
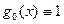 ;
; 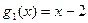 ;
; 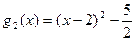 ;
; 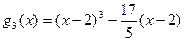
| i | xi | g0(xi) | g1(xi) | g2(xi) | g3(xi) |
| -2 | 1,5 | -1,2 | |||
| -1 | -1,5 | 2,4 | |||
| -1,5 | -2,4 | ||||
| 1,5 | 1,2 |
Многочлены наилучшего приближения имеют вид:
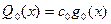 ,
, 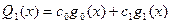 ,
, 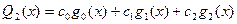 ,
, 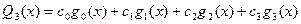 .
.
Здесь коэффициенты Фурье определены по формуле:
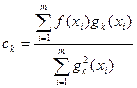 (
(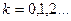 )
)
| i | xi | g0(xi) | g1(xi) | g2(xi) | g3(xi) | xig0(xi) | xig1(xi) | xig2(xi) | xig3(xi) | c0 | c1 | c2 | c3 |
| -2 | 1,5 | -1,2 | -8 | -4,8 | |||||||||
| -1 | -1,5 | 2,4 | |||||||||||
| -1,5 | -2,4 | -1,5 | -2,4 | ||||||||||
| 1,5 | 1,2 | 2,4 | |||||||||||
| Сумма | -3 | 7,5 | -4,8 | ||||||||||
| 1,75 | -0,3 | 0,833 | -0,33 |
Квадрат наименьшего среднеквадратического отклонения:
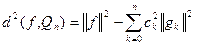
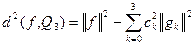
| i | yi | yi2 | c02 | c12 | c22 | c32 |
| Сумма | ||||||
| 3,063 | 0,09 | 0,69 | 0,111 |
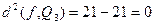
Тем самым найдены алгебраические многочлены наименьшего среднеквадратического приближения 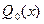 ,
, 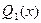 ,
, 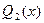 ,
, 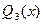 :
:
| i | xi | g0(xi) | g1(xi) | g2(xi) | g3(xi) | c0 | c1 | c2 | c3 | Q0 | Q1 | Q2 | Q3 |
| -2 | 1,5 | -1,2 | 1,75 | 2,35 | 3,6 | ||||||||
| -1 | -1,5 | 2,4 | 1,75 | 2,05 | 0,8 | ||||||||
| -1,5 | -2,4 | 1,75 | 1,45 | 0,2 | |||||||||
| 1,5 | 1,2 | 1,75 | 1,15 | 2,4 | |||||||||
| Сумма | |||||||||||||
| 1,75 | -0,3 | 0,833 | -0,33 |
Отметим, что 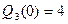 ,
, 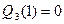 ,
, 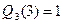 ,
, 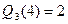 .
.
Лабораторная работа19.
Вычисление определенных интегралов по формуле трапеций и формуле Симпсона, по формуле левых, правых и средних прямоугольников.
1. Вычислить интеграл по формуле трапеций с тремя десятичными знаками. Решение: Для достижения заданной степени точности необходимо определить значение n max,Таблица 2.
| i | xi | 2xi-2,l | sin (2xi-2,1) | xi2+1 | y0,y8 | y1, y3, y5, y7 | y2, y4, y6 |
| 0 | 1,20 | 0,30 | 0,29552 | 2,44 | 0,1211 | ||
| 1 | 1,25 | 0,40 | 0,38942 | 2,5625 | 0,1520 | ||
| 2 | 1,30 | 0,50 | 0,4794 | 2,69 | 0,1782 | ||
| 3 | 1,35 | 0,60 | 0,5646 | 2,8225 | 0,2000 | ||
| 4 | 1,40 | 0,70 | 0,6442 | 2,96 | 0,2176 | ||
| 5 | 1,45 | 0,80 | 0,7174 | 3,1024 | 0,2312 | ||
| 6 | 1,50 | 0,90 | 0,7833 | 3,25 | 0,2410 | ||
| 7 | 1,55 | 1,00 | 0,8415 | 3,4025 | 0,2473 | ||
| 8 | 1,60 | 1,10 | 0.8912 | 3,56 | 0,2503 | ||
| S | 0,3713 | 0,8305 | 0,6368 |
Следовательно, I» 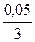 (0,3714+4 •0,8305+2 • 0,6368) »0,88278.Для оценки точности полученного результата составим таблицу конечных разностей функций до разностей четвертого порядка (табл. 3).
(0,3714+4 •0,8305+2 • 0,6368) »0,88278.Для оценки точности полученного результата составим таблицу конечных разностей функций до разностей четвертого порядка (табл. 3).
Так как max |D4yi|=0,0001, то остаточный член формулы
Rост<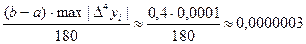
Вычисления производились с четырьмя значащими цифрами, а потому величина остаточного члена на погрешность не влияет.
Погрешность вычислений можно оценить из соотношения
DI = (b -a) •Dу < 0,4 • 0,0001 < 0,00005. Значит, полученные четыре десятичных знака верны.
Таблица 3.
| I | уi | Dyi | D2yi | D3yi | D4yi |
| 0 | 0,1211 | 0,0309 | -0,0047 | 0,0003 | -0,0001 |
| 1 | 0,1520 | 0,0262 | -0,0044 | 0,0002 | 0.0000 |
| 2 | 0,1782 | 0,0218 | -0,0042 | 0,0002 | 0.0000 |
| 3 | 0,2000 | 0,0176 | -0,0040 | 0,0002 | 0,0001 |
| 4 | 0,2176 | 0,0136 | -0,0038 | 0,0003 | -0,0001 |
| 5 | 0,2312 | 0.0098 | -0,0035 | 0,0002 | |
| 6 | 0,2410 | 0,0063 | -0,0033 | ||
| 7 | 0,2473 | 0,0030 | |||
| 8 | 0,2503 |
Самостоятельно:
1) 
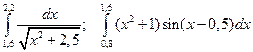
2)
3)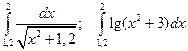
4)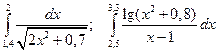
Вычислить определенный интеграл по формуле левых и правых прямоугольников.
Для вычисления по формулам левых, правых и средних прямоугольников при n=10… В таблице найдены суммы:Вычислить определенный интеграл по формуле средних прямоугольников.
Для решения воспользуемся формулой средних прямоугольников: Вычисления производим с шагом h=(b-a)/10=(1,2-0,4)/10=0,08. i … Приближённое значение интеграла:Лабораторная работа 20.
Метод Эйлера с уточнением
Образец выполнения: y¢=x+sin(y/2,25); y0(1,4)=2,2, xÎ[1,4;2,4] Метод Эйлера с уточнением заключается в том, что каждое значение yk+1=y(xk+1), где y(x) — искомая функция, а…Л/р 21«Численное решение ДУ первого порядка методом Рунге-Кутты 4-го порядка».
1) , , , 2) , , , 3) , , ,Л/р22 «Решение ДУ первого порядка методом Адамса-Башфорта».
1) , , , 2) , , , 3) , , ,Лабораторная работа23
Решение краевой задачи для обыкновенного дифференциального уравнения методом конечных разностей
Задание: Используя метод конечных разностей, составить решение краевой задачи для обыкновенного дифференциального уравнения с точностью
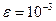 ; шаг
; шаг 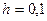 ;
;
Вариант №1
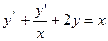 ;
; 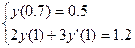 ;
;
Вариант №2
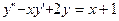 ;
; 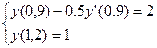 ;
;
Вариант №3
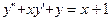 ;
; 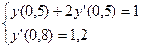 ;
;
Вариант №4
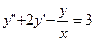 ;
; 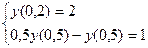 ;
;
Образец выполнения задания:
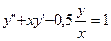 ;
; 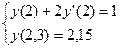 ;
;
Разбив отрезок 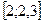 на части с шагом
на части с шагом 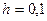 , получим четыре узловые точки с абсциссами:
, получим четыре узловые точки с абсциссами: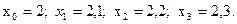 . Две точки являются конечными, а две другие внутренними. Данное уравнение во внутренних точках замени конечно-разностным уравнением:
. Две точки являются конечными, а две другие внутренними. Данное уравнение во внутренних точках замени конечно-разностным уравнением:
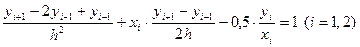 .
.
Из краевых условий составим конечно-разностные уравнения в конечных точках:
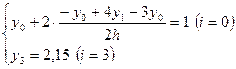
Данная задача сводится к решению системы уравнений:
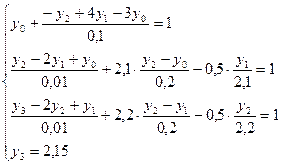
Выполнив преобразования, имеем:
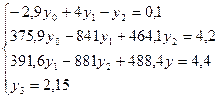
Поставив значение 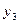 в третье уравнение, получим для определения остальных неизвестных систему:
в третье уравнение, получим для определения остальных неизвестных систему:
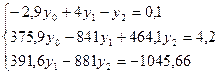

Для решения полученной системы воспользуемся, например, схемой «главных элементов».
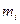
| 
| 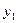
| 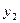
| Свободные члены | S |
| -0,00113507 -1 | -2,9 375,9 | -841 391,6 | -1 464,1 -881 | 0,1 4,2 -1045,66 | 0,2 3,2 -1535,06 |
| 0,00560179 -1 | -2,9 375,9 | 3,55551 -643,7098 | - - | 1,28690 -546,6411 | 1,94240 -805,4511 |
| -1 | -0,79429 | - | - | -1,77527 | -2,56957 |
| 2,2350 3,2351 | 2,1849 3,1849 | 2,1580 3,1580 |
Ответ:
| x | y | x | y |
| 2.0 2.1 | 2.235 2.185 | 2.2 2.3 | 2.185 2.150 |
Лабораторная работа 24
«Численные методы поиска минимума функции нескольких переменных»
1.Минимизировать функцию в Е^2 методом градиентного спуска с дроблением шага (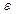 =0,05)
=0,05)
1)f(x,y)=2x+y+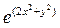
2) f(x,y)=1.5x+1.1y+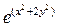
3) f(x,y)=0.5x+2y+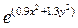
4) f(x,y)=1.8x+0.4y+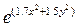
5) f(x,y)=3x+2y+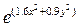
Пример: 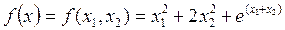
Следим, чтобы выполнялось условие монотонности 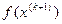 <
<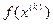
и вычисляем, пока не будет выполняться условие 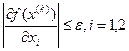
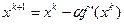
В качестве начального приближения 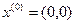 и
и 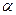 =1.
=1.
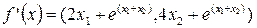
k=0; 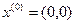 ;
; 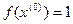 ;
; 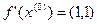 ;
; 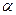 =1;
=1;
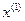 =
=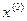 -
-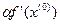 =(0, 0) – (1, 1) =(-1 , -1)
=(0, 0) – (1, 1) =(-1 , -1)
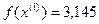 >
> 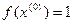 - условие монотонности нарушено
- условие монотонности нарушено
Уменьшаем 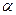 в 2 раза
в 2 раза 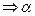 =0.5
=0.5
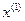 =
=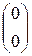 – 0,5
– 0,5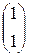 =
=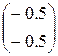
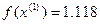 >
> 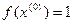 - условие монотонности нарушено
- условие монотонности нарушено
Уменьшаем 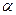 в 2 раза
в 2 раза 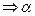 =0.25
=0.25
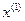 =(0, 0) –0.25 (1,1)=(-0,25,-0,25)
=(0, 0) –0.25 (1,1)=(-0,25,-0,25)
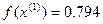 <
< 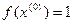 - условие монотонности выполняется
- условие монотонности выполняется
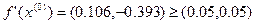
Условие останова не выполнено.
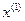 =(-0,25,-0,25),
=(-0,25,-0,25), 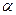 =0,25
=0,25
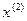 =(-0,25,-0,25)-0,25
=(-0,25,-0,25)-0,25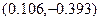 =(-0,277,-0,152)
=(-0,277,-0,152)
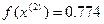 <
< 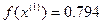 - условие монотонности выполняется
- условие монотонности выполняется
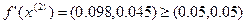
Условие останова не выполнено.
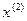 =(-0,277,-0,152)
=(-0,277,-0,152)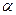 =0,25
=0,25
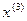 =(-0,277,-0,152)-0.25
=(-0,277,-0,152)-0.25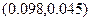 =(-0.301,-0.162)
=(-0.301,-0.162)
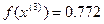 <
< 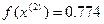 - условие монотонности выполняется
- условие монотонности выполняется
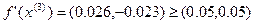
Условие останова выполнено.
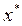 =(-0.301,-0.162) ,
=(-0.301,-0.162) , 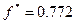
2.Минимизировать квадратичную функцию в Е^2 методом наискорейшего спуска(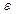 =0,01):
=0,01):
Квадратичная функция имеет вид: f(x)=1/2(Ax,x)-(b,x);
A-симметричная, положительно определенная матрица n*n, x 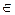 Е^2,b
Е^2,b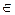 Е^2.
Е^2.
Ax=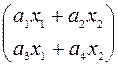 ; (Ax,x)=
; (Ax,x)= 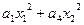 +
+ ;
;
(b,x)= 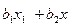
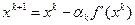
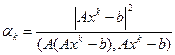
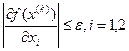
Для случая Е^2 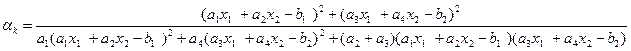
Пример:
В качестве начального приближения 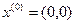
A=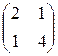 ; b=
; b=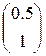 то
то 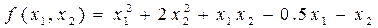
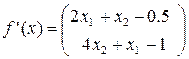
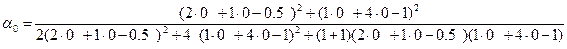 =0,227273
=0,227273
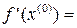
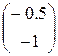
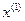 =
=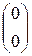 – 0,227273
– 0,227273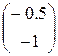 =
=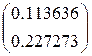
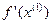 =
=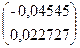
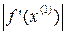
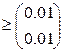
Условие останова не выполнено
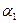 =0.625
=0.625
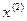 =
=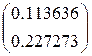 – 0.625
– 0.625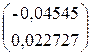 =
=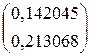
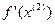 =
=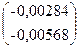
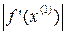
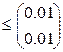
Условие останова выполнено.
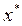 =
= 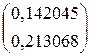 ,
, 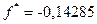
1) A=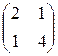 ; b=
; b=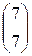
2 )A= ; b=
; b=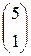
3 )A=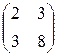 ; b=
; b=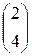
4 )A=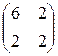 ; b=
; b=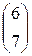
5) A=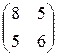 ; b=
; b=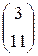
3. Минимизировать квадратичную функцию в Е^2 методом сопряжённых градиентов:
Примеры:
1. 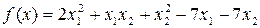
2. 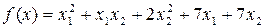
3. 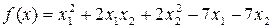
4. 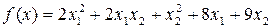
5. 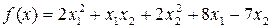
Квадратичная функция имеет вид: f(x)=1/2(Ax,x)-(b,x);
A-симметричная, положительно определенная матрица n*n, x 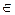 Е^2,b
Е^2,b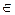 Е^2.
Е^2.
Ax=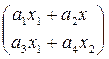 ; (Ax,x)=
; (Ax,x)= 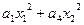 +
+ ;
;
(b,x)= 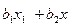
Пример:
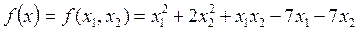
f(x) – квадратичная функция в E^2. Поэтому x* должна быть найдена после 2-х итераций метода сопряжённых градиентов.
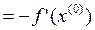 .
.
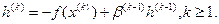
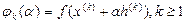 .
.
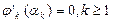 .
.
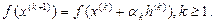
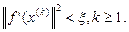
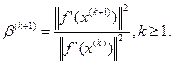
Пусть начальное приближение 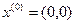 .
.
1-ая итерация: k=0
1. 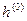
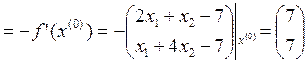
2. 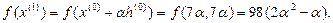
Решаем задачу минимизации 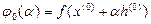 по α. Из условия минимума
по α. Из условия минимума 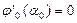 получим
получим 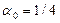 . Отсюда находим
. Отсюда находим
3. 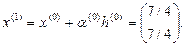
4. 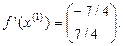
5. 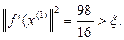
Условие остановки не выполнено.
2-ая итерация: k=1
6. 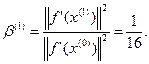
7. 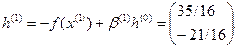
8. 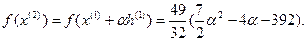
Решаем задачу минимизации 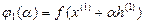 по α. Из условия минимума
по α. Из условия минимума 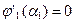 получим
получим 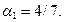
9. 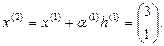
10. 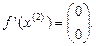
11. 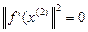 , тогда x*=
, тогда x*=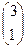 – решение задачи.
– решение задачи.
4. Минимизация функции F(x) методом барьерных функций:
Пример:
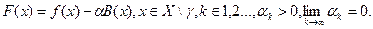
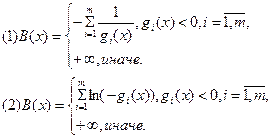
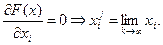
Пример:
1. 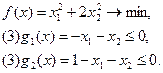
По (1):
Последовательность задач безусловной минимизации принимает вид:
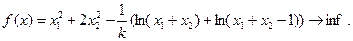
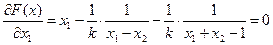
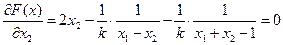
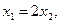
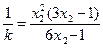
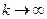
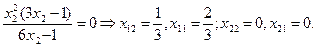
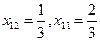 принадлежит заданной области (3),а
принадлежит заданной области (3),а 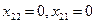 не принадлежит, тогда x*=(1/3,2/3) - решение.
не принадлежит, тогда x*=(1/3,2/3) - решение.
– Конец работы –
Используемые теги: Лабораторная, работа, Элементарная, Теория, погрешностей0.072
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Лабораторная работа №1 «Элементарная теория погрешностей»
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов