рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ.
Реферат Курсовая Конспект
СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ.
СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ. - раздел Математика, МАТРИЦЫ И ИХ ВИДЫ Пусть Даны Три Вектора ...
Пусть даны три вектора 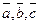 . Так как для векторов введены два вида произведений – скалярное и векторное, то для трех векторов относительно операции умножения существуют следующие виды произведений:
. Так как для векторов введены два вида произведений – скалярное и векторное, то для трех векторов относительно операции умножения существуют следующие виды произведений:
1) двойное векторное произведение, т.е. произведение, в котором вначале находится векторное произведение двух из заданных векторов, затем векторное произведение полученного вектора на третий из данных векторов.
Например, вначале находится векторное произведение 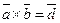 , затем – векторное произведение
, затем – векторное произведение  ;
;
2) смешанное произведение, т.е. произведение, в котором вначале находится векторное произведение двух из заданных векторов, затем скалярное произведение полученного вектора на третий из данных векторов.
Например, вначале находится векторное произведение 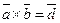 , затем – скалярное произведение
, затем – скалярное произведение  .
.
Двойное векторное произведение обозначается в форме  или в форме
или в форме  .
.
Ясно, что результатом двойного векторного произведения является вектор.
Смешанное или иначе векторно-скалярное произведение обозначается символом 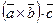 или символом
или символом 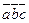 . Результатом смешанного произведения является число.
. Результатом смешанного произведения является число.
Пусть требуется определить смешанное произведение векторов, если известны координаты этих векторов
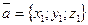 ,
, 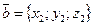 ,
, 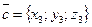 .
.
Вычислим предварительно 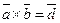 . Имеем
. Имеем
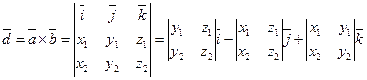 .
.
Воспользовавшись формулой (57), найдем
 .
.
Полученное равенство, согласно теореме о разложении определителя по элементам строки, можно переписать в форме
 . (62)
. (62)
Формула (62) дает возможность для смешанного произведения в координатной форме. Заметим, что в этой формуле координаты векторов 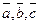 записаны соответственно в первой, второй и третьей строках определителя.
записаны соответственно в первой, второй и третьей строках определителя.
Покажем, что для смешанного произведения векторов справедливы равенства
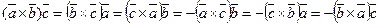 . (63)
. (63)
Проверим, например, справедливость равенства 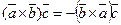 . Согласно формуле (62) имеем
. Согласно формуле (62) имеем
 .
.
Как известно, при перестановке двух строк определителя знак определителя меняется на противоположный. Тогда, умножая обе части предыдущего равенства на (-1), получим
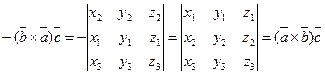 .
.
Итак, 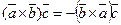 .
.
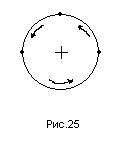 Формулы (63) проще всего запомнить с помощью правила круговой перестановки векторов, сущность которого пояснена на рис.25 и 26.
Формулы (63) проще всего запомнить с помощью правила круговой перестановки векторов, сущность которого пояснена на рис.25 и 26.
|
|

|
|
|
|
|
 . Отложим векторы
. Отложим векторы 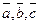 от общего
от общего
 | ||||
| ||||
| ||||
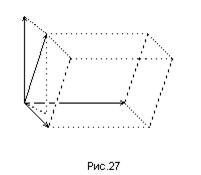
начала и построим на этих векторах, как на ребрах, параллелепипед (рис.27). Пусть 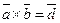 . Тогда, согласно определению векторного произведения векторов, модуль вектора
. Тогда, согласно определению векторного произведения векторов, модуль вектора  равен площади
равен площади 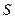 gараллелограмма, построенного на векторах
gараллелограмма, построенного на векторах  , как на сторонах. Следовательно,
, как на сторонах. Следовательно,
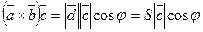 ,
,
где 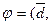 ^
^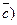 и
и  .
.
Обозначим через  высоту параллелепипеда, опущенную из конца вектора
высоту параллелепипеда, опущенную из конца вектора 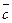 на рассматриваемый параллелограмм, и выясним смысл произведения
на рассматриваемый параллелограмм, и выясним смысл произведения 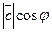 . Вектор
. Вектор  перпендикулярен плоскости параллелограмма, тогда
перпендикулярен плоскости параллелограмма, тогда
 , если
, если  и
и
 , если
, если  .
.
Следовательно, если  есть объем параллелепипеда, то
есть объем параллелепипеда, то
 , если
, если  и
и
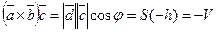 , если
, если  .
.
Итак,  или
или 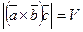 . (64)
. (64)
Равенство (64) означает, что модуль смешанного произведения трех векторов равен объему параллелепипеда, построенного на этих векторах, как на ребрах.
Следствие (условие компланарности трех векторов). Для того, чтобы три вектора 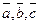 были компланарны, необходимы и достаточно, чтобы их смешанное произведение равнялось нулю, т.е.
были компланарны, необходимы и достаточно, чтобы их смешанное произведение равнялось нулю, т.е.  или в координатной форме
или в координатной форме
 . (65)
. (65)
Необходимость. Пусть векторы 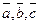 компланарны. Тогда вектор
компланарны. Тогда вектор  перпендикулярен плоскости, в которой расположены данные векторы, следовательно, перпендикулярен вектору
перпендикулярен плоскости, в которой расположены данные векторы, следовательно, перпендикулярен вектору 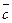 . Поэтому
. Поэтому
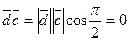 . Следовательно,
. Следовательно,  .
.
Достаточность. Пусть 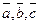 таковы, что
таковы, что  .
.
Если предположить, что векторы не компланарны, то на них можно построить параллелепипед с объемом 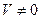 . Но, согласно формуле (64),
. Но, согласно формуле (64),  . Следовательно,
. Следовательно,  или
или  , что противоречит исходному утверждению.
, что противоречит исходному утверждению.
ПРИМЕР 20.1. Вычислить объем треугольной пирамиды с вершинами в точках 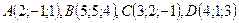 .
.
Решение. Построим три вектора
 с общим началом точкой
с общим началом точкой 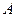 . На этих векторах, как на ребрах, построим параллелепипед. Его объем равен
. На этих векторах, как на ребрах, построим параллелепипед. Его объем равен  . Объем пирамиды
. Объем пирамиды  составляет шестую долю объема параллелепипеда. Следовательно,
составляет шестую долю объема параллелепипеда. Следовательно,
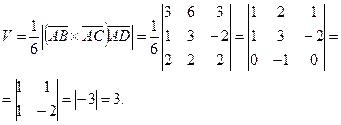
Ответ: 3.
Из геометрического смысла смешанного произведения векторов и рассмотренного примера следует, что оно широко используется при вычислении объемов любых многогранников.
– Конец работы –
Эта тема принадлежит разделу:
МАТРИЦЫ И ИХ ВИДЫ
ОПЕРАЦИИ НАД МАТРИЦАМИ... Равенство матриц... Две матрицы А и В называются равными А В если они имеют одинаковые размеры и их соответствующие элементы равны...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ.
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?


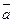
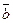






Новости и инфо для студентов