рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Философия
- /
- ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
Реферат Курсовая Конспект
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА - раздел Философия, Федеральное Агентство По Образованию ...
Федеральное агентство по образованию
Сибирская государственная автомобильно-дорожная академия
(СибАДИ)
А. М. Лукин, Д. А. Лукин, В.В. Квалдыков
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
(разделы «Статика», «Кинематика»)
Учебно-методическое пособие для студентов
заочной и дистанционной форм обучения при подготовке
дипломированного специалиста по направлению
«СТРОИТЕЛЬСТВО»
Омск
Издательство СибАДИ
| |
ББК 22.21
УДК 531.8
Л 84
Рецензенты:
д-р техн. наук, проф. В. В. Сыркин (СибАДИ);
канд. техн. наук В. Я. Слободин (СибАДИ)
Рекомендовано к изданию редакционно-издательским советом
академии в качестве учебно-методического пособия
А. М. Лукин, Д. А. Лукин, В. В. Квалдыков
ISBN 978–5–93204–318–9ВВЕДЕНИЕ
Развитие современной техники ставят перед её разработчиками разнообразные задачи, связанные с проектированием технических объектов: строительных конструкций и сооружений, машин различного функционального назначения и т. д. Несмотря на разнообразие этих объектов, решения поставленных задач основываются на принципах, которые имеют общую научную базу. Объясняется это тем, что в большинстве задач значительное место занимают вопросы, требующие изучения законов равновесия или движения механических систем.
Теоретическая механика представляет собой одну из научных основ современных технических дисциплин, таких как теория механизмов и машин, сопротивление материалов, детали машин и т. д. Теоретическая механика является одним из разделов механики.
Механика – наука о механическом движении и механическом взаимодействии материальных тел.
Теоретическая механика – раздел механики, в котором изучают законы движения механических систем и общие свойства этих движений.
Курс теоретической механики состоит из трёх разделов: статика, кинематика, динамика. Как правило, изучение теоретической механики начинают с первого раздела – статики.
Настоящее учебно-методическое пособие по разделам «Статика», «Кинематика» теоретической механики предназначено для студентов заочной и дистанционной форм обучения. Такое содержание данного пособия обусловлено тем, что эти разделы теоретической механики студенты изучают в одном семестре.
Необходимость создания учебно-методического пособия вызвана тем, что студенты дистанционной и заочной форм обучения не всегда имеют свободный доступ к учебной литературе и консультациям преподавателя. Эта проблема особенно актуальна для студентов, проживающих в глубинных сельских районах и на Крайнем Севере.
Следует также отметить, что опубликованные ранее вузовские учебники по теоретической механике очень объёмны. Как правило, в рабочих программах этой дисциплины при подготовке дипломированного специалиста по направлению «СТРОИТЕЛЬСТВО» в настоящее время используется не более 50 % информации, приведённой в рекомендуемой для высшего профессионального образования учебной литературе. Студентам дистанционной и заочной форм обучения, самостоятельно изучающим учебный материал, достаточно сложно ориентироваться в обширном списке рекомендуемой литературы при поиске теоретических положений, необходимых для выполнения контрольных работ.
Кроме этого, имеется ещё один существенный недостаток известных учебных пособий, заключающийся в следующем. Для одних и тех же специальностей дневной и заочной форм обучения применяются различные задания. Парадокс в том, что для студентов заочной формы обучения эти задания гораздо труднее, чем для студентов дневной формы обучения.
Содержание данного учебно-методического пособия соответствует программе и требованиям государственного образовательного стандарта ГОС ВПО РФ по дисциплине «Теоретическая механика» (разделы «Статика», «Кинематика») при подготовке дипломированного специалиста по направлению «СТРОИТЕЛЬСТВО».
Отличительными особенностями данного учебно-методического пособия от многих известных учебников по теоретической механике являются следующие особенности:
1. Краткость изложения теоретического материала. Громоздкие выводы и доказательства в нём не приведены, но вместе с тем уделено большое внимание чёткости формулировок определений основных понятий, теорем и принципов. Это позволяет глубже уяснить физический смысл формул и математических выражений, описывающих изучаемые механические процессы. В книге приведено достаточное количество рисунков, наглядно иллюстрирующих теоретический материал.
2. Сформирован подробный словарь терминов и определений, используемых в изучаемых разделах теоретической механики. Это позволяет студенту выработать чёткие навыки владения грамотной инженерно-технической лексикой.
3. Теория, примеры решения задач, варианты курсовых заданий, алгоритмы решения и примеры их выполнения сведены в одну книгу. Это существенно повышает удобства при изучении теоретического курса.
4. К каждой изучаемой теме занятий приведены вопросы для самоконтроля. Такие же вопросы сформулированы и для изучаемого в соответствующем семестре учебного материала. По этим вопросам студент имеет возможность самостоятельно проверить качество усвоения теоретического материала по всему комплексу вопросов, изучаемых в теоретической механике. По результатам самостоятельно проведённой проверки студент выявляет те вопросы, которые изучены недостаточно хорошо, и принимает решение о целесообразности коррекции своих знаний по изучаемому предмету.
5. В качестве контрольных работ использованы задания, аналогичные заданиям, приведенным в «Сборнике заданий для курсовых работ по теоретической механике»: Учеб. пособие для техн. вузов/ А. А. Яблонский, С. С. Норейко, С. А. Вольфсон и др.; Под ред. А. А. Яблонского. – 4-е изд., перераб. и доп. – М.: Высш. шк., 1985. – 367 с., ил. Это учебное пособие применяется практически во всех высших учебных заведениях Российской Федерации.
6. Рассмотрены приёмы решения типовых задач, которые используются при сдаче интернет-экзамена.
Такой подход к выбору вариантов заданий позволяет обеспечить единство требований государственных образовательных стандартов РФ к качеству высшего образования и поднять качество дистанционного и заочного образования до уровня очного образования.
Перечисленные особенности делают данный курс легко доступным для хорошего понимания и усвоения студентами изучаемого материала, позволяют в короткие сроки подготовиться к экзаменам и зачётам.
Настоящее учебно-методическое пособие является вторым изданием, переработанным и дополненным. Идя навстречу многочисленным пожеланиям студентов, использующим эту книгу в качестве учебно-методического пособия, авторы внесли дополнительные разделы курса теоретической механики.
Хочется надеяться, что и впредь читатели будут помогать совершенствованию книги своими предложениями, которые будут с благодарностью рассмотрены.
Авторы выражают глубокую благодарность рецензентам и редактору за внимательное прочтение рукописи и замечания, которые позволили в значительной мере улучшить содержание книги.
ПРОГРАММА ДИСЦИПЛИНЫ
«ТЕОРЕТИЧЕСКАЯ МЕХАНИКА»
(разделы «Статика», «Кинематика»)
Программа дисциплины «Теоретическая механика» (разделы «Статика», «Кинематика») составлена согласно требованиям государственного образовательного стандарта ГОС ВПО РФ по дисциплине «Теоретическая механика» при подготовке дипломированных специалистов по направлению «СТРОИТЕЛЬСТВО».
Выдержка из ГОС ВПО РФ по дисциплине
«Теоретическая механика»
Требования
Индекс Наименование дисциплин и их основные разделы Всего часов ЕН.Ф.06 …Цели и задачи дисциплины
Задачей изучения дисциплины является получение студентами практических навыков в области теоретической механики, приобретение ими умения… Изучение студентами теоретической механики основывается на предварительной… Знания, полученные студентами при изучении теоретической механики и последующих общетехнических дисциплин, применяются…Требования к уровню освоения содержания дисциплины
Студент должен знать:
– понятийный аппарат теоретической механики;
– навыки составления математических моделей практических задач, в которых приходится иметь дело с равновесием или движением твёрдых тел;
– технику составления уравнений равновесия или движения различных механических систем;
– основные приёмы аналитического и численного исследований уравнений равновесия и движения.
Студент должен знать и уметь использовать:
– основные законы механики и важнейшие следствия из них;
– основные модели механики (модель материальной точки, системы материальных точек, абсолютно твёрдого тела, системы взаимосвязанных твёрдых тел);
– основные аналитические и численные методы исследования механических систем.
Студент должен иметь опыт решения типовых задач по статике и кинематике механических систем.
ОБЩИЕ ПОЛОЖЕНИЯ
В полном курсе теоретической механики студенты изучают три её раздела:… Назначение изучаемого предмета – дать будущим специалистам основные сведения о законах равновесия и движения…Рекомендуется следующий порядок решения
Контрольных работ
2. Задания решают в общем виде (в буквенных обозначениях), а затем, подставляя численные значения, вычисляют результат с точностью до трёх значащих… 3. Перед тем как оформить решённое задание, следует тщательно проверить все… 4. Если возможно, следует проверить правильность ответа, решив задание вторично каким-либо иным путем.Основные понятия статики
В основу каждого раздела механики положен ряд понятий и определений, принята система аксиом, т. е. важнейших положений, многократно подтверждённых практикой. Приступая к изучению статики, следует определить основные понятия, встречающиеся в этом разделе механики.
Статика – раздел механики, в котором изучают условия равновесия механических систем под действием сил.
Масса – одна из основных характеристик любого материального объекта, определяющая его инертные и гравитационные свойства.
Масса является мерой инертности точки и мерой инертности тела при его поступательном движении. Масса измеряется в кг.
Инертность – свойство материального тела, проявляющееся в сохранении движения, совершаемого им при отсутствии действующих сил, и в постепенном изменении этого движения с течением времени, когда на тело начинают действовать силы.
Материальная точка – точка, имеющая массу.
Материальная точка не имеет размеров и обладает способностью взаимодействовать с другими материальными точками.
Абсолютно твёрдое тело – материальное тело, в котором расстояние между двумя любыми точками остается неизменным (рис. 1.1).
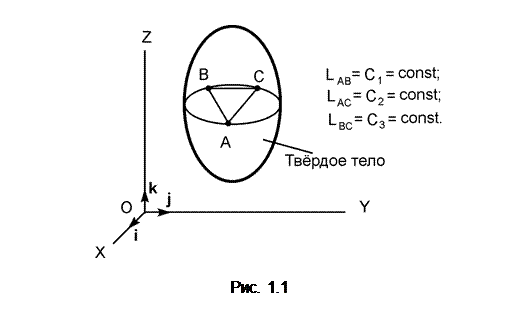 |
В природе такие тела отсутствуют, так как каждое тело деформируется в результате приложенных воздействий. Однако принятое допущение (абсолютно твёрдое тело) значительно упрощает изучение действия сил на тело и условий, при которых эти силы уравновешиваются. В дальнейшем абсолютно твёрдые тела условлено называть телами.
Механическая система – любая совокупность материальных точек.
Движения материальных точек в механической системе взаимозависимы. В механике тело рассматривают как механическую систему, образованную непрерывной совокупностью материальных точек. Тела могут взаимодействовать друг с другом.
Механическое действие – действие на данное тело со стороны других тел, которое приводит к изменению скоростей точек этого тела или следствием которого является изменение взаимного положения точек данного тела.
Другими словами, при механическом действии тело приобретает механическое движение.
Механическое движение – изменение с течением времени взаимного положения тел в пространстве или взаимного положения частей данного тела.
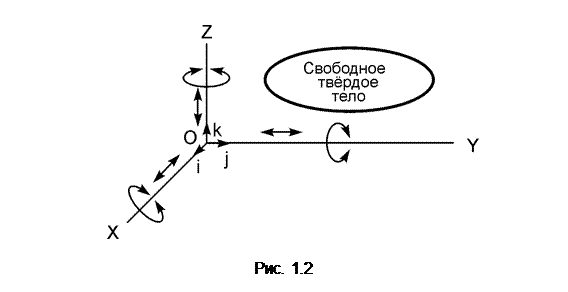 |
Таким образом, тело либо деформируется, либо перемещается в пространстве. Деформацию тел изучает наука – сопротивление материалов. Так как в теоретической механике имеют дело с абсолютно твёрдыми телами, то при механическом действии тела изменяют свое положение в пространстве относительно друг друга. В общем случае тело может поступательно перемещаться в пространстве по трём направлениям (параллельно координатным осям OX, OY, OZ) и вращаться относительно этих осей (рис. 1.2).
Свободное тело – тело, на перемещения которого в пространстве не наложено никаких ограничений.
Следовательно, свободное тело может осуществлять в системе отсчёта OXYZ шесть движений. Другими словами, тело имеет шесть степеней свободы.
Тело может находиться в состоянии покоя, которое является частным случаем механического движения, когда скорости точек рассматриваемого тела равны нулю. Если тело покоится, то говорят, что оно находится в состоянии равновесия.
Равновесие механической системы – состояние механической системы, при котором её точки под действием приложенных сил остаются в покое по отношению к рассматриваемой системе отсчёта.
Система отсчёта – система координат, связанная с телом, по отношению к которому определяется положение других тел (механических систем) в разные моменты времени.
Важнейшим понятием в теоретической механике является понятие силы.
Сила – векторная величина, являющаяся мерой механического действия одного тела на другое.
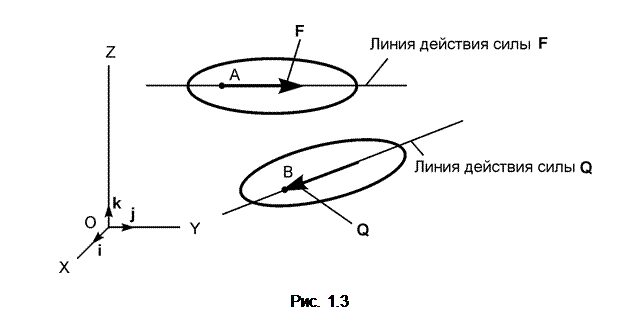
Сила как вектор определяется тремя элементами: числовым значением (модулем), направлением и точкой приложения. Графически силу изображают направленным прямолинейным отрезком (вектором), совпадающим по направлению с направлением силы (рис. 1.3).
|
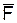 ,
, 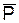 ,
,  .
.
Линия действия силы – прямая линия, вдоль которой направлен вектор, изображающий силу.
Простейшим примером силы является сила тяжести, с которой тело притягивается к Земле.
Сила тяжести – сила, действующая на материальную точку вблизи земной поверхности, равная произведению массы m этой точки на ускорение gсвободного падения в вакууме.
G= m·g.
Сила тяжести G прикладывается в центре С тяжести тела и направлена к центру Земли (по вертикали). В неподвижной (НСО) относительно Земли системе отсчёта OXYZ сила тяжести тела изображается так, как это показано на рис. 1.4.
Если речь идет о величине (модуле) силы тяжести тела, то употребляют термин «вес тела».
Вес тела – сумма модулей сил тяжести, действующих на частицы этого тела.
Вес G тела находят по формуле
G = m·g.
Силы имеют различную физическую природу, например, сила давления пара, сила притяжения наэлектризованных тел и т. д. В теоретической механике не рассматривают физическую природу сил, здесь важны только величина, направление и точка приложения силы. Модуль силы измеряют в ньютонах [H].
Силы, действующие на механическую систему, делят на две группы: внешние и внутренние.
Внешняя сила – сила, действующая на какую-либо точку механической системы со стороны тел, не принадлежащих рассматриваемой механической системе.
Внешние силы принято обозначать символами: FiE, RiE.
Внутренние силы – силы, действующие на какие-либо точки механической системы со стороны других точек, принадлежащих рассматриваемой механической системе.
Внутренние силы принято обозначать символом RiJ.
Система сил – любая совокупность сил, действующих на механическую систему.
Систему сил принято обозначать (F1,…,Fn).
Уравновешенная система сил – система сил, которая будучи приложена к свободному телу, находящемуся в равновесии, не выводит его из этого кинематического состояния.
Уравновешивающая система сил – система сил, которая вместе с заданной другой системой сил составляет уравновешенную систему сил.
Эквивалентные системы сил – две или несколько систем сил, имеющих одну и ту же уравновешивающую систему сил.
Эквивалентные системы сил приводят свободное тело в одно и то же кинематическое состояние. Для обозначения эквивалентности систем сил используют знак «~».
Равнодействующая системы сил – сила, эквивалентная данной системе сил.
Плоская система сил – система сил, линии действия которых расположены в одной плоскости.
Сходящаяся система сил – система сил, линии действия которых пересекаются в одной точке.
Из курса физики известно, что равнодействующая сходящейся системы сил графически определяется по правилу силового многоугольника (рис. 1.5).
При построении силового многоугольника равнодействующая R соединяет начало первого вектора с концом последнего. Силовой многоугольник не замкнут.
Таким образом, сходящаяся система сил имеет равнодействующую R, определяемую векторным равенством:
R =F1 +…+ F4.
В общем случае для системы сходящихся сил (F1,…,Fn) используют векторное равенство R = Σ Fi.

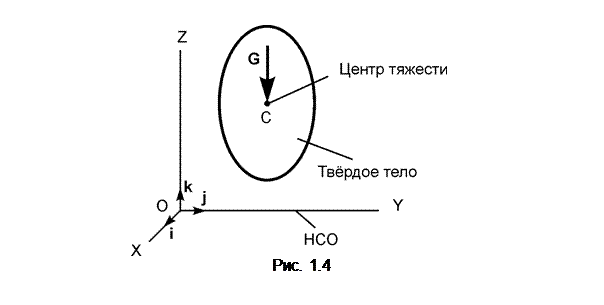
Уравновешенную систему сил графически изображают замкнутым силовым многоугольником, в котором конец последнего вектора приходит в начало первого вектора (рис. 1.6).
Такую систему сил описывают равенством R = F1 +…+ F4 = 0. В общем случае для уравновешенной системы сил (F1,…,Fn) справедливо равенство R = Σ Fi = 0.
Силы делят на сосредоточенные и распределённые.
Сосредоточенная сила – сила, приложенная к телу в какой-либо одной его точке.
Распределённые силы – силы, действующие на все точки некоторой части линии, поверхности или объёма.
Понятие о сосредоточенной силе является условным, так как практически приложить силу в точке нельзя. Силу, которую в механике рассматривают как сосредоточенную, представляет собой равнодействующую некоторой системы распределённых сил.
Распределённые силы характеризуются величиной q интенсивности распределения силы, т. е. величиной силы на единицу объёма, поверхности или длины линии. Интенсивность распределения силы может иметь следующие размерности: Н/м3; Н/м2; Н/м. На тела в основном действуют параллельные и сходящиеся распределённые силы. К параллельным силам, распределённым по объёму, относятся силы тяжести частиц тела.
Поскольку все аксиомы и теоремы статики формулируются для сосредоточенных сил, необходимо рассмотреть способы перехода от распределённых сил к сосредоточенным силам.
Рассмотрим замену линейно распределённых сил сосредоточенной силой.

Равнодействующую распределённых на линии параллельных сил постоянной интенсивности q определяют по формуле Q = q×L, где L – длина балки (рис. 1.7).
Равнодействующая распределённых сил (сосредоточенная сила) прикладывается к балке под центром тяжести площади прямоугольника.
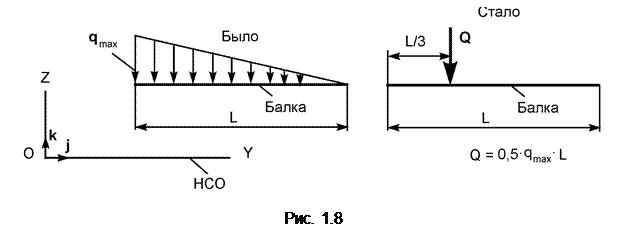
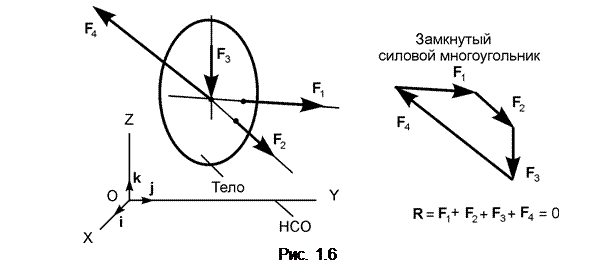
В инженерной практике часто применяют нагрузку, интенсивность которой изменяется по закону треугольника (рис. 1.8).
Равнодействующую параллельных распределённых сил на линии с интенсивностью, изменяющейся по закону треугольника, определяют по формуле Q = 0,5qmax×L, где qmax – наибольшая интенсивность. Линия действия сосредоточенной силы Q смещена в сторону наибольшей интенсивности и проходит через центр тяжести площади треугольника.
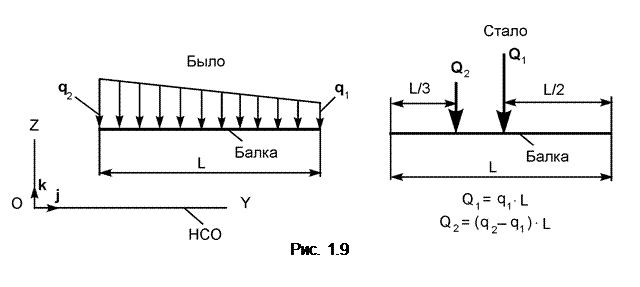
В более сложных случаях распределённые нагрузки заменяют несколькими сосредоточенными силами. Пример такой замены приведен на рис. 1.9.
Модули Q1, Q2 сил Q1, Q2 определяют по формулам:
Q1 = q1·L; Q2 = 0,5·(q2 – q1)·L.
Аксиомы статики
1. Аксиома инерции. Под действием уравновешенной системы сил (ΣFi = 0 или (F1,…, Fn) ~ 0) свободное тело находится в состоянии покоя или равномерного прямолинейного движения.
2. 
Аксиома равновесия двух сил. Две силы, приложенные к телу, уравновешиваются только в том случае, если их модули равны и они направлены по одной прямой в противоположные стороны (рис. 1.10).
3. Аксиома присоединения и исключения уравновешенной системы сил. Действие системы сил на тело не изменится, если к ней присоединить или из неё исключить уравновешенную систему сил.
Следствие 1
Не изменяя кинематического состояния тела, силу можно переносить по линии действия, сохраняя неизменными её модуль и направление (рис. 1.11). Так как силу можно переносить в любую точку её линии действия, то силу…Вопросы и задания для самоконтроля
1. Сформулировать определение термина «механика».
2. Сформулировать определение термина «теоретическая механика».
3. Сформулировать определение термина «статика».
4. Сформулировать определение термина «масса».
5. Сформулировать определение термина «инертность».
6. Сформулировать определение термина «материальная точка».
7. Сформулировать определение термина «абсолютно твёрдое тело».
8. Сформулировать определение термина «механическая система».
9. Сформулировать определение термина «механическое действие».
10. Сформулировать определение термина «механическое движение».
11. Сформулировать определение термина «свободное тело».
12. Сформулировать определение термина «равновесие механической системы».
13. Сформулировать определение термина «система отсчёта».
14. Сформулировать определение термина «сила».
15. Сформулировать определение термина «линия действия силы».
16. Сформулировать определение термина «сила тяжести».
17. Сформулировать определение термина «вес тела».
18. Сформулировать определение термина «внешняя сила».
19. Сформулировать определение термина «внутренние силы».
20. Сформулировать определение термина «система сил».
21. Сформулировать определение термина «уравновешенная система сил».
22. Сформулировать определение термина «уравновешивающая система сил».
23. Сформулировать определение термина «эквивалентные системы сил».
24. Сформулировать определение термина «равнодействующая системы сил».
25. Сформулировать определение термина «плоская система сил».
26. Сформулировать определение термина «сходящаяся система сил».
27. Сформулировать определение термина «сосредоточенная сила».
28. Сформулировать определение термина «распределённые силы».
29. Сформулировать аксиому инерции.
30. Сформулировать аксиому равновесия двух сил.
31. Сформулировать аксиому присоединения и исключения уравновешенной системы сил.
32. Сформулировать первое следствие из аксиомы присоединения и исключения уравновешенной системы сил.
33. Сформулировать второе следствие из аксиомы присоединения и исключения уравновешенной системы сил.
34. Сформулировать аксиому параллелограмма сил.
35. Сформулировать аксиому равенства действия и противодействия.
36. Сформулировать аксиому равновесия сил, приложенных к деформирующемуся телу при его затвердевании.
37. Записать формулу для определения равнодействующей системы сходящихся сил.
38. Записать формулу для определения модуля сосредоточенной силы при действии на балку распределённой нагрузки с интенсивностью q, изменяющейся по закону прямоугольника.
39. Записать формулу для определения модуля сосредоточенной силы при действии на балку распределённой нагрузки с интенсивностью q, изменяющейся по закону треугольника.
40. Используя аксиому параллелограмма сил, записать формулу для определения модуля равнодействующей двух сходящихся сил.
41. Используя правило треугольника, записать формулу, связывающую модули двух сходящихся сил и их равнодействующую.
42. Записать формулу, выражающую аксиому равновесия двух сил.
Связи и реакции связей
Несвободное тело – тело, на перемещения которого в пространстве наложены…Шарнирно-подвижная и неподвижная опоры
Реакция RA шарнирно-подвижной опоры направлена по нормали к опорной поверхности в сторону балки. Шарнирно-подвижная опора поставлена на катки,… Шарнирно-неподвижная опора препятствует поступательным перемещениям балки… На рис. 1.22 изображена балка АВ. По аксиоме параллелограмма сил, которая допускает обратное толкование, реакцию RВ…Необходимо еще раз подчеркнуть, что разложение силы на составляющие силы производится только в точке приложения силы.
Вопросы и задания для самоконтроля
1. Сформулировать определение термина «несвободное тело».
2. Сформулировать определение термина «связи».
3. Сформулировать определение термина «реакции связей».
4. Сформулировать определение термина «гладкая связь».
5. Сформулировать определение термина «гибкая связь».
6. Сформулировать определение термина «невесомый стержень».
7. Сформулировать определение термина «свободное тело».
8. Сформулировать аксиому связей.
Проекции силы на ось и плоскость
Пусть линия действия силы F лежит в плоскости…Аналитический способ сложения сил
Проекция равнодействующей сходящейся системы сил на какую-либо ось равна…Аналитические условия равновесия
Системы сходящихся сил
В случае если силы взаимно уравновешиваются, их равнодействующая равна нулю. Аналитически это выражается соответствующими уравнениями равновесия.
Для пространственной системысходящихся сил уравнения равновесия имеют вид:
Σ FiOX = 0; Σ FiOY = 0; Σ FiOZ = 0.
Для плоской сходящейся системы сил уравнения равновесия приводятся к виду:
Σ FiOX = 0; Σ FiOY = 0.
Для равновесия системы сходящихся сил необходимо и достаточно, чтобы суммы проекций этих сил на каждую из координатных осей системы отсчёта равнялись нулю.
При помощи этих уравнений можно решить задачи на равновесие сходящейся системы сил на плоскости и в пространстве.
Алгоритм решения задач статики
Как правило, в задачах статики по известным активным силам FiE требуется… Σ FiE + Σ RiE = 0.Алгоритм решения задач статики
1. Выбирают систему отсчёта.
2. Выбирают тело, к которому приложена система уравновешивающихся сил.
3. Показывают все действующие на тело активные нагрузки.
4. Согласно аксиоме связей действие связей на тело заменяют соответствующими реакциями связей.
5. К полученной системе сил применяют уравнения равновесия, соответствующие этой системе сил.
6. Из уравнений равновесия определяют неизвестные величины.
Пример решения задачи
На плоскую сходящуюся систему сил
Определить реакции стержней АС, ВС, если угол a = 60о.Вопросы и задания для самоконтроля
1. Сформулировать определение термина «проекция силы на ось».
2. Записать формулы для определения проекций силы F на координатные оси декартовой системы отсчёта OXYZ.
3. Записать формулу для определения силы F через компоненты этой силы в декартовой системе отсчёта OXYZ.
4. Записать формулы для определения направляющих косинусов силы в декартовой системе отсчёта OXYZ.
5. Записать формулы для определения проекций равнодействующей системы сходящихся сил в декартовой системе отсчёта OXYZ.
6. Записать формулу, выражающую геометрическое условие равновесия сходящейся системы сил.
7. Записать уравнения равновесия для пространственной системы сходящихся сил в декартовой системе отсчёта OXYZ.
8. Записать уравнения равновесия для плоской системы сходящихся сил в декартовой системе отсчёта OXYZ.
Пара сил
Пару сил в механике рассматривают как одно из основных понятий, наряду с… Пара сил – система двух параллельных, противоположно направленных и равных по модулю сил, не лежащих на одной…Сложение пар сил

Пусть заданы три пары сил, плоскостями действия которых являются плоскости OXY, OXZ, OYZ (рис. 1. 37).
Векторные моменты этих пар сил обозначим М1, М2, М3. Так как эти векторы свободные, то переместив их в начало системы отсчёта OXYZ, получим систему векторов, приложенных в одной точке. Сложив графически эти векторы, получим один вектор М= М1 + М2 + М3.
Если таких векторов много, то в общем случае имеем M = Σ Mi (см. рис. 1.37).
Векторный момент пары сил, эквивалентный данной системе пар сил в пространстве, равен сумме векторных моментов заданных пар сил.
Условия равновесия пар сил
Теорема. Для равновесия пар сил, действующих на тело, необходимо и достаточно, чтобы величина векторного момента эквивалентной пары сил равнялась… M = Σ Mi = 0.Вектор момента силы относительно точки
Момент силы F относительно точки О изображается вектором MО(F), приложенным в… Модуль MО(F) этого вектора (MО(F)) равен произведению модуля F силы F на её плечо h…Алгебраический момент силы
Относительно точки
На рис. 1.39 изображены сила F и точки А и В, расположенные в плоскости OYZ. …Вопросы и задания для самоконтроля
1. Сформулировать определение термина «пара сил».
2. Сформулировать определение термина «плоскость действия пары сил».
3. Сформулировать определение термина «плечо пары сил».
4. Сформулировать определение термина «алгебраический момент пары сил».
5. Сформулировать определение термина «момент пары сил».
6. Сформулировать теорему об эквивалентности пар сил, лежащих в одной плоскости.
7. Сформулировать первое следствие из теоремы об эквивалентности пар сил, лежащих в одной плоскости.
8. Сформулировать второе следствие из теоремы об эквивалентности пар сил, лежащих в одной плоскости.
9. Сформулировать теорему о равновесии пар сил, приложенных к телу.
10. Сформулировать определение термина «плечо силы относительно точки».
11. Записать формулу для определения алгебраического момента силы F относительно точки А.
Приведение силы к заданному центру
Теорема. Силу F, не изменяя её действие на тело, можно перенести из точки её приложения А в любой центр приведения О,…Приведение произвольной системы сил
К заданному центру
Теорема. Любую произвольную систему сил, действующую на тело, можно привести в…Аналитические условия равновесия
Плоской произвольной системы сил
Плоская произвольная система сил – система сил, линии действия которых…Другие типы связей на плоскости
На рис. 1.45 изображена жёсткая заделка… Таким образом, реакция жёсткой заделки состоит из двух сил XA, YA, расположенных параллельно координатным осям, и…Варианты курсового задания С 1
«Определение реакций опор твёрдого тела»
Для закрепления теоретического материала необходимо выполнить курсовое задание С 1.
В курсовом задании (см. табл. 1.1) приведены варианты плоских балок, загруженных активными нагрузками Р, М, q, где Р – сосредоточенная сила; М – алгебраический момент пары сил; q – интенсивность распределённой нагрузки.
Используя основную форму уравнений равновесия для плоской произвольной системы сил, определить реакции внешних связей, наложенных на балку. Применяя другую форму уравнений равновесия, проверить правильность расчётов.
Таблица 1.1
| Номер варианта | Расчётная схема | Исходные данные | Определяемые величины |

| Р1 = 10 кН; Р2 = 20 кН; М = 6 кН·м; q = 2 кН/м | ZA = ? YA = ? RB = ? | |
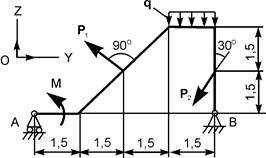
| Р1 = 20 кН; Р2 = 20 кН; М = 5 кН·м; q = 4 кН/м | ZB = ? YB = ? RA = ? | |

| Р1 = 10 кН; Р2 = 20 кН; М = 4 кН·м; q = 1 кН/м | ZA = ? YA = ? RB = ? | |
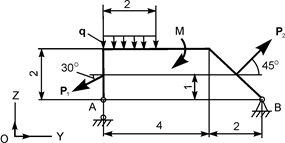
| Р = 10 кН; М = 6 кН·м; q = 2 кН/м | ZB = ? YB = ? RA = ? |
Продолжение табл. 1.1
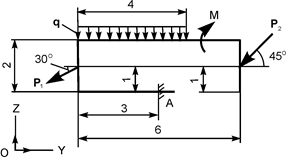
| Р1 = 20 кН; Р2 = 20 кН; М = 5 кН·м; q = 4 кН/м | ZA = ? YA = ? MA = ? | |

| Р1 = 2 кН; Р2 = 20 кН; М = 4 кН·м; q = 2 кН/м | ZА = ? YА = ? MA = ? | |
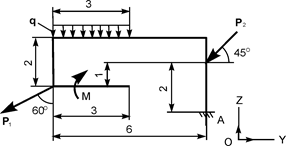
| Р1 = 10 кН; Р2 = 20 кН; М = 6 кН·м; q = 2 кН/м | ZA = ? YA = ? МА = ? | |
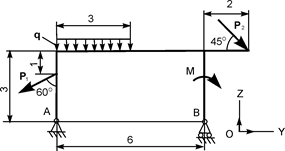
| Р1 = 4 кН; Р2 = 20 кН; М = 10 кН·м; q = 3 кН/м | ZA = ? YA = ? RB = ? |
Продолжение табл. 1.1

| Р1 = 10 кН; Р2 = 20 кН; М = 5 кН·м; q = 2 кН/м | ZA = ? YA = ? RB = ? | |
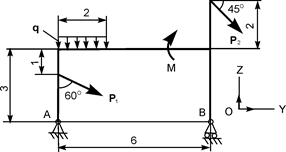
| Р1 = 15 кН; Р2 = 20 кН; М = 4 кН·м; q = 3 кН/м | ZA = ? YA = ? RB = ? | |

| Р1 = 10 кН; Р2 = 20 кН; М = 5 кН·м; q = 2 кН/м | ZA = ? YA = ? МА = ? | |
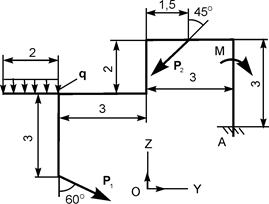
| Р1 = 12 кН; Р2 = 20 кН; М = 6 кН·м; q = 2 кН/м | ZA = ? YA = ? МА = ? |
Продолжение табл. 1.1

| Р1 = 10 кН; Р2 = 20 кН; М = 6 кН·м; q = 2 кН/м | ZA = ? YA = ? RB = ? | |
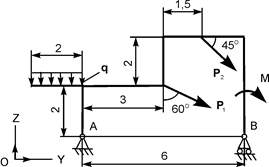
| Р1 = 20 кН; Р2 = 20 кН; М = 12 кН·м; q = 2 кН/м | ZA = ? YA = ? RB = ? | |
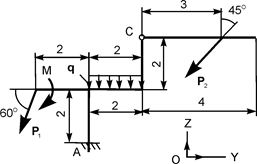
| Р1 = 20 кН; Р2 = 20 кН; М = 4 кН·м; q = 3 кН/м | ZA = ? YA = ? МА = ? | |
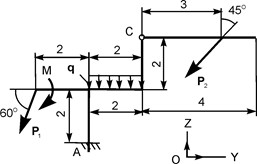
| Р1 = 14кН; Р2 = 20 кН; М = 4 кН·м; q = 3 кН/м | ZA = ? YA = ? МА = ? |
Продолжение табл. 1.1

| Р1 = 10 кН; Р2 = 20 кН; М = 6 кН·м; q = 4 кН/м | ZA = ? YA = ? RB = ? | |
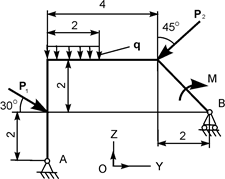
| Р1 = 20 кН; Р2 = 20 кН; М = 10 кН·м; q = 2 кН/м | ZA = ? YA = ? RB = ? | |

| Р1 = 10 кН; Р2 = 20 кН; М = 4 кН·м; q = 2 кН/м | ZВ = ? YВ = ? RА = ? | |
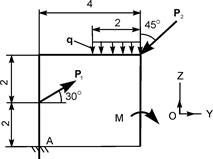
| Р1 = 6 кН; Р2 = 20 кН; М = 6 кН·м; q = 1 кН/м | ZA = ? YA = ? MA = ? |
Продолжение табл. 1.1
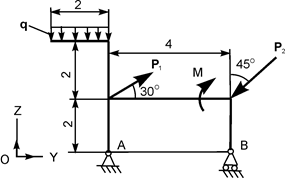
| Р1 = 4 кН; Р2 = 20 кН; М = 2 кН·м; q = 1 кН/м | ZA = ? YA = ? RB = ? | |

| Р1 = 20 кН; Р2 = 20 кН; М = 5 кН·м; q = 2 кН/м | ZA = ? YA = ? МА = ? | |
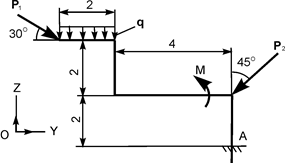
| Р1 = 5 кН; Р2 = 10 кН; М = 2 кН·м; q = 3 кН/м | ZA = ? YA = ? МА = ? | |

| Р1 = 10 кН; Р2 = 20 кН; М = 6 кН·м; q = 1 кН/м | ZA = ? YA = ? MA = ? |
Продолжение табл. 1.1

| Р1 = 6 кН; Р2 = 20 кН; М = 8 кН·м; q = 2 кН/м | ZA = ? YA = ? MA = ? | |
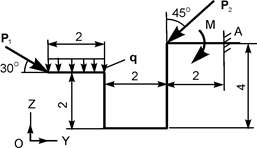
| Р1 = 20 кН; Р2 = 20 кН; М = 10 кН·м; q = 2 кН/м | ZA = ? YA = ? MA = ? | |
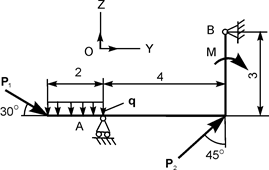
| Р1 = 10 кН; Р2 = 20 кН; М = 10 кН·м; q = 3 кН/м | ZB = ? YB = ? RA = ? | |

| Р1 = 15 кН; Р2 = 20 кН; М = 8 кН·м; q = 1 кН/м | ZA = ? YA = ? МА = ? |
Окончание табл. 1.1

| Р = 5 кН; Р2 = 20 кН; М = 2 кН·м; q = 1 кН/м | ZA = ? YA = ? MА = ? | |

| Р = 10 кН; Р2 = 20 кН; М = 6 кН·м; q = 2 кН/м | ZA= ? YA = ? MА = ? |
Следует ещё раз отметить, что номер варианта задания в контрольной работе студент выбирает самостоятельно, используя методику, приведённую в общих положениях данного пособия.
Цели контрольной работы С 1:
1. Научить студента составлять и решать уравнения равновесия для плоской произвольной системы сил, приложенных к одному телу.
2. Научить студента проводить проверку правильности проведённых результатов расчётов.
Пример выполнения курсового задания С 1
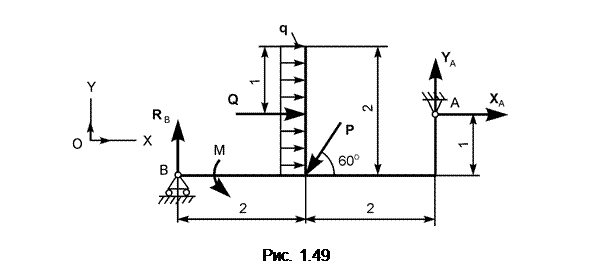 |
На рис. 1.49 изображена расчётная схема балки.
Дано: P = 20 кН; M = 10 кН·м; q = 2 кНм. Определить реакции внешних связей в точках А и В.
Решение.
Определение реакций внешних связей для рассматриваемой балки проводится согласно алгоритму решения задач статики, приведённому в подразделе 1.7.
1. Выбирается система отсчёта. Так как балка плоская, то выбирается система отсчёта OXY.
2. Выделяется тело, равновесие которого рассматривается. В нашем случае таким телом является балка, изображённая на рис. 1.49.
3. К балке прикладываются активные нагрузки. По условию задачи активные нагрузки известны. Так как задана распределённая нагрузка с интенсивностью q, то её приводят к сосредоточенной силе Q, модуль которой определяют по формуле Q = q×L = 2×2 = 4 кН. Эту сосредоточенную силу прикладывают к телу и показывают размер, на котором она приложена. Таким образом, на балку действуют следующие активные нагрузки: P, Q – активные силы; активная пара сил с алгебраическим моментом М.
4. Согласно аксиоме связей внешние связи, наложенные на механическую систему в точках А и В, отбрасывают и показывают реакции внешних связей XA, YA, RB. Таким образом, на балку действуют внешние нагрузки, состоящие из активных нагрузок: P, Q, M и реакций внешних связей: XA, YA, RB.
5. Так как система внешних сил, действующих на тело, является плоской и произвольной, то записывают три уравнения равновесия:
Σ + Σ
+ Σ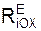 = 0 = Q – P·cos(60о) + XA = 0; (1)
= 0 = Q – P·cos(60о) + XA = 0; (1)
Σ + Σ
+ Σ = 0 = – P·sin(60о) + RB + YA = 0; (2)
= 0 = – P·sin(60о) + RB + YA = 0; (2)
Σ MA(FiE) + Σ MA(RiE) = 0 =
= M + P·sin(600)×2 – P·cos(60о)·1 – RB×4 = 0. (3)
При составлении выражений (1), (2), (3) использована первая форма уравнений равновесия. Эти уравнения решают в наиболее удобной последовательности и находят проекции неизвестных реакций на координатные оси системы отсчёта OXY или модули этих реакций.
Из уравнения (1) XA= – Q + P·cos(60о) = – 4 + 20×0,5 = 6,000 кН.
Из уравнения (3) RB = (M + P·sin(60о)×2 – P·cos(60о)×1)4 =
= (10 + 20×0,866×2 – 20×0,5×1)4 = 8,660 кН.
Из уравнения (2)
YA= – RB + P·sin(60о) = – 8,66 +20×0,866 = 8,660 кН.
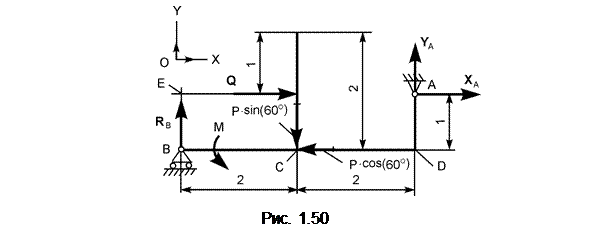 |
Согласно условию задания необходимо произвести проверку правильности проведённых расчётов. С целью такой проверки изобразим рассматриваемую балку в упрощённом варианте (рис. 1.50).
Сила Р разложена на составляющие силы по координатным осям. Это упрощает проецирование силы Р на координатные оси системы отсчёта OXY. Необходимо отметить, что силы раскладываются на составляющие по координатным осям системы отсчёта только в точке их приложения. Порядок решения задачи остается прежним, только использована третья форма уравнений равновесия.
Σ MС(FiE) + Σ MС(RiE) = 0 =
= M – Q·1 – RB·2 + YA·2 – XA·1 = 0; (4)
Σ MD(FiE) + Σ MD(RiE) = 0 =
= M – Q·1 + P·sin(60о)·2 – RB·4 – XA·1 = 0; (5)
Σ MЕ(FiE) + Σ MЕ(RiE) = 0 =
= M – P·sin(600)·2 – P·cos(60о)·1 + YA·4 = 0. (6)
Подставляя найденные значения реакций XA, YA, RB в выражения (4), (5), (6) и вычислив, получим:
Σ MС(FiE) + Σ MС(RiE) = 0 =
= 10 – 4·1 – 8,660·2 + 8,660·2 – 6·1 = 0; (4I)
Σ MD(FiE) + Σ MD(RiE) = 0 =
= 10 – 4·1 + 20·0,866·2 – 8,660·4 – 6·1 = 0; (5I)
Σ MЕ(FiE) + Σ MЕ(RiE) = 0 =
= 10 – 20·0,866·2 – 20·0,5·1 + 8,660·4 = 0. (6I)
Проведённая проверка подтвердила правильность результатов расчётов. Результаты вычислений помещают в таблицу.
Таблица
| Реакции и их размерность | XA ,кН | YA ,кН | RB ,кН |
| Численные значения реакций | 6,000 | 8,660 | 8,660 |
Общие рекомендации по выполнению курсового задания
1.На каждом чертеже должны быть размеры. Чертежи выполняются в масштабе.
2.Силы следует раскладывать в точках их приложения на составляющие по координатным осям системы отсчёта.
3.Выбирается та форма уравнений равновесия, которая обеспечивает минимум вычислительных работ. В уравнении моментов рекомендуется находить точки, где пересекается наибольшее число линий действия сил.
4.Производится проверка правильности результатов расчётов.
Вопросы и задания для самоконтроля
1. Сформулировать определение понятия «плоская произвольная система сил».
2. Сформулировать теорему, выражающую метод Пуансо для произвольной системы сил.
3. Записать геометрическое условие равновесия произвольной системы сил.
4. Записать первую форму уравнений равновесия плоской произвольной системы сил.
5. Записать вторую форму уравнений равновесия плоской произвольной системы сил.
6. Записать третью форму уравнений равновесия плоской произвольной системы сил.
7. Записать векторную формулу для определения главного вектора сил.
8. Записать формулу для определения модуля главного вектора сил в декартовой системе отсчёта.
9. Записать векторную формулу для определения главного момента системы сил относительно центра приведения.
1.20. Расчёт фермы
Фермой называется геометрически неизменяемая шарнирно-стержневая конструкция. При этом все стержни фермы прямолинейные. Если оси всех стержней фермы лежат в одной плоскости, то её называют плоской фермой. Точки, в которых сходятся оси стержней, называют узлами фермы, а те узлы, которыми ферма опирается на основания, называют опорными узлами. Стержни плоской фермы, расположенные по верхнему контуру, образуют верхний пояс, а расположенные по нижнему контуру – нижний пояс фермы. Вертикальные стержни называют стойками, а наклонные раскосами.
На рис. 1.51 изображена плоская ферма, состоящая из 17 стержней.
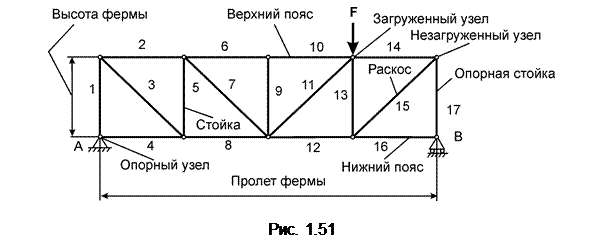 |
Совокупность стержней 2, 6, 10, 14 образует верхний пояс фермы, а совокупность стержней 4, 8, 12, 16 образует нижний пояс фермы.
В теоретической механике рассматривают идеализированные фермы, при расчёте которых приняты следующие допущения:
1. Все внешние нагрузки к ферме прикладываются только в узлах.
2. Все шарниры считаются идеальными, т. е. трение в узлах фермы не учитывается.
3. Все стержни невесомые, т. е. они загружены только по концам.
4. Все силы, действующие на ферму, лежат в одной плоскости.
На каждый из стержней фермы действуют две силы, приложенные к его концам, которые при равновесии могут быть направлены только вдоль стержня. Следовательно, можно считать, что стержни фермы работают только на растяжение или сжатие.
В реальных фермах может и не быть шарниров, а при жёстком соединении сваркой или заклёпками стержни могут воспринимать и другие виды нагрузок (изгиб, кручение и т. д.). Однако результаты вычислений при принятых допущениях вполне пригодны для практики, причем расчёт усилий в стержнях существенно облегчается.
1.21. Методология расчёта усилий
В стержнях плоской фермы
1.21.1. Варианты курсового задания С 2Аналитический и графический способы
Вырезания узлов
При использовании способа вырезания узлов вырезают узел фермы и прикладывают к… Рассмотрим изображённую на рис. 1.52 плоскую ферму, загруженную сосредоточенными силами F1, F2, F3.Решение.
Порядок решения задач статики приведён в подразделе 1.7 данного пособия. Рассматривается равновесие всей фермы как абсолютно твёрдого тела. Как… Система внешних сил (F1, F2, F3, RA, XB, YB), действующих на ферму, плоская… Σ+ Σ= 0 = – F1 – RA + XB = 0; (1)Б. Определение усилий в стержнях способом
Вырезания узлов
Система сил (F3, S11, S12), действующая на узел, плоская сходящаяся. Аналитические условия равновесия такой системы сил выражаются системой… Σ+ Σ= 0 = – S12 – S11·cos(α) = 0; (1) Σ+ Σ= 0 = – F3 + S11·sin(α) = 0. (2)Решение.
S7 = = = 5,000 кН. Σ M(II)(FiE) + Σ M(II)(RiE) = 0 = = F2·b + F3·b·tg(α) + S5·b·tg(α) = 0; (2)Вопросы и задания для самоконтроля
1. Сформулировать определение термина «ферма».
2. Сформулировать определение термина «плоская ферма».
3. Сформулировать определение термина «узел фермы».
4. Сформулировать определение термина «опорный узел фермы».
5. Сформулировать определение термина «загруженный узел фермы».
6. Сформулировать определение термина «стойка».
7. Сформулировать определение термина «раскос».
8. Сформулировать определение термина «верхний пояс фермы».
9. Сформулировать определение термина «нижний пояс фермы».
10. Сформулировать определение термина «нулевой стержень».
11. Сформулировать первую лемму для определения нулевых стержней.
12. Сформулировать вторую лемму для определения нулевых стержней.
13. Сформулировать третью лемму для определения нулевых стержней.
14. Сформулировать определение термина «точка Риттера».
Определение реакций опор составных
Конструкций
Статически определимые задачи – задачи, в которых реакции внешних связей…Алгоритм решения задач
На определение реакций внешних связей
Для составных конструкций
Существует целый класс задач на равновесие составной конструкции, которые… 1. Выбирается система отсчёта.Варианты курсового задания С 3
«Определение реакций опор составной конструкции
(система двух тел)»
Методологию расчёта реакций внешних связей, наложенных на составную конструкцию, рассмотрим на примере выполнения курсового задания С 3, которое входит в контрольную работу обучающегося.
Конструкция состоит из двух тел. Определить реакции внешних связей, наложенных на составную конструкцию. Варианты расчётных схем конструкций и приложенные к ним нагрузки приведены в табл. 1.3.
Таблица 1.3
| Номер варианта | Расчётная схема | Исходные данные | Определяемые величины |
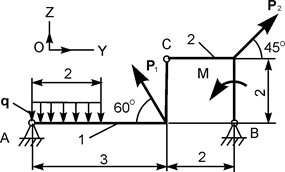
| Р1 = 10 кН; Р2 = 10 кН; М = 6 кН·м; q = 2 кН/м | ZA = ? YA = ? ZВ = ? YВ = ? | |
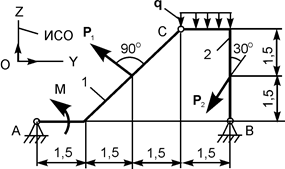
| Р1 = 6 кН; Р2 = 10 кН; М = 12 кН·м; q = 1 кН/м | ZA = ? YA = ? ZВ = ? YВ = ? |
Продолжение табл. 1.3

| Р1 = 8 кН; Р2 = 10 кН; М = 3 кН·м; q = 2 кН/м | ZA = ? YA = ? ZВ = ? YВ = ? | |
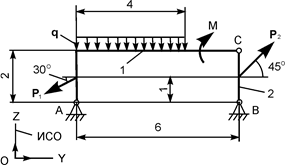
| Р1 = 5 кН; Р2 = 12 кН; М = 4 кН·м; q = 2 кН/м | ZA = ? YA = ? ZВ = ? YВ = ? | |
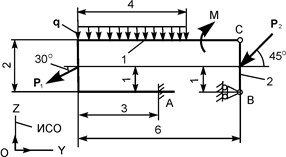
| Р1 = 6 кН; Р2 = 8 кН; М = 3 кН·м; q = 2 кН/м | ZA = ? YA = ? MA = ? RВ = ? | |
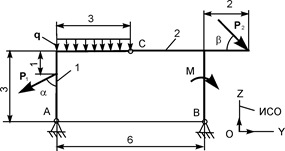
| Р1 = 4 кН; Р2 = 6 кН; М = 10 кН·м; q = 2 кН/м | ZA = ? YA = ? ZB = ? YВ = ? |
Продолжение табл. 1.3

| Р1 = 7 кН; Р2 = 8 кН; М = 15 кН·м; q = 2 кН/м | RA = ? ZB = ? YВ = ? MВ = ? | |

| Р1 = 8 кН; Р2 = 8 кН; М = 16 кН·м; q = 2 кН/м | ZA = ? YA = ? ZВ = ? YВ = ? | |
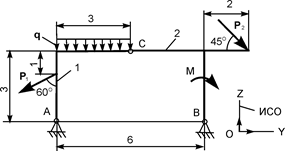
| Р1 = 10 кН; Р2 = 10 кН; М = 6 кН·м; q = 2 кН/м | ZA = ? YA = ? ZВ = ? YВ = ? | |
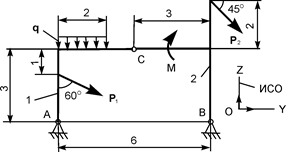
| Р1 = 10 кН; Р2 = 3 кН; М = 9 кН·м; q = 2 кН/м | ZA = ? YA = ? ZВ = ? YВ = ? |
Продолжение табл. 1.3
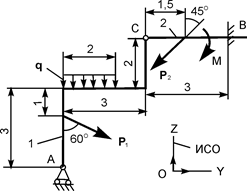
| Р1 = 12 кН; Р2 = 5 кН; М = 6 кН·м; q = 1 кН/м | RA = ? ZB = ? YВ = ? MВ = ? | |
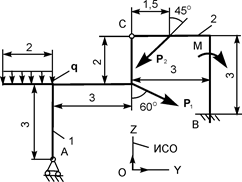
| Р1 = 11 кН; Р2 = 3 кН; М = 8 кН·м; q = 4 кН/м | RA = ? ZB = ? YВ = ? MВ = ? | |
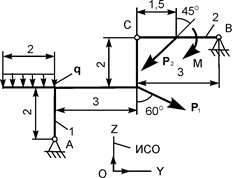
| Р1 = 10 кН; Р2 = 12 кН; М = 8 кН·м; q = 2 кН/м | ZA = ? YA = ? ZВ = ? YВ = ? | |
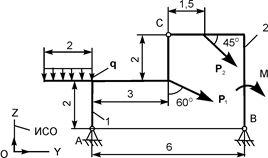
| Р1 = 10 кН; Р2 = 2 кН; М = 12 кН·м; q = 2 кН/м | ZA = ? YA = ? ZВ = ? YВ = ? |
Продолжение табл. 1.3
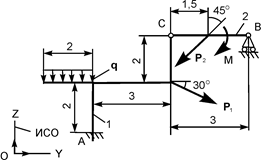
| Р1 = 15 кН; Р2 = 10 кН; М = 5 кН·м; q = 2 кН/м | ZA = ? YA = ? MA = ? RВ = ? | |
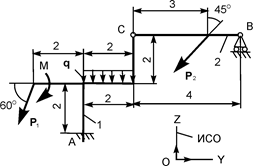
| Р1 = 16 кН; Р2 = 10 кН; М = 4 кН·м; q = 1 кН/м | ZA = ? YA = ? MA = ? RВ = ? | |
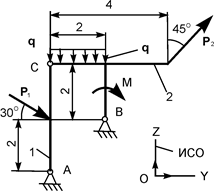
| Р1 = 17 кН; Р2 = 3 кН; М = 6 кН·м; q = 6 кН/м | ZA = ? YA = ? ZВ = ? YВ = ? | |
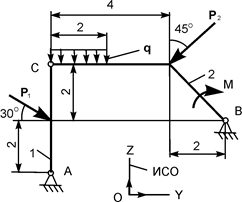
| Р1 = 18 кН; Р2 = 9 кН; М = 4 кН·м; q = 8 кН/м | XA = ? YA = ? XВ = ? YВ = ? |
Продолжение табл. 1.3
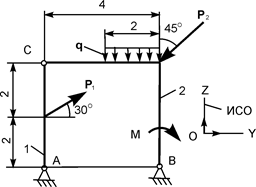
| Р1 = 19 кН; Р2 = 7 кН; М = 12 кН·м; q = 2 кН/м | ZA = ? YA = ? ZВ = ? YВ = ? | |

| Р1 = 20 кН; Р2 = 12 кН; М = 8 кН·м; q = 4 кН/м | ZA = ? YA = ? MA = ? RВ = ? | |
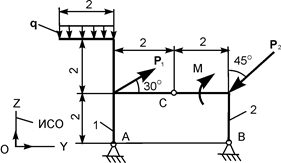
| Р1 = 21 кН; Р2 = 10 кН; М = 12 кН·м; q = 6 кН/м | ZA = ? YA = ? ZВ = ? YВ = ? | |

| Р1 = 22 кН; Р2 = 12 кН; М = 10 кН·м; q = 5 кН/м | XA = ? YA = ? MA = ? RВ = ? |
Продолжение табл. 1.3
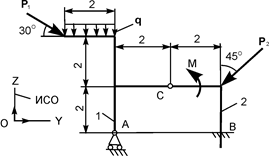
| Р1 = 23 кН; Р2 = 9 кН; М = 5 кН·м; q = 8 кН/м | RA = ? ZB = ? YВ = ? MВ = ? | |
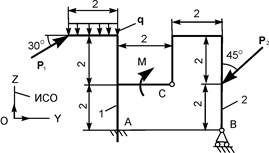
| Р1 = 24 кН; Р2 = 10 кН; М = 12 кН·м; q = 2 кН/м | ZA = ? YA = ? MA = ? RВ = ? | |
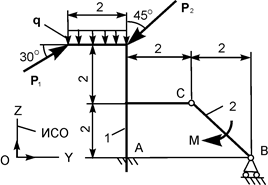
| Р1 = 25 кН; Р2 = 10 кН; М = 8 кН·м; q = 2 кН/м | ZA = ? YA = ? MA = ? RВ = ? | |
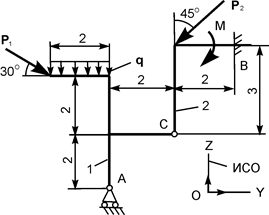
| Р1 = 26 кН; Р2 = 16 кН; М = 6 кН·м; q = 6 кН/м | RA = ? ZB = ? YВ = ? MВ = ? |
Окончание табл. 1.3
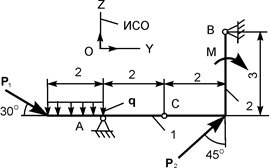
| Р1 = 27 кН; Р2 = 10 кН; М = 4 кН·м; q = 3 кН/м | ZA = ? YA = ? ZВ = ? YВ = ? | |
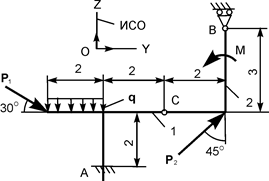
| Р1 = 28 кН; Р2 = 18 кН; М = 8 кН·м; q = 2 кН/м | ZA = ? YA = ? MA = ? RВ = ? | |
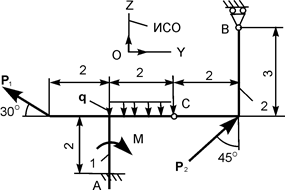
| Р1 = 28 кН; Р2 = 20 кН; М = 6 кН·м; q = 2 кН/м | ZA = ? YA = ? MA = ? RВ = ? | |

| Р1 = 30 кН; Р2 = 20 кН; М = 6 кН·м; q = 1 кН/м | RA = ? ZB = ? YВ = ? MВ = ? |
Пример выполнения курсового задания С 3

В качестве примера, иллюстрирующего порядок расчёта составной конструкции, рассматривается равновесие механической системы, состоящей из двух тел, соединенных между собой внутренним шарниром в точке D (рис. 1.62).
Дано: Р1 = 2 кН; Р2 = 4 кН; М = 6 кН·м; q = 2 кН/м.
Определить реакции внешних связей в точках А, В, С.
Решение.
Распределённая нагрузка интенсивностью q заменяется сосредоточенной силой Q, модуль которой равен:
Q = q·L = 2·4 = 8 кН.
К механической системе, состоящей из тел 1 и 2, приложены активные силы P1, P2, Q и активная пара сил с алгебраическим моментом М, а также реакции XA, YA, RB, Rc внешних связей. Так как система сил, действующих на совокупность тел 1 и 2 плоская произвольная, то составляются три уравнения равновесия.
Σ + Σ
+ Σ = 0 =
= 0 =
= P1·cos(60о) + P2·sin(45о) + XA – RB·sin(45о) – Rc·sin(45о) = 0; (1)
Σ + Σ
+ Σ = 0 =
= 0 =
= – Q – P1·sin(60о) – P2·cos(45о) + YA +
+ RB·cos(45о) + Rc·cos(45о) = 0; (2)
Σ MD(FiE) + Σ MD(RiE) = 0 =
= Q·6 + P1·sin(60о)·2 + P2·3 – М – YA·8 – RB·6 + RC·6 = 0. (3)
Так как имеются три уравнения равновесия, в которые входят четыре неизвестные реакции XA, YA, RB, RC, то такая система уравнений не решается. Поэтому конструкцию расчленяют по внутренней связи в точке D и рассматривают равновесие каждого тела в отдельности.

На рис. 1.63 изображено тело 1, которое находится в покое под действием активных сил Q, P1, реакций внешних связей XA, YA и реакций внутренних связей XD, YD.
Следует отметить, что для тела 1 силы Q, P1, XA, YA, XD, YD являются внешними силами.
Система сил, действующая на тело 1, плоская произвольная, поэтому для неё составляется три уравнения равновесия.
Σ + Σ
+ Σ = 0 =
= 0 =
= 0 = P1·cos(60о) + XA + XD = 0; (4)
Σ + Σ
+ Σ = 0 =
= 0 =
= – Q – P1·sin(60о) + YA + YD = 0; (5)
Σ MD(FiE) + Σ MD(RiE) = 0 =
= Q·6 + P1·sin(60о)·2 – YA·8 = 0. (6)
На рис. 1.63 реакции XD, YD внутренней связи показывают, как тело 2 действует на тело 1 в точке D.
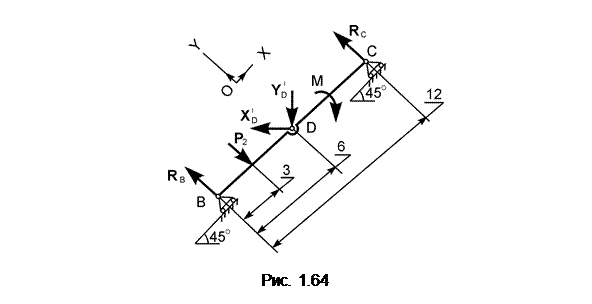
Рассматривается равновесие тела 2, на которое действуют активная сила Р2, активная пара сил с алгебраическим моментом М, реакции RB, RC внешних связей в точках В и С и реакции XDI, YDI внутренней связи в точке D (рис. 1.64).
Реакции XDI, YDI показывают, как тело 1 действует на тело 2 в точке D. По аксиоме равенства действия и противодействия эти реакции направлены противоположно одноименным реакциям, показанным на рис. 1.63.
 |
XD = – XDI; YD = – YDI; XD = XDI; YD = YDI.
По отношению к телу 2 активные нагрузки Р, М и реакции RB, RC, XDI, YDI являются внешними нагрузками.
Таким образом, на тело 2 действует плоская произвольная система сил, поэтому составляют три уравнения равновесия. С целью сокращения формы записи уравнений равновесия использована система отсчёта OXY, одна из осей которой направлена вдоль стержня ВС.
Σ + Σ
+ Σ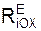 = 0 =
= 0 =
= – XDI·cos(45о) – YDI·cos(45о) = 0; (7)
Σ + Σ
+ Σ = 0 =
= 0 =
= – P2 + RB + XDI·sin(45о) – YDI·sin(45о) + Rc = 0; (8)
Σ MD(FiE) + Σ MD(RiE) = 0 =
= P2·3 – M – RB·6 + RC·6 = 0. (9)
Таким образом, по рис. 1.62, 1.63, 1.64 составлено девять уравнений равновесия, в которые вошли шесть неизвестных реакций. С целью сокращения времени расчёта целесообразно использовать уравнения равновесия, составленные для тел 1 и 2 механической системы.
Из уравнения (6) определяется проекция реакции YA на координатную ось OY:
YA = (Q·6 + P1·sin(60о)·2)/8 = (8·6 + 2·0,866·2)/8 = 6,433 кН.
Из уравнения (5) имеем
YD = – YA + Q + P1·sin(60о) = – 6,433 + 8 + 2·0,866 = 3,299 кН.
Из уравнения (7) определяется проекция реакции XD внутренней связи в точке D на координатную ось ОХ:
XD = XDI = – YD = – 3,299 кН.
Из уравнения (4) определяется проекция реакции XA на ось ОХ:
XA = – P1·cos(60о) – XD = – 2·0,5 – (–3,299) = 2,299 кН.
С учётом выражения (7) уравнения (8) и (9) несложно преобразовать в систему уравнений (8I), (9I):
RB – P2 + 2·XD·cos(45о) + RC = 0; (8I)
– RB + P2·(3/6) – (M/6) + RC = 0. (9I)
Складывая левые и правые части этих уравнений, получим уравнение
– 0,5·P2 – (M/6) + 2·XD·cos(45о) + 2·RC = 0. (10)
Из уравнения (10) находим модуль реакции RC:
RC = (0,5·P2 + (M/6) – 2·XD·cos(45о))/2 =
= (0,5·4 + (6/6) – 2·(– 2,299)·0,707)/2 = 3,832 кН.
Возвращаясь к уравнению (9I), находим модуль реакции RB:
RB = P2·(3/6) – (M/6) + RC = 4·(3/6) – (6/6) + 3,832 = 4, 832 кН.
Таким образом, при совместном решении уравнений (4) – (9) определяются реакции XA, YA, RB, RC внешних связей в точках А, В, С и реакции XD, YD, XDI, YDI внутренней связи механической системы в точке D.
Для проверки полученных результатов расчётов используются уравнения (1), (2), (3):
Σ + Σ
+ Σ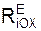 = 0 =
= 0 =
= P1·cos(60о) + P2·sin(45о) + XA – RB·sin(45о) – Rc·sin(45о) = 0 =
= 2·0,5 + 4·0,707 + 2,299 – 4,832·0,707 – 3,832·0,707 = 0; (1)
Σ + Σ
+ Σ = 0 =
= 0 =
= – Q – P1·sin(60о) – P2·cos(45о) + YA +
+ RB·cos(45о) + Rc·cos(45о) = 0 =
= – 8 – 2·0,866 – 4·0,707 + 6,433 +
+ 4,832·0,707 + 3,832·0,707 = 0; (2)
Σ MD(FiE) + Σ MD(RiE) = 0 =
= Q·6 + P1·sin(60о)·2 + P2·3 – М – YA·8 – RB·6 + RC·6 = 0 =
= 8·6 + 2·0,866·2 + 4·3 – 6 – 6,433·8 – 4,832·6 + 3,832·6 = 0. (3)
Проверка показала, что расчёты проведены правильно.
Результаты проведенных расчётов помещают в таблицу.
Таблица
| Проекции реакций внешних связей на координатные оси | Проекции реакции внутренней связи на координатные оси | ||||
| XA, кН | YA, кН | RB, кН | RC, кН | XD, кН | YD, кН |
| 2,299 | 6,433 | 4,832 | 3,832 | –3,299 | 3,299 |
Таким образом, если необходимо определить реакции внешних связей для составной конструкции, то следует расчленить конструкцию по внутренней связи и рассмотреть равновесие каждого тела.
Для решения некоторых задач на составную конструкцию может быть использована теорема о равновесии трёх непараллельных сил.
Теорема. Линии действия трёх непараллельных взаимно уравновешивающихся сил, лежащих в одной плоскости, пересекаются в одной точке.
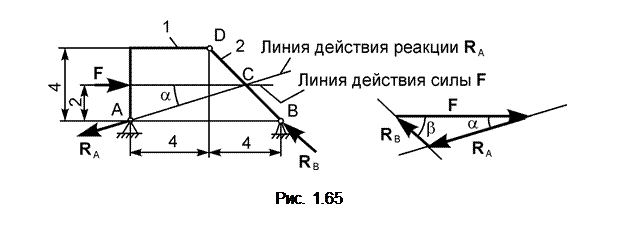 |
На рис. 1.65 изображена составная конструкция из двух тел, соединённых между собой внутренним шарниром в точке D.
Дано. На тело 1 действует активная сила F. Тело 2 загружено только по его концам В и D. Исходя из этого, тело 2 можно считать невесомым стержнем.
Определить реакции внешних связей.
Решение. На механическую систему, состоящую из двух тел, действуют три взаимно уравновешивающиеся внешние силы: активная сила F и реакции RA, RB в шарнирно-неподвижных опорах А и В. Так как тело 2 является невесомым стержнем, то линия действия реакции RB проходит по стержню 2. Линии действия силы F и реакции RB пересекаются в точке C. Так как три силы F, RA и RB не параллельны и лежат в одной плоскости, то линия действия реакции RA тоже должна проходить через точку C.
Система сил (F, RA, RB) уравновешенная, поэтому силовой треугольник, построенный на этих силах, должен быть замкнут (см. рис. 1.65). Для определения величин реакций используется теорема синусов:
F/sin(α+β) = RB/sin(α) = RA/sin(β).
Величина угла α находится из рис. 1.65 по формулам:
tg(α)= 2/6 = 0,333; α = arctg(0,333) = 18,434o.
Величина угла β = 45o. Это так же видно из рис. 1.65. Окончательно находим:
RA =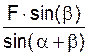 =
= 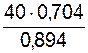 = 31,633 кН;
= 31,633 кН;
RВ =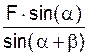 =
= 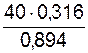 = 14,138 кН.
= 14,138 кН.
Действительное направление реакций RA и RB показано на силовом треугольнике.
Эту задачу можно решить и по изложенному ранее алгоритму. Однако такое решение требует больших расчётных работ.
Вопросы и задания для самоконтроля
1. Сформулировать определение понятия «статически определимые задачи».
2. Сформулировать определение понятия«статически неопределимые задачи».
3. Записать алгоритм решения задач статики для составных конструкций.
4. Сформулировать теорему о трёх непараллельных взаимно уравновешивающихся сил.
Пространственная произвольная
Система сил
1.26.1. Момент силы относительно осиВарианты курсового задания С 4
«Определение реакций опор твёрдого тела»
Для закрепления изложенного теоретического материала необходимо выполнить курсовое задание С 4.
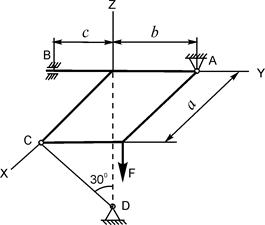
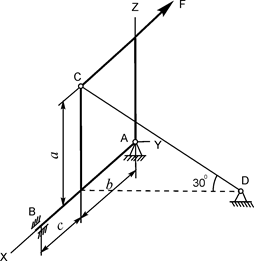
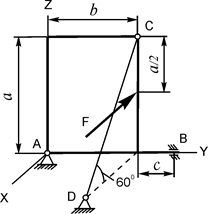
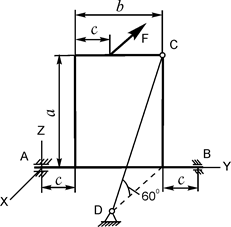
В вариантах 1 - 15 этого курсового задания (табл. 1.4) рассматривается равновесие однородной прямоугольной плиты с размерами a и b и весом G. На плиту действует активная сила F, которая параллельна соответствующей координатной оси системы отсчёта OXYZ. Требуется определить реакции внешних связей, наложенных на плиту. По условию задания CD – невесомый стержень.
В вариантах 16 – 30 рассматривается равновесие вала, на котором установлены два круглых колеса с радиусами R1, R2. Эти колёса загружены активными силами F1 – F5. По условию задания активные силы параллельны соответствующим координатным осям системы отсчёта OXYZ. Требуется определить реакции внешних связей, наложенных на конструкцию, и величину силы F4.
Исходные данные для расчёта и определяемые величины приведены в табл. 1.4.
Таблица 1.4
| Номер варианта | Расчётная схема | Исходные данные | Определяемые величины |
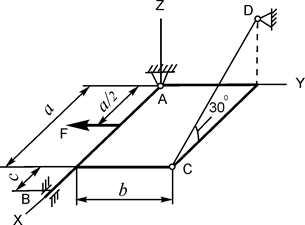
| G = 8 кН; F = 5 кН; a = 3 м; b = 2 м; c = 0,2 м | XA = ? YA = ? ZA = ? YB = ? ZB = ? RC = ? | |
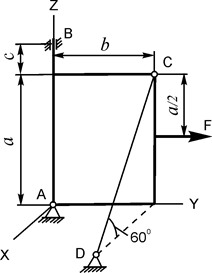
| G = 8 кН; F = 6 кН; a = 3 м; b = 2 м; c = 0,2 м | XA = ? YA = ? ZA = ? YB = ? XB = ? RC = ? |
Продолжение табл. 1.4

| G = 8 кН; F = 7 кН; a = 3 м; b = 2 м; c = 0,2 м | XA = ? YA = ? ZA = ? YB = ? ZB = ? RC = ? | |
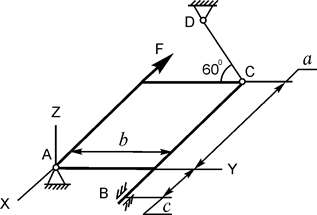
| G = 8 кН; F = 8 кН; a = 3 м; b = 2 м; c = 0,2 м | XA = ? YA = ? ZA = ? YB = ? ZB = ? RC = ? | |
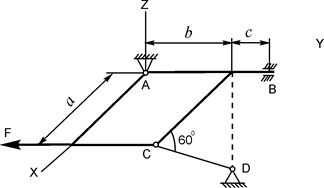
| G = 8 кН; F = 9 кН; a = 3 м; b = 2 м; c = 0,2 м | XA = ? YA = ? ZA = ? XB = ? ZB = ? RC = ? |
Продолжение табл. 1.4
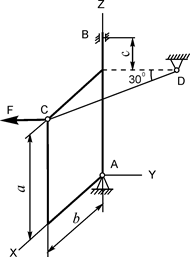
| G = 8 кН; F = 10 кН; a = 3 м; b = 2 м; c = 0,2 м | XA = ? YA = ? ZA = ? YB = ? XB = ? RC = ? | |

| G = 8 кН; F = 4 кН; a = 3 м; b = 2 м; c = 0,2 м | XA = ? YA = ? ZA = ? YB = ? ZB = ? RC = ? | |
| G = 8 кН; F = 3 кН; a = 3 м; b = 2 м; c = 0,2 м | XA = ? YA = ? ZA = ? XB = ? ZB = ? RC = ? |
Продолжение табл. 1.4
| G = 8 кН; F = 2 кН; a = 3 м; b = 2 м; c = 0,2 м | XA = ? YA = ? ZA = ? YB = ? ZB = ? RC = ? | |
| G = 8 кН; F = 2 кН; a = 3 м; b = 2 м; c = 0,2 м | XA = ? YA = ? ZA = ? XB = ? ZB = ? RC = ? | |

| G = 8 кН; F = 5 кН; a = 3 м; b = 2 м; c = 0,2 м | XA = ? ZA = ? ХВ = ? ZB = ? RC = ? RE = ? |
Продолжение табл. 1.4

| G = 8 кН; F = 6 кН; a = 3 м; b = 2 м; c = 0,2 м | YA = ? ZA = ? YB = ? ZB = ? RC = ? RE = ? | ||
| G = 8 кН; F = 4 кН; a = 3 м; b = 2 м; c = 0,2 м | XA = ? ZA = ? XB = ? ZB = ? RC = ? | ||
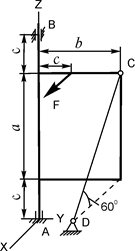
| G = 8 кН; F = 10 кН; a = 3 м; b = 2 м; c = 0,2 м | XA = ? YA = ? ZA = ? XB = ? YB = ? RC = ? | ||
Продолжение табл. 1.4
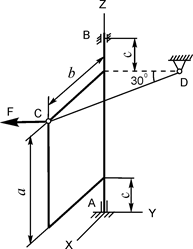
| G = 8 кН; F = 8 кН; a = 3 м; b = 2 м; c = 0,2 м | XA = ? YA = ? ZA = ? XB = ? YB = ? RC = ? | |
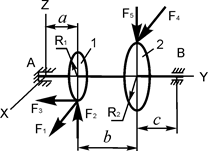
| F1 = 4 кН; F2 =1,2 кН; F3 =0,4 кН; F5 =0,5 кН; R1=0,09 м; R2=0,27 м; a = 0,1 м; b = 0,2 м; с = 0,1 м | XA = ? YA = ? ZA = ? XB = ? ZB = ? F4 = ? | |
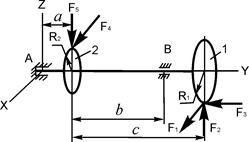
| F1 = 10 кН; F2 = 3 кН; F3 = 1 кН; F5 = 1,5 кН; R1 = 0,05 м; R2 = 0,12 м; a = 0,1 м; b = 0,15 м; с = 0,22 м | XA = ? YA = ? ZA = ? XB = ? ZB = ? F4 = ? | |
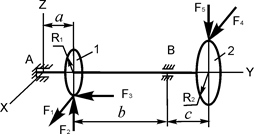
| F1 = 8 кН; F2 = 2,5 кН; F3 = 1 кН; F5 = 2 кН; R1 = 0,2 м; R2 = 0,3 м; a = 0,1 м; b = 0,12 м; с = 0,2 м | XA = ? YA = ? ZA = ? XB = ? ZB = ? F4 = ? |
Продолжение табл. 1.4
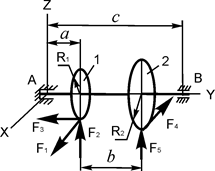
| F1 = 12 кН; F2 = 4 кН; F3 = 1,5 кН; F5 = 2 кН; R1 = 0,1 м; R2 = 0,2 м; a = 0,1 м; b = 0,2 м; с = 0,4 м | XA = ? YA = ? ZA = ? XB = ? ZB = ? F4 = ? | |
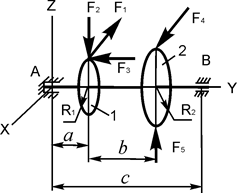
| F1 = 3 кН; F2 = 1 кН; F3 = 0,5 кН; F5 = 1,2 кН; R1 = 0,07 м; R2 = 0,25 м; a = 0,12 м; b = 0,15 м; с = 0,45 м | XA = ? YA = ? ZA = ? XB = ? ZB = ? F4 = ? | |

| F1 = 9 кН; F2 = 3,5 кН; F3 = 2 кН; F5 = 1,25 кН; R1 = 0,06 м; R2 = 0,15 м; a = 0,2 м; b = 0,3 м; с = 0,7 м | XA = ? ZA = ? XB = ? YB = ? ZB = ? F4 = ? | |
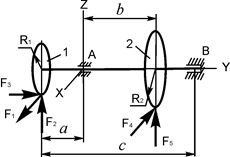
| F1 = 3 кН; F2 = 1 кН; F3 = 0,5 кН; F5 = 2,5 кН; R1 = 0,15 м; R2 = 0,18 м; a = 0,1 м; b = 0,12 м; с = 0,3 м | XA = ? ZA = ? XB = ? YB = ? ZB = ? F4 = ? |
Продолжение табл. 1.4
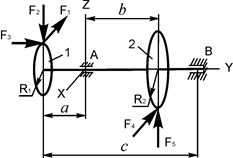
| F1 = 7 кН; F2 = 2,8 кН; F3 = 0,8 кН; F5 = 4 кН; R1 = 0,07 м; R2 = 0,12 м; a = 0,12 м; b = 0,2 м; с = 0,47 м | XA = ? ZA = ? XB = ? YB = ? ZB = ? F4 = ? | |
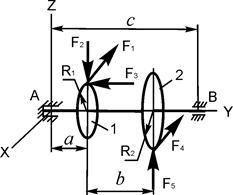
| F1 = 6 кН; F2 = 2 кН; F3 = 0,6 кН; F5 = 2,5 кН; R1 = 0,06 м; R2 = 0,16 м; a = 0,2 м; b = 0,25 м; с = 0,55 м | XA = ? YA = ? ZA = ? XB = ? ZB = ? F4 = ? | |
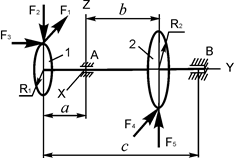
| F1 = 11 кН; F2 = 4 кН; F3 = 2 кН; F5 = 5 кН; R1 = 0,1 м; R2 = 0,2 м; a = 0,1 м; b = 0,12 м; с = 0,3 м | XA = ? ZA = ? XB = ? YB = ? ZB = ? F4 = ? | |
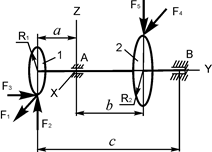
| F1 = 2 кН; F2 = 0,8 кН; F3 = 0,2 кН; F5 = 1 кН; R1 = 0,05 м; R2 = 0,12 м; a = 0,14 м; b = 0,11 м; с = 0,45 м | XA = ? ZA = ? XB = ? YB = ? ZB = ? F4 = ? |
Окончание табл.1.4

| F1 = 8 кН; F2 = 3 кН; F3 = 1,2 кН; F5 = 3,6 кН; R1 = 0,06 м; R2 = 0,15 м; a = 0,1 м; b = 0,2 м; с = 0,55 м | XA = ? ZA = ? XB = ? YB = ? ZB = ? F4 = ? | |

| F1 = 14 кН; F2 = 5 кН; F3 = 2 кН; F5 = 3 кН; R1 = 0,08 м; R2 = 0,12 м; a = 0,12 м; b = 0,24 м; с = 0,5 м | XA = ? ZA = ? XB = ? YB = ? ZB = ? F4 = ? | |
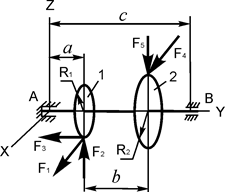
| F1 = 12 кН; F2 = 4 кН; F3 = 1 кН; F5 = 4,8 кН; R1 = 0,1 м; R2 = 0,25 м; a = 0,12 м; b = 0,18м; с = 0,8 м | XA = ? YA = ? ZA = ? XB = ? ZB = ? F4 = ? | |
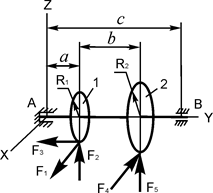
| F1 = 5 кН; F2 = 2 кН; F3 = 0,5 кН; F5 = 1 кН; R1 = 0,12 м; R2 = 0,25 м; a = 0,15 м; b = 0,2 м; с = 0,45 м | XA = ? YA = ? ZA = ? XB = ? ZB = ? F4 = ? |
Пример выполнения курсового задания С 4
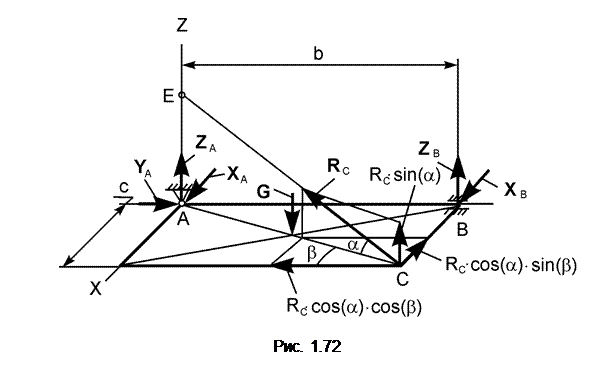
Однородная прямоугольная рама весом 200 Н прикреплена к стене при помощи шарового шарнира А и цилиндрического шарнира в точке В и удерживается в горизонтальном положении верёвкой СЕ, привязанной в точке С рамы и гвоздю Е, вбитому в стену на одной вертикали с точкой А (рис. 1.72). Угол α = 30о.
Определить натяжение верёвки и опорные реакции в точках А и В, если b = с = 1 м.
Решение. Как и ранее, определение реакций внешних связей для рассматриваемой конструкции проводится согласно плану решения задач статики.
1. Выбирается система отсчёта AXYZ, начало которой помещается в шаровый шарнир А.
2. Выделяется тело, равновесие которого рассматривается. В нашем случае таким телом является однородная прямоугольная рама, изображённая на рис. 1.72.
3. К раме в центре её тяжести прикладывается активная сила G – сила тяжести.
4. Согласно аксиоме связей отбрасывают внешние связи (в точке А шаровый шарнир, в точке В цилиндрический шарнир, в точке С нить) и показывают реакции связей – XA, YA, ZA, XB, YB, RC. Для удобства решения реакцию RC нити разложим на составляющие, параллельные координатным осям AX, AY, AZ: RC·sin(α) II AZ; RC·cos(α)·sin(β) II AX; RC·cos(α)·cos(β) II AY. Здесь величина угла β находится из размеров прямоугольной рамы по формуле β = arctg(c/b) = arctg(1/1) = arctg(1) = 45o.
5. Таким образом, на раму действует пространственная произвольная система сил (G, XA, YA, ZA, XB, YB, RC). Поэтому для решения задачи записываются шесть уравнений равновесия.
Σ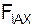 + Σ
+ Σ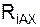 = 0 = – RC·cos(α)·sin(β) + XA + XB = 0; (1)
= 0 = – RC·cos(α)·sin(β) + XA + XB = 0; (1)
Σ + Σ
+ Σ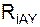 = 0 = YA – RC·cos(α)·cos(β) = 0; (2)
= 0 = YA – RC·cos(α)·cos(β) = 0; (2)
Σ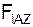 + Σ
+ Σ = 0 = – G + ZA + RC·sin(α) = 0; (3)
= 0 = – G + ZA + RC·sin(α) = 0; (3)
Σ MAX(FiE) + Σ MAX(RiE) = 0
= – G·(b/2) + RC·sin(α)·b + ZB·b = 0; (4)
Σ MAY(FiE) + Σ MAY(RiE) = 0 =
= G·(c/2) – RC·sin(α)·c = 0; (5)
Σ MAZ(FiE) + Σ MAZ(RiE) = 0 = – XB·b = 0. (6)
Полученная система уравнений решается в наиболее удобной последовательности и определяются проекции реакций внешних связей на координатные оси системы отсчёта AXYZ.
Из уравнения (6) имеем XB = 0.
Из уравнения (5) определяется модуль реакции RC:
RC = G/(2·sin(α)) = 200/(2·0,5) = 200 Н.
Из уравнения (4) находится ZB:
ZB = G/2 – RC·sin(α) = 200/2 – 200·0,5 = 0.
Из уравнения (3) вычисляется ZA:
ZA = G – RC·sin(α) = 200 – 200·0,5 = 100 Н.
Из уравнения (2) определяется YA:
YA = RC·cos(α)·cos(β) = 200·0,866·0,707 = 122,452 Н.
Из уравнения (1) находится XA.
XA = – XB + RC·cos(α)·sin(β) = – 0 + 200·0,866·0,707 = 122,452 Н.
Результаты проведенных расчётов помещают в таблицу.
Таблица
| Проекции реакций внешних связей на координатные оси системы отсчёта AXYZ | |||||
| XA, Н | YA, Н | ZA, Н | XB, Н | ZB, Н | RC, Н |
| 122,452 | 122,452 | 100,000 | 0,000 | 0,000 | 200,000 |
Вопросы и задания для самоконтроля
1. Сформулировать определение термина «момент силы F относительно оси OZ».
2. Записать формулы для определения момента силы F относительно координатных осей декартовой системы отсчёта.
3. Сформулировать определение термина «пространственная произвольная система сил».
4. Записать уравнения равновесия пространственной произвольной системы сил.
5. Записать уравнения равновесия для пространственной системы сил, линии действия которых параллельны оси OZ декартовой системы отсчёта.
Сцепление и трение скольжения
Рассмотрим равновесие тела лежащего на горизонтальной шероховатой поверхности…СЛОВАРЬ
ТЕРМИНОВ, ОПРЕДЕЛЕНИЙ, ПОНЯТИЙ
Механика – наука о механическом движении и механическом взаимодействии материальных тел. Теоретическая механика – раздел механики, в котором изучают законы движения механических систем и общие свойства этих…РАЗДЕЛ ВТОРОЙ

КИНЕМАТИКА
Введение в кинематику
Кинематикой называется раздел механики, в котором изучается движение материальных тел в пространстве, вне связи с силами, определяющими это движение.
Механическое движение, т.е. происходящее во времени изменение положения одного тела относительно другого, рассматриваемое в системе отсчёта, которая и связана с этим другим телом.
Система отсчёта может быть как движущейся, так и условно неподвижной. При изучении движений на Земле за неподвижную систему отсчёта (НСО) принимают систему координатных осей, неизменно связанных с Землей. Тело, положение которого по отношению к выбранной системе отсчёта не изменяется, находится в состоянии относительного покоя (по отношению к этой системе отсчёта).
Пространство в механике рассматривается как трёхмерное евклидово пространство. За единицу длины при измерении расстояний принимается метр (м). За единицу времени принимается одна секунда (с). Все кинематические характеристики движения тела (расстояния, скорости, ускорения) рассматриваются как функции времени.
2.2. Координатный способ задания движения точки
Рассматривается движение точки М в неподвижной системе отсчёта OXYZ (рис. 2.1). Единичные векторы (орты) i, j, k показывают положительные направления отсчёта координат X, Y, Z. Движущаяся точка описывает в пространстве некоторую линию, которую называют траекторией движения точки. По виду траектории все движения точки делятся на прямолинейные и криволинейные. Положение точки М в неподвижной системе отсчёта (НСО) определяется тремя координатами X, Y, Z. При движении точки М её координаты изменяются с течением времени. Следовательно, коорди
наты X, Y, Z движущейся точки М являются функциями времени t.
Систему трёх уравнений X = f1(t); Y = f2(t); Z = f3(t) называют уравнениями движения точки в пространстве в декартовых координатах.
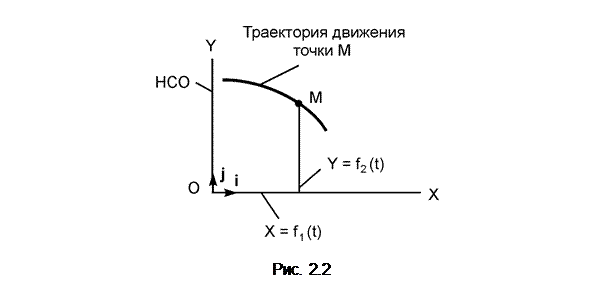
Пример: X = 10·t2 + 1; Y = 7·t3 + t2 + 1; Z = 10·sin(p·t). Действительно, имея эти уравнения, можно для любого момента времени найти значения соответствующих координат X, Y, Z и по ним определить положение точки в пространстве в этот момент времени.
Движение точки М на плоскости (рис. 2.2) определяется двумя уравнениями: X = f1(t); Y = f2(t). Эти выражения называют уравнениями движения точки на плоскости в декартовой системе отсчёта.
Пример. Заданы уравнения движения точки в плоскости OXY. X = 3·t2 + t2 + t; Y = 7·cos(p·t).
Уравнения движения, определяющие координаты точки в любой момент времени, рассматривают как параметрические уравнения траектории точки. При исключении параметра t из уравнений движения получают уравнение траектории точки в координатной форме (Y = f(t)).
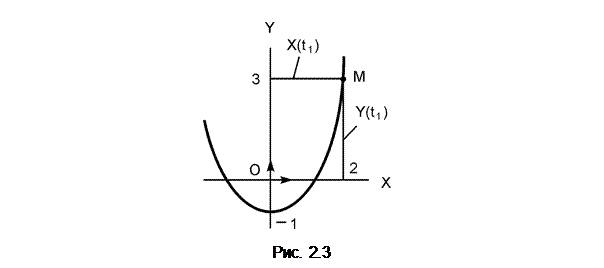
Пример. Заданы уравнения: X = 4·t (см); Y = 16·t2 – 1 (см) движения точки в плоскости OXY. Определить вид траектории движения точки, построить её график и найти положение точки на траектории движения в момент времени t1 = 0,5 с.
Решение. Из уравнения X = 4·t находим t = X/4. Значение времени t подставляем в уравнение Y = 16·t2 – 1. Получаем
Y = 16·(X/4)2 – 1 = X2 – 1.
Выражение Y = X2 – 1 есть уравнение параболы (y= a·x2+b·x+c) с вершиной в точке с координатами (0, – 1). В момент времени t1 = 0,5 с определяем координаты:
X(t1) = 4·t1 = 4·0,5 = 2 см > 0;
Y(t1) = 16·(t1)2 – 1 = 16·(0,5)2 – 1 = 3 см >0.
Показываем положение точки на траектории её движения (рис. 2.3).
Пример. Дано: X = 3·sin(p·t), см (1); Y = 3·cos(p·t), см (2); t1 = 0,25 c. Определить вид траектории движения точки и её положение на траектории движения в момент времени t1.
Решение. Уравнения движения точки представим в следующем виде: (X)2 = (3·sin(p·t))2 (1I); (Y)2 = (3·cos(p·t))2 (2I). Для решения используем тригонометрическую формулу sin2(α) + cos2(α) = 1.
Складывая левые и правые части уравнений (1I) и (2I), получим (X)2 + (Y)2 = 32·(sin2(p·t) + cos2(p·t)) = 32·1 или (X)2 + (Y)2 = 32. Известно, что уравнение (X)2 + (Y)2 = R2 есть уравнение окружности радиусом R с центром в начале координат. Таким образом, точка 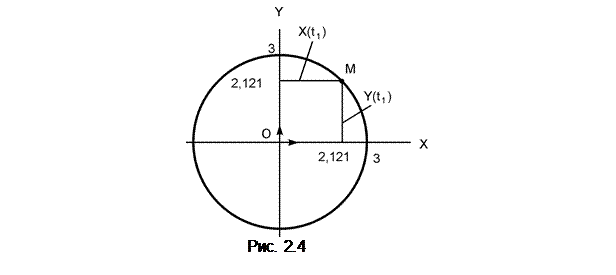
движется по окружности радиусом R = 3 см (рис. 2.4).
Определяем положение точки на траектории движения в момент времени t1.
X(t1) = 3·sin(p·t1) = 3·sin(p·0,25) = 3·0,707 = 2,121 см > 0.
Y(t1) = 3·cos(p·t1) = 3·cos(p·0,25) = 3·0,707 = 2,121 см > 0.
Показываем точку на траектории её движения (см. рис. 2.4).
ВНИМАНИЕ! Если точка не попадает на траекторию её движения, то:
1) неверно определен вид траектории движения;
2) неверно рассчитаны значения координат X(t1), Y(t1).
Прямолинейное движение точки М определяется одним уравнением движения X = f(t).
Пример. Дано: X = 10·t2 + sin(2·p·t) + 3, см (рис. 2.5).
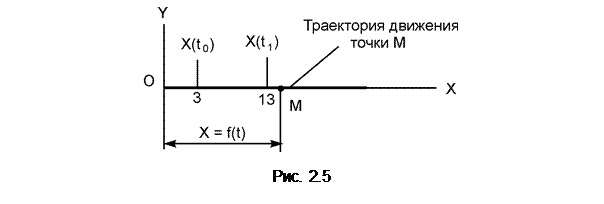
Определить положение точки на траектории движения в начальный момент времени t0 = 0 и в момент времени t1 = 1 c.
Решение.
X(t0) = 10·(t0)2 + sin(2·p·t0) + 3 = 10·02 + sin(2·p·0) + 3 = 3 см > 0.
X(t1) = 10·(t1)2 + sin(2·p·t1) + 3 = 10·12 + sin(2·p·1) + 3 = 13 см > 0.
Значения координат X(t0), X(t1) наносим на рис. 2.5.
Скорость точки
Скорость – векторная величина, характеризующая быстроту и направление движения…Ускорение точки
Ускорение – векторная величина, характеризующая быстроту изменения величины и…Естественный способ задания
Движения точки
Естественный способ задания движения точки…Естественные координатные оси
Точка перемещается в пространстве по заданному уравнению движения S = f(t)… Проведём в точке М кривой АВ соприкасающуюся плоскость, нормальную плоскость, перпендикулярную соприкасающейся…Скорость точки
Скорость точки при естественном способе задания движения определяется по… V = τ·(dS/dt) = τ·,Ускорение точки
Ускорение а точки всегда направлено в сторону вогнутости траектории движения,… a = аoτ + аon ,Классификация движения точки
по ускорениям её движения
Случай 1: аon = 0; аoτ = 0 – точка движется равномерно и прямолинейно.
Случай 2: аon ≠ 0; аoτ = 0 = const – точка движется равномерно по криволинейной траектории.
Случай 3: аon = 0; аoτ ≠ 0 – точка движется не равномерно по прямой линии.
Случай 4: аon ≠ 0; аoτ ≠ 0 – точка совершает неравномерное криволинейное движение.
Случай 5: если, непрерывно изменяясь, в некоторый момент времени аoτ = 0, то в этот момент скорость V достигает экстремального значения.
Связь координатного и естественного
Способов задания движения точки
Рассматривается прямолинейное движение точки при естественном и координатном способах задания движения точки (рис. 2.15).
Согласно рис. 2.15 уравнения прямолинейного равнопеременного движения при естественном и координатном способах задания движения точки по существу не отличаются друг от друга.
 |
Естественный способ задания движения точки:
 = const ≠ 0;
= const ≠ 0;
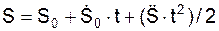 .
.
Координатный способ задания движения точки:
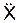 = const ≠ 0;
= const ≠ 0;
 .
.
Таким образом, при прямолинейном равнопеременном движении точки уравнения X = f(t), S = f(t) в координатном и естественном способах задания имеют один и тот же вид.
Векторный способ задания движения точки
Положение точки в пространстве однозначно определяется заданием радиус-вектора r, проведённого из некоторого неподвижного центра О в данную точку М (рис. 2.16).
Для определения движения точки нужно знать, как изменяется с течением времени радиус-вектор, т. е. должна быть задана вектор-функция rаргумента t.
r = r(t).
Это выражение называют уравнением движенияпривекторном способе задания движения точки.

Траектория движения точки является геометрическим местом концов радиус-вектора r. Иногда траекторию движения точки называют годографомрадиус-вектораr.
Векторный способ задания движения точки, как правило, используется при доказательстве теорем, так как он упрощает многие выводы и иногда подчёркивает физическую сущность явления.
Вектор V скорости точки направлен по касательной к траектории в сторону движения точки. Вектор скорости точки в данный момент равен производной от радиус-вектора точки по времени:
V = dr/dt = 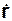 ,
,
где (·) – символ однократного дифференцирования функции r = r(t) по времени.
Ускорение а направлено в сторону вогнутости траектории движения точки. Вектор ускорения точки в данный момент времени равен первой производной от скорости V или второй производной от радиус-вектора r = r(t) точки по времени:
a = dV/dt = d2r/dt2 = 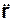 ,
,
где (··) – символ двойного дифференцирования функции r = r(t) по времени.
Если поместить начало неподвижной системы отсчёта OXYZ в точку О (точка О – полюс радиус-вектора r = r(t)), то можно связать координатный и векторный способы задания движения точки. Так как единичные векторы I, j, k системы отсчёта OXYZ постоянны, то справедливы следующие равенства:
r = i·X + j·Y + k·Z;
V = 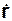 = i·
= i·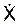 + j·
+ j·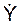 + k·
+ k·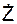 ;
;
a= 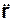 = i·
= i· + j·
+ j·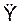 + k·
+ k·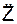 .
.
Варианты курсового задания К 1
«Определение скорости и ускорения точки
по заданным уравнениям её движения»
Для закрепления теоретического материала рекомендуется выполнить курсовое задание К 1.
По заданным уравнениям движения точки М (табл. 2.1) установить вид её траектории и для момента времени t1 найти положение точки на траектории, её скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории.
Таблица 2.1
| Номер варианта | Уравнения движения | t1, c | |
| X = X(t), см | Y = Y(t), см | ||
| – 2·t2 + 3 | – 5·t | 0,5 | |
| 4·cos2·(p·t/3) + 2 | 4·sin2·(p·t/3) | ||
| – cos(p·t2/3) + 3 | sin(p·t2/3) – 1 | ||
| 4·t + 4 | – 4·(t + 1) | ||
| 2·sin(p·t/3) | – 3·cos(p·t/3) + 4 | ||
| 3·t2 + 2 | – 4·t | 0,5 | |
| 3·t2 – t + 1 | 5·t2 – 5·t/3 – 2 | ||
| 7·sin(p·t2/6) + 3 | 2 – 7·cos(p·t2/6) | ||
| – 3/(t + 2) | 3·t + 6 | ||
| – 4·cos(p·t/3) | – 2·sin(p·t/3) – 3 | ||
| – 4·t2 + 1 | – 3·t | 0,5 | |
| 5·sin2·(p·t/6) | – 5·cos2·(p·t/6) – 3 | ||
| 5·cos(p·t2/3) | – 5·sin(p·t2/3) | ||
| – 2·t – 2 | – 2/(t + 1) | ||
| 4·cos(p·t/3) | – 3·sin(p·t/3) | ||
| 3·t | 4·t2 + 1 | 0,5 | |
| 7·sin2·(p·t/6) – 5 | – 7·cos2·(p·t/6) | ||
| 1 + 3·cos(p·t2/3) | 3·sin(p·t2/3) + 3 | ||
| – 5t2 – 4 | 3t | ||
| 2 – 3·t – 6·t2 | 3 – 3·t/2 – 3·t2 |
Окончание табл. 2.1
| 6·sin(p·t2/6) – 2 | 6·cos(p·t2/6) + 3 | ||
| 7·t2 – 3 | 5·t | 0,25 | |
| 3 – 3·t2 + t | 4 – 5·t2 + 5·t/3 | ||
| – 4·cos(p·t/3) – 1 | – 4·sin(p·t/3) | ||
| – 6·t | – 2·t2 – 4 | ||
| 8·cos2·(p·t/6) + 2 | – 8·sin2·(p·t/6) – 7 | ||
| – 3 – 9·sin(p·t2/6) | – 9·cos(p·t2/6) + 5 | ||
| – 4·t2 + 1 | – 3·t | ||
| 5·t2 + 5·t/3 – 3 | 3·t2 + t + 3 | ||
| 2·cos(p·t2/3) – 2 | – 2·sin(p·t2/3) + 3 |
Пример выполнения курсового задания К 1
Исходные данные: X = X(t) = 2·cos(p·t2/3) – 2; см. (1)
Y = Y(t) = – 2·sin(p·t2/3) + 3; см. (2)
t1 = 1 c.
По заданным уравнениям движения точки на плоскости определить кинематические характеристики в момент времени t1.
Решение.
1. Для определения траектории движения точки уравнения (1) и (2) связываются через параметр t. Уравнения (1) и (2) выразим в следующем виде:
X + 2 = 2·cos(p·t2/3); (1I)
Y – 3 = – 2·sin(p·t2/3). (2I)
Возведём в квадрат левые и правые части уравнений (1I), (2I) и сложим их.
(X + 2)2 = (2·cos(p·t2/3))2; (1II)
+
(Y – 3)2 = (– 2·sin(p·t2/3))2. (2II)
После сложения уравнений (1II), (2II) получим
(X + 2)2 + (Y – 3)2 = (2·cos(p·t2/3))2 + (– 2·sin(p·t2/3))2 =
= 22·((cos(p·t2/3))2 + (sin(p·t2/3)))2 = 22·1 = 22.
При преобразованиях использована тригонометрическая формула sin2(α) + cos2(α) = 1. Полученное уравнение
(X + 2)2 + (Y– 3)2 = 22
есть уравнение окружности (x – a)2+(y – b)2 = r2 c центром в точке с координатами (a, b). Построим график траектории движения точки (рис. 2.17).

2. Определение положения точки на траектории её движения в момент времени (t1).
В уравнения (1) и (2) подставляем время t1.
X(t1) = 2·cos(p·(t1)2/3) – 2 = 2·cos(p·(1)2/3) – 2 =
= 2·0,5 – 2 = 1,000 см < 0.
Y(t1) = – 2·sin(p·(t1)2/3) + 3 = – 2·sin(p·(1)2/3) + 3 =
= – 2·0,866 + 3 = 1,270 см > 0.
Точку с координатами (–1, 1,270) показываем на траектории её движения.
ВНИМАНИЕ!
Если точка не попала на траекторию её движения, то:
1) неверно определена траектория движения;
2) неверно подсчитаны значения координат точки.
3. Определение скорости точки.
Для определения скорости точки найдем производные по времени от соответствующих уравнений её движения:
 = 2·(– sin(p·t2/3)·(2·p·t/3)) = (– 4·p/3)·(sin(p·t2/3))·t;
= 2·(– sin(p·t2/3)·(2·p·t/3)) = (– 4·p/3)·(sin(p·t2/3))·t;
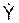 = – 2·(cos(p·t2/3)·(2·p·t/3)) = (– 4·p/3)·(cos(p·t2/3))·t.
= – 2·(cos(p·t2/3)·(2·p·t/3)) = (– 4·p/3)·(cos(p·t2/3))·t.
Вычислим значения проекций  ,
, 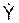 скорости на оси OX и OY в момент времени t1:
скорости на оси OX и OY в момент времени t1:
 (t1) = (– 4·p/3)·(sin(p·(t1)2/3))·t1 =
(t1) = (– 4·p/3)·(sin(p·(t1)2/3))·t1 =
=(– 4·3,14/3)·sin(p·12/3)·1 = – 3,625 см/с < 0;
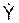 (t1) = (– 4·p/3)·(cos(p·(t1)2/3))·t1 =
(t1) = (– 4·p/3)·(cos(p·(t1)2/3))·t1 =
=(– 4·3,14/3)·cos(p·12/3)·1 = – 2,093 см/с < 0.
Так как  (t1) и
(t1) и 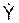 (t1) меньше нуля, то векторы VOX, VOY направлены в стороны, противоположные векторам i, j. В выбранном масштабе наносим векторы VOX, VOY на чертёж (рис. 2.17).
(t1) меньше нуля, то векторы VOX, VOY направлены в стороны, противоположные векторам i, j. В выбранном масштабе наносим векторы VOX, VOY на чертёж (рис. 2.17).
На векторах VOX, VOY строим вектор Vпо правилу параллелограмма. Вектор скорости Vнаправлен по касательной к траектории движения точки.
ВНИМАНИЕ!
Если вектор Vнаправлен не по касательной к траектории движения, то:
1) неверно взяты производные  ,
, 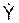 ;
;
2) неверно вычислены значения  (t1),
(t1), 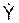 (t1).
(t1).
Вычисляется модуль V скорости V в момент времени (t1) по формуле
 =
=
= 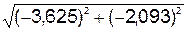 = 4,186 см/с.
= 4,186 см/с.
В ряде вариантов можно определить модуль скорости по формуле
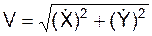 = =
= =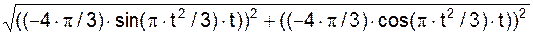 =
=
= 4·p·t/3.
V(t1) = 4·p·t1/3 = 4·3,14·1/3 = 4,186 см/с.
4. Определение ускорения точки.
Находятся производные по времени от проекций  ,
, 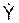 скорости на координатные оси OX, OY.
скорости на координатные оси OX, OY.
Так как проекция  скорости на ось ОХ представляет собой произведение двух переменных ((– 4·p/3)·sin(p·t2/3) и t), то по правилу дифференцирования произведения получим
скорости на ось ОХ представляет собой произведение двух переменных ((– 4·p/3)·sin(p·t2/3) и t), то по правилу дифференцирования произведения получим
 (– 8·p2/9)·cos(p·t2/3)·t2 – (4·p/3)·sin(p·t2/3).
(– 8·p2/9)·cos(p·t2/3)·t2 – (4·p/3)·sin(p·t2/3).
Аналогично
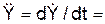 (8·p2/9)·sin(p·t2/3)·t2 – (4·p/3)·cos(p·t2/3).
(8·p2/9)·sin(p·t2/3)·t2 – (4·p/3)·cos(p·t2/3).
Определим 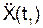 и
и  , подставляя в последние формулы значение времени t1. Произведя расчеты, получим:
, подставляя в последние формулы значение времени t1. Произведя расчеты, получим:
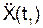 = – 8,020 см/с2;
= – 8,020 см/с2;  = 5,510 см/с2.
= 5,510 см/с2.
Так как 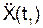 <0, то вектор aOX направлен в сторону, противоположную орту i. Вектор aOY направлен в ту же сторону, что и вектор j, так как
<0, то вектор aOX направлен в сторону, противоположную орту i. Вектор aOY направлен в ту же сторону, что и вектор j, так как  >0. На векторах aOX и aOY строим вектор ускорения a. Вектор ускорения a всегда направлен в сторону вогнутости траектории.
>0. На векторах aOX и aOY строим вектор ускорения a. Вектор ускорения a всегда направлен в сторону вогнутости траектории.
ВНИМАНИЕ!
Если ускорение aнаправлено не в сторону вогнутости траектории движения, то:
1) неверно взяты производные 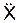 ,
, 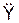 ;
;
2) неверно вычислены значения 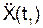 ,
,  .
.
Определяется модуль ускорения по формуле
a(t1) =  =
= 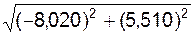 = 9,730 см/с2.
= 9,730 см/с2.
5. Определение касательного и нормального ускорений.
На рис. 2.17 наносим подвижную систему отсчёта (ПСО). Разложим полное ускорение a на касательное аoτ и нормальное аon ускорения. Так как касательное ускорение аoτ совпадает с направлением скорости V, то точка движется ускоренно. Модуль аoτ касательного ускорения в момент времени t1 находится по формуле
аoτ(t1) = |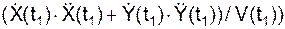 | = |
| = | (t1)| =
(t1)| =
= |((– 3,625)·(– 8,020) + (– 2,099)·5,510)/4,186| = 4,186 см/с2.
Касательное ускорение характеризует быстроту изменения величины скорости, поэтому его проекция на касательную может быть определена по формуле
 = dV/dt = d(4pt/3)/dt = 4p/3 = 4·3,14/3 = 4,186 см/с2 = const > 0.
= dV/dt = d(4pt/3)/dt = 4p/3 = 4·3,14/3 = 4,186 см/с2 = const > 0.
Так как  = const и направления аoτ и V совпадают, то точка движется по окружности равноускоренно. аoτ =
= const и направления аoτ и V совпадают, то точка движется по окружности равноускоренно. аoτ =  = const.
= const.
Модуль нормального ускорения находится по формуле
аon(t1) = 
 =
=
= 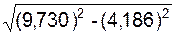 = 8,780 см/с2.
= 8,780 см/с2.
Из формулы аon = V2/ρ определяется радиус кривизны траектории движения ρ(t1) = V2(t1)/(аon(t1)) = (4,186)2/8,780 = 2,0 см. Таким образом, радиус кривизны траектории движения равен радиусу окружности, по которому перемещается точка.
Результаты вычислений заносятся в таблицу.
Таблица
| X(t1), см | Y(t1), см | 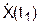 , см/с , см/с
| 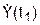 , см/с , см/с
| 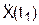 , см/с2 , см/с2
| 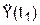 , см/с2 , см/с2
|
| – 1,00 | 1,27 | – 3,63 | – 2,09 | – 8,02 | 5,51 |
Окончание таблицы
| V(t1), см/с | а(t1), см/с2 | аoτ(t1), см/с2 | аon(t1) , см/с2 | ρ(t1), см | |
| 4,19 | 9,73 | 4,20 | 8,78 | 2,00 |
Вопросы и задания для самоконтроля
1. Сформулировать определение термина «кинематика».
2. Сформулировать определение термина «механическое движение».
3. Записать уравнения движения точки в декартовой системе отсчёта (точка движется в пространстве).
4. Записать уравнения движения точки в декартовой системе отсчёта (точка движется в горизонтальной плоскости).
5. Записать уравнения движения точки в декартовой системе отсчёта (точка движется параллельно оси ОХ).
6. Записать уравнение траектории движения точки в декартовой системе отсчёта (точка движется в вертикальной плоскости OYZ).
7. Сформулировать определение термина «скорость».
8. Записать формулу для определения скорости точки через компоненты скорости в декартовой системе отсчёта.
9.Записать формулы для определения проекций скорости на координатные оси в декартовой системе отсчёта.
10. Записать формулу для определения модуля скорости через её проекции в декартовой системе отсчёта.
11. Записать формулы для определения направляющих косинусов при ориентации скорости в декартовой системе отсчёта.
12. Как направлена скорость точки по отношению к траектории её движения?
13. Сформулировать определение термина «ускорение».
14. Куда направлено ускорение точки по отношению к криволинейной траектории её движения?
15. Записать формулу для определения ускорения точки через компоненты ускорения в декартовой системе отсчёта.
16. Записать формулы для определения проекций ускорения на координатные оси в декартовой системе отсчёта.
17. Записать формулу для определения модуля ускорения через его проекции в декартовой системе отсчёта.
18. Записать формулы для определения направляющих косинусов при ориентации ускорения в декартовой системе отсчёта.
19. Записать уравнение равнопеременного прямолинейного движения точки в декартовой системе отсчёта.
20. Записать формулу равномерного прямолинейного движения точки в декартовой системе отсчёта.
21. Записать уравнение движения точки в естественных координатах.
22. Записать формулу для определения вектора скорости точки в естественных координатах.
23. При каком условии точка движется в сторону увеличения дуговой координаты?
24. При каком условии точка движется в сторону уменьшения дуговой координаты?
25. Записать формулу для определения модуля скорости в естественных координатах.
26. Записать формулу для определения вектора ускорения в естественных координатах.
27. Сформулировать определение термина «касательное ускорение».
28. Сформулировать определение термина «нормальное ускорение».
29. Записать формулу для определения вектора касательного ускорения.
30. Записать формулу для определения вектора нормального ускорения.
31. Записать формулу для определения модуля ускорения точки при естественном способе задания движения точки.
32. Записать формулу для определения модуля касательного ускорения с использованием проекций скорости и ускорения на координатные оси декартовой системы отсчёта.
33. Как движется точка, если проекции её скорости и ускорения на касательную совпадают по знакам?
34. Как движется точка, если проекции её скорости и ускорения на касательную не совпадают по знакам?
35. Что характеризует касательное ускорение?
36. Что характеризует нормальное ускорение?
37. Чему равен радиус кривизны траектории при прямолинейном движении точки?
38. При каких условиях происходит прямолинейное движение точки?
39. При каких условиях происходит равномерное криволинейное движение?
40. При каких условиях происходит неравномерное криволинейное движение?
41. Записать уравнение движения точки при векторном способе задания её движения.
42. Записать формулу для определения скорости точки при векторном способе задания её движения.
43. Записать формулу для определения ускорения точки при задании её движения векторным способом.
44. Записать уравнение равнопеременного движения точки в естественных координатах.
45. Записать уравнение равномерного движения точки в естественных координатах.
2.14. Поступательное движение твёрдого тела
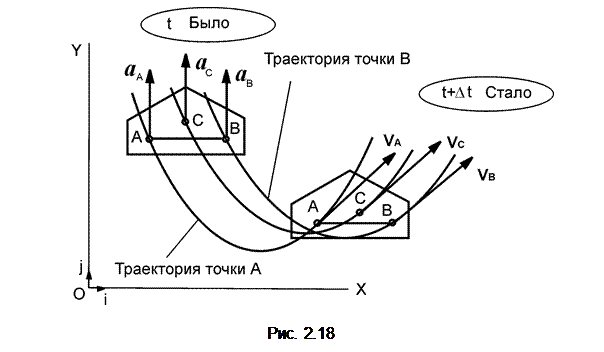 Поступательным движением твёрдого тела называется такое движение, при котором любая прямая линия, проведенная на теле, остается во всё время движения тела параллельной своему начальному положению (рис. 2.18).
Поступательным движением твёрдого тела называется такое движение, при котором любая прямая линия, проведенная на теле, остается во всё время движения тела параллельной своему начальному положению (рис. 2.18).
При поступательном движении траектории всех точек тела одинаковы (при наложении друг на друга траектории движения точек А, В, С совпадают), а скорости и ускорения всех точек геометрически равны:
VA = VB = VC = …; aA = aB = aС = ….
Эти свойства позволяют свести изучение поступательного движения тела к изучению движения его отдельной точки, т. е. к задаче кинематики точки. За такую точку, как правило, выбирают центр тяжести (центр масс) тела.
Рассматривается поступательное движение тела, при котором все его точки перемещаются параллельно неподвижной плоскости OXY (рис. 2.19).
Выражения XC = f1(t), YC = f2(t), описывающие движение центра С тяжести тела называют уравнениями поступательного движения твёрдого тела на плоскости.
Уравнений поступательного движения в пространстве три, а при прямолинейном поступательном движении – одно.

Таким образом, для тела при его поступательном движении имеем следующие выражения:
– уравнения поступательного движения тела в пространстве:
XC = f1(t), YC = f2(t), ZC = f3(t);
– уравнения поступательного движения тела параллельно плоскости OXY:
XC = f1(t), YC = f2(t);
– уравнение поступательного движения тела параллельно координатной оси ОХ
XC = f1(t).
Если заданы уравнения поступательного движения тела, то несложно определить скорость VC и ускорение aС центра масс, а следовательно, и скорость, и ускорение любой точки этого тела по следующим формулам.
Проекции 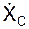 ,
, 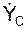 ,
, 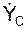 скорости VC центра масс на координатные оси:
скорости VC центра масс на координатные оси:
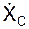 = dXC/dt;
= dXC/dt; 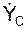 = dYC/dt;
= dYC/dt; 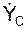 = dZC/dt.
= dZC/dt.
Модуль VC скорости центра масс
VC = 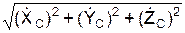 .
.
Направляющие косинусы:
cos(VC, i) = 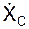 / VC; cos(VC, j) =
/ VC; cos(VC, j) = 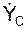 / VC;
/ VC;
cos(VC, k) = 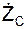 / VC.
/ VC.
Проекции 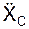 ,
, 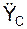 ,
, 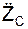 ускорения центра масс на координатные оси:
ускорения центра масс на координатные оси:
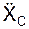 =
= 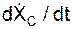 = d2XC/dt2;
= d2XC/dt2;
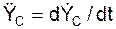 = d2YC/dt2;
= d2YC/dt2;
 = d2ZC/dt2.
= d2ZC/dt2.
Модуль ускорения центра масс
aС =  .
.
Направляющие косинусы:
cos(aС, i) = 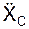 / aС; cos(aС, j) =
/ aС; cos(aС, j) =  / aС; cos(aС, k) =
/ aС; cos(aС, k) =  / aС.
/ aС.
Таким образом, зная уравнения поступательного движения тела, можно найти следующие кинематические характеристики:
1) траекторию движения;
2) положение тела на траектории движения в любой момент времени;
3) скорость любой точки и ориентацию вектора этой скорости в пространстве;
4) ускорение любой точки и ориентацию вектора этого ускорения в пространстве в любой момент времени.
Поступательное движение является простейшим видом движения твёрдого тела.
2.15. Вращательное движение твёрдого тела
Вращательным движением твёрдого тела называется такое его движение, при котором все точки, находящиеся на прямой, неизменно связанной с телом и называемой осью вращения, остаются неподвижными.
Таким образом, при вращательном движении твёрдого тела ось вращения всегда неподвижна (рис. 2.20).
При этом движении все остальные точки тела движутся в плоскостях, перпендикулярных оси вращения, и описывают окружности, центры которых лежат на неподвижной оси вращения.
При вращении тела угол его поворота φ изменяется в зависимости от времени t:
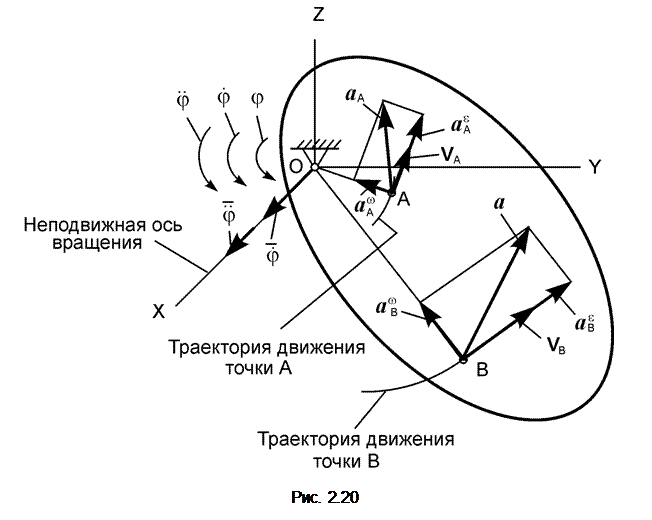
φ = f(t).
Эту аналитическую зависимость (φ = f(t)) называют уравнением вращательного движения твёрдого тела. Она полностью определяет положение тела в пространстве в любой момент времени.
На рис. 2.20 показано направление положительного отсчёта угла поворота φ. Угол φ измеряется в рад.
Пусть, например, задано уравнение вращательного движения
φ = p·t2 + 2·p·t + p/4 (рад).
Величина, характеризующая быстроту изменения угла поворота φ с течением времени, называется угловой скоростью и обозначается  .
.
Угловая скорость  равна производной по времени от уравнения φ = f(t) вращательного движения твердого тела:
равна производной по времени от уравнения φ = f(t) вращательного движения твердого тела:
 = dφ/dt.
= dφ/dt.
Угловую скорость принято обозначать  , где (·) – символ дифференцирования функции φ = f(t) по времени.
, где (·) – символ дифференцирования функции φ = f(t) по времени.
Для приведенного примера уравнения вращательного движения тела φ = pt2 + 2pt + p/4 имеем  = dφ/dt = 2pt + 2p.
= dφ/dt = 2pt + 2p.
Угловая скорость измеряется в рад/с.
Если  > 0, то угол поворота φ увеличивается, т. е. вращение тела происходит в положительном направлении отсчёта угла поворота.
> 0, то угол поворота φ увеличивается, т. е. вращение тела происходит в положительном направлении отсчёта угла поворота.
Если 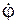 < 0, то угол поворота φ уменьшается, т. е. тело вращается в сторону отрицательного направления отсчёта угла φ.
< 0, то угол поворота φ уменьшается, т. е. тело вращается в сторону отрицательного направления отсчёта угла φ.
Если 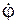 при переходе значения
при переходе значения  = 0, непрерывно изменяясь, меняет знак, то угол поворота φ в этот момент времени достигает максимума или минимума, т. е. изменяется направление вращения тела.
= 0, непрерывно изменяясь, меняет знак, то угол поворота φ в этот момент времени достигает максимума или минимума, т. е. изменяется направление вращения тела.
Таким образом, знак производной  указывает направление вращения тела.
указывает направление вращения тела.
Модуль угловой скорости обозначают символом ω. Отсюда имеем ω = I I.
I.
Величина, характеризующая быстроту изменения угловой скорости с течением времени, называется угловым ускорением тела.
Угловое ускорение принято обозначать 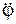 , где (··) – символ двойного дифференцирования функции φ = f(t) по времени.
, где (··) – символ двойного дифференцирования функции φ = f(t) по времени.
Угловое ускорение 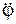 равно второй производной по времени от угла поворота φ или первой производной по времени от угловой скорости
равно второй производной по времени от угла поворота φ или первой производной по времени от угловой скорости  :
:
 = d2φ/dt2 = d
= d2φ/dt2 = d /dt.
/dt.
Для рассматриваемого случая имеем
 = d
= d /dt = d(2·p·t + 2·p)/dt = 2·p рад/с2 = const > 0.
/dt = d(2·p·t + 2·p)/dt = 2·p рад/с2 = const > 0.
Угловое ускорение  имеет размерность рад/с2. Модуль углового ускорения обозначают символом ε. Исходя из этого, имеем ε = I
имеет размерность рад/с2. Модуль углового ускорения обозначают символом ε. Исходя из этого, имеем ε = I I.
I.
Если знаки  и
и  совпадают, то вращение тела происходит ускоренно:
совпадают, то вращение тела происходит ускоренно:
1)  > 0 и
> 0 и  > 0 – происходит ускоренное вращение тела, величина угла φ возрастает;
> 0 – происходит ускоренное вращение тела, величина угла φ возрастает;
2)  < 0 и
< 0 и  < 0 – величина угла поворота φ ускоренно уменьшается.
< 0 – величина угла поворота φ ускоренно уменьшается.
Если знаки  и
и  не совпадают, то происходит замедленное вращение тела:
не совпадают, то происходит замедленное вращение тела:
1)  > 0 и
> 0 и  < 0 – угол поворота φ возрастает замедленно;
< 0 – угол поворота φ возрастает замедленно;
2)  < 0 и
< 0 и  > 0 – величина угла поворота φ замедленно уменьшается.
> 0 – величина угла поворота φ замедленно уменьшается.
Если угловое ускорение  = 0 = const, то происходит равномерное вращение тела, при котором угловая скорость
= 0 = const, то происходит равномерное вращение тела, при котором угловая скорость  постоянна. Уравнение равномерного вращения имеет вид
постоянна. Уравнение равномерного вращения имеет вид
φ = f(t) = φ0 +  ·t.
·t.
Если начальный угол поворота φ0 = 0, то φ = f(t) =  ·t. Из уравнения равномерного вращения имеем
·t. Из уравнения равномерного вращения имеем  = (φ – φ0)/t, т. е. угловая скорость равномерного вращения тела равна отношению угла поворота за некоторый промежуток времени к этому промежутку времени.
= (φ – φ0)/t, т. е. угловая скорость равномерного вращения тела равна отношению угла поворота за некоторый промежуток времени к этому промежутку времени.
Число оборотов, совершаемых вращающимся телом за единицу времени (обычно за минуту), называется частотой вращения и обозначается n (об/мин). Так как один оборот равен 2·p радиан, то зависимость между модулем ω угловой скорости  (рад/с) и частотой вращения имеет вид
(рад/с) и частотой вращения имеет вид
ω = 2·p·n/60 = p·n/30.
Вращение тела, при котором угловое ускорение постоянно и не равно нулю ( = C1 = const ≠ 0), называют равнопеременным вращением. При этом если абсолютная величина угловой скорости увеличивается, вращение называют равноускоренным, а если уменьшается – равнозамедленным. Уравнение равнопеременного вращения имеет вид
= C1 = const ≠ 0), называют равнопеременным вращением. При этом если абсолютная величина угловой скорости увеличивается, вращение называют равноускоренным, а если уменьшается – равнозамедленным. Уравнение равнопеременного вращения имеет вид
φ = φ(t) = φ0 +  ·t + (
·t + ( ·t2)/2.
·t2)/2.
При дифференцировании этого уравнения получим угловую скорость
 = dφ/dt =
= dφ/dt =  +
+  ·t.
·t.
Угловая скорость  и угловое ускорение
и угловое ускорение  являются векторными величинами и обозначаются символами
являются векторными величинами и обозначаются символами  ,
,  . Условимся откладывать вектор угловой скорости
. Условимся откладывать вектор угловой скорости  от любой точки оси вращения, направляя его по этой оси так, чтобы, смотря навстречу этому вектору, видеть вращение тела, происходящим в сторону, противоположную вращению часовой стрелки (рис. 2.21).
от любой точки оси вращения, направляя его по этой оси так, чтобы, смотря навстречу этому вектору, видеть вращение тела, происходящим в сторону, противоположную вращению часовой стрелки (рис. 2.21).
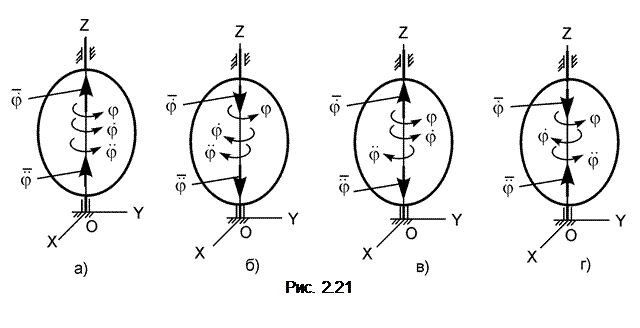
Принятое правило обусловлено применением правой системы отсчёта, которой соответствует положительное направление вращения в сторону, противоположную вращению часовой стрелки.
Вектор углового ускорения 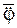 характеризует изменение вектора угловой скорости
характеризует изменение вектора угловой скорости 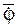 в зависимости от времени, т. е. он должен быть равен производной от вектора угловой скорости по времени:
в зависимости от времени, т. е. он должен быть равен производной от вектора угловой скорости по времени:
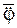 = d
= d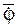 /dt.
/dt.
Направление вектора углового ускорения 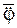 совпадает с направлением вектора
совпадает с направлением вектора 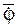 при ускоренном вращении и противоположно ему при замедленном. Согласно рис. 2.21 тело совершает следующие вращения:
при ускоренном вращении и противоположно ему при замедленном. Согласно рис. 2.21 тело совершает следующие вращения:
– ускоренное вращение, угол φ увеличивается (рис. 2.21, а);
– ускоренное вращение, угол φ уменьшается (рис. 2.21, б);
– замедленное вращение, угол φ растет (рис. 2.21, в);
– замедленное вращение, угол φ уменьшается (рис. 2.21, г).
При вращательном движении (см. рис. 2.20) все точки тела описывают окружности с центрами на оси вращения. Как известно, скорости точек направлены по касательной к траектории движения. При вращательном движении скорость точки равна произведению модуля ω угловой скорости  тела на кратчайшее расстояние от точки до оси вращения.
тела на кратчайшее расстояние от точки до оси вращения.
VA = ω·AO; VA ┴ AO; VB = ω·BO; VB ┴ BO.
Из теории кинематики точки известно, что её ускорение направлено в сторону вогнутости траектории. Ускорения точек А, В и т. д. при вращательном движении тела раскладывают на составляющие по касательной и главной нормали к траектории движения;
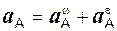 ;
;
 ,
,
где  ,
, 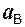 – соответственно векторы ускорений точек А и В тела;
– соответственно векторы ускорений точек А и В тела; 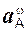 ,
,  – соответственно векторы центростремительных ускорений точек А и В;
– соответственно векторы центростремительных ускорений точек А и В;  ,
, 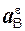 – векторы вращательных ускорений точек А и В.
– векторы вращательных ускорений точек А и В.
Модули центростремительных, вращательных и полных ускорений точек тела находят по формулам:
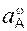 = ω2·АО;
= ω2·АО; 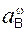 = ω2·ВО;
= ω2·ВО;
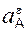 = ε·АО;
= ε·АО; 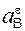 = ε·ВО;
= ε·ВО;
 ;
;
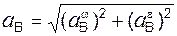 .
.
Модуль центростремительного ускорения точки тела равен произведению квадрата модуля угловой скорости на кратчайшее расстояние от точки до оси вращения.
Модуль вращательного ускорения точки тела равен произведению модуля углового ускорения на кратчайшее расстояние от точки до оси вращения.
На рис. 2.22 и 2.23 представлены варианты механизмов с клиноременной передачей вращательного движения.
Условием безаварийной работы передаточного механизма является одинаковая скорость в точке контакта звеньев этого механизма. Так как участок АВ ремня совершает поступательное движение, то скорости точек А и В равны: VA = VB. Так как точка А принадлежит телу 1, то VA = ω1·R1, где ω1 – модуль угловой скорости 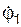 тела 1. Точка В принадлежит телу 2, поэтому VB = ω2·R2, где ω2 – модуль угловой скорости
тела 1. Точка В принадлежит телу 2, поэтому VB = ω2·R2, где ω2 – модуль угловой скорости 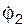 тела 2.
тела 2.
Приравнивая модули скоростей точек А и В, получим:
VA = ω1·R1 = VB = ω2·R2; i = ω1/ω2 = R2/R1 = d2/d1 = n2/n1,
где i – передаточное отношение механизма; R1, R2, d1, d2, n1, n2 – соответственно радиусы, диаметры и частоты вращений колёс, находящихся во вращательном движении.
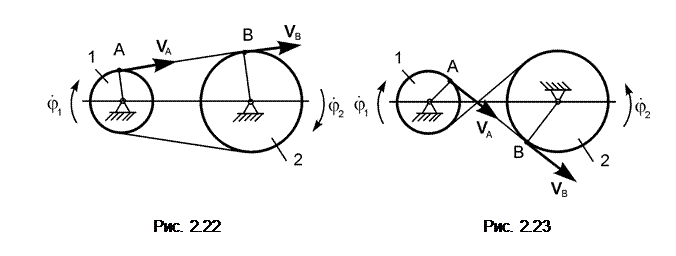

Существует ряд технических решений, в которых применяется серия колёс с неподвижными осями вращений (рис. 2.24).
Нетрудно заметить, что модули скоростей точек K, L, M в рассматриваемом механизме равны. Тогда VK = VL = VM или через модули ω1 – ω4 угловых скоростей тел ω1·R1 = ω2·R2 = ω3·R3 = ω4·R4. Передаточное отношение такого механизма
i1-4 = ω1/ω4 = R4/R1 = n4/n1 = d4/d1 = z4/z1,
где z1, z4 – числа зубьев соответствующих колес.
Параметры колес 2 и 3 не попали в формулу для определения передаточного отношения, поэтому их называют паразитными колёсами.
Варианты курсового задания К 2
«Определение скоростей и ускорений точек твёрдого тела при поступательном и вращательном движениях»
Для закрепления теоретического материала, изложенного в данной теме, необходимо выполнить курсовое задание К 2. По условию этого задания требуется определить скорость и ускорение точки М одного из колёс механизма в момент времени t1 (VM(t1) = ?;  (t1) = ?;
(t1) = ?; 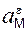 (t1) = ?
(t1) = ? 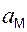 (t1) = ?).
(t1) = ?).
Схемы механизмов показаны на рисунках, а необходимые данные приведены в табл. 2.2.
Таблица 2.2
| Номер варианта | Расчётная схема механизма | Исходные данные для расчёта |

| Х = 15·t2·+ 12·t + 2, см; R2 = 60 см; r2 = 45 см; R3 = 36 см; t1 = 2 c | |
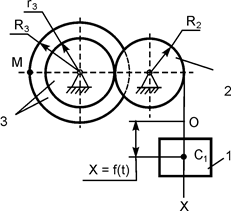
| Х = 4·t2·+ 10·t + 5, см; R2 = 80 см; R3 = 60 см; r3 = 45 см; t1 = 1 c |
Продолжение табл. 2.2
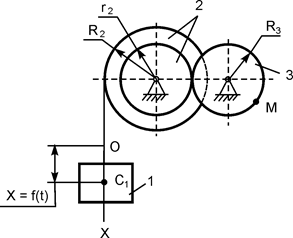
| Х = 0,5 t2 + 6·t + 8, см; R2 = 100 см; r2 = 60 см; R3 = 75 см; t1 = 2 c | |

| Х = 9,5·t2·+ 4·t + 4, см; R2 = 58 см; r2 = 45 см; R3 = 40 см; t1 = 3 c | |
| Х = 6·t2 + 15·t + 3, см; R2 = 45 см; r2 = 30 см; R3 = 80 см; t1 = 2 c |
Продолжение табл. 2.2
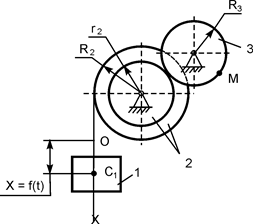
| Х = 9·t2 + 16·t + 7, см; R2 = 100 см; r2 = 45 см; R3 = 50 см; t1 = 2 c | |
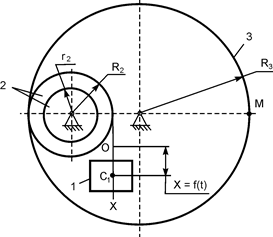
| Х = 15·t2 + 12·t + 2, см; R2 = 45 см; r2 = 35 см; R3 = 105 см; t1 = 3 c | |
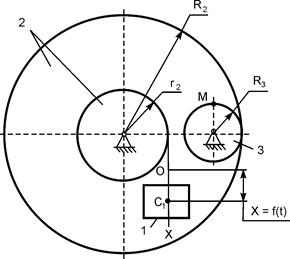
| Х = 11·t2 +10·t + 10, см; R2 = 35 см; r2 = 15 см; R3 = 10 см; t1 = 2 c |
Продолжение табл. 2.2
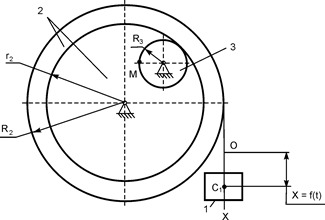
| Х = 7·t2 + 3·t + 5, см; R2 = 60 см; r2 = 45 см; R3 = 20 см; t1 = 1 c | |
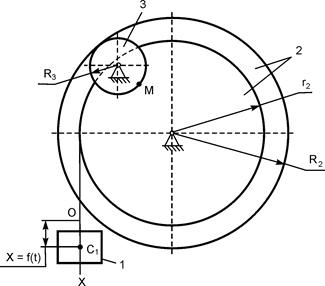
| Х = 6·t2 + 7·t + 10, см; R2 = 60 см; r2 = 45 см; R3 = 16 см; t1 = 1 c | |
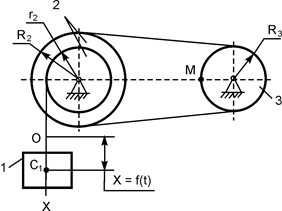
| Х = 10·t2 + 8·t + 9, см; R2 = 40 см; r2 = 25 см; R3 = 20 см; t1 = 1 c |
Продолжение табл. 2.2
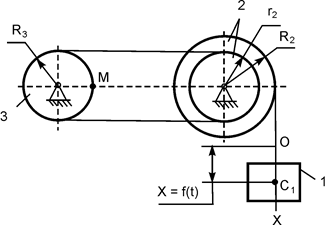
| Х = 16·t2 + 10·t + 5, см; R2 = 20 см; r2 = 15 см; R3 = 10 см; t1 = 2 c | |

| Х = 22·t2 + 7, см; R2 = 30 см; r2 = 20 см; R3 = 40 см; t1 = 2 c | |
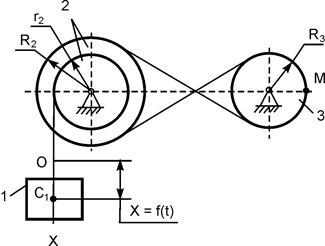
| Х = 17·t2 + 3·t + 6, см; R2 = 30 см; r2 = 20 см; R3 = 15 см; t1 = 1 c |
Продолжение табл. 2.2

| Х = 11·t2 + 2·t + 5, см; R2 = 15 см; r2 = 10 см; R3 = 15 см; t1 = 2 c | |

| Х = 12·t2 + 6·t + 4, см; R2 = 40 см; r2 = 20 см; R3 = 16 см; t1 = 3 c | |
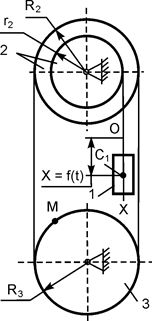
| Х = 7·t2 + 4·t + 8, см; R2 = 15 см; r2 = 10 см; R3 = 15 см; t1 = 1 c |
Продолжение табл. 2.2

| Х = 18·t2 + 10·t + 5, см; R2 = 30 см; r2 = 20 см; R3 = 30 см; t1 = 2 c | |

| Х = 18·t2 + 10·t + 5, см; R2 = 30 см; r2 = 20 см; R3 = 30 см; t1 = 2 c | |
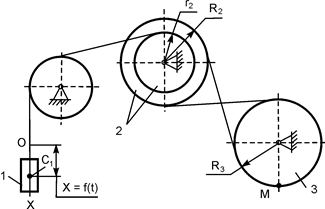
| Х = 27·t2 + 8·t + 10, см; R2 = 40 см; r2 = 20 см; R3 = 45м; t1 = 1 c |
Продолжение табл. 2.2

| Х = 13·t2 + 5·t + 6, см; R2 = 60 см; r2 = 45 см; R3 = 70 см; r3 = 40 см; t1 = 2 c | |
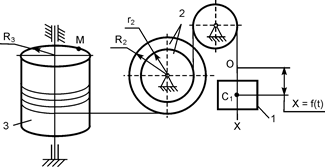
| Х = 21·t2 + 6·t + 7, см; R2 = 40 см; r2 = 20 см; R3 = 36 см; t1 = 1 c | |
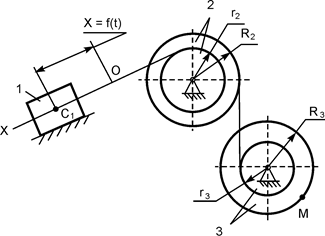
| Х = 18·t2 + 9·t + 5, см; R2 = 60 см; r2 = 45 см; R3 = 40 см; r3 = 25 см; t1 = 1 c |
Продолжение табл. 2.2
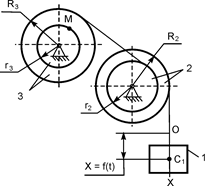
| Х = 4·t2 + 8·t + 9, см; R2 = 60 см; r2 = 45 см; R3 = 80 см; r3 = 50 см; t1 = 1 c | |
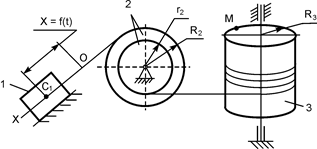
| Х = 11·t2 + 4·t + 8, см; R2 = 60 см; r2 = 45 см; R3 = 50 см; t1 = 1 c | |

| Х = 50·t2 + 14·t + 6, см; R2 = 60 см; r2 = 45 см; R3 = 60 см; r3 = 45 см; t1 = 1 c | |
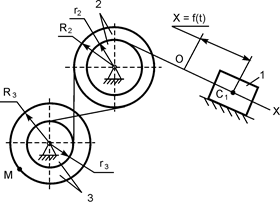
| Х = 42·t2 + 10·t + 5, см; R2 = 60 см; r2 = 45 см; R3 = 70 см; r3 = 40 см; t1 = 1 c |
Окончание табл. 2.2
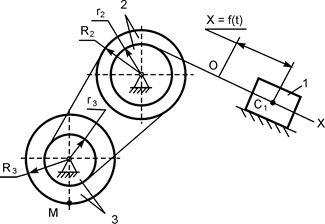
| Х = 36·t2 + 5·t + 8, см; R2 = 60 см; r2 = 45 см; R3 = 70 см; r3 = 45 см; t1 = 1 c | |
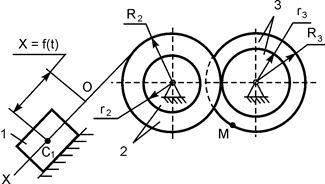
| Х = 4·t2 + 6·t + 4, см; R2 = 60 см; r2 = 45 см; R3 = 55 см; r3 = 45 см; t1 = 2 c | |

| Х = 26·t2 + 7·t + 10, см; R2 = 60 см; r2 = 45 см; R3 = 55 см; t1 = 1 c |
Пример выполнения курсового задания К 2
Дано: схема плоского механизма (рис. 2.25); уравнение движения груза 1: Х = 2·t2 + 2, см; радиусы колес: R2 = 50 см; r2 = 30 см; R3 = 60 см; r3 = 40 см. Определить кинематические характеристики точки М тела 3 в момент времени t1 = 1 c (VM(t1) = ?;  (t1) = ?;
(t1) = ?; 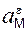 (t1) = ?
(t1) = ? 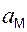 (t1) = ?).
(t1) = ?).
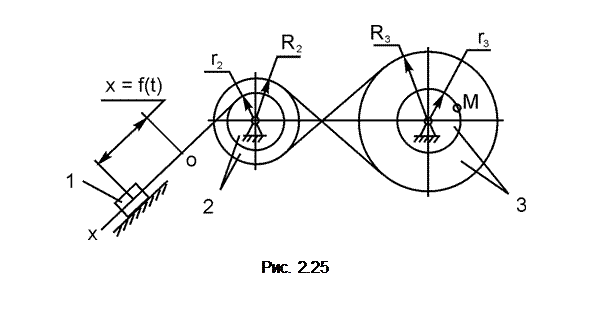
Решение. В начальный момент времени при t0 = 0 координата X(t0) = 2·(t0)2 + 2 = 2·02 + 2 = 2 см. Дифференцированием по времени уравнения движения груза 1 найдем проекцию  скорости его центра масс на ось ОХ:
скорости его центра масс на ось ОХ:
 =
= 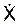 = dX/dt = d(2t2 + 2)/dt = 4·t.
= dX/dt = d(2t2 + 2)/dt = 4·t.
Так как 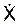 = 4·t > 0, то
= 4·t > 0, то 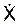 = V и, следовательно, координата Х = f(t) с течением времени увеличивается. Для графического построения определяемых кинематических характеристик изобразим механизм в произвольный момент времени t (рис. 2.26).
= V и, следовательно, координата Х = f(t) с течением времени увеличивается. Для графического построения определяемых кинематических характеристик изобразим механизм в произвольный момент времени t (рис. 2.26).
Так как груз 1 и участок АВ нити совершают поступательные движения, то справедливо равенство VB = V.
Точка В принадлежит телу 2, совершающему вращательное движение в системе отсчёта C2X2Y2Z2, поэтому модуль скорости этой точки определится из формулы VB = ω2·BC2 = ω2·r2 = I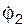 I·r2, где ω2 – модуль угловой скорости
I·r2, где ω2 – модуль угловой скорости  тела 2. Согласно рис. 2.26 вращение тела 2 происходит против хода часовой стрелки. Определим модуль ω2 угловой скорости
тела 2. Согласно рис. 2.26 вращение тела 2 происходит против хода часовой стрелки. Определим модуль ω2 угловой скорости  тела 2 по формуле ω2 = VB/r2 = V/r2. По известному модулю ω2 угловой скорости тела 2 определяется модуль VC скорости точки С тела 2:
тела 2 по формуле ω2 = VB/r2 = V/r2. По известному модулю ω2 угловой скорости тела 2 определяется модуль VC скорости точки С тела 2:
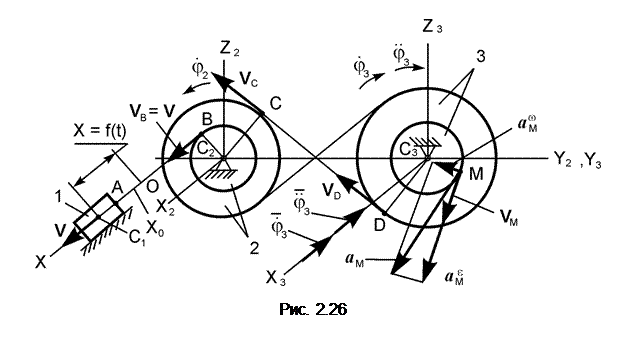
VC = ω2·CC2 = ω2·R2 = (V/r2)·R2 = V·(R2/r2).
Так как участок нити CD совершает поступательное движение, то справедливо равенство VC = VD = V·(R2/r2). С другой стороны, точка D принадлежит колесу 3. Исходя из условия принадлежности этой точки телу 3, имеем VD = ω3·R3 = V·(R2/r2), где ω3 – модуль угловой скорости  тела 3. Тело 3 осуществляет вращение в направлении хода часовой стрелки. Его угловая скорость вычисляется по формуле
тела 3. Тело 3 осуществляет вращение в направлении хода часовой стрелки. Его угловая скорость вычисляется по формуле
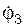 =
= 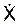 ·(R2/(r2·R3)) = (4·t)·(R2/(r2·R3)).
·(R2/(r2·R3)) = (4·t)·(R2/(r2·R3)).
По известной угловой скорости 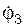 тела 3, находят его угловое ускорение
тела 3, находят его угловое ускорение 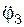 .
.
 = d
= d /dt = 4·(R2/(r2·R3)) = const > 0.
/dt = 4·(R2/(r2·R3)) = const > 0.
Так как  > 0 и
> 0 и  = const > 0, то происходит равноускоренное вращение тела 3. Определяем кинематические характеристики точки М тела 3 в момент времени (t1).
= const > 0, то происходит равноускоренное вращение тела 3. Определяем кинематические характеристики точки М тела 3 в момент времени (t1).
Модуль угловой скорости
ω3(t1) = I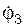 (t1)I = (4·t1)·(R2/(r2·R3)).
(t1)I = (4·t1)·(R2/(r2·R3)).
Модуль углового ускорения
ε3(t1) = 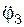 = 4·(R2/(r2·R3)).
= 4·(R2/(r2·R3)).
Модуль скорости точки М равна
VM(t1) = ω3(t1)·MC3 = ω3(t1)·r3 = (4·t1)·(R2·r3/(r2·R3)).
Модуль центростремительного ускорения точки М
 (t1) = (ω3(t1))2·MC3 = (ω3(t1))2·r3 = (4·t1·(R2/(r2·R3)))2·r3.
(t1) = (ω3(t1))2·MC3 = (ω3(t1))2·r3 = (4·t1·(R2/(r2·R3)))2·r3.
Модуль вращательного ускорения равен
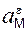 (t1) = ε3(t1)·r3 = 4·(R2·r3/(r2·R3)).
(t1) = ε3(t1)·r3 = 4·(R2·r3/(r2·R3)).
Модуль полного ускорения точки М
 .
.
Произведём вычисления для момента времени t1 = 1 c и полученные значения сведём в таблицу.
Таблица
| ω3(t1), рад/с | ε3(t1), рад/с2 | VM(t1), см/с |  (t1), см/с2 (t1), см/с2
| 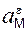 (t1), см/с2 (t1), см/с2
| 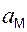 (t1), см/с2 (t1), см/с2
|
| 1,111 | 1,111 | 44,444 | 49,382 | 44,444 | 66,434 |
Кинематические характеристики точки М показаны на рис. 2.26.
2.18. Плоскопараллельное движение твёрдого тела
Плоскопараллельным (плоским) движением твёрдого тела называется такое движение, при котором каждая точка тела движется в плоскости, параллельной некоторой неподвижной плоскости.
Плоскопараллельные движения совершают многие тела механизмов и машин, например, катящееся колесо, шатун в кривошипно-ползунном механизме и др.
Рассмотрим сечение S1 тела плоскостью O1X1Y1 подвижной системы отсчёта O1X1Y1Z1, плоскости которой параллельны плоскостям неподвижной системы отсчёта OXYZ (рис. 2.27).
При плоскопараллельном движении все точки тела, лежащие на прямой А1А2, перпендикулярной сечению S1, движутся одинаково и, следовательно, траектории этих точек совпадают при наложении друг на друга, а скорости и ускорения их геометрически равны, т. е.
VA = VA1 = VA2;
aA = aA1 = aA2 .
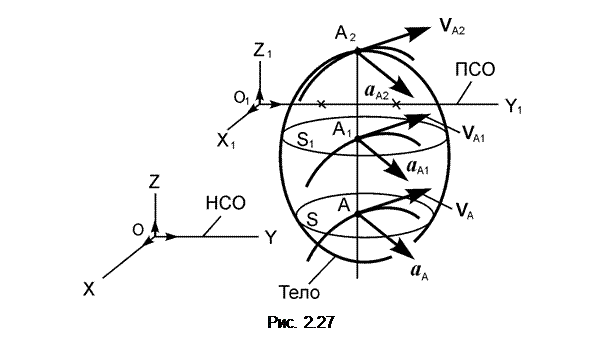
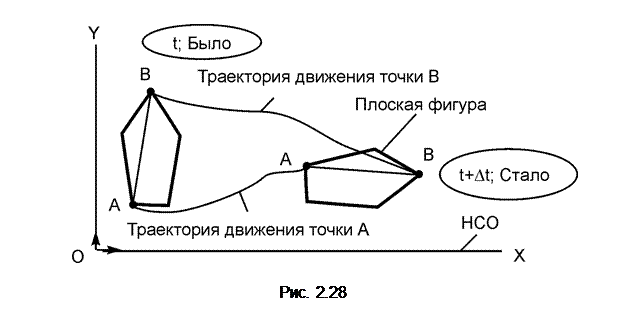
Это позволяет свести изучение плоскопараллельного движения тела к изучению движения плоской фигуры в неподвижной системе отсчёта OXY (рис. 2.28).
Так как положение плоской фигуры в системе отсчёта OXY полностью определяется положением отрезка АВ, то движение плоской фигуры можно изучать как движение прямолинейного отрезка АВ. Как видно из рис. 2.28, при плоскопараллельном движении тела траектории движения точек различны и, следовательно, скорости и ускорения точек геометрически различны.
Таким образом, плоскопараллельное движение тела заменяется рассмотрением движения прямолинейного отрезка АВ в системе отсчёта OXY.
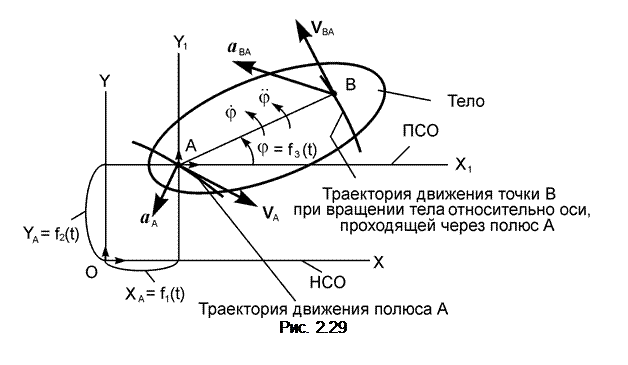
Плоскопараллельное движение тела можно представить как вращательное движение относительно подвижной оси, проходящей через полюс. На рис. 2.29 за полюс принята точка А, в которую помещено начало подвижной системы отсчёта AX1Y1, совершающей поступательное движение.
Через точку А проходит подвижная ось вращения AZ1, перпендикулярная плоскости OXY (рис. 2.29). Положение отрезка АВ в неподвижной системе отсчёта полностью определяется тремя уравнениями:
XA = f1(t); YA = f2(t); φ = f3(t).
Эти уравнения и называют уравнениями плоскопараллельного движения твёрдого тела. При этом два уравнения: XA = f1(t); YA = f2(t) описывают поступательную часть движения тела со скоростью VA и ускорением aA полюса А, а третье уравнение описывает вращательную часть движения с угловой скоростью  и угловым ускорением
и угловым ускорением  относительно подвижной оси вращения AZ1, проходящей через полюс А.
относительно подвижной оси вращения AZ1, проходящей через полюс А.
Таким образом, плоскопараллельное движение тела представляет собой сумму двух движений: поступательное движение тела со скоростью полюса А и вращательное движение с угловой скоростью  относительно оси, проходящей через полюс А. За полюс можно принять любую точку тела. Как правило, за полюс принимается центр масс тела.
относительно оси, проходящей через полюс А. За полюс можно принять любую точку тела. Как правило, за полюс принимается центр масс тела.
Зная уравнения плоскопараллельного движения тела: XA = f1(t); YA = f2(t); φ = f3(t), несложно определить скорость VA и ускорение aA полюса А, а также угловую скорость  и угловое ускорение
и угловое ускорение  по формулам:
по формулам:
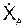 = dXA/dt;
= dXA/dt; 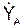 = dYA/dt;
= dYA/dt; 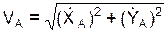 ;
;
 = d2XA/dt2;
= d2XA/dt2; 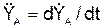 = d2YA/dt2;
= d2YA/dt2;
aA = 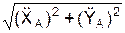 ;
;  = dφ/dt;
= dφ/dt; 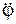 = d2φ/dt2.
= d2φ/dt2.
При вращении тела относительно оси, проходящей через полюс А (см. рис. 2.29), точка В описывает окружность радиусом, равным длине отрезка АВ. Зависимость между скоростями точек плоской фигуры устанавливается по следующей теореме.
Теорема. Скорость любой точки В плоской фигуры в неподвижной системе отсчёта OXY равна геометрической сумме скорости полюса А и скорости этой точки в её вращательном движении вместе с плоской фигурой относительно оси, проходящей через полюс:
VB = VA + VBA.
Модуль VBA вращательной скорости VBA находится по формуле
VBA = ω·BA,
где ω – модуль угловой скорости  тела.
тела.
При этом VBA ┴ ВА. Модуль скорости точки В находят по формуле
 .
.
На рис. 2.30 представлен пример определения скорости VB произвольной точки В по исходным данным, приведенным на рис. 2.29.
Определение скоростей точек тела с помощью формулы
VB = VA + VBA
связано с довольно сложными расчётами. Однако, исходя из этого основного результата, можно получить ряд других, практически более удобных и простых методов определения скоростей точек тела. Одним из этих методов является теорема: проекции скоростей точек тела на прямую, соединяющую эти точки, равны друг другу.
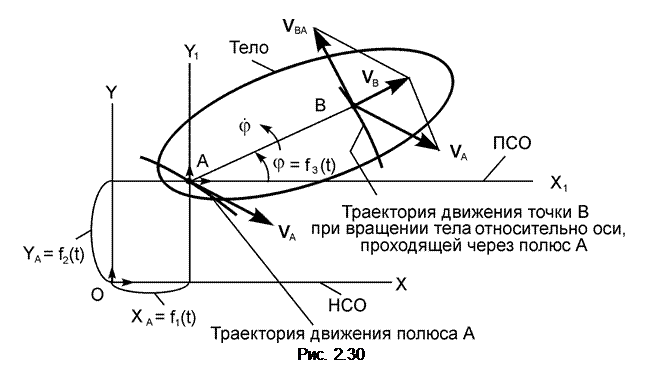
Согласно этой теореме имеем VA·cos(α) = VВ·cos(β) (рис. 2.31).
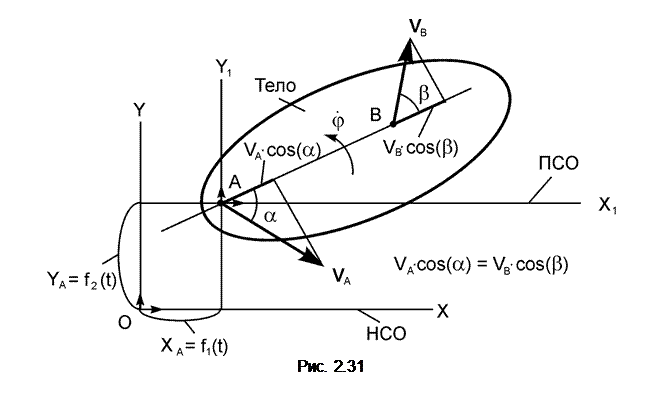
Этот результат позволяет легко находить скорость данной точки тела, если известны направление движения этой точки и скорость какой-нибудь другой точки того же тела.
Определение скоростей точек тела
С помощью мгновенного центра скоростей
Другой простой и наглядный метод определения скоростей точек при… Мгновенным центром скоростей (МЦС) называется точка сечения S тела, скорость которой в данный момент времени равна…Различные случаи определения положения
Мгновенного центра скоростей
Случай 1Варианты курсового задания К 3
«Кинематический анализ плоского механизма»
Для закрепления теоретического материала необходимо выполнить курсовое задание К 3. В курсовом задании для расчётного положения плоского механизма требуется найти модули скоростей точек А, В и С и модули угловых скоростей звеньев этого механизма.
Схемы механизмов и необходимые для расчёта данные приведены в табл. 2.3.
Таблица 2.3
| Номер варианта | Расчётная схема механизма | Исходные данные для расчёта | Определяемые величины |

|
 = 1 рад/с;
R2 = 0,4 м;
R3 = 0,6 м;
АС = 0,2 м = 1 рад/с;
R2 = 0,4 м;
R3 = 0,6 м;
АС = 0,2 м
|
VA = ?
VB = ?
VC = ?
 = ? = ?
| |
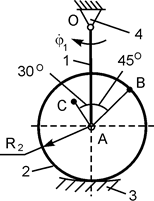
|
 = 1 рад/с;
ОА = 0,60 м;
R2 = 0,24 м;
АС = 0,12 м = 1 рад/с;
ОА = 0,60 м;
R2 = 0,24 м;
АС = 0,12 м
|
VA = ?
VB = ?
VC = ?
 = ? = ?
| |

| VA = 1 м/с; R = 0,50 м |
VB = ?
VC = ?
 = ? = ?
| |
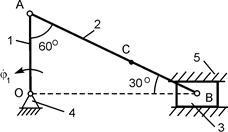
|
 = 1 рад/с;
ОА = 0,30 м;
ВС = 0,10 м = 1 рад/с;
ОА = 0,30 м;
ВС = 0,10 м
|
VA = ?
VB = ?
VC = ?
 = ? = ?
 = ? = ?
|
Продолжение табл. 2.3
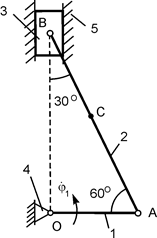
|
 = 1 рад/с;
ОА = 0,30 м;
АС = ВС = 1 рад/с;
ОА = 0,30 м;
АС = ВС
|
VA = ?
VB = ?
VC = ?
 = ? = ?
 = ? = ?
| |
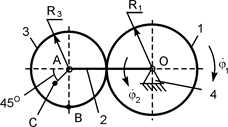
|
 = 2 рад/с; = 2 рад/с;
 = 1 рад/с;
R1 = 0,60 м;
R3 = 0,40 м;
АС = 0,20 м = 1 рад/с;
R1 = 0,60 м;
R3 = 0,40 м;
АС = 0,20 м
|
VA = ?
VB = ?
VC = ?
 = ? = ?
| |

| VA = 1 м/с;; АВ = 0,60 м; АС = 0,30 м |
VB = ?
VC = ?
 = ? = ?
 = ? = ?
 = ? = ?
| |

|
 = 1 рад/с;
ОА = 0,60 м;
АВ = 1,2 м;
АС = ВС = 1 рад/с;
ОА = 0,60 м;
АВ = 1,2 м;
АС = ВС
|
VA = ?
VB = ?
VC = ?
 = ? = ?
 = ? = ?
|
Продолжение табл. 2.3

| VA = 2 м/с; АВ = 1,00 м; АС = 0,50 м |
VB = ?
VC = ?
 = ? = ?
 = ? = ?
 = ? = ?
| |
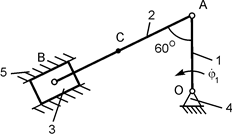
|
 = 2 рад/с;
ОА = 0,60 м;
АВ = 1,2 м;
АС = ВС = 2 рад/с;
ОА = 0,60 м;
АВ = 1,2 м;
АС = ВС
|
VA = ?
VB = ?
VC = ?
 = ? = ?
 = ? = ?
| |
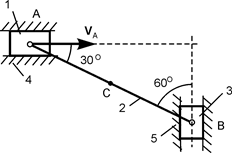
| VA = 3 м/с; АВ = 0,80 м; АС = 0,40 м |
VB = ?
VC = ?
 = ? = ?
 = ? = ?
 = ? = ?
| |
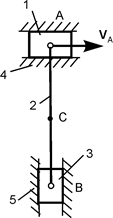
| VA = 1,5 м/с; АВ = 0,80 м; АС = 0,40 м |
VB = ?
VC = ?
 = ? = ?
 = ? = ?
 = ? = ?
|
Продолжение табл. 2.3
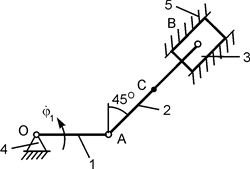
|
 = 2 рад/с;
ОА = 0,40 м;
АВ = 0,70 м;
АС = 0,35 = 2 рад/с;
ОА = 0,40 м;
АВ = 0,70 м;
АС = 0,35
|
VA = ?
VB = ?
VC = ?
 = ? = ?
 = ? = ?
| |
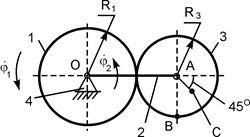
|
 = 1,5 рад/с; = 1,5 рад/с;
 = 1 рад/с;
R1 = 0,60 м;
R3 = 0,40 м;
АС = 0,20 м = 1 рад/с;
R1 = 0,60 м;
R3 = 0,40 м;
АС = 0,20 м
|
VA = ?
VB = ?
VC = ?
 = ? = ?
| |

|
 = 1 рад/с;
R2 = 0,50 м;
R3 = 0,70 м;
АС = 0,25 м = 1 рад/с;
R2 = 0,50 м;
R3 = 0,70 м;
АС = 0,25 м
|
VA = ?
VB = ?
VC = ?
 = ? = ?
| |

|
 = 1,5 рад/с;
ОА = 0,60 м;
R2 = 0,25 м = 1,5 рад/с;
ОА = 0,60 м;
R2 = 0,25 м
|
VA = ?
VB = ?
VC = ?
 = ? = ?
|
Продолжение табл. 2.3
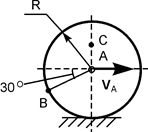
| VA = 3 м/с; R = 0,60 м; АС = 0,30 м |
VB = ?
VC = ?
 = ? = ?
| |
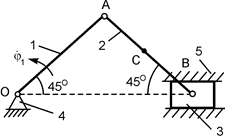
|
 = 1,5 рад/с;
ОА = 1,00 м;
АС = 0,5 м = 1,5 рад/с;
ОА = 1,00 м;
АС = 0,5 м
|
VA = ?
VB = ?
VC = ?
 = ? = ?
 = ? = ?
| |
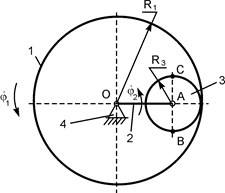
|
 = 1 рад/с; = 1 рад/с;
 = 3 рад/с;
R1 = 0,60 м;
R3 = 0,20 м = 3 рад/с;
R1 = 0,60 м;
R3 = 0,20 м
|
VA = ?
VB = ?
VC = ?
 = ? = ?
| |
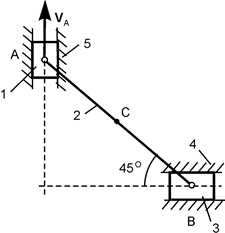
| VA = 2 м/с; АВ = 0,80 м; АС = 0,40 м |
VB = ?
VC = ?
 = ? = ?
 = ? = ?
 = ? = ?
|
Продолжение табл. 2.3

|
 = 1 рад/с;
ОА = 0,60 м;
АВ = 0,90 м;
АС = 0,45 м = 1 рад/с;
ОА = 0,60 м;
АВ = 0,90 м;
АС = 0,45 м
|
VA = ?
VB = ?
VC = ?
 = ? = ?
 = ? = ?
| |
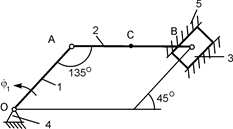
|
 = 2 рад/с;
ОА = 0,50 м;
АВ = 0,50 м;
АС = 0,25 м = 2 рад/с;
ОА = 0,50 м;
АВ = 0,50 м;
АС = 0,25 м
|
VA = ?
VB = ?
VC = ?
 = ? = ?
 = ? = ?
| |
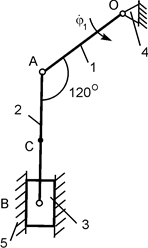
|
 = 2 рад/с;
ОА = 0,60 м;
АВ = 0,70 м;
АС = 0,35 м = 2 рад/с;
ОА = 0,60 м;
АВ = 0,70 м;
АС = 0,35 м
|
VA = ?
VB = ?
VC = ?
 = ? = ?
 = ? = ?
| |
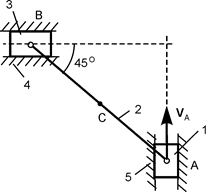
| VA = 2 м/с; АВ = 1,00 м; АС = 0,50 м |
VB = ?
VC = ?
ω1 = ?
 = ? = ?
 = ? = ?
|
Продолжение табл. 2.3

|
 = 1,5 рад/с;
ОА = 0,40 м;
АВ = 0,90 м;
АС = 0,30 м = 1,5 рад/с;
ОА = 0,40 м;
АВ = 0,90 м;
АС = 0,30 м
|
VA = ?
VB = ?
VC = ?
 = ? = ?
 = ? = ?
| |
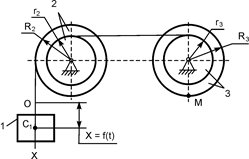
|
 = 1 рад/с; = 1 рад/с;
 = 2,5 рад/с;
R1 = 0,60 м;
R3 = 0,20 м = 2,5 рад/с;
R1 = 0,60 м;
R3 = 0,20 м
|
VA = ?
VB = ?
VC = ?
 = ? = ?
| |

|
 = 1 рад/с;
ОА = 0,70 м;
R2 = 0,30 м = 1 рад/с;
ОА = 0,70 м;
R2 = 0,30 м
|
VA = ?
VB = ?
VC = ?
 = ? = ?
| |
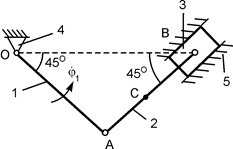
|
 = 1,6 рад/с;
ОА = 0,40 м;
АВ = 0,70 м;
АС = 0,35 м = 1,6 рад/с;
ОА = 0,40 м;
АВ = 0,70 м;
АС = 0,35 м
|
VA = ?
VB = ?
VC = ?
 = ? = ?
 = ? = ?
|
Окончание табл. 2.3

|
 = 2,8 рад/с;
ОА = 0,30 м;
АВ = 0,60 м;
АС = 0,30 м = 2,8 рад/с;
ОА = 0,30 м;
АВ = 0,60 м;
АС = 0,30 м
|
VA = ?
VB = ?
VC = ?
 = ? = ?
 = ? = ?
| |

|
 = 2,2 рад/с;
ОА = 0,50 м;
АС = 0,30 м = 2,2 рад/с;
ОА = 0,50 м;
АС = 0,30 м
|
VA = ?
VB = ?
VC = ?
 = ? = ?
 = ? = ?
|
Пример выполнения курсового задания К 3
Дано: схема плоского механизма (рис. 2.39); модуль угловой скорости ведущего звена 1; ω1 = ωАО1 = 1 рад/с; геометрические параметры: АВ = О2В = 1 м; АС = СВ = 0,5 м. Определить модули скоростей точек А, В, С и модули ω2, ω3 угловых скоростей звеньев АВ и ВО2 механизма.
Решение. Согласно расчётной схеме рассматриваемый механизм состоит из трёх звеньев, обозначенных на рис. 2.39 позициями 1, 2, 3. Звено 1 (АО1) ведущее, остальные ведомые. Звенья совершают следующие виды движений: 1 – вращательное, 2 – плоскопараллельное, 3 – вращательное.
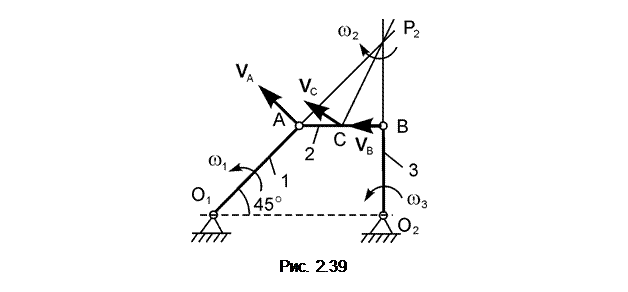
Из условия принадлежности точки А звену 1, совершающему вращательное движение, определим модуль скорости VA.
VA = ωOA·AO1 =
= ω1·AO1 = ω1·(BO2/sin(45о)) = 1·(1/0,707) = 1,414 м/с.
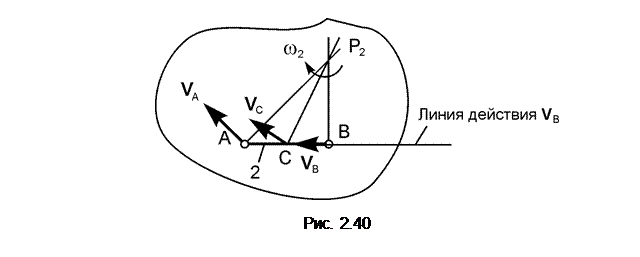
Рассмотрим отдельно плоскопараллельное движение тела 2 (рис. 2.40).
Вектор скорости VA покажем на рис. 2.40. VA ┴ AO1.
Как известно, условием безаварийной работы механизма является общая скорость в месте контакта звеньев. Исходя из этого, у звена 2 скорость точки А известна. Точка В, из условия её принадлежности звену 3, описывает окружность, поэтому линия действия скорости VB перпендикулярна ВО2 (VB ┴ BO2).
Таким образом, у звена 2 известен вектор VA скорости точки А и линия действия вектора VB. Так как звено 2 совершает плоскопараллельное движение, то для определения мгновенного центра скоростей (точка Р2) используется первый случай (см. рис. 2.33). МЦС находится на пересечении перпендикуляров к скоростям точек А и В. По направлению скорости VA точки А определим направление вращения звена 2 относительно оси, проходящей через точку Р2. Из условия принадлежности точки А звену 2, совершающему плоскопараллельное движение, справедливо равенство VA = ω2·AP2 где ω2 – модуль угловой скорости тела 2. Так как AP2 = AO1 = BO2/sin(45о), то VA = ω2·(BO2/sin(45о)). Из последнего равенства определим модуль ω2 угловой скорости звена 2.
ω2 = VA·sin(45о)/BO2 = (1,414·0,707)/1 = 1,000 рад/с.
По известному модулю угловой скорости тела 2 определим модули скоростей точек В и С:
VB = ω2·BP2 = 1·1 = 1, 000 м/с;
VC = ω2·CP2 = ω2·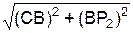 = 1·
= 1·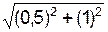 = 1, 118 м/с.
= 1, 118 м/с.
Из условия принадлежности точки В телу 3, совершающему вращательное движение, справедливо равенство VB = ω3·BO2, где ω3 – модуль угловой скорости тела 3. Из этого равенства модуль угловой скорости вращательного движения звена 3 равен
ω3 = VB/BO2 = 1/1 = 1,000 рад/с.
Полученные результаты расчёта вносятся в таблицу.
Таблица
| VA, см/с | VB, см/с | VC, см/с | ω2, рад/с | ω3, рад/с |
| 1,414 | 1,000 | 1,118 | 1,000 | 1,000 |
Скорости точек А, В, С показаны на рис. 2.39.
Вопросы и задания для самоконтроля
1. Сформулировать определение термина «поступательное движение твёрдого тела».
2. Записать уравнения поступательного движения тела в пространстве в декартовой системе отсчёта.
3. Записать уравнения поступательного движения тела на плоскости OXY.
4. Записать уравнения прямолинейного поступательного движения тела по горизонтали.
5. Записать выражения для определения проекций скорости центра масс на координатные оси декартовой системы отсчёта.
6. Записать выражение для определения модуля скорости центра масс тела при его поступательном движении в декартовой системе отсчёта.
7. Записать выражения для определения проекций ускорения центра масс на координатные оси декартовой системы отсчёта.
8. Записать выражение для определения модуля ускорения центра масс тела при его поступательном движении в декартовой системе отсчёта.
9. Сформулировать определение термина «вращательное движение твёрдого тела».
10. Записать уравнение вращательного движения тела.
11. Сформулировать определение термина «угловая скорость».
12. Записать формулу для определения угловой скорости вращательного движения тела.
13. Сформулировать определение термина «угловое ускорение».
14. Записать формулу для определения углового ускорения тела.
15. Записать формулу для определения модуля скорости точки при вращательном движении тела.
16. Записать формулу для определения вектора ускорения точки при вращательном движении тела.
17. Записать формулу для определения модуля центростремительного ускорения точки.
18. Записать формулу для определения модуля вращательного ускорения точки.
19. Записать формулу для определения модуля ускорения точки тела при его вращательном движении.
20. Записать уравнение равномерного вращательного движения тела.
21. Записать уравнение равнопеременного вращательного движения тела.
22. При каком сочетании угловой скорости и углового ускорения происходит ускоренное вращение тела?
24. При каком сочетании угловой скорости и углового ускорения происходит замедленное вращение тела?
25. Где прикладывают и как направляют вектор угловой скорости тела?
26. Где прикладывают и как направляют вектор углового ускорения тела при его ускоренном вращении?
27. Сформулировать определение термина «плоскопараллельное движение твёрдого тела».
28. Записать уравнения плоскопараллельного движения тела.
29. Записать формулу для определения вектора скорости точки при плоскопараллельном движении тела.
30. Сформулировать определение термина «мгновенный центр скоростей».
Сложное движение точки
В ряде случаев при решении задач механики оказывается целесообразным (а иногда… Введем следующие понятия, применяемые в сложном движении точки.Сложение скоростей
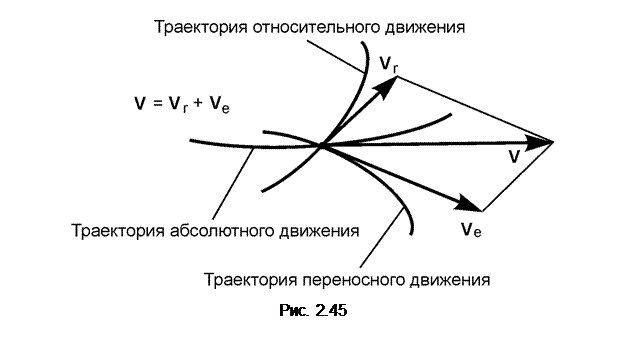
Рассматривается сложное движение точки на плоскости (рис. 2.45).
Поскольку абсолютное движение представляет собой сумму относительного и переносного движений, то справедлива следующая теорема: при сложном движении абсолютная скорость V точки равна геометрической сумме относительной Vr и переносной Ve скоростей:
V = Vr + Ve.
Построенная на рис. 2.45 фигура называется параллелограммом скоростей. Модуль абсолютной скорости находится по формуле
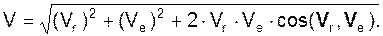
Сложение ускорений (теорема Кориолиса)
Теорема. При сложном движении точки её абсолютное ускорение равно геометрической сумме относительного, переносного и кориолисова ускорений:
a = ar + ae + ac ,
где ar – относительное ускорение; ae – переносное ускорение; ac – ускорение Кориолиса.
Доказательство теоремы Кориолиса достаточно сложно и здесь не приводится.
Кориолисовым ускорением называется составляющая абсолютного ускорения точки в сложном движении, равная удвоенному векторному произведению угловой скорости переносного вращения на относительную скорость точки:
ac = 2( xVr),
xVr),
где  – вектор угловой скорости переносного вращения.
– вектор угловой скорости переносного вращения.
Согласно правилу векторного произведения ac ┴  , ac ┴ Vr.
, ac ┴ Vr.
Кориолисово ускорение характеризует:
1) изменение модуля и направления переносной скорости точки вследствие её относительного движения;
Изменение направления относительной скорости точки вследствие вращательного переносного движения.
Пусть в момент времени t человек занимает на платформе положение, показанное… Так как относительное движение равномерное и прямолинейное, то относительное ускорение человека ar = 0. Однако за…Варианты курсового задания К 4
«Определение абсолютной скорости
и абсолютного ускорения точки»
По заданным уравнениям относительного движения точки М и движения тела D определить для момента времени t1 абсолютные скорость и ускорение точки М. Схемы механизмов показаны на рисунках, а необходимые для расчёта данные приведены в табл. 2.4.
Определить кинематические характеристики точки М в момент времени t1 (OM(t1) – положение точки на траектории относительного движения; Ve(t1) – переносная скорость; Vr(t1) – относительная скорость; V(t1) – абсолютная скорость; ar(t1) – относительное ускорение; aе(t1) – переносное ускорение; aс(t1) – ускорение Кориолиса; a(t1) – абсолютное ускорение).
Для каждого варианта положение точки М на расчётной схеме соответствует положительному значению дуговой координаты ОМ = f(t).
Таблица 2.4
| Номер варианта | Расчётная схема механизма | Исходные данные для расчёта |
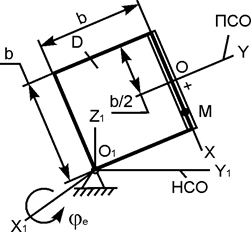
| ОМ = 18·sin(p·t/4), см; φe = 2·t3 – t2, рад; b = 25 см; t1 = 2/3 c |
Продолжение табл. 2.4
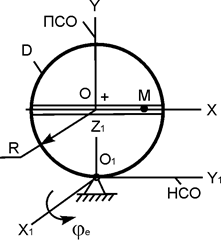
| ОМ = 20·sin(p·t), см; φe = 0,4·t2 + t, рад; R = 20 см; t1 = 5/3 c | |
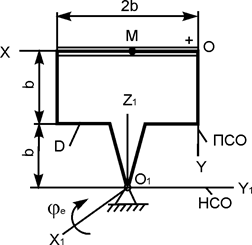
| ОМ = 6·t3, см; φe = 2·t + 0,5·t2, рад; b = 30 см; t1 = 2 c | |

| ОМ = 10·sin(p·t/6), см; φe = 0,6·t2, рад; α = 30o; t1 = 1 c |
Продолжение табл. 2.4

| ОМ = 40·p·сos(p·t/6), см; φe = 3·t – 0,5·t3, рад; R = 30 см; t1 = 2 c | |

| ОМ = 6·t2, см; φe = 2·t + 4·t2, рад; b = 30 см; t1 = 1 c | |
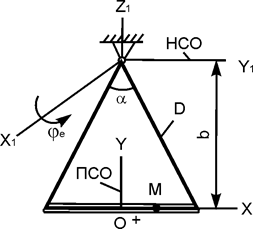
| ОМ = 20·p·сos(2·p·t), см; φe = 0,5·t2, рад; b = 40 см; α = 60o; t1 = 3/8 c |
Продолжение табл. 2.4
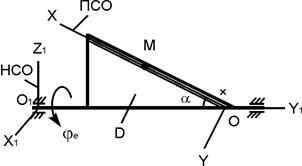
| ОМ = 6·(t + 0,5·t2), см; φe = t3 – 5·t, рад; b = 40 см; α = 30o; t1 = 2 c | |
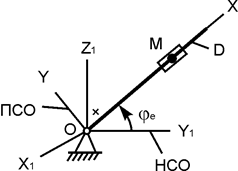
| ОМ = 10·(1+sin(2·p·t)), см; φe = 4t + 1,6t2, рад; t1 = 1/8 c | |

| ОМ = 20·p·сos(p·t/4), см; φe = 1,2·t – t2, рад; R = 20 см; b = 20 см; t1 = 4/3 c | |
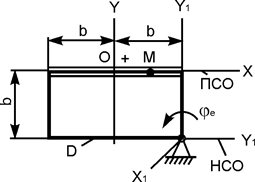
| ОМ = 20·sin(p·t/3), см; φe = 2·t2 – 0,5·t, рад; b = 25 см; t1 = 4 c |
Продолжение табл. 2.4
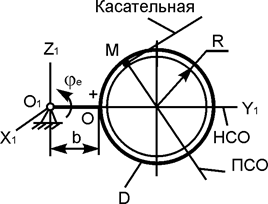
| ОМ = 15·p·t3/8, см; φe = 5·t – 4·t2, рад; R = 30 см; b = 30 см; t1 = 2 c | |
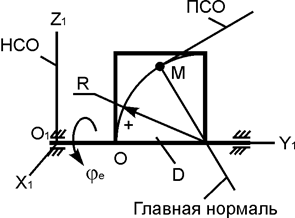
| ОМ = 120·p·t2, см; φe = 8·t2 – 3·t, рад; R = 40 см; t1 = 1/3 c | |
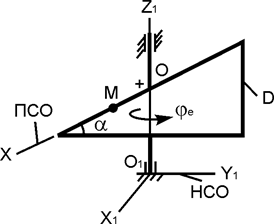
| ОМ =3+14·sin(p·t), см; φe = 4·t – 2·t2, рад; α = 30o; t1 = 2/3 c |
Продолжение табл. 2.4

|
ОМ = 5·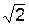 ·(t2 + t), см;
φe = 0,2·t3 + t; рад;
t1 = 2 c;
b = 60 см;
α = 45o ·(t2 + t), см;
φe = 0,2·t3 + t; рад;
t1 = 2 c;
b = 60 см;
α = 45o
| |
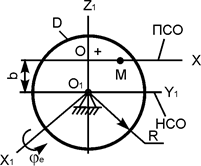
| ОМ = 20·sin(p·t), см; φe = t – 0,5·t2, рад; b = 20 см; t1 = 1/3 c | |
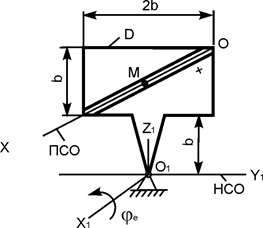
|
ОМ = 8·t3 + 2·t, см;
φe = 0,5·t2, рад;
b = 4·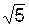 см;
t1 = 1 c см;
t1 = 1 c
| |
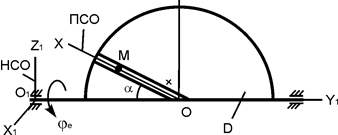
| ОМ = 10t + t3, см; φe = 8t – t2, рад; α= 30o; t1 = 2 c |
Продолжение табл. 2.4

| ОМ = 6·t + 4·t3, см; φe = t + 3·t2, рад; R = 40 см; t1 = 2 c | |

| ОМ = 30·p·cos(p·t/8), см; φe = 6·t + t2, рад; R = 60 см; t1 = 2 c | |

| ОМ = 25·(t + t2), см; φe = 2·t – 4·t2, рад; R = 25 см; t1 = 1/2 c | |
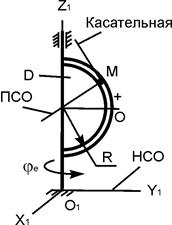
| ОМ = 10·p·sin(p·t/4), см; φe = 4·t – 0,2·t2, рад; R = 30 см; t1 = 2/3 c |
Продолжение табл. 2.4
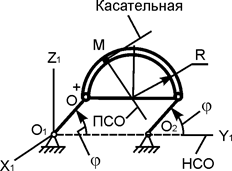
| ОМ = 6·p·t2, см; φ = p·t3/6, рад; R = 18 см; OO1 =20 см; t1 = 1 c | |
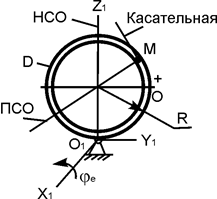
| ОМ = 75·p (0,1·t2), см; φe = 2·t – 0,3·t2, рад; R = 30 см; t1 = 1 c | |

| ОМ = 15·sin(p·t/3), см; φe = 10·t – 0,1·t2, рад; t1 = 5 c | |
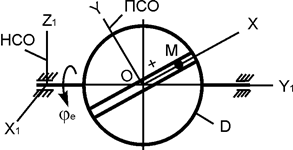
| ОМ = 8·cos(p·t/3), см; φe = 2·p·t2, рад; α = 45o; t1 = 3/2 c |
Окончание табл. 2.4
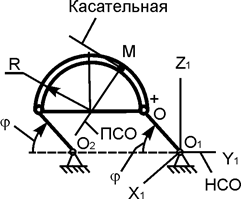
| ОМ = 6·p·t2, см; φ = p·t2/6, рад; R = 20 см; OO1 =20 см; t1 = 1 c | |
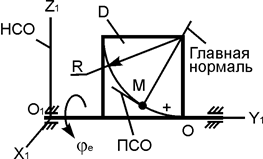
| ОМ = 2,5·p·t2, см; φe = 2·t3 – 5·t, рад; R = 40 см; t1 = 2 c | |
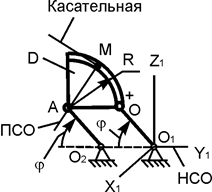
| ОМ = 6·p·t, см; φ = p·t/6, рад; R = 20 см; OO1 =20 см; t1 = 1 c | |
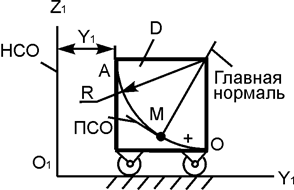
| ОМ = 4·p·t2, см; Y1= t3 + 4·t; R = 48 см; t1 = 2 c |
Пример выполнения курсового задания К 4
Дано: уравнение относительного движения точки М
OM = Sr = Sr(t) = 2,5·p·t2, см;
уравнение вращательного движения тела D
φe = φe(t) = 2·t3 – 5·t, рад;
t1 = 1 c; R = 40 см.

Точка М движется по телу D. По заданным уравнениям относительного движения точки М и движения тела D определить для заданного момента времени t1 абсолютную скорость и абсолютное ускорение точки М (OM(t1) = ? Vr(t1) = ? Ve(t1) = ? V(t1) = ? ar(t1) = ? ae(t1) = ? ac(t1) = ? a(t1) = ?) (рис. 2.49).
Решение. Точка М осуществляет сложное движение, поэтому для решения задачи необходимо ввести неподвижную систему отсчёта O1X1Y1Z1 и подвижную систему отсчёта OXYZ. Изобразим рассматриваемый механизм в момент времени t1 (рис. 2.50).
Координатную ось O1Y1 неподвижной системы отсчёта направим по оси вращения тела D. Подвижную систему отсчёта OXYZ закрепим на теле D, расположив начало отсчёта в точке О. По исходным данным уравнение относительного движения точки М задано естественным способом Sr(t) = 2,5·p·t2. Исходя из этого, известны следующие характеристики движения: вид траектории движения – дуга окружности радиусом R; начало отсчёта дуговой координаты Sr – точка О; положительное направление отсчёта дуговой координаты Sr – знак (+); уравнение движения Sr = 2,5·p·t2.

Определим положение точки М на траектории относительного движения в момент времени t1:
Sr(t1) = 2·p·(t1)2 = 2,5·p·22 = 10p см > 0.
Для координации точки М на траектории относительного движения целесообразно использовать центральный угол:
a(t1) = Sr(t1)/R = 2,5·p·(t1)2/R = 2,5·p·22/40 = p/4.
Итак, α(t1) = 45о. Точка М тела D, совершающего вращательное движение в неподвижной системе отсчёта O1X1Y1Z1, описывает окружность радиусом
MK = R – R·cos(α(t1)) = R·(1 – cos(α(t1))= 40·(1 – 0,707) = 11,72 см.
Таким образом, траектория переносного движения точки М установлена. Это окружность радиусом МК с центром в точке К, расположенной на оси вращения тела D.
Абсолютное движение точки М – это сумма относительного и переносного движений. Таким образом, траектория абсолютного движения точки М представляет собой винтовую линию, расположенную на сферическом конусе.
Для определения абсолютной скорости V точки М используется векторное равенство
V = Vr + Ve,
где Vr – вектор относительной скорости; Ve – вектор переносной скорости.
Определим проекцию  относительной скорости Vr на касательную:
относительной скорости Vr на касательную:
 =
=  = 5·p·t.
= 5·p·t.
В момент времени t1 имеем
 (t1) =
(t1) =  (t1) = 5·p·t1 = 5·p·2 = 10·p = 31,4 см/c > 0.
(t1) = 5·p·t1 = 5·p·2 = 10·p = 31,4 см/c > 0.
Поскольку  (t1) > 0, то модуль относительной Vr(t1) =
(t1) > 0, то модуль относительной Vr(t1) = 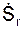 (t1), а вектор относительной скорости Vr направлен так же, как и единичный вектор τ естественной координатной системы отсчёта. Покажем этот вектор на рис. 2.50.
(t1), а вектор относительной скорости Vr направлен так же, как и единичный вектор τ естественной координатной системы отсчёта. Покажем этот вектор на рис. 2.50.
Для определения переносной скорости Ve предварительно найдем модуль ωе угловой скорости 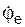 переносного вращения.
переносного вращения.
ωe = I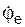 I = I6·t2 – 5I.
I = I6·t2 – 5I.
В момент времени (t1) имеем
ωe(t1) = I6·(t1)2 – 5I = I6·22 – 5I = 19 рад/c > 0.
Поскольку ωe(t1) > 0, то величина угла φе возрастает. Покажем на рис. 2.50 направление вращения и определим модуль переносной скорости Ve(t1) по формуле
Ve(t1) = ωe(t1)·МК = 19·11,72 = 222,68 см/с.
Так как Ve(t1) направлена по касательной к траектории переносного движения, то она перпендикулярна плоскости OYZ подвижной системы отсчёта. С другой стороны, Vr ┴ Ve. Исходя из этого, определим модуль абсолютной скорости:
V(t1) = 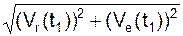 =
= 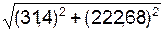 = 224,88 см/с.
= 224,88 см/с.
Если Vr не перпендикулярна Ve, то определение модуля скорости V следует определять через проекции векторного выражения V = Vr + Ve на координатные оси неподвижной системы отсчёта O1X1Y1Z1.
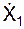 = Ve;
= Ve; 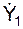 = – Vr·cos(α);
= – Vr·cos(α); 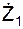 = Vr·sin(α),
= Vr·sin(α),
где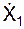 ,
, 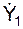 ,
, 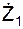 – проекции абсолютной скорости на оси O1X1, O1Y1, O1Z1 системы отсчёта O1X1Y1Z1.
– проекции абсолютной скорости на оси O1X1, O1Y1, O1Z1 системы отсчёта O1X1Y1Z1.
V(t1) = 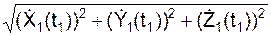 =
=
= =
=
=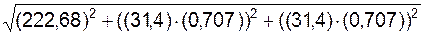 = 224,88 см/с.
= 224,88 см/с.
Для ориентации абсолютной скорости Vв пространстве неподвижной системы отсчёта определим направляющие косинусы.
cos(V,i1) = 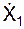 (t1)/V(t1) = 222,68/224,88 = 0,990;
(t1)/V(t1) = 222,68/224,88 = 0,990;
cos(V,j1) = 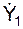 (t1)/V(t1) = (– 31,4·0,707)/224,88 = – 0,098;
(t1)/V(t1) = (– 31,4·0,707)/224,88 = – 0,098;
cos(V,k1) = 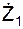 (t1)/V(t1) = (31,4·0,707)/224,88 = 0,098.
(t1)/V(t1) = (31,4·0,707)/224,88 = 0,098.
При определении абсолютного ускорения a точки М используется формула
a = ar + ae + ac ,
где ar – относительное ускорение; ae – переносное ускорение; ac – ускорение Кориолиса.
Поскольку относительное движение задано естественным способом, то справедливо равенство
ar = 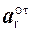 +
+ 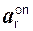 ,
,
где 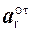 – относительное касательное ускорение;
– относительное касательное ускорение; 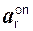 – относительное нормальное ускорение.
– относительное нормальное ускорение.
Так как переносное движение является вращательным, то переносное ускорение ae находят по формуле
ae = 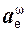 +
+ 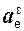 ,
,
где 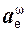 – переносное центростремительное ускорение;
– переносное центростремительное ускорение; 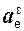 – переносное вращательное ускорение.
– переносное вращательное ускорение.
Исходную формулу для определения абсолютного ускорения можно представить в следующем виде:
a = 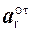 +
+ 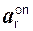 +
+ 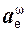 +
+ 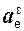 + ac .
+ ac .
Приступаем к определению слагаемых в правой части последнего выражения.
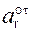 =
=  = d
= d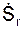 /dt = d(5·p·t)/dt = 5·p = const.
/dt = d(5·p·t)/dt = 5·p = const.
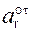 (t1) = 5·p = 5·3,14 = 15,7 см/с2 > 0 = const.
(t1) = 5·p = 5·3,14 = 15,7 см/с2 > 0 = const.
Так как 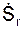 и
и  имеют одинаковые знаки, то в относительном движении точка М движется равноускоренно. Покажем вектор
имеют одинаковые знаки, то в относительном движении точка М движется равноускоренно. Покажем вектор 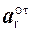 (t1) на рис. 2.50.
(t1) на рис. 2.50.
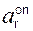 (t1) = (Vr(t1))2/ρ = (Vr(t1))2/R = (3,14)2/40 = 24,64 см/с2 .
(t1) = (Vr(t1))2/ρ = (Vr(t1))2/R = (3,14)2/40 = 24,64 см/с2 .
Вектор 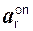 (t1) направлен по главной нормали к центру кривизны траектории относительного движения.
(t1) направлен по главной нормали к центру кривизны траектории относительного движения.
Модуль ar(t1) относительного ускорения ar(t1) в момент времени t1 определим по формуле
ar(t1) =  =
=
=  = 29,276 cм/c2.
= 29,276 cм/c2.
Модуль 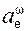 (t1) переносного центростремительного ускорения
(t1) переносного центростремительного ускорения 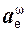 (t1) в момент времени t1 определим по формуле
(t1) в момент времени t1 определим по формуле
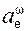 (t1) = (ωe(t1))2·MK = (19)2·11,72 = 4230,92 см/с2.
(t1) = (ωe(t1))2·MK = (19)2·11,72 = 4230,92 см/с2.
Вектор 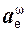 (t1) направлен к оси переносного вращения. Покажем его на рис. 2.50.
(t1) направлен к оси переносного вращения. Покажем его на рис. 2.50.
Для определения переносного вращательного ускорения 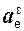 необходимо предварительно определить модуль εе переносного углового ускорения
необходимо предварительно определить модуль εе переносного углового ускорения  .
.
εe = I I = Id
I = Id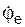 /dtI = Id(6·t2 – 5)/dtI = I12·tI.
/dtI = Id(6·t2 – 5)/dtI = I12·tI.
εe(t1) = 12·t1 = 12·2 = 24 рад/с2.
Так как 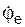 и
и  имеют одинаковые знаки, то переносное вращение происходит ускоренно. Исходя из этого, направления
имеют одинаковые знаки, то переносное вращение происходит ускоренно. Исходя из этого, направления 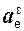 и Ve совпадают.
и Ve совпадают.
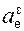 (t1) = εe(t1)·МК = 24·11,72 = 281,28 см/с2.
(t1) = εe(t1)·МК = 24·11,72 = 281,28 см/с2.
Покажем вектор 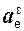 (t1) на рис. 2.50.
(t1) на рис. 2.50.
Модуль ae(t1) переносного ускорения aе(t1) в момент времени t1 определим по формуле
aе(t1) = 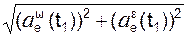 =
=
=  = 4240,259 cм/c2.
= 4240,259 cм/c2.
Приступаем к определению модуля ускорения Кориолиса.
ac(t1) = 2ωе(t1)·Vr(t1)·sin( (t1), Vr(t1)).
(t1), Vr(t1)).
Согласно определению вектор  переносной угловой скорости лежит на оси вращения тела D и направлен в сторону увеличения координаты Y1 (см. рис 2.50).
переносной угловой скорости лежит на оси вращения тела D и направлен в сторону увеличения координаты Y1 (см. рис 2.50).
ac(t1) = 2ωе(t1)·Vr(t1)·sin( (t1), Vr(t1)) = 2ωе(t1)·Vr(t1)·sin(135o) =
(t1), Vr(t1)) = 2ωе(t1)·Vr(t1)·sin(135o) =
= 2·19·31,4·0,707 = 843,59 см/с2.
По правилу векторного произведения (ac = 2( xVr)) ускорение Кориолиса ac направлено так же, как и векторы Ve и
xVr)) ускорение Кориолиса ac направлено так же, как и векторы Ve и 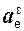 . Покажем вектор ускорения Кориолиса на рис. 2.50.
. Покажем вектор ускорения Кориолиса на рис. 2.50.
Таким образом, в векторном равенстве
a = 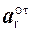 +
+ 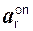 +
+ 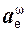 +
+ 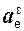 + ac
+ ac
известны все слагаемые, находящиеся в его правой части.
Определим модуль a(t1) абсолютного ускорения a(t1) через его проекции 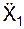 (t1),
(t1), 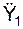 (t1),
(t1), 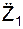 (t1) на оси неподвижной системы отсчёта O1X1Y1Z1 в момент времени (t1).
(t1) на оси неподвижной системы отсчёта O1X1Y1Z1 в момент времени (t1).
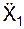 (t1) =
(t1) = 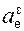 (t1) + ac(t1) = 281,28 + 843,59 = 1124,87 см/с2;
(t1) + ac(t1) = 281,28 + 843,59 = 1124,87 см/с2;
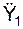 (t1) = –
(t1) = – 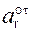 (t1)·cos(α(t1)) +
(t1)·cos(α(t1)) + 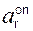 (t1)·sin(α(t1)) =
(t1)·sin(α(t1)) =
= – 15,7·0,707 + 24,64·0,707 = 6,32 см/с2;
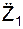 (t1) =
(t1) = 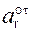 (t1)·sin(α(t1)) +
(t1)·sin(α(t1)) + 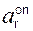 (t1)·cos(α(t1)) –
(t1)·cos(α(t1)) – 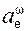 (t1) =
(t1) =
= 15,7·0,707 + 24,64·0,707 – 4230,92 = – 4202,39 см/с2;
a(t1) =  = 4350,01 см/с2.
= 4350,01 см/с2.
Для ориентации абсолютного ускорения в пространстве определим направляющие косинусы.
cos(a, i1) = 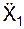 (t1)/a(t1) = 1124,87/4350,01 = 0,258;
(t1)/a(t1) = 1124,87/4350,01 = 0,258;
cos(a, j1) = 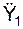 (t1)/a(t1) = 6,32/4350,01 = 0,001;
(t1)/a(t1) = 6,32/4350,01 = 0,001;
cos(a, k1) = 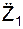 (t1)/a(t1) = – 4202,39/4350,01 = – 0,966.
(t1)/a(t1) = – 4202,39/4350,01 = – 0,966.
Результаты расчётов сводятся в таблицу.
Таблица
Кинематические характеристики точки М в момент времени t1
| Sr(t1), см | Vr(t1), см/с | Ve(t1), см/с | V(t1), см/с |  (t1),
см/с2 (t1),
см/с2
| 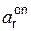 (t1),
см/с2 (t1),
см/с2
| 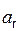 (t1),
см/с2 (t1),
см/с2
|
| 31,400 | 31,400 | 222,688 | 224,880 | 15,700 | 24,640 | 29,276 |
Окончание таблицы
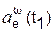 , см/с2 , см/с2
|  , см/с2 , см/с2
| 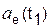 , см/с2 , см/с2
| ωe(t1), рад/с | εe(t1), рад/с2 | ac(t1), см/с2 | a(t1), см/с2 |
| 4230,920 | 281,280 | 4240,259 | 19,000 | 24,000 | 843,590 | 4350,010 |
2.28. Сферическое движение твёрдого тела
Рассмотрим движение тела, одна из точек которого во всё время движения остается неподвижной. При таком движении все остальные точки тела движутся по сферическим поверхностям, центры которых совпадают с неподвижной точкой. Такое движение называют сферическим движением твёрдого тела.
Сферическое движение твёрдого тела – движение, при котором скорость одной точки тела равна нулю, а остальные точки движутся по сферическим поверхностям, центры которых совпадают с этой неподвижной точкой.
Примером сферического движения тела служит движение волчка, имеющего неподвижную точку О1 (рис. 2.51).
Для определения положения тела в каждый момент времени используют две системы отсчёта: неподвижная система отсчёта O1X1Y1Z1 и подвижная система отсчёта OXYZ, которая жёстко закреплена на теле. При этом начало отсчёта ПСО совпадает с началом отсчёта НСО.
На рис. 2.51 стрелками показаны положительные направления отсчёта углов Ψ, φ, и θ. Рассмотрим подробнее порядок отсчёта этих углов. Плоскость OXY подвижной системы отсчёта OXYZ пересекается с плоскостью O1X1Y1 неподвижной системы отсчёта O1X1Y1Z1 по линии O1L. Эту линию называют осью узлов. Введём единичный вектор р, направленный от точки О1 к точке L оси узлов. Единичные векторы i1, p лежат в горизонтальной плоскости O1X1Y1 и образуют угол Ψ, величина которого зависит от времени. Ψ = f1(t). Положительное направление отсчёта угла Ψ определяют по правилу: смотря навстречу вектору k1, поворот вектора i1 к вектору р должны увидеть происходящим против хода часовой стрелки.
Единичные векторы k1, k образуют плоскость, в которой находится угол θ, который также зависит от времени. θ = f2(t). Положительное направление отсчёта угла θ определяют по правилу: смотря навстречу вектору i, поворот вектора k1, к вектору k должны увидеть происходящим против хода часовой стрелки.
Единичные векторы р, i образуют плоскость, в которой лежит угол φ, величина которого зависти от времени. φ = f3(t). Правило положительного направления отсчёта угла φ: смотря навстречу вектору j, поворот вектора р к вектору i должны увидеть происходящим против хода часовой стрелки.

Углы Ψ, θ, φ называют также эйлеровыми углами:
угол Ψ – угол прецессии;
угол θ – угол нутации;
угол φ – угол собственного вращения.
Так как положение тела, имеющего одну неподвижную точку, определяется тремя эйлеровыми углами, т. е. тремя параметрами, то оно имеет три степени свободы.
Таким образом, сферическое движение тела описывается тремя уравнениями движения:
Ψ = f1(t); θ = f2(t); φ = f3(t).
При сферическом движении широко используют теорему Эйлера-Даламбера.
Твёрдое тело, имеющее одну неподвижную точку, можно переместить из одного положения в другое поворотом вокруг оси, проходящей через неподвижную точку (рис. 2.52).
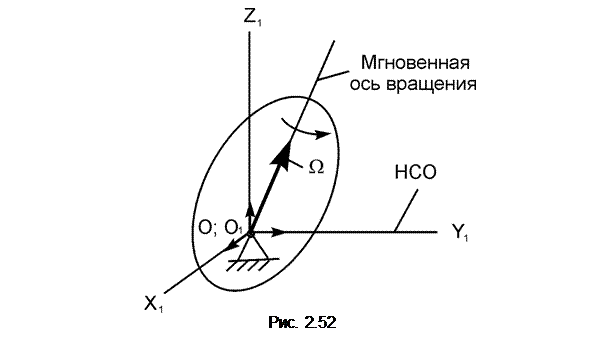 |
Другими словами, тело может вращаться относительно мгновенной оси вращения.
Мгновенная ось вращения – геометрическое место точек тела, скорости которых в данный момент времени равны нулю.
В случае сферического движения вектор угловой скорости Ω в данный момент времени откладывается от неподвижной точки О по мгновенной оси в такую сторону, чтобы, смотря навстречу этому вектору, видеть вращение тела, происходящим против хода часовой стрелки.
Tело, имеющее одну неподвижную точку, можно переместить из одного положения в другое поворотом вокруг некоторой оси, проходящей через неподвижную точку. Примером такого движения является качение подвижного конуса 1 по неподвижному конусу 2 (рис. 2.53). Покажем на рисунке направление вектора мгновенной угловой скорости и запишем формулу для определения модуля скорости точки С подвижного конуса.

Так как скорость VО точки О конуса 1 равна нулю, то этот конус совершает сферическое движение. Такое движение можно представить как вращательное движение относительно мгновенной оси вращения. Мгновенная ось вращения – геометрическое место точек тела, скорости которых в данный момент времени равны нулю. Для тела 1 мгновенной осью вращения является ось ОК (см. рис. 2.53).
Вектор Ω угловой скорости тела 1 откладывается на мгновенной оси вращения в такую сторону, чтобы, смотря навстречу этому вектору, видеть вращение тела, происходящим против хода часовой стрелки.
Модуль VC скорости точки С конуса 1 определяют по формуле
VC = Ω·CL,
где CL – кратчайшее расстояние от точки С тела 1 до мгновенной оси вращения.
Для заочной и дистанционной форм обучения выполнение контрольных работ на сферическое движение не предусмотрено. Однако такие задачи довольно часто встречаются в дидактических единицах интернет–экзамена. Приведём примеры решения задач такого типа.
Пример 1.
Подвижный конус катится по неподвижной горизонтальной плоскости O1X1Y1, имея неподвижную точку О1 (рис. 2.54).
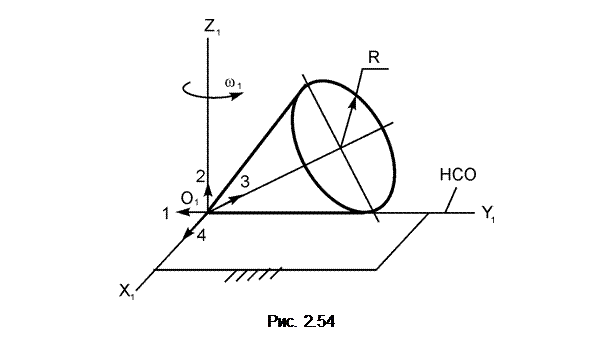
Запишите номер вектора, по которому направлена мгновенная угловая скорость вращения.
Ответ. Мгновенная угловая скорость вращения Ω совпадает с направлением 1.
Пример 2.
Подвижный конус 1 катится без проскальзывания по неподвижному конусу 2, так, что модуль угловой скорости вращения оси О1С относительно оси О1С1 неподвижного конуса постоянен и равен ω1 рад/с (рис. 2.55).
(Для справки: sin(15o) = cos(75o) = 0,26; sin(75o) = cos(15o) = 0,96).
Мгновенная угловая скорость подвижного конуса равна …
Варианты ответов: Ω = 1,9ω1 рад/с; Ω = 2,7ω1 рад/с; Ω = 0,52ω1 рад/с; Ω = 0,35ω1 рад/с; Ω = 0,7ω1 рад/с.
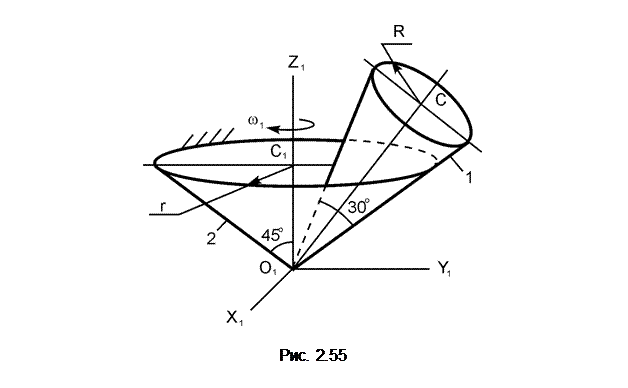
Решение.
Модуль скорости точки С при вращении оси О1С относительно оси О1С1 определим по формуле VC = ω1·CM = ω1·O1C·sin(30o) (рис. 2.56).
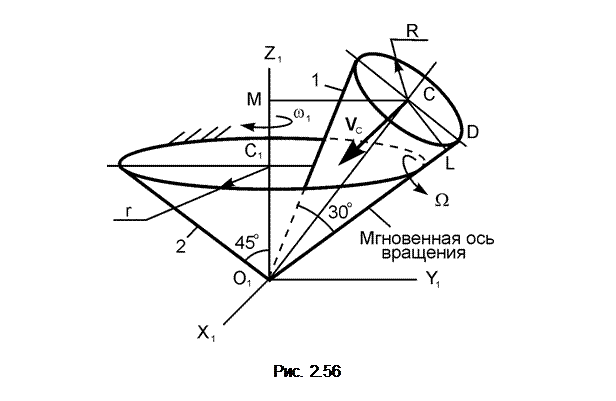
Конус 1 вращается относительно мгновенной оси О1D вращения с угловой скоростью Ω. Исходя из этого, модуль VC скорости точки С конуса 1 равен
VC = Ω·CL = Ω·R·cos(15o) = Ω·(O1C·tg(15o))·cos(15o) =
= Ω·O1C·(sin(15o)/cos(15o))·cos(15o) = Ω·O1C·(sin(15o).
Тогда
VC = ω1·O1C·sin(30o) = Ω·O1C·(sin(15o)).
Решая последнее равенство, получим
Ω = ω1·(sin(30o)/sin(15o)) = ω1·(0,5/0,26) = 1,93 рад/с.
Правильный ответ: Ω = 1,93 рад/с.
Пример 3.
Подвижный конус 1 катится без проскальзывания по неподвижному конусу 2, так, что модуль угловой скорости вращения оси ОС относительно оси ОС1 неподвижного конуса постоянен и равен ω1 рад/с (рис. 2.57).
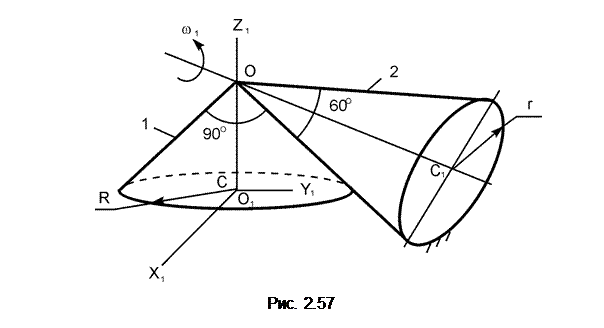
(Для справки: sin(15o) = cos(75o) = 0,26; sin(75o) = cos(15o) = 0,96).
Если известны углы и радиус основания R = 1 м, то мгновенная угловая скорость подвижного конуса 1 равна …
Варианты ответов: Ω = 0,73·ω1 рад/с; Ω = 0,52·ω1 рад/с; Ω = 0,28·ω1 рад/с; Ω = 1,37·ω1 рад/с; Ω = 1,92·ω1 рад/с.
Решение.
Модуль скорости точки С при вращении оси ОС относительно оси ОС1 определим по формуле VC = ω1·CM = ω1·OC·sin(75o) (рис. 2.58).
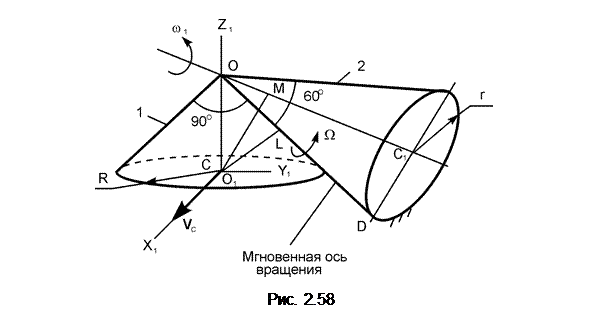
Конус 1 вращается относительно мгновенной оси О1D вращения с угловой скоростью Ω. Исходя из этого, модуль VC скорости точки С конуса 1 равен
VC = Ω·CL = Ω·(OC)·sin(45o).
Тогда
VC = ω1·OC·sin(75o) = Ω·OC·sin(75o).
Решая последнее равенство, получим
Ω = ω1·(sin(75o)/sin(45o)) = ω1·(0,96/0,707) = 1,37·ω1 рад/с.
Правильный ответ: Ω = 1,37·ω1 рад/с.
2.29. Общий случай движения твёрдого тела
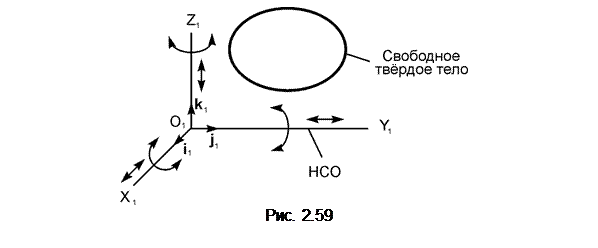 |
Рассмотрим движение свободного твёрдого тела в неподвижной системе отсчёта OXYZ (рис. 2.59).
В общем случае движение свободного тела в пространстве можно рассматривать как сумму простейших движений (три поступательных движения, параллельные координатным осям, и три вращательных движения относительно этих осей), которые осуществляются одновременно и независимо друг от друга.
Таким образом, свободное тело в пространстве имеет шесть степеней свободы.
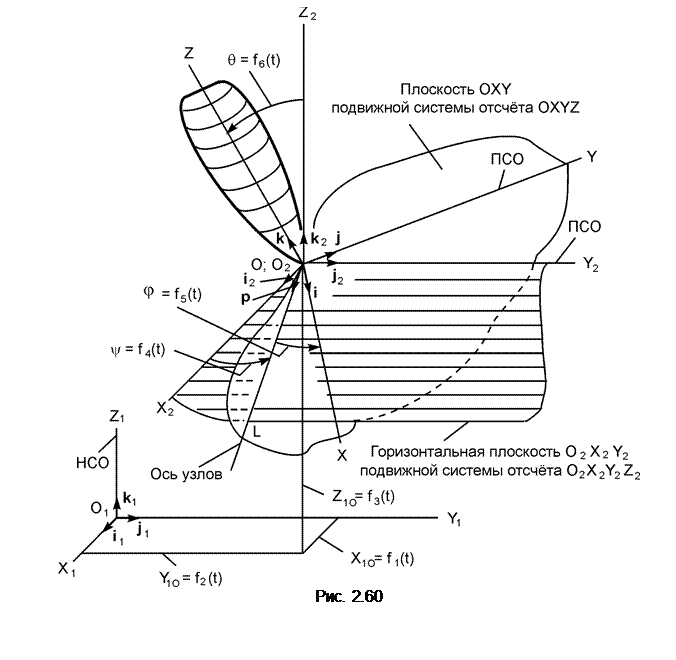
В теоретической механике движение свободного тела в пространстве рассматривают как сложное, состоящее из поступательного движения со скоростью некоторой точки тела, принятой за полюс, и сферического движения вокруг этого полюса (рис. 2.60).
Примем произвольную точку О за полюс и поместим в него начала двух подвижных систем отсчёта OXYZ, O2X2Y2Z2. При этом система отсчёта OXYZ неподвижно закреплена на теле, а система отсчёта O2X2Y2Z2 совершает поступательное движение таким образом, что её координатные оси параллельны координатным осям неподвижной системы отсчёта O1X1Y1Z1.
Плоскости OXY, O2X2Y2 подвижных систем отсчёта пересекаются по линии OL. Введением единичного вектора р эту линию преобразуют в ось узлов.
На рис. 2.60 показаны углы Ψ, φ, θ, величины которых зависят от времени. Эти углы называют эйлеровыми углами.
Таким образом, свободное движение тела определяется шестью уравнениями движения свободного твёрдого тела.
X1О = f1(t); Y1О = f2(t); Z1О = f3(t);
Ψ = f4(t); φ = f5(t); θ = f6(t),
где X1О, Y1О, Z1О – координаты полюса О в неподвижной системе отсчёта O1X1Y1Z1.
Первые три уравнения, определяющие поступательную часть движения тела, зависят от выбора полюса О, так как координаты различных точек тела различны.
Остальные три уравнения, определяющее сферическое движение тела вокруг полюса, от выбора полюса не зависят.
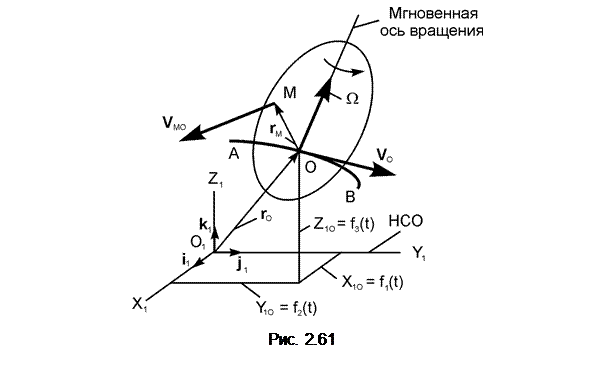 |
В технических расчётах движение свободного тела рассматривают также как вращательное движение относительно мгновенной оси вращения, проходящей через подвижный полюс (рис. 2.61).
Скорость VM любой точки М свободного тела равна геометрической сумме скорости VO полюса О и скорости VMO этой точки в её сферическом движении вокруг полюса.
VM = VO + VMO.
Скорость VMO определяют по формуле
VMO = Ω × rM,
где Ω – вектор мгновенной угловой скорости; rM – радиус-вектор, начало которого находится в полюсе, а конец в точке М.
Для студентов заочной и дистанционной форм обучения выполнение курсовых заданий на свободное движение тела не предусмотрено.
Вопросы и задания для самоконтроля
1. Сформулировать определение термина «сложное движение точки или тела».
2. Сформулировать определение термина «абсолютное движение точки».
3. Сформулировать определение термина «относительное движение точки».
4. Сформулировать определение термина «переносное движение точки».
5. Сформулировать определение термина «абсолютная траектория точки».
6. Сформулировать определение термина «относительная траектория точки».
7. Сформулировать определение термина «абсолютная скорость точки».
8. Сформулировать определение термина «относительная скорость точки».
9. Сформулировать определение термина «переносная скорость точки».
10. Сформулировать определение термина «абсолютное ускорение точки».
11. Сформулировать определение термина «относительное ускорение точки».
12. Сформулировать определение термина «переносное ускорение точки».
13. Сформулировать определение термина «кориолисово ускорение точки».
СЛОВАРЬ
ТЕРМИНОВ, ОПРЕДЕЛЕНИЙ, ПОНЯТИЙ
Кинематика – раздел механики, в котором изучаются движения материальных тел без учёта их масс и действующих на них сил. Примечание. В кинематике движущиеся объекты рассматриваются как геометрические… Основная система отсчёта – при рассмотрении движения тел по отношению к нескольким системам отсчёта – та из этих…ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ…….……………………………………………….……………………………3
ПРОГРАММА ДИСЦИПЛИНЫ «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА»
(разделы «Статика», «Кинематика»)… ……………………….…………….………….6
ОБЩИЕ ПОЛОЖЕНИЯ…………………………………………….……….……………..8
ПРОГРАММА РАЗДЕЛА «СТАТИКА»……………………………………….…………10
ПРОГРАММА РАЗДЕЛА «КИНЕМАТИКА»………………………………..…………..12
РАЗДЕЛ ПЕРВЫЙ………………………………………………………………………..15
1. СТАТИКА………………………………………………………………………………..15
1.1. Основные понятия статики……………………..……………………………….15
1.2. Аксиомы статики………………………………..…………………………………24
Вопросы и задания для самоконтроля…………………….…………………28
1.3. Связи и реакции связей……………………………..……………….......................30
Вопросы и задания для самоконтроля……………………….……………….36
1.4. Проекции силы на ось и плоскость…………………..…………….................36
1.5. Аналитический способ сложения сил……………….……….………………..40
1.6. Аналитические условия равновесия системы
сходящихся сил………………………………………………….…..…………….43
1.7. Алгоритм решения задач статики……………………….……………………..43
1.8. Пример решения задачи на плоскую
сходящуюся систему сил………………………………………………………...44
Вопросы и задания для самоконтроля…………………….………………....46
1.9. Пара сил……………………………………..……………………..………………46
1.10. Сложение пар сил…………………………………..……………..…………...49
1.11. Условия равновесия пар сил……………………….……….........................50
1.12. Вектор момента силы относительно точки……………….……..................51
1.13. Алгебраический момент силы относительно точки……….….…………......51
Вопросы и задания для самоконтроля…………………………..………....53
1.14. Приведение силы к заданному центру
(метод Пуансо)…………….………………….…..……………………………..54
1.15. Приведение произвольной системы сил
к заданному центру……………………………………………………………..55
1.16. Аналитические условия равновесия
плоской произвольной системы сил…………………………...…………….56
1.17. Другие типы связей на плоскости………………………..……….................59
1.18. Варианты курсового задания С 1
«Определение реакций опор твёрдого тела»….………..………………....61
1.19. Пример выполнения курсового задания С 1………………………………..70
Вопросы и задания для самоконтроля……………………….……………..72
1.20. Расчет фермы……………………………………….…………………………..73
1.21. Методология расчета усилий в стержнях
плоской фермы…………………………………………………………………..74
1.21.1. Варианты курсового задания С2
«Определение реакций опор
и сил в стержнях плоской фермы»…………..…………….………...74
1.21.2. Аналитический и графический способы
вырезания узлов……………….………….….………………………...82
1.21.3. Определение усилий в стержнях фермы
способом Риттера………………………………………………………87
Вопросы и задания для самоконтроля…….……………………...90
1.22. Определение реакций опор составных конструкций….…………………..906
1.23. Алгоритм решения задач на определение реакций
внешних связей для составных конструкций…………………….………...92
1.24. Варианты курсового задания С 3
«Определение реакций опор составной конструкции
(система двух тел)»………………………….….……………………………….93
1.25. Пример выполнения курсового задания С 3………………….…………...101
Вопросы и задания для самоконтроля………………………….…………106
1.26. Пространственная произвольная система сил……………..………….…107
1.26.1. Момент силы относительно оси………….………….……………..107
1.26.2. Аналитические выражения моментов силы
относительно координатных осей………………………………....108
1.26.3. Приведение пространственной произвольной
системы сил к заданному центру………………….………………..109
1.26.4. Уравнения равновесия пространственной
системы сил……………………………………..…………………..…111
1.26.5. Типы связей в пространстве……………………………................112
1.27. Варианты курсового задания С 4
«Определение реакций опор твёрдого тела»…………………………….113
1.28. Пример выполнения курсового задания С 4……………………………….123
Вопросы и задания для самоконтроля……………………….…………..125
1.29. Сцепление и трение скольжения………………………………………..…125
1.30. Центр тяжести твёрдого тела………………………………………………130
Словарь терминов, определений, понятий
(по разделу «Статика»)……………………..….…………………………….138
РАЗДЕЛ ВТОРОЙ……………………………………………………………………….142
2. КИНЕМАТИКА………………………………….…….............................................142
2.1. Введение в кинематику……..…………………..………….………………..…142
2.2. Координатный способ задания движения точки………….…………….….142
2.3. Скорость точки……….……………………………..…………………………...146
2.4. Ускорение точки………………………………………..………………………..148
2.5. Естественный способ задания движения точки…………..………………..152
2.6. Естественные координатные оси………………………………………….…153
2.7. Скорость точки……………………………..………………….…..…………….156
2.8. Ускорение точки..…………………………………..……………………………156
2.9. Классификация движения точки
по ускорениям ее движения…………………………………..…………….…158
2.10. Связь координатного и естественного
способов задания движения точки……………………………….………....158
2.11. Векторный способ задания движения точки……….……………………..159
2.12. Варианты курсового задания К 1
«Определение скорости и ускорения точки
по заданным уравнениям её движения»………………..……….…………161
2.13. Пример выполнения курсового задания К 1..…………….…………….…162
Вопросы и задания для самоконтроля………………………………….…166
2.14. Поступательное движение твердого тела…………….…………………..169
2.15. Вращательное движение твердого тела…………………………………..171
2.16. Варианты курсового задания К 2
«Определение скоростей и ускорений точек
твердого тела при поступательном
и вращательном движениях»……..………………………………............178
2.17. Пример выполнения курсового задания К 2………….…………………...188
2.18. Плоскопараллельное движение твёрдого тела..……….………………..190
2.19. Определение скоростей точек тела
с помощью мгновенного центра скоростей…………………………….…195
2.20. Различные случаи определения положения
мгновенного центра скоростей………………………………...…………....196
2.21. Варианты курсового задания К 3
«Кинематический анализ плоского механизма»………….….…………...199
2.22. Пример выполнения курсового задания К 3…………….…………………207
Вопросы и задания для самоконтроля…………………….………….…..209
2.23. Сложное движение точки………………………..………….….…………….211
2.24. Сложение скоростей……………………………………….……..…………..216
2.25. Сложение ускорений (теорема Кориолиса)…………….…………………217
2.26. Варианты курсового задания К 4
«Определение абсолютной скорости
и абсолютного ускорения точки»….………………………….…………….221
2.27. Пример выполнения курсового задания К 4……………………………….230
2.28. Сферическое движение твёрдого тела…………………………………….236
2.29. Общий случай движения твёрдого тела…………………………………...243
Вопросы и задания для самоконтроля……………………………………246
Словарь терминов, определений, понятий
(по разделу «Кинематика»)…………..……………………………………...247
Для заметок
Для заметок
Учебное издание
Александр Михайлович Лукин
Денис Александрович Лукин
Владимир Васильевич Квалдыков
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
Учебно-методическое пособие
***
Редактор Т. И. Калинина
***
Подписано к печати . Формат 60х90 1/16. Бумага писчая
Гарнитура Arial. Оперативный способ печати
Усл. п. л. 16,0. уч.- изд. л. 16,0. Тираж 400 экз. Заказ №
Цена договорная
***
Издательство СибАДИ
644099, Омск, ул. П. Некрасова, 10
 |
Отпечатано в типографии
ООО «Принт сервис»
644043, Омск, Гагарина 8/1
– Конец работы –
Используемые теги: Теоретическая, Механика0.04
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов