рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Учебное пособие предназначено для студентов гуманитарных специальностей, изучающих математику по технологии индивидуализированного обучения
Реферат Курсовая Конспект
Учебное пособие предназначено для студентов гуманитарных специальностей, изучающих математику по технологии индивидуализированного обучения
Учебное пособие предназначено для студентов гуманитарных специальностей, изучающих математику по технологии индивидуализированного обучения - раздел Математика, Введение Учебное Пособие П...
Введение
Учебное пособие предназначено для студентов гуманитарных специальностей, изучающих математику по технологии индивидуализированного обучения. Оно содержит в полном объеме предназначенный для изучения теоретический материал в соответствии с Государственным образовательным стандартом и рабочей программой, задачи для самостоятельного решения, вопросы к экзамену (зачету), темы рефератов, памятку для студентов, задания контрольной работы для студентов заочного отделения, примерный вариант решения этой контрольной работы и список дополнительной литературы.
Теоретический материал был отобран из учебников по математике для гуманитарных специальностей, научно-популярной литературы, методически обработан для самостоятельного изучения и содержит большое количество примеров, поясняющих теорию и помогающих в дальнейшем в решении задач.
Задачи для самостоятельного решения разбиты на два уровня сложности: основной и повышенный. Задачи основного уровня сложности составлены по аналогии с примерами, имеющимися в теоретическом материале соответствующей темы. В задачах повышенного уровня сложности требуется предварительный анализ по распознаванию задачи и приведению ее к стандартному виду. Задачи сгруппированы по темам и по типам. Это позволяет преподавателю составлять не менее 10 вариантов карточек для самостоятельной работы основного уровня и не менее 5 вариантов повышенного уровня по каждой теме.
Перед началом работы с пособием студенту необходимо внимательно ознакомиться с памяткой. В ней указан алгоритм изучения каждой темы. Темы можно изучать в произвольном порядке, кроме тем «Элементы комбинаторики» и «Элементы теории вероятностей». Вторая тема изучается после первой, так как использует формулы и определения, сформулированные в теме «Элементы комбинаторики».
ПАМЯТКА СТУДЕНТУ
Я слышу – и забываю,
Я вижу – и запоминаю,
Я делаю – и понимаю.
Конфуций
Весь теоретический материал курса разбит на порции по темам и сопровождается задачами двух уровней сложности. Работа по усвоению нового учебного… Каждый студент имеет возможность работать в индивидуальном режиме и изучать… 1 Прочитать теоретический материал.П.Дирак
Если теорему так и не смогли доказать – она становится аксиомой.
Евклид
Сущность аксиоматического метода
Математика строится на основе понятий. Понятия бывают определяемые и неопределяемые. Под определением понимают точную формулировку того или иного… Пример 1. Определение: «Квадрат – это прямоугольник, у которого все стороны… Существуют понятия, которые нельзя определить через другие, более общие понятия. Их в математике называют основными…Пример 2.
Аксиома: «Какова бы ни была прямая, существуют точки, принадлежащие этой прямой и точки, не принадлежащие ей». [10]
Теорема: «Если диагонали четырехугольника пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм». [10]
Одним из основных методов современной математики является аксиоматический метод. Сущность его состоит в следующем:
1) перечисляются основные неопределяемые понятия и отношения строящейся теории (примеры отношений: следовать за..., лежать между...);
2) формулируются аксиомы, принимаемые в данной теории без доказательства, которые выражают связь между основными понятиями и их отношениями;
3) предложения, которых нет среди основных понятий и основных отношений, должны быть определены;
4) предложения, которых нет в списке аксиом, должны быть доказаны на основе этих аксиом и ранее доказанных предложений.
1.2 Геометрия Евклида – первая естественно научная теория
Исторический обзор обоснования геометрии.Геометрия, прежде чем стать аксиоматической теорией, прошла долгий путь эмпирического развития.
Первые сведения о геометрии были получены цивилизациями Древнего Востока (Египет, Китай, Индия) в связи с развитием земледелия, ограниченностью плодородных земель и др. В этих странах геометрия носила эмпирический характер и представляла собой набор отдельных «рецептов-правил» для решения конкретных задач. Уже во II тысячелетии до н.э. египтяне умели точно вычислить площадь треугольника, объем усеченной пирамиды, площадь круга, а вавилоняне знали теорему Пифагора. Заметим, что доказательств не было, а указывались правила для вычислений.
Греческий период развития геометрии начался в VII-VI вв. до н.э. под влиянием египтян. Отцом греческой математики считается знаменитый философ Фалес (640-548 гг. до н.э.). Фалесу, точнее, его математической школе принадлежат доказательства свойств равнобедренного треугольника, вертикальных углов. В дальнейшем геометром Древней Греции были получены результаты, охватывающие почти все содержание современного школьного курса геометрии.
Философская школа Пифагора (570-471 гг. до н.э.) открыла теорему о сумме углов треугольника, доказала теорему Пифагора, установила существование пяти типов правильных многогранников и несоизмеримых отрезков. Демокрит (470-370 гг. до н.э.) открыл теоремы об объемах пирамиды и конуса. Евдокс (410-356 гг. до н.э.) создал геометрическую теорию пропорций (т.е. теорию пропорциональных чисел).
Менехм и Аполлоний изучили конические сечения. Архимед (289-212 гг. до н.э.) открыл правила вычисления площади поверхности и объема шара и других фигур. Он же нашел приближенное значение числа π.
Особая заслуга древнегреческих ученых состоит в том, что они первыми поставили задачу строгого построения геометрических знаний и решили ее в первом приближении. Проблему поставил Платон (428-348 гг. до н.э.). Аристотелю (384-322 гг. до н.э.) – крупнейшему философу, основателю формальной логики – принадлежит четкое оформление идеи построения геометрии в виде цепи предложений, которые вытекают одно из другого на основе лишь правил логики. Эту задачу пытались решить многие греческие ученые (Гиппократ, Федий).
Евклид (330-275 гг. до н. э.) – крупнейший геометр древности, воспитанник школы Платона, жил в Египте (в Александрии). Составленные им «Начала» дают систематическое изложение начал геометрии, выполненное на таком научном уровне, что многие века преподавание геометрии велось по его сочинению. «Начала» состоят из 13 книг (глав):
I-VI – планиметрия;
VII-IХ – арифметика в геометрическом изложении;
X – несоизмеримые отрезки;
ХI-ХII – стереометрия.
В «Начала» были включены не все сведения, известные в геометрии. Например, в эти книги не вошли: теория конических сечений, кривые высших порядков.
Каждая книга начинается с определения тех понятий, которые в ней встречаются. Например, в книге I даны 23 определения. Приведем определения первых четырех понятий:
1 Точка есть то, что не имеет частей.
2 Линия есть длина без ширины.
3 Границы линии суть точки.
4 Прямая есть такая линия, которая одинаково расположена по отношению ко всем своим точкам.
Евклид приводит предложения, принимаемые без доказательства, разделяя их на постулаты и аксиомы. Постулатов у него пять, а аксиом – семь. Вот некоторые из них:
IV И чтобы все прямые углы были равны.
V И чтобы всякий раз, когда прямая при пересечении с двумя другими прямыми образует с ними внутренние односторонние углы, сумма которых меньше двух прямых, эти прямые пересекались с той стороны, с которой эта сумма меньше двух прямых.
Аксиомы
I Равные порознь третьему равны между собой.
II И если к равным прибавить равные, то получим равные.
VII И совмещающиеся равны.
Евклид не указал, в чем заключается различие между постулатами и аксиомами. До сих пор нет окончательного решения этого вопроса.
Евклид излагает теорию геометрии так, как требовали греческие ученые, особенно Аристотель, т.е. теоремы расположены так, что каждая следующая доказывается только на основе предыдущих. Иначе говоря, Евклид развивает геометрическую теорию строго логическим путем. В этом и заключается историческая заслуга Евклида перед наукой.
«Начала» Евклида сыграли огромную роль в истории математики и всей человеческой культуры. Эти книги переведены на все основные языки мира, после 1482 г. они выдержали около 500 изданий.
Недостатки системы Евклида. С точки зрения современной математики изложение «Начал» следует признать несовершенным. Назовем основные недостатки этой системы:
1) многие понятия включают такие, которые в свою очередь должны быть определены (например, в определениях 1-4 главы 1 используются понятия ширины, длины, границы, которые также должны быть определены);
2) список аксиом и постулатов недостаточен для построения геометрии строго логическим путем. Например, в этом списке нет аксиом порядка, без которых нельзя доказать многие теоремы геометрии; заметим, что на это обстоятельство обратил внимание Гаусс. В указанном списке отсутствуют также определения понятия движения (совмещения) и свойств движения, т.е. аксиом движения. В списке не хватает также аксиомы Архимеда (одной из двух аксиом непрерывности), которая играет важную роль в теории измерений длин отрезков, площадей фигур и объектов тел. Заметим, что на это обратил внимание современник Евклида Архимед;
3) постулат IV явно лишний, его можно доказать как теорему. Особо отметим пятый постулат. В книге I «Начал» первые 28 предложений доказаны без ссылок на пятый постулат. Попытка минимизировать список аксиом и постулатов, в частности доказать постулат V как теорему, проводилась со времен самого Евклида. Прокл (V в. н. э.), Омар Хайям (1048-1123 гг.), Валлис (XVII в.), Саккери и Ламберт (XVIII в.), Лежандр (1752-1833 гг.) также пытались доказать постулат V как теорему. Их доказательства были ошибочными, но они привели к положительным результатам – к рождению еще двух геометрий (Римана и Лобачевского).
Неевклидовы геометрические системы.Н.Лобачевский (1792-1856 гг.), который открыл новую геометрию – геометрию Лобачевского, также начал с попытки доказательства постулата V.
Николай Иванович развил свою систему до объема «Начал» в надежде получить противоречие. Не получил, но сделал в 1826 г. правильный вывод: существует геометрия, отличная от геометрии Евклида.
На первый взгляд этот вывод кажется недостаточно обоснованным: может быть, развивая его дальше, можно прийти к противоречию. Но этот же вопрос относится и к геометрии Евклида. Иначе говоря, обе геометрии равноправны перед вопросом о логической непротиворечивости. Дальнейшие исследования показали, что из непротиворечивости одной следует непротиворечивость другой геометрии, т.е. имеет место равноправие логических систем.
Лобачевский был первым, но не единственным, кто сделал вывод о существовании другой геометрии. Гаусс (1777-1855 гг.) высказал эту идею еще в 1816 г. в частных письмах, но в официальных публикациях заявление не сделал.
Три года спустя после публикации результатов Лобачевского (в 1829 г.), т.е. в 1832 г., вышла работа венгра Я. Бойяи (1802-1860 гг.), который в 1823 г. пришел к выводу о существовании другой геометрии, но опубликовал позже и в менее развитом, чем у Лобачевского, виде. Поэтому справедливо, что эта геометрия носит имя Лобачевского.
Общему признанию геометрии Лобачевского в значительной степени способствовали работы геометров после Лобачевского. В 1868 г. итальянский математик Э.Бельтрами (1825-1900 гг.) доказал, что на поверхности постоянной отрицательной кривизны (так называемая псевдосфера) имеет место геометрия Лобачевского. Уязвимым местом доказательства непротиворечивости геометрии Лобачевского, основанного на интерпретации Бельтрами, было то, что, как показал Д.Гильберт (1862-1943 гг.), в евклидовом пространстве не существует полной поверхности постоянной отрицательной кривизны без особенностей. Поэтому на поверхности постоянной отрицательной кривизны можно интерпретировать только часть плоской геометрии Лобачевского. Этот недостаток был устранен А.Пуанкаре (1854-1912 гг.) и Ф.Клейном (1849-1925 гг.).
Доказательство непротиворечивости геометрии Лобачевского было вместе с тем и доказательством независимости пятого постулата от остальных. Действительно, в случае зависимости геометрия Лобачевского была бы противоречивой, так как она содержала бы два взаимно исключающих утверждения.
Дальнейшие исследования евклидовой геометрии показали неполноту системы аксиом и постулатов Евклида. Исследование аксиоматики Евклида завершил в 1899 г. Гильберт.
Аксиоматика Гильберта состоит из пяти групп:
• аксиомы связи (принадлежности);
• аксиомы порядка;
• аксиомы конгруэнтности (равенства, совпадения);
• аксиомы непрерывности;
• аксиома параллельности.
Эти аксиомы (всего их 20) относятся к объектам трех родов: точек, прямых, плоскостей, а также к трем отношениям между ними: «принадлежит», «лежит между», «конгруэнтен». Конкретный смысл точек, прямых, плоскостей и отношений не указан. Они косвенно определены через аксиомы. Благодаря этому построенная на основе аксиом Гильберта геометрия допускает различные конкретные реализации.
Геометрическая система, построенная на перечисленных аксиомах, называется евклидовой геометрией, так как совпадает с геометрией, изложенной Евклидом в «Началах».
Геометрические системы, отличные от евклидовой, называются неевклидовыми геометриями. Согласно общей теории относительности, в пространстве ни та, ни другая не являются абсолютно точными, однако в малых масштабах (земные масштабы являются также достаточно «малыми») они вполне пригодны для описания пространства. Причиной того, что на практике применяются евклидовы формулы, является их простота.
Гильберт всесторонне исследовал свою систему аксиом, показал, что она непротиворечива, если не противоречива арифметика (т.е. на самом деле доказана содержательная или так называемая внешняя непротиворечивость). Он завершил многовековые исследования геометров по обоснованию геометрии. Эта работа была высоко оценена и в 1903 г. отмечена премией имени Лобачевского.
В современном аксиоматическом изложении геометрии Евклида не всегда пользуются аксиомами Гильберта: учебники по геометрии построены на различных модификациях этой системы аксиом.
В XX в. было обнаружено, что геометрия Лобачевского не только имеет важное значение для абстрактной математики как одна из возможных геометрий, но и непосредственно связана с приложениями математики. Оказалось, что взаимосвязь пространства и времени, открытая А.Эйнштейном и другими учеными в рамках специальной теории относительности, имеет непосредственное отношение к геометрии Лобачевского.
Предмет математики
Предмет математики нельзя ни подменять формальными логическими схемами, ни низводить до уровня коллекции разрозненных фактов. Математика есть учение… Известны два подхода к определению предмета математики. Одно определение дано… Согласно Ф. Энгельсу, «чистая математика имеет своим объектом пространственные формы и количественные отношения…Место и роль математики в современном мире, мировой культуре и истории, в том числе в гуманитарных науках
Роль математики в общечеловеческой культуре огромна. Обращаясь к истории философии, следует отметить, что ученые, создававшие математику Нового… Место математики в жизни и в науке определяется тем, что она позволяет…М. Стоун
Основные понятия теории множеств
В конце XIX века в математической науке возникла необходимость уточнить смысл таких ведущих понятий, как функция, непрерывность и т. д. Для этого нужно было строго определить, что такое натуральное число. Поиски ответа на эти сложные вопросы способствовали развитию новых математических идей, поэтому в конце XIX начале XX столетий происходил пересмотр старых представлений буквально во всех областях математических знаний. В результате в конце XIX века возникла новая область математики – теория множеств, одним из создателей которой был немецкий математик Георг Кантор (1845 – 1918). За небольшой срок теория множеств стала фундаментом всей математики.
Понятие множества является ключевым в математике, без которого невозможно изложение ни одного из ее разделов. Подсознательно первые представления о множестве у человека начинают формироваться с рождения, когда он погружается в многообразный мир окружающих его объектов и явлений. С первых же шагов мы не просто пополняем список знакомых нам объектов и явлений, а начинаем дифференцировать и классифицировать (горячие и холодные, сладкие и горькие, тяжелые и легкие и т. п.), объединяя тем самым объекты в некоторые совокупности.
В математике понятие «множество» используется для описания предметов или объектов. При этом предполагается, что предметы (объекты) данной совокупности можно отличить друг от друга и от предметов, не входящих в эту совокупность.
Создатель теории множеств Г. Кантор определил множество как «объединение в одно целое объектов, хорошо различимых нашей интуицией или мыслью», а также «множество есть многое мыслимое нами как единое». Эти слова не могут рассматриваться как математически строгое определение множества, такого определения не существует. Понятие множества относится к исходным (не определяемым), на основании которых строятся остальные понятия математики.
Множество – это совокупность каких-либо объектов. Так, можно говорить о множестве всех книг данной библиотеки, множестве всех вершин данного многоугольника, множестве всех натуральных чисел, множестве всех точек данной прямой и т. д. Объекты, входящие в данное множество называются элементами множества. Книги данной библиотеки, вершины данного многоугольника, натуральные числа, точки данной прямой являются элементами соответствующих множеств.
Множества обычно обозначаются большими буквами A, B, X, а их элементы – малыми буквами а, b, x.
Множество называется конечным, если количество его элементов можно выразить целым неотрицательным числом (причем неважно, известно это число или нет, главное, оно существует), в противном случае множество называется бесконечным.
Пример 1. Множество книг в библиотеке, множество студентов в группе являются конечными. Множество натуральных чисел, множество точек прямой являются бесконечными.
Количество элементов множества обозначается |A|.
Пример 2. Пусть В – множество правильных многоугольников. Тогда В = {тетраэдр, куб, октаэдр, додекаэдр, икосаэдр}. |B| = 5.
Запись x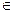 Х, означает что объект х есть элемент множества Х, читается «х принадлежит множеству Х», «х входит в множество Х». Если х не принадлежит множеству Х, то пишут х
Х, означает что объект х есть элемент множества Х, читается «х принадлежит множеству Х», «х входит в множество Х». Если х не принадлежит множеству Х, то пишут х  Х.
Х.
Например, если через Nобозначим множество натуральных чисел, то 3 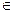 N,20
N,20 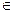 N,0
N,0  N,
N, 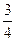
 N.
N.
Если все элементы множества А принадлежат какому-то множеству В, то говорят, что множество А является подмножеством множества В. Записывают А 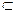 В (множество А содержится во множестве В). Любое множество является подмножеством самого себя, т. е. справедливо утверждение А
В (множество А содержится во множестве В). Любое множество является подмножеством самого себя, т. е. справедливо утверждение А 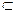 А.
А.
Если множество не содержит ни одного элемента, то его называют пустым и обозначают символом Ø. Пустое множество является подмножеством любого множества.
Подмножества, которые содержат не все элементы множества В, называют собственными подмножествами множества В.
Пример 3. Дано множество М = {a; c; m}. Найти все его подмножества.
Решение:
M1 = {a}, M2 = {c}, M3 = {m}, M4 = {a; c}, M5 = {a; m}, M6 = {c; m}, M7 = {a; c; m}, M8 = Ø.
Множества M7 и M8 называются несобственными подмножествами множества М.
Множества А и В называют равными (А = В), если они состоят из одних и тех же элементов,т.е. В 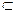 А и А
А и А 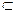 В.
В.
Например, множества А = {3, 5, 7, 9} и В = {7, 3, 9, 5} равны, т. к. состоят из одинаковых элементов.
Множества, элементами которых являются числа, называются числовыми. Примерами числовых множеств являются:
Ν={1; 2; 3; ...; n; ...} – множество натуральных чисел (чисел, которые используют при счете предметов);
Ζ0={0; 1; 2; ...; n; ...} – множество целых неотрицательных чисел;
Ζ={0; ±1; ±2; ...; ±n; ...} – множество целых чисел (натуральные числа и им противоположные);
Q={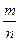 : m
: m 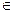 Z, n
Z, n 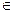 N} – множество рациональных чисел (числа, которые можно представить в виде обыкновенной дроби: целые числа, конечные десятичные и бесконечные десятичные периодические дроби);
N} – множество рациональных чисел (числа, которые можно представить в виде обыкновенной дроби: целые числа, конечные десятичные и бесконечные десятичные периодические дроби);
R – множество действительных чисел (рациональные и иррациональные, т.е. бесконечные десятичные непериодические дроби).
Между этими множествами существует соотношение: 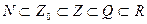 .
.
Множество R содержит рациональные и иррациональные числа. Всякое рациональное число выражается или конечной десятичной дробью, или бесконечной периодической дробью. Так, ½=0,5 (=0,5000…), ⅓=0,333… – рациональные числа.
Действительные числа, не являющиеся рациональными, называются иррациональными. Иррациональное число выражается бесконечной непериодической дробью. Например,  = 1,4142356…, π = 3,1415926… – иррациональные числа.
= 1,4142356…, π = 3,1415926… – иррациональные числа.
Способы задания множеств
Понятие множества мы используем без определения. Но как узнать, является та или иная совокупность множеством или не является?
Считают, что множество определяется своими элементами, т.е. множество задано, если о любом объекте можно сказать, принадлежит он этому множеству или не принадлежит.
Множество можно задать, перечислив все его элементы. Например, если мы скажем, что множество А состоит из чисел 3, 4, 5, и 6, то мы задали это множество, поскольку все его элементы окажутся перечисленными. При этом возможна запись, в которой перечисляемые элементы заключаются в фигурные скобки: А = {3, 4, 5, 6}.
Однако если множество бесконечно, то его элементы перечислить нельзя. Трудно задать таким способом и конечное множество с большим числом элементов. В таких случаях применяют другой способ задания множества: указывают характеристическое свойство его элементов.
Характеристическое свойство – это такое свойство, которым обладает каждый элемент, принадлежащий множеству, и не обладает ни один элемент, который ему не принадлежит.
Рассмотрим, например, множество А двузначных чисел: свойство, которым обладает каждый элемент данного множества, – «быть двузначным числом». Это характеристическое свойство дает возможность решать вопрос о том, принадлежит какой-либо объект множеству А или не принадлежит. Так, число 45 содержится в множестве А, поскольку оно двузначное, а число 145 множеству А не принадлежит, так как оно не является двузначным.
Случается, что одно и то же множество можно задать, указав различные характеристические свойства его элементов. Например, множество квадратов можно задать как множество прямоугольников с равными соседними сторонами и как множество ромбов с прямым углом.
В тех случаях, когда характеристическое свойство элементов множества можно представить в символической форме, возможна соответствующая запись множества. Например, множество А натуральных чисел, меньших 7, можно задать так: А = {х| х 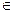 N и х < 7}. При такой записи буквой х обозначается элемент множества А. Для этих целей можно использовать и другие буквы латинского алфавита.
N и х < 7}. При такой записи буквой х обозначается элемент множества А. Для этих целей можно использовать и другие буквы латинского алфавита.
Пример 4. Даны множества: М = {2; 3; 5; 7}, N = {-5; -4; -3; -2}, F = {x| x 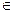 Z, -6 < x < -1}, D = {x| x
Z, -6 < x < -1}, D = {x| x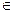 N, x < 10, x – простое число}. Какие множества равны между собой?
N, x < 10, x – простое число}. Какие множества равны между собой?
Решение: Множества F и D заданы характеристическими свойствами. Для того, чтобы сравнить их между собой и с остальными множествами, сформулируем их характеристические свойства словами, а затем зададим их перечислением элементов.
F – множество целых чисел, больших «-6» и меньших «-1». Этому свойству удовлетворяют числа -5, -4, -3, и -2. Из этих чисел состоит множество N. Значит, F = N.
D – множество натуральных чисел, которые меньше 10 и являются простыми. Этому свойству удовлетворяют числа 2, 3, 5 и 7. Из этих чисел состоит множество M. Следовательно, D = M.
Операции над множествами
Пересечение множеств
Рассмотрим два множества: Х = {0, 1, 3, 5}, Y = {1, 2, 3, 4}. Числа 1 и 3 и только они принадлежат одновременно обоим множествам Х и Y.… Множество, состоящее из всех элементов, принадлежащих и множеству А, и множеству В, называется пересечением множеств А…Объединение множеств
Вновь возьмём множества Х = {0, 1, 3, 5} и Y = {1, 2, 3, 4} и наряду с ними рассмотрим множество {0, 1, 2, 3, 4, 5}. Это множество содержит все… Множество, состоящее из всех элементов, принадлежащих или множеству А или… Итак, {0, 1, 3, 5} {1, 2, 3, 4} = {0, 1, 2, 3, 4, 5}.Вычитание множеств
Если заданы два множества, то можно не только найти их пересечение и объединение, но и вычесть из одного множества другое. Результат вычитания… Разностью множеств А и В называется множество, содержащее все элементы,… Х Y = {0, 1, 3, 5} {1, 2, 3, 4} = {0, 5}. Если мы найдем разность множеств Y и Х, то результат будет выглядеть…Дополнение
В случаях, когда одно из множеств является подмножеством другого, А В называют дополнением множества В до множества А, и обозначают символом В'А… Пусть В А. Дополнением множества В до множества А называется множество, содержащее все элементы множества А, которые…Формула Грассмана
Теория множеств используется при решении задач следующего вида: В группе зверей 15 умных, 13 – красивых, и 8 мартышек. Сколько зверей в… Решение:Л.Э. Гуревич, Э.Б. Глинер
Введение
Слово «логика» всем хорошо знакомо. Его часто можно встретить на страницах всевозможных печатных изданий, услышать в разговорной речи. Что же означает это слово? Заглянем в толковый словарь С.И. Ожегова. Там сказано: «Логика – наука о законах мышления и его формах» и еще – «Логика – ход рассуждений». Если второе толкование смысла слова «логика» более или менее понятно каждому, то в связи с первым сразу возникает вопрос: а что такое формы и законы мышления?
Подобно Журдену из пьесы Мольера «Мещанин во дворянстве», который очень обрадовался, узнав, что всю жизнь говорит прозой, вам будет приятно узнать, что в большинстве случаев вы мыслите и говорите по законам логики.
Слово «логика» происходит от греческого logos, что, с одной стороны, означает «слово», а с другой – «мысль, рассуждение». Логика изучает акты мышления, зафиксированные в языке в виде слов, предложений и их совокупностей. Таким образом, логика имеет непосредственное отношение к языку, речи, т.е. соприкасается с грамматикой и, более широко, с лингвистикой (наукой о языке). С помощью логических средств наш естественный язык уточняется, приобретает четкость и определенность. Как справедливо заметил польский логик А.Тарский, – логика создает возможность лучшего взаимопонимания между теми, кто к этому стремится.
Многим хорошо известно, что логика – неотъемлемая составная часть математики. Без логики в математике – ни шагу: ни тебе теорему доказать, ни формулу вывести, ни задачу решить. Ироническая фраза: «Нематематики считают, что математики считают» намекает на то, что основное занятие математиков – вовсе не счет (как многие полагают), а логические или, иначе говоря, дедуктивные рассуждения – выводы, доказательства. (Слово дедукция происходит от латинского deduction, что значит – выведение). С помощью логики математики выводят из уже имеющихся в их распоряжении математических фактов новые факты.
В этом и заключаются основное назначение и сила логики: с ее помощью, имея некоторый запас достоверных (истинных) знаний, можно получать новые знания, не прибегая к наблюдению или эксперименту, а лишь размышляя и рассуждая по определенным правилам.
Логика входит в арсенал методов любой науки, является частью ее методологии. Многие естественнонаучные факты были открыты с помощью логики.
Однако в математике логика выступает в наиболее отчетливом, нестертом, незавуалированном виде, а ее «удельный вес» несравненно больше, чем в естественных науках. В математической теории количество предложений, содержащих исходное знание (аксиом), сводится к минимуму; основное же содержание теории заключено в предложениях, полученных в результате логических рассуждений (теоремах). Поэтому математику называют дедуктивной наукой в отличие от естественных наук (физики, химии, биологии), в которых основной, ведущий метод – эксперимент. Впрочем, естественные и даже многие гуманитарные науки по мере своего развития все более активно и плодотворно используют математические и логические методы, а возможность представления содержания какой-либо науки (или ее раздела) в виде аксиоматической теории считается показателем высокой степени развития этой науки. Как полагал великий немецкий философ Эммануил Кант (1724-1804 гг.), – «каждая наука в той или иной мере является наукой, в какой мере содержит математику». Быть может, это сказано слишком сильно, однако, этой фразой емко и выразительно определено значение математики для других наук и ее место среди них. Недаром другой знаменитый ученый, наш соотечественник, физик Лев Ландау (1908-1968 гг.) назвал математику «наукой сверхъестественной».
Итак, логика в большей или меньшей степени используется как один из методов в любой науке. Необходима логика и в повседневной жизни. С ее помощью обеспечивается полноценное (адекватное) общение в мире людей и компьютеров. Логика присутствует или, по крайней мере, должна присутствовать в любом споре, судебном разбирательстве, расследовании преступления (Шерлок Холмс и его дедуктивный метод!).
В высшей степени важна логика в законотворчестве: формулировка закона должна исключать возможность его неоднозначного толкования. «Логика – это необходимый инструмент, освобождающий от лишних, ненужных запоминаний, помогающий найти в массе информации то ценное, что нужно человеку. Без логики – это слепая работа» – так сказал о роли логики в познавательной, в частности в учебной деятельности, академик П. Анохин.
Почему же логика – столь универсальный инструмент, полезный, более того – необходимый в любой интеллектуальной деятельности? Чем объясняется ее общезначимость? Рассмотрим три рассуждения.
1 Все насекомые – шестиногие. У паука – не шесть ног (а восемь!). Следовательно, паук не насекомое.
2 Все числа, кратные 10, оканчиваются нулем. Число п не оканчивается нулем. Следовательно, число п не кратно 10.
3 Все отличники в Петином классе занимаются спортом. Петя не занимается спортом. Следовательно, Петя – не отличник.
Все эти короткие, одношаговые рассуждения (умозаключения) имеют одну и ту же форму: Все А – это В; не В. Следовательно, не А. Умозаключение такой формы всегда приводит к верному (истинному) выводу (заключению, следствию), если исходные утверждения (посылки) истинны. Формы рассуждений, обладающие свойством «перерабатывать» любые истины в новые истины, называются правильными. Логика дает нам свод правильных форм основных, простейших рассуждений (умозаключений) и правила построения из них сколь угодно длинных и сложных дедуктивных рассуждений, которые применимы в любой области знаний. Этим и объясняется универсальность и «вездесущность» логики, ни с чем не сравнимое многообразие сфер ее применения.
Логика, хотя и связана с языком, но, в отличие от лингвистики, изучает не формы языка, а отраженные в языке формы мышления. А, как известно, несмотря на все различия языков, человечество имеет общее достояние в виде некоторой совокупности мыслей. Идея универсальности логики была использована при создании линкоса, языка для связи с инопланетными цивилизациями. При этом предполагалось, что логические формы и законы, свойственные человеческому мышлению, присущи всякому разуму, и что поэтому такой «логический» язык вместе с языком математических абстракций может стать средством общения в самом широком смысле и масштабе.
Логика как наука сформировалась очень давно – в IV в. до н.э. Ее создал древнегреческий ученый Аристотель. В течение многих веков логика сколько-нибудь существенно не развивалась. Это, конечно, свидетельствует о гениальности Аристотеля, которому удалось создать столь полную научную систему, что, казалось, «не убавить, не прибавить». Однако в силу такой неизменности логика приобрела славу мертвой, застывшей науки и вызывала у многих скептическое к себе отношение. Сухость и кажущуюся закостенелость, бесплодность логики высмеяли в своих бессмертных произведениях Ф. Рабле и Д. Свифт («Гаргантюа и Пантагрюэль» и «Путешествие Гулливера»). В XVII в. великий немецкий ученый Готфрид Лейбниц (1646-1716) задумал создать новую логику, которая была бы «искусством исчисления». В этой логике, по мысли Лейбница, каждому понятию соответствовал бы символ, а рассуждения имели бы вид вычислений. Эта идея Лейбница, не встретив понимания современников, не получила в то время распространения и развития.
Только в середине XIX в. ирландский математик и логик Джордж Буль (1815-1864) частично воплотил в жизнь идею Лейбница. Им была создана алгебра логики, в которой действуют законы, схожие с законами обычной алгебры, но буквами обозначаются не числа, а предложения. На языке булевой алгебры можно описывать рассуждения и «вычислять» их результаты; однако, ею охватываются далеко не всякие рассуждения, а лишь определенный тип их, в некотором смысле – простейший.
Алгебра логики Буля явилась зародышем новой науки – математической логики. В отличие от нее логику, восходящую к Аристотелю, называют традиционной или классической формальной логикой. Таким образом, математическая логика – это логика, использующая язык и методы математики.
Математическая логика сама стала областью математики, поначалу казавшейся в высшей степени абстрактной и бесконечно далекой от практических приложений. Сегодня математическая логика используется в биологии, медицине, лингвистике, педагогике, психологии, экономике, технике. Велика роль математической логики в развитии вычислительной техники: она используется в конструировании компьютеров и при разработке искусственных языков для общения с ними.
Высказывания и операции над высказываниями
Высказывание – это повествовательное предложение (утверждение), о котором можно говорить, что оно истинно или ложно.
Высказывания обозначают большими или маленькими латинскими буквами.
Пример 1. А: «Москва – столица России» – истинное высказывание. b = «Волга впадает в Черное море» – ложное высказывание.
Значения истинности высказываний обозначаются буквами И – «истина» и Л – «ложь» или цифрами 1 – «истина» и 0– «ложь». Т.е. А = 1(И), b = 0(Л).
Не всякое предложение является высказыванием. Так, к высказываниям не относятся вопросительные, и восклицательные предложения, поскольку говорить об их истинности или ложности нет смысла. Не являются высказываниями и такие предложения: «Каша – вкусное блюдо», «Математика – интересный предмет». Нет, и не может быть единого мнения о том, истинны эти предложения или ложны. Предложение «Существуют инопланетные цивилизации» следует считать высказыванием, так как объективно оно либо истинное, либо ложное, хотя пока никто не знает, какое именно.
Предложения «Шел снег», «Площадь комнаты равна 20 м2», «а2 = 4» не являются высказываниями; для того, чтобы имело смысл говорить об их истинности или ложности, нужны дополнительные сведения: когда шел снег, о какой конкретно комнате идет речь, какое число обозначено буквой а. В последнем примере а может не обозначать конкретного числа, а быть переменной, т.е. буквой, вместо которой можно подставлять элементы некоторого множества, называемые значениями переменной. Пусть, например, {-2; 0; 2; 3; 4} – множество значений переменной а. Каждому значению переменной соответствует либо истинное, либо ложное высказывание. Например: высказывания «(-2)2 = 4» и «22 = 4» истинны, а высказывания «02 = 4», «32 = 4» и «42 = 4» ложны.
Предложение, которое содержит хотя бы одну переменную и становится высказыванием при подстановке вместо всех переменных их значений, называется высказывательной формой.
Рассмотрим предложения: «Он рыжеволос» и «Число делится на 7». Эти предложения не содержат переменных в явном виде, но, тем не менее, являются высказывательными формами: первое из них становится высказыванием (истинным или ложным) только после замены местоимения «он» именем конкретного человека из некоторого множества людей мужского пола; второе становится высказыванием, если вместо слова «число» подставлять целые числа. Иначе эти предложения можно записать так: «Человек х рыжеволос», «Число у делится на 7».
Из высказывательных форм можно получать высказывания также с помощью специальных слов, так называемых кванторов. Их два: 1) квантор всеобщности – 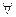 (любой, всякий, каждый); 2) квантор существования –
(любой, всякий, каждый); 2) квантор существования – 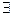 (существует, найдется, имеется, некоторый, по меньшей мере, один). Например, из высказывательной формы «Площадь комнаты 20 м2» можно с помощью кванторов получить высказывания: «Площадь любой комнаты 20 м2» – ложное, «Существует комната, площадь которой 20 м2» – истинное.
(существует, найдется, имеется, некоторый, по меньшей мере, один). Например, из высказывательной формы «Площадь комнаты 20 м2» можно с помощью кванторов получить высказывания: «Площадь любой комнаты 20 м2» – ложное, «Существует комната, площадь которой 20 м2» – истинное.
Из двух данных предложений можно образовывать новые предложения с помощью союзов «и», «или», «либо», «если…, то…», «…тогда и только тогда, когда…» и других. С помощью частицы «не» и словосочетания «неверно, что…» из одного предложения можно получить новое. Наиболее употребительными являются союзы «и», «или», «если…, то…» и «…тогда и только тогда, когда». Остальные союзы считают близкими по смыслу одному из перечисленных союзов.
Союзы «и», «или», «если, то», «тогда и только тогда, когда», а также частицу «не» (словосочетание «неверно, что») называют логическими связками.
Предложения, образованные из других предложений с помощью логических связок, называют составными или сложными. Предложения, которые не содержат логических связок, называют элементарными или простыми.
Пример 2. Из предложений «Солнце всходит на востоке» и «Солнце заходит на западе» можно получить следующие составные высказывания: «Солнце всходит на востоке и заходит на западе»; «Солнце всходит на востоке или заходит на западе»; «Если солнце всходит на востоке, то оно заходит на западе»; «Солнце всходит на востоке тогда и только тогда, когда оно заходит на западе»; «Солнце не всходит на востоке» или «Неверно, что солнце заходит на западе».
В грамматике различают предложения простые и сложные. Предложение, простое по своей грамматической структуре, может быть составным с точки зрения логики. Например, простое с точки зрения грамматики предложение «На улице холодно и сыро» считается в логике сложным, так как образовано с помощью логической связки «и» из двух элементарных предложений «На улице холодно» и «На улице сыро». Простое предложение «Завтра не будет осадков» по своей логической структуре не является элементарным, так как содержит логическую связку «не».
Возникает вопрос: как определить значение истинности сложного высказывания?
В математической логике смысл логических связок уточняется так, чтобы вопрос об истинности или ложности составных предложений, образованных из высказываний во всех случаях решался однозначно. Таким уточнением займемся ниже.
Процесс получения составных высказываний с помощью логических связок называется логической операцией.
По числу логических связок выделяют пять логических операций.
1 Негация (отрицание) – единственная операция, которая может применяться к одному высказыванию.
Негацией высказывания называется новое высказывание, которое истинно тогда и только тогда, когда само высказывание ложно и ложно, когда само высказывание истинно.
Негация обозначается 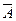 , или ¬b, читается: «не А» или «неверно, что А».
, или ¬b, читается: «не А» или «неверно, что А».
Например, высказывание А = «Луна – спутник Марса» – ложное, а высказывание 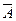 = «Неверно, что Луна – спутник Марса» – истинное.
= «Неверно, что Луна – спутник Марса» – истинное.
Для произвольного высказывания А определение удобно записывать с помощью так называемой таблицы истинности:
| А | 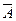
|
Пример 3. Сформулировать отрицание высказываний: А = «Курган – большой город»; В = «Сыр делают из молока»; С = «32 не делится на 4»; D = «Все дети любят манную кашу».
Решение. 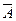 = «Неверно, что Курган – большой город»;
= «Неверно, что Курган – большой город»;  = «Сыр делают не из молока»;
= «Сыр делают не из молока»;  = «32 делится на 4».
= «32 делится на 4».
2Конъюнкция (логическое умножение) – от латинского conjunctio – соединение.
Конъюнкцией двух высказываний называется новое высказывание, которое истинно тогда и только тогда, когда оба высказывания истинны.
Таблица истинности для конъюнкции выглядит следующим образом: А В … Пример 4.Определить значение истинности высказываний «Париж расположен на Сене… Решение. Первое высказывание является конъюнкцией двух высказываний А = «Париж расположен на Сене» и В = «2 + 3 = 5».…Дизъюнкцией двух высказываний является новое высказывание, которое ложно тогда и только тогда, когда оба высказывания ложны.
Таблица истинности для дизъюнкции выглядит следующим образом: А В … Пример 5.Определить значение истинности высказываний «Париж расположен на Сене или 2 + 3 = 5»; «1 – простое число или…Эквиваленцией двух высказываний называется новое высказывание, которое истинно тогда и только тогда, когда оба высказывания одновременно истинны либо ложны.
Эквиваленция обозначается 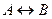 или
или 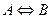 , читается «А тогда и только тогда, когдаВ».
, читается «А тогда и только тогда, когдаВ».
Таблица истинности для эквиваленции выглядит так:
| А | В | 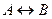
|
В форме эквиваленции, как правило, формулируются определения (например, определения логических операций).
Пример 7.Пусть через А обозначено высказывание «9 делится на 3», а через В – высказывание «10 делится на 3». Составьте высказывания, имеющие логическую структуру: а)  ; б)
; б) 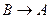 ; в)
; в) 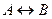 ; г)
; г) 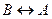 ; д)
; д) 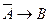 ; е)
; е) 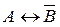 и определите их значения истинности.
и определите их значения истинности.
Решение. а)  = «Если 9 делится на 3, то 10 делится на 3» = 0, т.к. А = 1, а В = 0. б)
= «Если 9 делится на 3, то 10 делится на 3» = 0, т.к. А = 1, а В = 0. б) 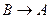 = «Если 10 делится на 3, то 9 делится на 3» = 1. в)
= «Если 10 делится на 3, то 9 делится на 3» = 1. в) 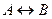 = «9 делится на 3 тогда и только тогда, когда 10 делится на 3» = 0. г)
= «9 делится на 3 тогда и только тогда, когда 10 делится на 3» = 0. г) 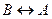 = «10 делится на 3 тогда и только тогда, когда 9 делится на 3» = 0. д)
= «10 делится на 3 тогда и только тогда, когда 9 делится на 3» = 0. д) 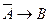 = «Если 9 не делится на 3, то 10 делится на 3» = 1 (т.к. А = 1, то
= «Если 9 не делится на 3, то 10 делится на 3» = 1 (т.к. А = 1, то 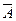 = 0 и В = 0, следовательно,
= 0 и В = 0, следовательно, 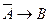 = 1). е)
= 1). е) 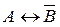 = «9 делится на 3 тогда и только тогда, когда 10 не делится на 3» = 1 (А = 1 и
= «9 делится на 3 тогда и только тогда, когда 10 не делится на 3» = 1 (А = 1 и  = 1, тогда
= 1, тогда 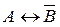 = 1).
= 1).
Формулы логики высказываний
В логике высказываний – первом и основном разделе математической логики – элементарные высказывания рассматриваются как нерасчленяемые «атомы», а… Так как смысл высказываний математическую логику не интересует, их вполне… Пусть X, Y,…, Z,…, Xi, Yi,…, Zi – переменные, вместо которых можно подставить любые элементарные высказывания (или их…Никаких других формул в логике высказываний нет.
Условимся для упрощения записей не заключать в скобки формулы, не являющиеся частями других формул или стоящие под знаком отрицания. Заметим, что в… Опишем процедуру формализации высказываний: 1 Если высказывание – простое, то ему ставится в соответствие элементарная формула.Введение
Представителям самых различных специальностей приходится решать задачи, в которых рассматриваются те или иные комбинации, составленные из букв, цифр и иных объектов. Начальнику цеха надо распределить несколько видов работ между имеющимися станками, агроному – разместить посевы сельскохозяйственных культур на нескольких полях, заведующему учебной частью школы – составить расписание уроков, ученому-химику – рассмотреть возможные связи между атомами и молекулами, лингвисту – учесть различные варианты значений букв незнакомого языка и т.д. Область математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов, называется комбинаторикой.
Комбинаторика как наука возникла в XVI веке. В жизни тогдашнего общества большое место занимали азартные игры. В карты и кости выигрывались и проигрывались золото и бриллианты, дворцы и имения, породистые кони и дорогие украшения. Широко были распространены всевозможные лотереи. Понятно, что первоначально комбинаторные задачи касались в основном азартных игр – вопросов, сколькими способами можно выбросить данное число очков, бросая две или три кости, или сколькими способами можно получить двух королей в данной карточной игре. Эти и другие проблемы азартных игр явились движущейся силой в развитии комбинаторики и развивавшейся одновременно с ней теории вероятностей.
Одним из первых занялся подсчетом числа различных комбинаций при игре в кости итальянский математик Н. Тарталья. Он составил таблицу, показывающую, сколькими способами могут выпасть r костей. Однако при этом не учитывалось, что одна и та же сумма очков может быть получена разными способами (например, 1 + 3 + 4 = 4 + 2 + 2).
Теоретическое исследование вопросов комбинаторики предприняли в XVII веке французские ученые Б. Паскаль и П. Ферма. Исходным пунктом их исследований тоже были проблемы азартных игр. Особенно большую роль сыграла здесь задача о разделе ставки, которую предложил Паскалю его друг шевалье де Мере, страстный игрок. Проблема состояла в следующем: «матч» в орлянку ведется до шести выигранных партий; он был прерван, когда один игрок выиграл 5 партий, а второй – 4; как разделить ставку? Было ясно, что раздел в отношении 5:4 несправедлив. Применив методы комбинаторики, Паскаль решил задачу в общем случае, когда одному игроку остается до выигрыша r партий, а второму s партий. Другое решение дал Ферма.
Дальнейшее развитие комбинаторики связано с именами Я. Бернулли, Г.Лейбница и Л. Эйлера. Однако и у них основную роль играли приложения к различным играм (лото, солитер и др.). За последние годы комбинаторика переживает период бурного развития, связанного с общим повышением интереса к проблемам дискретной математики. Комбинаторные методы используются при решении транспортных задач, в частности задач по составлению расписаний; для составления планов производства и реализации продукции. Установлены связи между комбинаторикой и задачами линейного программирования, статистики и т.д. Комбинаторика используется для составления и декодирования шифров и для решения других проблем теории информации.
Простейшие комбинаторные задачи
Знакомство с новыми понятиями начнем с двух простых задач. Пример 1. Сколько четных двузначных чисел можно составить из цифр 0, 1, 2, 4,… Решение. Составим таблицу: слева от первого столбца поместим первые цифры искомых чисел, а выше первой строки – вторые…Правила умножения и сложения
Правило умножения для двух независимых испытаний удобно объяснять, используя прямоугольники, разбитые на квадратики, или прямоугольные таблицы. Но… Оказывается, правило умножения для трех, четырех и т. д. испытаний можно… Пример 3. Несколько стран в качестве символа своего государства решили использовать флаг в виде трех горизонтальных…Выбор нескольких элементов. Размещения. Сочетания
В предыдущем параграфе все примеры и упражнения сводились к выбору одного элемента из данного множества и подсчету количества таких выборов. А если… Пример 10. В чемпионате участвовали 7 команд. Каждая команда играла один матч… Решение. Рассмотрим таблицу результатов встреч размером 7x7 (рис. 4.4).В. Незвал
Введение
Все мы довольно часто говорим «это невероятно», «более вероятно, что...», «это маловероятно», «можно утверждать со стопроцентной вероятностью, что...», когда пытаемся спрогнозировать наступление того или иного события. При этом обычно опираемся на интуицию, жизненный опыт, здравый смысл и т.п. Но очень часто такие приблизительные оценки оказываются недостаточными: бывает важно знать, на сколько или во сколько раз совершение одного случайного события вероятнее другого. Иными словами, нужны точные количественные оценки, надо уметь численно характеризовать возможность наступления того или иного события. Раздел математики, посвященный исследованию количественных оценок случайных событий, называется теорией вероятностей.
Ее основателями считают Пьера Ферма и Блеза Паскаля. Эти французские ученые XVII века первыми нашли ключ к составлению количественной оценки вероятности события. Они использовали метод, который позже был назван комбинаторным анализом, или, проще, комбинаторикой.
Однако мы не будем сейчас говорить ни о предмете, ни о содержании теории вероятностей и комбинаторики, а просто приведем пример, который иллюстрирует все вышесказанные слова.
Начальник написал 10 различных писем и поручил своему помощнику надписать 10 конвертов с нужными адресами. Тот так и сделал, но дальнейшее перепоручил секретарше. Она выполнила это ответственное задание формально, то есть разложила письма по конвертам, не обращая внимания на адреса. Какова вероятность того, что ни одно письмо не попало в нужный конверт? Ответ оказывается на удивление большим: вероятность такой масштабной ошибки превышает 36%!
Случайные события и их вероятности
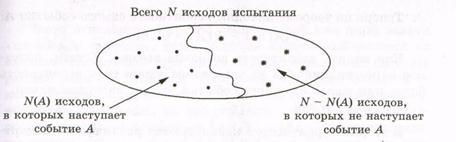
Всякое действие, явление, наблюдение с несколькими различными исходами, реализуемое при данном комплексе условий, будем называть испытанием. Например, многократное подбрасывание монеты, процесс изготовления какой-либо… Результат этого действия или наблюдения будем называть событием.Принять предположение о равновероятности (равновозможности) всех этих исходов;
4) найти частное , оно и будет равно вероятности события А. Принято вероятность события А обозначать: Р(А). Объяснение такого обозначения… Используя это обозначение, вероятность события А по классической схеме можно найти с помощью формулы .КЛАССИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ Вероятностью события А при проведении некоторого испытания называют отношение числа исходов, в результате которых наступает событие А, к общему числу всех равновозможных между собой исходов этого испытания.
Пример 2. Найти вероятность того, что при одном бросании игрального кубика выпадет: а) 4; б) 5; в) четное число очков; г) число очков, большее 4; д) число очков, не кратное трем.
Решение. Всего имеется N = 6 возможных исходов: выпадение грани куба с числом очков, равным 1, 2, 3, 4, 5 или 6. Мы считаем, что ни один из них не имеет никаких преимуществ перед другими, т. е. принимаем предположение о равновероятности этих исходов.
а) Ровно в одном из исходов произойдет интересующее нас событие А – выпадение числа 4. Значит, N(А) = 1 и 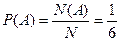 .
.
б) Решение и ответ такие же, как и в предыдущем пункте.
в) Интересующее нас событие В произойдет ровно в трех случаях, когда выпадет число очков 2, 4 или 6. Значит, N(B) = 3 и 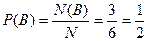 .
.
г) Интересующее нас событие С произойдет ровно в двух случаях, когда выпадет число очков 5 или 6. Значит, N(C) = 2 и 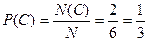 .
.
д) Из шести возможных выпавших чисел четыре (1, 2, 4, и 5) не кратны трем, а остальные два (3 и 6) делятся на три. Значит, интересующее нас событие наступает ровно в четырех из шести возможных и равновероятных между собой исходах опыта. Поэтому в ответе получается 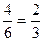 .
.
Ответ: а)  ; б)
; б)  ; в)
; в)  ; г)
; г) 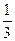 ; д)
; д)  .
.
Реальный игральный кубик вполне может отличаться от идеального (модельного) кубика, поэтому для описания его поведения требуется более точная и детальная модель, учитывающая преимущества одной грани перед другой, возможное наличие магнитов и т. п. Но «дьявол кроется в деталях», а большая точность ведет, как правило, к большей сложности, и получение ответа становится проблемой. Мы же ограничиваемся рассмотрением простейшей вероятностной модели, где все возможные исходы равновероятны.
Замечание 1. Рассмотрим еще пример. Был задан вопрос: «Какова вероятность выпадения тройки при одном бросании кубика?» Ученик ответил так: «Вероятность равна 0,5». И объяснил свой ответ: «Тройка или выпадет, или нет. Значит, всего есть два исхода и ровно в одном наступает интересующее нас событие. По классической вероятностной схеме получаем ответ 0,5». Есть в этом рассуждении ошибка? На первый взгляд – нет. Однако она все же есть, причем в принципиальном моменте. Да, действительно, тройка или выпадет, или нет, т. е. при таком определении исхода бросания N = 2. Правда и то, что N(А) = 1 и уж, разумеется, верно, что  = 0,5, т.е. три пункта вероятностной схемы учтены, а вот выполнение пункта 2) вызывает сомнения. Конечно, с чисто юридической точки зрения, мы имеем право считать, что выпадение тройки равновероятно ее невыпадению. Но вот можем ли мы так считать, не нарушая свои же естественные предположения об «одинаковости» граней? Конечно, нет! Здесь мы имеем дело с правильным рассуждением внутри некоторой модели. Только вот сама эта модель «неправильная», не соответствующая реальному явлению.
= 0,5, т.е. три пункта вероятностной схемы учтены, а вот выполнение пункта 2) вызывает сомнения. Конечно, с чисто юридической точки зрения, мы имеем право считать, что выпадение тройки равновероятно ее невыпадению. Но вот можем ли мы так считать, не нарушая свои же естественные предположения об «одинаковости» граней? Конечно, нет! Здесь мы имеем дело с правильным рассуждением внутри некоторой модели. Только вот сама эта модель «неправильная», не соответствующая реальному явлению.
Замечание 2. Рассуждая о вероятности, не упускайте из виду следующее важное обстоятельство. Если мы говорим, что при бросании кубика вероятность выпадения одного очка равна  , это совсем не значит, что, кинув кубик 6 раз, вы получите одно очко ровно один раз, бросив кубик 12 раз, вы получите одно очко ровно два раза, бросив кубик 18 раз, вы получите одно очко ровно три раза и т. д. Слово вероятно носит предположительный характер. Мы предполагаем, что, скорее всего, может произойти. Вероятно, если мы бросим кубик 600 раз, одно очко выпадет 100 раз или около 100. Если у вас будет время и желание, проведите эксперимент: бросьте игральный кубик, например, 60 раз и составьте таблицу выпадений очков 1, 2, 3, 4, 5, 6. Скорее всего (вероятнее всего), все числа в вашей таблице будут около 10.
, это совсем не значит, что, кинув кубик 6 раз, вы получите одно очко ровно один раз, бросив кубик 12 раз, вы получите одно очко ровно два раза, бросив кубик 18 раз, вы получите одно очко ровно три раза и т. д. Слово вероятно носит предположительный характер. Мы предполагаем, что, скорее всего, может произойти. Вероятно, если мы бросим кубик 600 раз, одно очко выпадет 100 раз или около 100. Если у вас будет время и желание, проведите эксперимент: бросьте игральный кубик, например, 60 раз и составьте таблицу выпадений очков 1, 2, 3, 4, 5, 6. Скорее всего (вероятнее всего), все числа в вашей таблице будут около 10.
Пример 3. Найти вероятность того, что при двукратном бросании игрального кубика произведение выпавших очков будет: а) кратно 5; б) кратно 6.
Решение. При каждом из двух бросаний кубика возможны 6 исходов. Предполагается, что эти два испытания независимы друг от друга. По правилу умножения получаем, что данный опыт имеет 6 • 6 = 36 исходов. Будем действовать по классической вероятностной схеме, т. е. считать, что все N = 36 исходов равновероятны между собой.
Все 36 исходов можно перечислить. Например, с помощью таблицы. В данном случае все исходы – это пары (1; 1), (1; 2), ..., (1; 6), (2; 1), (2; 2), ..., (6; 5), (6; 6).
а) Если на первом месте стоит 5, то при любой второй цифре их произведение кратно 5. Получается шесть вариантов: (5; 1), (5; 2), (5; 3), (5; 4), (5; 5), (5; 6). Еще шесть вариантов получается, если 5 стоит на втором месте. Так как 5 – простое число, то других вариантов нет.
Вроде бы, ответ 6 + 6 = 12. Но один результат (5; 5) мы посчитали дважды. Значит, интересующее нас событие А наступает ровно в 11 из возможных 36 равновероятных между собой исходах, т. е. N(А) = 11, поэтому  .
.
б) Если на первом или на втором месте стоит 6, то произведение выпавших чисел делится на 6, а всего таких вариантов, как и в случае а), будет 11. Но произведение выпавших чисел будет кратно 6 в тех случаях, когда одно из чисел, отличных от 6, - четное, а другое кратно 3. Перечислим благоприятные варианты: (2; 3), (4; 3), (3; 2), (3; 4) – всего 4 варианта. Добавив их к указанным выше 11 вариантам, получим 15 благоприятных исходов, т.е. N(А) = 15. Значит,  .
.
Ответ: а) 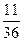 , б)
, б) 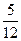 .
.
Задачи на отыскание вероятностей случайных событий «в два с половиной раза» сложнее задач по комбинаторике. Сначала мы используем комбинаторику при нахождении N – количества всех исходов опыта. Во второй раз комбинаторика нужна при нахождении N(А). При этом во второй раз – это уже более сложная комбинаторика. Наконец, надо еще уметь вычислить значение дроби. Вот и получается «две с половиной комбинаторики».
Теория вероятностей возникла в XVII веке при анализе различных азартных игр. Неудивительно поэтому, что первые примеры носят игровой характер. От примеров с игральными кубиками перейдем к случайному вытаскиванию игральных карт из колоды.
Пример 4. Из колоды в 36 карт случайным образом одновременно вытаскивают 3 карты. Какова вероятность того, что среди них нет пиковой дамы?
Решение. У нас имеется множество из 36 элементов. Мы производим выбор трех элементов, порядок которых не важен. Значит, возможно получение N = 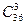 исходов. Будем действовать по классической вероятностной схеме, т. е. предположим, что все эти исходы равновероятны.
исходов. Будем действовать по классической вероятностной схеме, т. е. предположим, что все эти исходы равновероятны.
Среди всех N =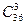 исходов нам следует сосчитать те, в которых нет пиковой дамы (событие А). Отложим даму пик в сторону, и из оставшихся 35 карт будем выбирать 3 карты. Получатся все интересующие нас варианты. Значит, N(А) =
исходов нам следует сосчитать те, в которых нет пиковой дамы (событие А). Отложим даму пик в сторону, и из оставшихся 35 карт будем выбирать 3 карты. Получатся все интересующие нас варианты. Значит, N(А) = 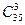 .
.
Осталось вычислить нужную вероятность по классическому определению: 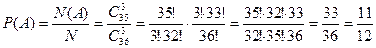 .
.
Операции с вероятностями
А чему равна вероятность того, что среди выбранных трех карт есть пиковая дама? Число всех таких исходов нетрудно посчитать, надо просто из всех исходов N вычесть все те исходы, в которых дамы пик нет, т. е. вычесть найденное в примере 4 число N(А). Затем эту разность N – N(А) в соответствии с классической вероятностной схемой следует поделить на N. Вот что получим: 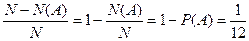 .
.
Мы видим, что между вероятностями двух событий имеется определенная связь. Если событие А заключается в отсутствии дамы пик, а событие В состоит в ее наличии среди выбранных трех карт, то
Р(В) = 1 – Р(А);
Р(А) + Р(В) = 1.
К сожалению, в равенстве Р(А) + Р(В) = 1 нет никакой информации о связи событий А и В между собой; эту связь нам приходится держать в уме. Удобнее было бы заранее дать событию В название и обозначение, явно указывающие на его связь с А.
Определение 1. Событие В называют противоположным событиюА и обозначают В = 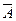 , если событие В происходит тогда и только тогда, когда не происходит событие А.
, если событие В происходит тогда и только тогда, когда не происходит событие А.
Символ 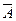 можно читать так: «А с чертой». Иллюстрация этого определения приведена на рисунке 5.1.
можно читать так: «А с чертой». Иллюстрация этого определения приведена на рисунке 5.1.
ТЕОРЕМА 1. Для нахождения вероятности противоположного события следует из единицы вычесть вероятность самого события: Р(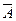 )= 1 - Р(А).
)= 1 - Р(А).
|
Рисунок 5.1
В самом деле, 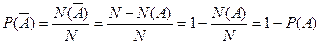
На практике вычисляют то, что проще найти: или Р(А), или Р(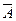 ). После этого пользуются формулой из теоремы и находят, соответственно, или Р(А) = 1 - Р(
). После этого пользуются формулой из теоремы и находят, соответственно, или Р(А) = 1 - Р(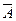 ), или Р(
), или Р(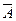 ) = = 1 - Р(А).
) = = 1 - Р(А).
Пример 5.Из колоды в 36 карт случайным образом вытаскивают 5 карт. Какова вероятность того, что среди выбранных карт будет хотя бы одна карта бубновой масти?
Решение. Из множества в 36 элементов мы производим выбор пяти элементов, причем порядок этих элементов не важен. Значит, возможно получение 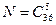 исходов. Будем действовать по классической вероятностной схеме, т. е. предположим, что все эти исходы равновероятны между собой.
исходов. Будем действовать по классической вероятностной схеме, т. е. предположим, что все эти исходы равновероятны между собой.
Если А – интересующее нас событие, то противоположное ему событие 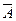 состоит в том, что среди выбранных пяти карт нет ни одной карты бубновой масти. Но это значит, что все 5 карт выбраны из других карточных мастей, т. е. из 36 - 9 = 27 карт. Значит, N(А) =
состоит в том, что среди выбранных пяти карт нет ни одной карты бубновой масти. Но это значит, что все 5 карт выбраны из других карточных мастей, т. е. из 36 - 9 = 27 карт. Значит, N(А) = 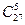 и можно легко найти вероятность события А:
и можно легко найти вероятность события А: 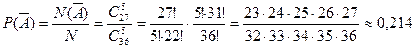 .
.
Теперь по теореме находим вероятность самого события А: Р(А) = 1 - Р(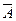 ) ≈ 0,786.
) ≈ 0,786.
Как видим, вероятность довольна высока. Кстати, полезное напоминание: без калькулятора вычислить вероятность более или менее сложного события бывает затруднительно.
Ответ: ≈ 0,786.
В теории вероятностей используются различные стандартные игровые ситуации. Это бросание монеты или игрального кубика, вытаскивание карт из колоды. К этому списку добавим еще одну, назовем ее «урновая схема»: в темном ящике (урне) лежат неотличимые на ощупь шары различного цвета. Один или несколько шаров вытаскивают. Вычисляют вероятность того, что выбранные шары имеют какой-то определенный набор цветов.
Пример 6.В урне лежат 10 белых и 11 рыжих шаров. Случайным образом достают 5 шаров. Какова вероятность того, что среди этих 5 шаров ровно 3 белых?
Решение. Шары в урне предполагаем неразличимыми, из 21 шара случайным образом производят выбор 5 шаров, причем порядок выбора не важен. Значит, существует N = 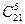 способов такого выбора. Считаем все эти способы равновероятными.
способов такого выбора. Считаем все эти способы равновероятными.
Интересующее нас событие А наступает, когда 3 из 5 шаров – белые, а 2 – рыжие. Из 10 белых шаров, имеющихся в урне, 3 шара можно выбрать 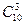 способами, а из 11 рыжих шаров 2 шара –
способами, а из 11 рыжих шаров 2 шара – 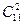 способами. Выбор разноцветных шаров считаем независимым. По правилу умножения получаем, что нужный нам состав шаров можно выбрать N(А) =
способами. Выбор разноцветных шаров считаем независимым. По правилу умножения получаем, что нужный нам состав шаров можно выбрать N(А) = 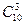 •
• 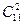 способами. Остается посчитать вероятность.
способами. Остается посчитать вероятность.
 (почти одна треть).
(почти одна треть).
Ответ: ≈ 0,324.
Часто используется способ решения той или иной задачи «перебором случаев», когда условия задачи разбиваются на взаимоисключающие друг друга случаи, каждый из которых рассматривается отдельно. Например, «направо пойдешь – коня потеряешь, прямо пойдешь – задачу по теории вероятности решать будешь, налево пойдешь – ...». Или при построении графика функции у = 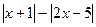 рассматривают случаи х < -1;
рассматривают случаи х < -1;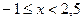 ;
; 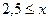 . В каждом из трех случаев «раскрывают» модуль, строят нужные графики линейных функций и затем объединяют соответствующие части этих графиков; фактически речь идет о построении графика кусочной функции. Этот же метод часто используют и при подсчете вероятностей.
. В каждом из трех случаев «раскрывают» модуль, строят нужные графики линейных функций и затем объединяют соответствующие части этих графиков; фактически речь идет о построении графика кусочной функции. Этот же метод часто используют и при подсчете вероятностей.
Пример7. Из 50 точек 17 закрашены в синий цвет, а 13 – в оранжевый цвет. Найти вероятность того, что случайным образом выбранная точка окажется закрашенной.
Решение. Всего закрашено 30 точек из 50. Значит, вероятность равна 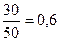
Ответ: 0,6.
Рассмотрим, однако, этот простой пример более внимательно. Пусть событие А состоит в том, что выбранная точка – синяя, а событие В состоит в том, что выбранная точка – оранжевая (рисунок 5.2). По условию, события А и В не могут произойти одновременно.
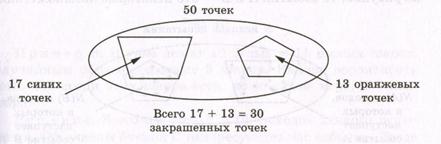 |
Обозначим буквой С интересующее нас событие. Событие С наступает тогда и только тогда, когда происходит хотя бы. одно из событий А или В. Ясно, что N(С) = N(А) + N(В).
Рисунок 5.2
Поделим обе части этого равенства на N – число всехвозможных исходов данного опыта; получим 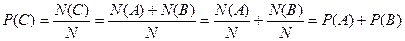 .
.
Мы на простом примере разобрали важную и часто встречающуюся ситуацию. Для нее есть специальное название.
Определение 2. События А и В называют несовместными,если они не могут происходить одновременно. В противном случае события называются совместными.
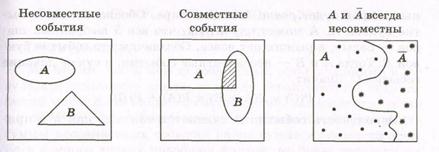
Рисунок 5.3
ТЕОРЕМА 2. Вероятность наступления хотя бы одного из двух несовместных событий равна сумме их вероятностей.
При переводе этой теоремы на математический язык возникает необходимость как-то назвать и обозначить событие, состоящее в наступлении хотя бы одного из двух данных событий А и В. Такое событие называют суммой событий А и В и обозначают А + В.
Если А и В несовместны, то
Р(А + В) = Р(А) + Р(В).
Несовместность событий А и В удобно иллюстрировать следующим рисунком (рисунок 5.4). Если все исходы опыта – некоторое множество точек на рисунке, то события А и В – это некоторые подмножества данного множества. Несовместность А и В означает, что эти два подмножества не пересекаются между собой. Типичный пример несовместных событий – любое событие А и противоположное событие А.
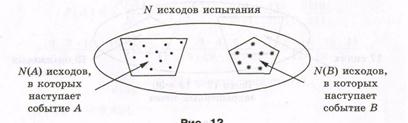
Рисунок 5.4
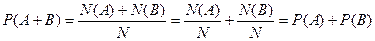
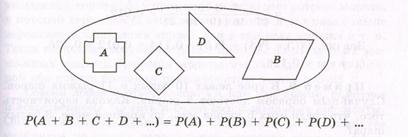 Разумеется, указанная теорема верна и для трех, и для четырех, и для любого конечного числа попарно несовместных событий. Вероятность суммы любого числа попарно несовместных событий равна сумме вероятностей этих событий.
Разумеется, указанная теорема верна и для трех, и для четырех, и для любого конечного числа попарно несовместных событий. Вероятность суммы любого числа попарно несовместных событий равна сумме вероятностей этих событий.
Рисунок 5.5
Это важное утверждение как раз и соответствует способу решения задач «перебором случаев»:
Пример 8. В урне лежат 10 белых и 11 рыжих шаров. Случайным образом достают 5 шаров. Какова вероятность того, что среди этих шаров есть, по крайней мере, 4 белых шара?
Решение. Всего имеется N = 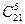 исходов данного испытания. Обозначим буквой С интересующее нас событие. Тогда возможны два случая. Может случиться, что среди 5 выбранных шаров будет ровно 4 белых шара. Обозначим это событие буквой А. А может случиться, что все 5 выбранных шаров – белые, а рыжих нет вовсе. Обозначим это событие буквой В. Тогда А и В – несовместные события, в сумме дающие событие С. Значит, Р(С) = Р(А + В) = Р(А) + Р(В).
исходов данного испытания. Обозначим буквой С интересующее нас событие. Тогда возможны два случая. Может случиться, что среди 5 выбранных шаров будет ровно 4 белых шара. Обозначим это событие буквой А. А может случиться, что все 5 выбранных шаров – белые, а рыжих нет вовсе. Обозначим это событие буквой В. Тогда А и В – несовместные события, в сумме дающие событие С. Значит, Р(С) = Р(А + В) = Р(А) + Р(В).
Вероятность события А считается так же, как и в примере 6:
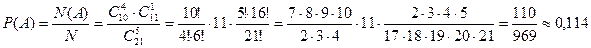 .
.
Так же подсчитывается и вероятность события В.
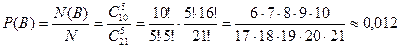
Значит, Р(С) = Р(А) + Р(В) = 0,114 + 0,012 = 0,126.
Ответ: ≈ 0,126.
Пример 9.В урне лежат 10 белых и 11 рыжих шаров. Случайным образом достают 5 шаров. Какова вероятность того, что среди этих 5 шаров есть, по крайней мере, 3 белых шара?
Решение. Пусть А – событие, состоящее в том, что среди выбранных пяти шаров есть роено 3 белых шара, В – событие, состоящее в том, что белых шаров роено 4, и С – событие, означающее, что все 5 выбранных шаров – белые. Тогда события А, В, С попарно несовместны, а нам требуется найти вероятность того, что произойдет или событие А, или событие В, или событие С. Вероятности каждого из этих событий в отдельности нами уже найдены (примеры 6 и 8). Значит, по теореме 2, Р(А + В + С) = Р(А) + Р(В) + Р(С) = 0,324 + 0,114 +…+ 0,012 = 0,45.
Ответ: = 0,45.
Мы видим, что и между событиями, происходящими в результате некоторого опыта, и между вероятностями этих событий могут быть какие-то соотношения, зависимости, связи и т. п. Например, события можно «складывать», а вероятность суммы несовместных событий равна сумме их вероятностей.
Произведением конечного числа событий называется событие, состоящее в том, что каждое из них произойдет.
Вероятность суммы двух совместных событий равна сумме вероятностей этих событий минус вероятность произведения этих событий.
Пусть А и В – два случайных события одного и того же испытания. Тогда условной вероятностью события А или вероятностью события А при условии, что… Из этого определения следует, что Р(АВ)=Р(В)Р(А/В), т.е. вероятность… Пример 10. Из колоды в 36 карт поочередно достают две карты. Найти вероятность того, что вторым вынут червовый король,…Р. фон Мизес
Дни отмерены нам статистиками…
С. Е. Лец
Математическая статистика – это раздел математики, посвященный математическим методам систематизации, обработки и использования статистических данных. Такие данные приносит учет всякого рода массовых явлений и процессов.
Случайные величины
Случайная величина – переменная величина, конкретное значение которой зависит от случая. Например, температура воздуха в 12 ч дня 1 июля в г.… Для характеристики случайной величины необходимо знать множество возможных… Различают случайные величины дискретные и непрерывные. Если множество возможных значений случайной величины конечно…Основные понятия математической статистики
Термин «статистика» в настоящее время употребляется в разных значениях, однако зачастую под ним понимают науку, изучающую массовые явления для выявления закономерностей и получения некоторых обобщенных показателей, кратко характеризующих полученные данные. Как правило, статистика имеет дело с числовыми значениями, которые определяются влиянием множества различных причин, одни из которых – существенные, а другие – случайные. Основная задача статистики состоит в абстрагировании от случайного и выявлении типичного, характерного и закономерного.
Сам термин «статистика» произошел от латинского слова status, что означает «политическое состояние» и первоначально статистикой называли изучение государственных дел, а видных политических деятелей, хорошо осведомленных и потому способных делать обоснованные политические выводы, – statists. Позднее под словом «статистика» стали подразумевать числовые данные, на основе которых государственные деятели делали выводы, а еще позже стали применять и для числовых данных вообще и постепенно пришли к современному значению.
Без статистики невозможно изучать явления и процессы, происходящие в производстве, экономике и т.д. Статистическое изучение тех или иных явлений предполагает в качестве первого шага сбор сведений – статистическое наблюдение. В результате такого наблюдения получается беспорядочная груда сырого материала, нуждающегося в систематизации и обработке.
В основе научной статистики лежит метод группировок. Группировкой называется расчленение совокупности сведений по какому-либо признаку. Благодаря группировкам материал наблюдений принимает упорядоченный (систематизированный) вид. Группировочные признаки могут иметь количественное выражение – заработная плата, успеваемость и т.д. – или качественное – пол, должность, семейное положение и т.п.
Следующий этап обработки собранных данных – вычисление обобщающих показателей. В качестве таких показателей широко известны средние величины. Необходимость вычисления средних величин всегда возникает при изучении массовых явлений. Роль средних величин велика, так как в каждом явлении имеет место сочетание случайности и закономерности. При вычислении средних в силу действия закона больших чисел случайности взаимопоглощаются и уравновешиваются, поэтому появляется возможность переходить от единичного к общему, от случайного – к закономерному.
Характеристики и параметры статистической совокупности
В результате непосредственных наблюдений, измерений или регистрации фактов получается множество данных, которые образуют статистическую совокупность… Основным этапом обработки экспериментальных данных является группировка, т. е.… Сведения, собранные за какой-то период, могут быть систематизированы по времени. Получаемые при этом данные называются…Группировка информации в виде таблиц
Знакомство с элементами статистики начнем с конкретного примера. В девятых классах «А» и «Б» измерили рост 50 учеников. Получились следующие… 162, 168, 157, 176, 185, 160, 162, 158, 181, 179,Графическое представление информации
Итак, выборки удобно задавать с помощью таблиц. Но мы знаем, что и для функций есть табличный способ их задания. Таблицы образуют «мостик», по… Отложим по оси абсцисс значения из первой строки таблицы распределения, а по… Пример 3. Постройте график распределения и многоугольник частот для следующих результатов письменного экзамена по…Гистограммы распределения большого объема информации
Гистограммы особенно незаменимы в случаях, когда ряд данных состоит из очень большого количества чисел (сотни, тысячи и т. п.). В этих случаях… Если ширина столбцов гистограммы достаточно мала, а основания столбцов в… Рисунок 6.7Сложить все результаты, входящие в эту выборку;
Полученную сумму разделить на количество всех результатов.
Например, пусть 10 студентов получили за тест по комбинаторике баллы
9, 14, 12, 9, 15, 12, 9, 15, 12, 12
из двадцати максимально возможных. Тогда среднее значение этой выборки результатов теста равно
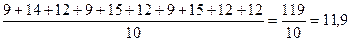
Среднее значение выборки, к сожалению, не имеет наглядной иллюстрации с помощью полигона частот. Оно, по определению, усредняет все различные результаты, заменяя полную, но объемную информацию одним-единственным числом. Само это число, как мы видим, может и не входить в результаты выборки.
Среднее значение выборки можно вычислить, предварительно сгруппировав одинаковые слагаемые в числителе. Смотрите,
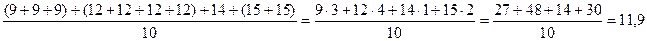 Такой способ подсчета очень удобно применять, когда выборка задана своей таблицей распределения вариант. В нашем примере вариант всего четыре штуки: 9, 12, 14, 15, а их кратности равны, соответственно, 3, 4, 1, 2. Значит, таблица распределения имеет такой вид:
Такой способ подсчета очень удобно применять, когда выборка задана своей таблицей распределения вариант. В нашем примере вариант всего четыре штуки: 9, 12, 14, 15, а их кратности равны, соответственно, 3, 4, 1, 2. Значит, таблица распределения имеет такой вид:
| Варианта | ||||
| Кратность варианты |
Поэтому можно было бы действовать и так. Сначала перемножить числа в каждом столбце этой таблицы. Потом сложить полученные произведения и затем найденную сумму разделить на 10. Сформулируем общее правило.
Для нахождения среднего значения выборки можно:
Каждую варианту умножить на ее кратность;
Сложить все полученные произведения;
Поделить найденную сумму на сумму всех кратностей.
Заметим, что 0,3 – это частота варианты 9; 0,4 – частота варианты 12; 0,1 –… Значит, можно было бы просто перемножить числа в каждом столбце и затем сложить все полученные произведения.…Каждую варианту умножить на ее частоту;
Сложить все полученные произведения.
Приведем еще один пример. Пример 5. Найти размах, моду и математическое ожидание выборки: 4, 6, 3, 8, 4, 3, 5, 4, 5, 6, 4, 3, 6, 5, 4, 3, 5, 7, 8, 4.Экспериментальные данные и вероятности событий
В конце темы рассмотрим связь между вероятностями случайных событий и экспериментальными статистическими данными. А сделаем это на примере бросания… О, О, Р, О, Р, Р, О, Р, Р, Р, О, О, Р, О, Р, О, О, Р, Р, О, О, Р... Иными словами, имеется выборка, в которой две варианты О и Р. Для каждого числа п бросаний монеты можно сосчитать…Р. Шеннон
Под моделью (от лат. modulus – мера, образец, норма) понимают такой материальный или мысленно представляемый объект, который в процессе познания (изучения) замещает объект-оригинал, сохраняя некоторые важные для данного исследования типичные черты. Процесс построения и использования модели называется моделированием.
Два подхода к построению моделей
Способов построения моделей существует великое множество, ибо, пытаясь разобраться в сложившемся положении вещей, можно совершенно по-разному… Правда, не стоит забывать, что нередко упрощенческие подходы к сложным… Можно выделить два подхода к построению моделей (моделированию) тех или иных явлений, событий, обстоятельств, называя…Три типа моделей
Различают три типа моделей – физические, аналоговые и математические модели. Физические модели. Так называют увеличенное или уменьшенное описание объекта… Применяются физические модели в машиностроении, самолетостроении, архитектуре и т.д.Основные этапы математического моделирования
1 Построение модели. На этом этапе задается некоторый «нематематический» объект – явление природы, конструкция, экономический план,… 2 Решение математической задачи, к которой приводит модель. На этом этапе… 3 Интерпретация полученных следствий из математической модели. Следствия, выведенные из модели на языке математики,…Классификация моделей
Классифицировать модели можно по разным критериям. Например, по характеру решаемых проблем модели могут быть разделены на функциональные и структурные. В первом случае все величины, характеризующие явление или объект, выражаются количественно. При этом одни из них рассматриваются как независимые переменные, а другие – как функции от этих величин. Математическая модель обычно представляет собой систему уравнений разного типа (дифференциальных, алгебраических и т.д.), устанавливающих количественные зависимости между рассматриваемыми величинами. Во втором случае модель характеризует структуру сложного объекта, состоящего из отдельных частей, между которыми существуют определенные связи. Как правило, эти связи не поддаются количественному измерению. Для построения таких моделей удобно использовать теорию графов. Граф – это математический объект, представляющий собой некоторое множество точек (вершин) на плоскости или в пространстве, некоторые из которых соединены линиями (ребрами).
По характеру исходных данных и результатов предсказания модели могут быть разделены на детерминистические и вероятностно-статистические. Модели первого типа дают определенные, однозначные предсказания. Модели второго типа основаны на статистической информации, а предсказания, полученные с их помощью, имеют вероятностный характер.
Примеры математических моделей
Задача о движении снаряда.
Снаряд пущен с Земли с начальной скоростью v0 = 30 м/c под углом α = 450 к ее поверхности; требуется найти траекторию его движения и расстояние… 1. Построение модели.Пренебрегая размерами снаряда, будем считать его… Тогда, как это известно из школьного курса физики, движение снаряда описывается формулами:Задача о баке с наименьшей площадью поверхности.
1. Построение модели.Запишем следующие формулы для объема и площади поверхности цилиндра высоты h и радиуса r: , . Выражая h через r и V из первой формулы и подставляя полученное выражение во вторую, получим:Транспортная задача.
Обозначим через aij стоимость перевозки 1 т муки с i-того склада на j-тый завод (i,j = 1,2). Пусть а11 = 1,2 р., а12 = 1,6 р., а21 = 0,8 р., а22 = 1… Как нужно спланировать перевозки, чтобы их стоимость была минимальной? 1. Построение модели.Придадим задаче математическую формулировку. Обозначим через х11 и х12 количество муки, которое…Задача о радиоактивном распаде.
В школьном курсе математического анализа показано, что решение этого дифференциального уравнения имеет вид N(t) = N(0)е-lt. Время Т, за которое…Задача о коммивояжере.
Надо определить порядок посещения городов, при котором длина соответствующего пути минимальна.Построение модели.
Рисунок 7.2 2. Решение математической задачи, к которой приводит модель.Найдем перебором… Заметим, что если в графе п вершин и все вершины попарно соединены между собой ребрами (такой граф называется полным),…Задача о нахождении связи между структурой и свойствами веществ.
Требуется найти приближенную зависимость между температурой кипения и числом п для этих соединений. Рисунок 7.3 1. Построение модели. Предположим, что эта зависимость имеет вид , где а и b – константы, подлежащие определению. Для…Задача об определении надежности электрической цепи.
Предположим, что в электрическую цепь последовательно включены три элемента, работающие независимо друг от друга. Вероятности отказов 1-го, 2-го и… 1. Построение модели. Так как элементы включены последовательно, то тока в… Пусть А – событие, состоящее в том, что тока в цепи не будет; событие Аi (i = 1, 2, 3) заключается в том, что i-тый…Задача о диете.
Дневное питание этими новинками должно давать не более 14 единиц жира (чтобы похудеть), но и не менее 300 калорий (чтобы не сойти с дистанции… Так как дама просто приятная в это время была несколько стеснена в средствах,… 1. Построение модели. Обозначим через х количество продукта Р, а через у – количество продукта Q, требуемые для…Выводы
Модель – это условный образ объекта, построенный для упрощения его исследования.
Конечно, при попытке упрощенного описания ситуации некоторыми обстоятельствами приходится пренебрегать, считая их несущественными. Однако единого взгляда на то, что именно существенно, а что не очень, по-видимому, нет. Можно, например, не обращать внимания на то, что начался дождик. Но одно дело пробежать под накрапывающим дождем сотню метров, и совсем другое – часовая прогулка под таким дождем без зонта.
Предлагая построенную или выбранную нами модель, мы непременно должны указывать пределы, в которых ею можно пользоваться, и предупреждать о том, что нарушение этих ограничений приводит (и, скорее всего, приведет) к серьезным ошибкам. Коротко говоря, у каждой модели есть свой ресурс.
Покупая блузку или рубашку, мы привыкли к наличию меток, на которых указаны максимально допустимая температура глажения, дозволенные виды стирки и т.п. Это, конечно, ни в коей мере не означает, что нам запрещается, взяв докрасна раскаленный утюг, пройтись им по ткани раз-другой. Такое мы сделать можем. Но вот захотим ли мы носить блузку или рубашку после такого глажения?
Таким образом, построение модели опирается на значительное упрощение изучаемой ситуации и, следовательно, к получаемым на ее основе выводам нужно относиться достаточно осторожно – модель может не все.
Вместе с тем, даже весьма грубая на вид идеализация нередко позволяет глубже вникнуть в суть проблемы. Пробуя как-то влиять на параметры модели (выбирать их, управлять ими), мы получаем возможность подвергнуть исследуемое явление качественному анализу и сделать выводы общего характера.
Контрольные вопросы
1 Что такое модель, моделирование?
2 Какие два подхода различают в моделировании? В чем их особенность?
3 Перечислите типы моделей. Дайте им краткую характеристику.
4 В чем важность математического моделирования?
5 Перечислите этапы математического моделирования. Охарактеризуйте каждый этап.
6 Как можно классифицировать математические модели?
7 Приведите пример задачи математического моделирования.
8 Почему нужно с осторожностью относиться к выводам, полученным на основе модели?
Тема 8: Элементы истории математики
После открытия своей знаменитой теоремы Пифагор принес в жертву сто быков. С тех пор каждый раз, когда совершается открытие, крупный рогатый скот начинает волноваться.
Людвиг Бьорне
Вавилония и Египет Вавилония Источником наших знаний о вавилонской цивилизации служат хорошо сохранившиеся глиняные таблички, покрытые так…ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Тема 2: Элементы теории множеств
Основной уровень
1.1 F – множество фруктов. Принадлежит ли этому множеству: а) яблоко; б) арбуз; в) груша; г) апельсин; д) морковь; е) кокос. 1.2 S – множество спортивных игр. Принадлежит ли этому множеству: а) футбол;… 1.3 С – множество видов борьбы. Принадлежит ли этому множеству: а) дзюдо; б) самбо; в) каратэ; г) рестлинг; д) сумо;…Повышенный уровень
Задание 1. Определите, принадлежат ли объекты данному множеству: 1.1 М – множество предметов спортивного инвентаря. Принадлежит ли этому… 1.2 М – множество настольных игр. Принадлежит ли этому множеству: а) шахматы; б) шашки; в) домино; г) дартс; д) лото;…Основной уровень
1.1 а) Курган – столица России; б) Студент университета; в) Треугольник АВС подобен треугольнику А1В1С1; г) Луна – спутник Марса. 1.2 а) Кислород – газ; б) Каша – вкусное блюдо; в) Математика – интересный… 1.3 а) Железо тяжелее свинца; б) Да здравствуют музы!; в) Треугольник называется равносторонним, если все его стороны…Повышенный уровень
Задание 1.Укажите, какие из данных предложений являются высказываниями или высказывательными формами, не являются высказываниями или… 1.1 а) Число слов в этом предложении равно семи; б) В четырехугольнике… 1.2 а) Осень – лучшая пора года; б) Небо над Сицилией всегда голубое; в) Сожалею, но вы мне не нравитесь; г) Ни одно…Основной уровень
Задание 2.Вычислите а), б) , в) . (п – номер варианта)Повышенный уровень
Задание 2.Вычислите а), б) , в) . (п – номер варианта) Задание 3. Решите задачу:Основной уровень
Задание 1. Охарактеризуйте событие, о котором идет речь, как достоверное, невозможное или случайное: 1.1 А = «день рождения моего друга – число, меньше, чем 32». 1.2 А = «на уроке математики ученики делали физические упражнения».Повышенный уровень
1.1 Вы открыли эту книгу на любой странице и прочитали первое попавшееся существительное. Оказалось, что: а) в написании выбранного слова есть… 1.2 Даны два интервала (0; 1) и (5; 10). Из первого интервала выбрали число а,… 1.3 В мешке лежат 10 шаров: 3 синих, 3 белых и 4 красных. Оказалось, что: а) из мешка вынули 4 шара, и все они синие;…Основной уровень
Задание 1. После группировки данных эксперимента получилась таблица их распределения, с помощью которой: а) определите объем выборки; б) найдите… 1.1 Варианта -3 …Повышенный уровень
1.1 «…Это дерево – сосна,/И судьба сосны ясна…» 1.2 «…В траве сидел кузнечик,/Совсем как огуречик…» 1.3 «…Я помню, Огонь,/Как сжигал ты меня…»ВОПРОСЫ К ЭКЗАМЕНУ (зачету)
1. Какие понятия называют основными неопределяемыми понятиями? 2. Что значит определить понятие? 3. Что такое аксиома, теорема?Таблица
| Предпоследняя цифра зачетной книжки | Последняя цифра зачетной книжки | |||||||||
Продолжение таблицы
| Предпоследняя цифра зачетной книжки | Последняя цифра зачетной книжки | |||||||||
Контрольная работа оформляется в тетради в клеточку (12 листов). На титульном листе пишется название предмета (математика), фамилия, инициалы и номер группы студента, выполнившего работу.
Задания для контрольной работы
Задание 1: Даны множества: А и В. Найти: 1) А∩В; 2) АUВ; 3) АВ; 4) (АUВ)(А∩В).
1. А = {12; 20; 34; 37}, В = {2; 34; 35; 37}.
2. А = {3; 5; 7;9}, В = {3; 7; 15; 28}.
3. А = {2; 4; 6; 8; 10}, В = {2; 4; 3; 1; 6}.
4. А = {1; 2; 3; 4; 5; 6}, В = {3; 2; 6; 8}.
5. А = {25; 37; 44; 56}, В = {13; 15; 37; 48}.
6. А = {2; 6; 20; 21; 35}, В = {4; 15; 21; 35}.
7. А = {2; 3; 6; 8; 10}, В = {1; 2; 4; 25; 33}.
8. А = {0; 1; 2; 3; 7; 15}, В = {-2; 0; 3; 2; 14}.
9. А = {-7; -3; 2; 4; 33}, В = {-1; 0; 1; 2; 4; 3}.
10. А = {2; 6; 24; 12; 31}, В = {0; 7; 13; 18; 31}.
Задание 2: Решить задачу, используя формулу Грассмана:
11. В детском саду 52 ребенка. Каждый из них любит пирожное или мороженое. 25 детей любит пирожное, а 20 человек – пирожное и мороженое. Сколько детей любит мороженое?
12. Из 220 школьников 163 играют в баскетбол, 175 – в футбол, 24 – не играют в эти игры. Сколько человек играют в баскетбол и футбол?
13. Каждый из членов команды играет либо в футбол, либо в теннис, либо в футбол и в теннис. Сколько человек в команде, если известно, что 18 человек играют в обе игры, 23 человека играют в футбол, 21 – в теннис?
14. В кружке мягкой игрушки занимается 26 человек. Половина детей любят карамель, а 10 человек – карамель и шоколадные конфеты. Сколько детей любят шоколадные конфеты?
15. В младшей группе детского сада 15 детей пьют молоко, 20 – кефир, 10 – и молоко, и кефир. Сколько детей в группе?
16. Все студенты в группе изучают английский или немецкий язык. 12 студентов изучают английский язык, 15 – немецкий, 3 – оба языка. Сколько студентов в группе?
17. Из 27 учеников 13 человек любят читать фантастику, 8 – приключенческую литературу и фантастику. Сколько человек любят читать приключенческую литературу?
18. В кружке вязания 14 девочек связали шапочку, 15 – шарф, 7 – шапочку и шарф. Сколько девочек ходит в кружок?
19. В старшей группе детского сада 22 ребенка. Половина детей любит манную кашу, а 8 человек – и манную, и рисовую кашу. Сколько детей любит рисовую кашу?
20. В подготовительной группе детского сада 12 человек умеют читать, 13 – считать, 7 – читать и считать. Сколько человек в группе?
Задание 3: Формализовать высказывание:
21. «Если мистер Джонс счастлив, то миссис Джонс несчастлива, и если мистер Джонс несчастлив, то миссис Джонс счастлива».
22. «Если в Варшаву мы не поедем и в горы мы не отправимся, то ежедневно будем ходить на пляж или будем читать книги».
23. «Если «Спартак» проиграет, а «Торпедо» выиграет, то «Локомотив» потеряет первое место и на третье место выйдет «Зенит»».
24. «Если я поздно приду на остановку и не смогу сесть в автобус, то опоздаю на занятия и пропущу интересную лекцию».
25. «Если завтра будет воскресенье или в институте не будет занятий, то ко мне придут друзья и мы послушаем музыку».
26. «После обеда я отправлюсь на прогулку в парк или, если ко мне зайдет приятель, то я буду играть с ним в шахматы или мы посмотрим кино».
27. «Четырехугольник является параллелограммом тогда и только тогда, когда его диагонали пересекаются и в точке пересечения делятся пополам».
28. «Если в контрольной работе я выполнил первое и третье задания, то у меня есть шанс получить положительную отметку тогда и только тогда, когда я выполню второе задание».
29. «Если в пятницу не будет дождя или снега, то мы пойдем гулять или пойдем в кино».
30. «Две прямые параллельны тогда и только тогда, когда накрест лежащие углы равны или внутренние односторонние углы равны».
Задание 4: Проверить, равносильны ли формулы:
31. 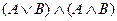 и
и 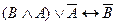 .
.
32. 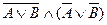 и
и 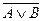 .
.
33. 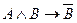 и
и 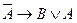 .
.
34. 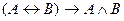 и
и 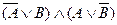 .
.
35. 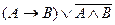 и
и 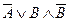 .
.
36. 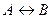 и
и 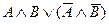 .
.
37. 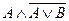 и
и 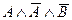 .
.
38. 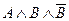 и
и 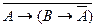 .
.
39. 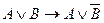 и
и 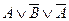 .
.
40. 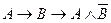 и
и 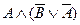 .
.
Задание 5:Решить задачу:
41. Первого сентября на первом курсе одного из факультетов запланировано по расписанию 3 лекции по разным предметам. Всего на первом курсе изучается 10 предметов. Сколько существует способов составить расписание на 1 сентября, если порядок предметов важен и если – не важен?
42. Сколькими способами можно из 15 солдат и 4 офицеров назначить в патруль трех солдат и одного офицера?
43. В некотором классе изучают 10 различных предметов. В пятницу завуч должен поставить 5 различных предметов. Сколькими способами он может это сделать, если порядок предметов важен и если – не важен?
44. В розыгрыше первенства по волейболу участвуют 12 команд. Сколько должно быть сыграно игр, если любые две команды должны сыграть между собой только один матч? Как изменится результат, если команды будут играть по 2 матча?
45. Сколько существует всего семизначных телефонных номеров, в каждом из которых ни одна цифра не повторяется; повторяется?
46. Из имеющихся семи роз и пяти веток зелени нужно составить букет, состоящий из трех роз и двух веток зелени. Сколькими способами можно составить такой букет?
47. В помещении 16 ламп. Сколько может быть различных вариантов освещения помещения, при котором должно гореть 12 ламп?
48. В вазе находятся разных по размерам 5 яблок и 6 апельсинов. Сколькими способами можно вынуть из вазы 2 яблока и 3 апельсина?
49. Каждый избиратель может занести в свой бюллетень либо одного, либо двух из 6 выдвигающихся на выборы кандидатов. Сколькими способами могут быть заполнены бюллетени?
50. Сколькими способами можно назначить патруль из двух солдат и одного офицера, если в роте имеются 80 солдат и 5 офицеров?
Задание 6:Решить задачу.
51. В ящике лежат 5 белых, 10 черных и 15 красных шаров. Какова вероятность того, что два наудачу вынутых шара будут белыми?
52. В пачке 12 билетов денежно-вещевой лотереи, 15 билетов лотереи РОСТО и 20 билетов художественной лотереи. Какова вероятность того, что наудачу вынутые два билета будут билетами денежно-вещевой лотереи?
53. В цехе работают 10 мужчин и 3 женщины. По табельным номерам наудачу выбраны 2 человека. Какова вероятность того, что выбранные люди окажутся мужчинами?
54. В цехе работают 10 мужчин и 3 женщины. По табельным номерам наудачу выбраны 2 человека. Какова вероятность того, что выбранные люди окажутся женщинами?
55. В цехе работают 10 мужчин и 3 женщины. По табельным номерам наудачу выбраны 2 человека. Какова вероятность того, что выбраны мужчина и женщина?
56. Студент, идя на экзамен, знал ответы на 70 вопросов из 90. Какова вероятность того, что студент ответит верно на предложенные ему экзаменатором 2 вопроса?
57. Школьник, идя на зачет, знал 15 из 20 предложенных к зачету вопросов. Какова вероятность того, что ему на зачете достанутся три известных ему вопроса?
58. В урне находятся 4 белых и 7 черных шаров. Какова вероятность того, что наудачу вынутые два шара окажутся белыми?
59. Из коробки, в которой имеется 4 желтых, 4 синих и 6 красных карандашей наудачу берут три карандаша. Какова вероятность того, что все карандаши синие?
60. В читальном зале есть 12 учебников по теории вероятностей, среди которых 4 новых. Наудачу берем 2 учебника. Найти вероятность того, что оба учебника новые.
Задание 7: Для данной выборки построить статистическое распределение выборки; построить полигон и гистограмму частот; дать характеристику распределения признака, вычислив для этого: 1) размах выборки; 2) медиану; 3) моду; 4) дисперсию; 5) математическое ожидание.
61. Для проведения демографических исследований выбрали 50 семей и получили следующие данные о количестве членов семьи: 2, 5, 3, 4, 1, 3, 6, 2, 4, 3, 4, 1, 3, 5, 2, 3, 4, 4, 3, 3, 2, 5, 3, 4, 4, 3, 3, 4, 4, 3, 2, 5, 3, 1, 4, 3, 4, 2, 6, 3, 2, 3, 1, 6, 4, 3, 3, 2, 1, 7.
62. Имеются следующие данные о размерах основных фондов 50 предприятий (в млн. руб.): 0,42; 0,24; 0,49; 0,45; 0,27; 0,42; 0,42; 0,5; 0,5; 0,5; 0,27; 0,25; 0,25; 0,49; 0,5; 0,42; 0,42; 0,49; 0,42; 0,24; 0,45; 0,42; 0,24; 0,49; 0,45; 0,27; 0,42; 0,5; 0,5; 0,42.; 0,42; 0,5; 0,27; 0,5; 0,49; 0,24; 0,27; 0,5; 0,45; 0,24; 0, 5; 0,42; 0,49; 0,25; 0,24; 0,3; 0,3; 0,5; 0,49; 0,42.
63. Известны данные о посевных площадях картофеля (тыс. гектаров) по районам Курганской области: 1,5; 1,5; 0,5; 1,2; 0,9; 0,9; 0,8; 0,5; 1,2; 1,1; 0,6; 1,1; 1,2; 0,9; 1,5; 1,2; 0,8; 0,4; 1,0; 0,1; 1,1; 0,8; 0,1; 1,5; 0,5; 1,2; 0,8; 0,3; 0,4; 1,3; 0,7; 0,1; 0,3; 1,6; 0,8; 0,7; 1,2; 1,5; 0,9; 0,6; 0,4, 1,0; 0,1; 1,0; 1,5; 1,2; 0,5; 1,3; 0,6; 0,8.
64. При сверлении отверстий одним и тем же сверлом и последующем измерении диаметров, получены следующие данные (в мм): 40,25; 40,35; 40,45; 40,35; 40,37; 40,35; 40,44; 40,35; 40,33; 40,41; 40,35; 40,30; 40,28; 40,30; 40,40; 40,36; 40,29; 40,33; 40,31; 40,33; 40,41; 40,40; 40,33; 40,37; 40,35; 40,34; 40,32; 40,34; 40,28; 40,46; 40,39; 40,37; 40,29; 40,39; 40,37; 40,44; 40,27; 40,38; 40,30; 40,32; 40,25; 40,36; 40,35; 40, 36; 40,33; 40,31; 40,29; 40,35; 40, 41; 40,30.
65. Имеются данные о величине латентного периода (в сек.) механического ответа при даче светового сигнала в первом предъявлении: 0,35; 0,54; 0,33; 0,33; 0,36; 0,61; 0,23; 0,25; 0,48; 0,28; 0,57; 0,29; 0,29; 0,41; 0,35; 0,36; 0,51; 0,74; 0,35; 0,44; 0,29; 0,36; 0,34; 0,34; 0,38; 0,31; 0,33; 0,32; 0,37; 0,30; 0,36; 0,35; 0,37; 0,35; 0,40; 0,37; 0,39; 0,39; 0,53; 0,45; 0,28; 0,34; 0,23; 0,44; 0,29; 0,35; 0,30; 0,37; 0,41; 0,28.
66. Имеются данные о размерах резервных фондов (в млн. руб.) 50 предприятий: 0,42; 0,24; 0,49; 0,47; 0,42; 0,24; 0,49; 0,24; 0,49; 0,40; 0,28; 0,72; 0,42; 0,47; 1,21; 0,42; 0,47; 0,48; 1,21; 0,48; 0,49; 0,72; 0,46; 0,28; 0,46; 1,21; 0,46; 1,21; 0,72; 0,49; 0,43; 0,24; 0, 47; 0,42; 1,21; 0,72; 0,88; 0,88; 1,21; 0,24; 0,28; 0, 49; 0,46; 0,24; 0,72; 0,43; 0,42; 0,47; 0,43; 0,46.
67. Имеются данные измерения длины плеча (в мм) мухоловки пеструшки на 5-й день жизни: 13,7; 14,3; 10,3; 13,0; 13,0; 12,0; 17,3; 13,0; 12,3; 10,4; 14,0; 11,3; 16,3; 11,7; 13,0; 10,4; 15,0; 14,1; 13,1; 16,3; 11,6; 11,5; 13,2; 14,3; 13,5; 10,4; 12,3; 11,3; 11,0; 13,1; 13,7; 13,1; 11,7; 13,0; 10,4; 15,0; 14,3; 11,6; 13,2; 12,0; 14,3; 11,3; 14,3; 11,6; 12,0; 16,3; 10,4; 15,0; 13,2; 11,7.
68. Имеются данные измерения величин интенсивности порогового раздражения глаз при длительности дачи света в 0,002 сек: 0,76; 2,37; 2,37; 3,14; 4,45; 4,71; 4,81; 4,81; 5,08; 5,08; 6,27; 1,29; 1,29; 1,29; 1,64; 1,56; 1,56; 1,64; 1,29; 1,56; 1,64; 1,64; 2,20; 2,11; 2,11; 2,11; 2,20; 3,14; 4,71; 4,45; 4,45; 3,28; 3,28; 3,14; 2,37; 2,20; 2,11; 2,20; 2,37; 2,37; 2,20; 3,20; 3,20; 3,11; 3,14; 3,28; 2,11; 2,37; 3,14; 2,37.
69. Имеются данные наблюдения за числом посетителей сайта университета в течение 50 дней: 70, 75, 100, 120, 75, 60, 100, 120, 70, 60, 65, 100, 65, 100, 70, 75, 60, 100, 100, 120, 70, 75, 70, 120, 65, 70, 75, 70, 100, 100, 120, 120, 100, 75, 75, 70, 70, 100, 100, 75; 75; 100; 120; 65; 100; 75; 75; 60; 120; 70.
70. Имеются данные результатов тестирования 50 студентов по математике (ответы на 50 вопросов программы): 33, 42, 27, 33, 23, 26, 31, 43, 45, 44, 16, 36, 19, 19, 23, 43, 49, 25, 22, 23, 28, 36, 36, 28, 43, 45, 21, 48, 49, 44; 15; 31; 45; 43; 44; 16; 23; 43; 25; 48; 28; 36; 44; 43; 22; 22; 16; 33; 31; 16.
Образец решения контрольной работы
Вариант 0
Задание 1: Даны множества: А и В. Найти: 1) А∩В; 2) АUВ; 3) АВ; 4) (АUВ)(А∩В).
Решение.
А = {3, 2, 5, 7, 8, 11}, B = {1, 2, 3, 4, 5}. В соответствии с определениями операций над множествами найдем их пересечение, объединение, разность и разность множеств, являющихся их объединением и пересечением:
1) А∩В = {3, 2, 5}. Так как в пересечение множеств включаются только общие элементы.
2) АUВ = {3, 2, 5, 7, 8, 11, 1, 4}. Так как в объединение входят все элементы множеств, встречающиеся хотя бы один раз.
3) АВ = {7, 8, 11}. Так как в разность входят те элементы первого множества, которых нет во втором.
4) (АUВ)(А∩В) = {7, 8, 11, 1, 4}.
Задание 2: Решить задачу, используя формулу Грассмана:
Из 40 учащихся класса 32 выписывают газету, 21 – журнал, 15 учащихся – и газету и журнал. Сколько учащихся не выписывают ни газету, ни журнал?
Решение.
Переведем задачу на язык множеств и изобразим ситуацию с помощью диаграмм Эйлера-Венна. Обозначим через Е множество всех учеников класса, через А – множество выписывающих газету и через В – множество выписывающих журнал.
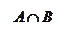


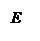
 Тогда |E| = 40, |A| = 32, |B| = 21, |AÇB| = 15. Требуется найти, чему равно |E(AÈB)| (закрашено желтым цветом). Сначала найдем, чему равно |AÈB|, подставив известные значения в формулу Грассмана: |AÈB| = |А| + |B| - |AÇB| = 32 + 21 – 15 = 38. Теперь
Тогда |E| = 40, |A| = 32, |B| = 21, |AÇB| = 15. Требуется найти, чему равно |E(AÈB)| (закрашено желтым цветом). Сначала найдем, чему равно |AÈB|, подставив известные значения в формулу Грассмана: |AÈB| = |А| + |B| - |AÇB| = 32 + 21 – 15 = 38. Теперь 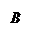 найдем |E(AÈB)|. |E(AÈB)| =|E| - |AÈB| = 40 – 38 = 2. Таким образом, 2 ученика не выписывают ни газету, ни журнал.
найдем |E(AÈB)|. |E(AÈB)| =|E| - |AÈB| = 40 – 38 = 2. Таким образом, 2 ученика не выписывают ни газету, ни журнал.
Задание 3: Формализовать высказывание: Е = «Лошадь погибает от одного грамма никотина, но я не лошадь, следовательно, курить вредно».
Решение.
Переформулируем высказывание так, чтобы все логические связки оказались в явном виде: Если лошадь погибает от одного грамма никотина и я не лошадь, то курить вредно.
Обозначим через А: «лошадь погибает от одного грамма никотина»; через В: «я не лошадь»; через С: «курить вредно». Прочитаем теперь будущую формулу, не используя текстовые высказывания: Если А и В, то С. Теперь заменим логические связки соответствующими символами логических операций: 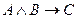 . Полученная формула является искомой.
. Полученная формула является искомой.
Задание 4: Проверить, равносильны ли формулы: G = 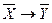 ; H =
; H = 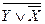 .
.
Решение.
Для проверки построим для каждой формулы таблицу истинности и сравним результаты в итоговых столбцах.
Для формулы G = 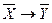 :
:
| Х | Y | 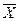
| 
| 
|
Для формулы H = 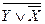 :
:
| Х | Y | 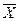
| 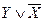
| 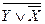
|
Так как в соответствующих строках (то есть при соответствующих наборах значений переменных) в итоговых столбцах стоят разные значения, то формулы неравносильны.
Задание 5:Решить задачу: По списку в 9 классе 15 девочек и 13 мальчиков. Нужно выбрать двух дежурных по классу. Сколькими способами это можно сделать:
а) при условии, что пару обязательно должны составить мальчик и девочка;
б) без указанного условия?
Решение.
а) Так как пару должны обязательно составить мальчик и девочка, то при составлении пары мы выбираем одного мальчика из 13 и одну девочку из 15. При этом порядок выбора не важен. Можем воспользоваться формулой сочетаний или использовать правило умножения: 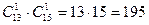 . То есть всего 195 пар, которые будут состоять из одного мальчика и одной девочки.
. То есть всего 195 пар, которые будут состоять из одного мальчика и одной девочки.
б) Теперь пара составляется без учета первого условия, то есть мы выбираем любых двух человек из 28 и порядок при этом не важен. Поэтому воспользуемся формулой сочетаний:
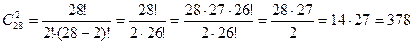 . Ответ: всего 378 пар.
. Ответ: всего 378 пар.
Задание 6:Решить задачу: В коробке «Ассорти» – 20 неразличимых по виду конфет, из которых 12 с шоколадной начинкой и 8 с фруктовой начинкой. Тане разрешили взять две конфеты. Какова вероятность того, что конфеты – с фруктовой начинкой?
Решение.
Задачу можно решить двумя способами (при решении контрольной работы нужно выбрать только один из них).
1 способ: Испытание состоит в том, что мы вынимаем 2 конфеты из коробки. Случайное событие А состоит в том, что обе конфеты с фруктовой начинкой. Общее число равновозможных исходов п – это число всех пар, которые мы можем составить из конфет, лежащих в коробке. Так как порядок конфет в парах не важен, то воспользуемся формулой сочетаний: 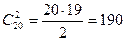 . Количество исходов, благоприятствующих наступлению события А (тА) – это число всех пар, которые можно составить из конфет с фруктовой начинкой. Снова воспользуемся формулой сочетаний и получим, что тА = 28. Тогда вероятность наступления события А находится по формуле:
. Количество исходов, благоприятствующих наступлению события А (тА) – это число всех пар, которые можно составить из конфет с фруктовой начинкой. Снова воспользуемся формулой сочетаний и получим, что тА = 28. Тогда вероятность наступления события А находится по формуле: 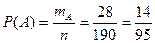 .
.
2 способ: Испытание состоит в том, что мы берем конфеты по одной (по очереди). Разделим событие А на два: А1 – первой вынута конфета с фруктовой начинкой и А2 – второй вынута конфета с фруктовой начинкой. Тогда наступление второго события зависит от наступления первого. Можно воспользоваться теоремой об условной вероятности. Так как нам надо найти вероятность одновременного появления двух событий, наступление одного из которых зависит от наступления другого, то формула для нахождения вероятности имеет вид: 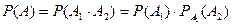 . Найдем значение каждого из множителей. Так как мы выбираем одну конфету, то п = 20, а тА1 = 8. Тогда
. Найдем значение каждого из множителей. Так как мы выбираем одну конфету, то п = 20, а тА1 = 8. Тогда 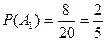 . Вероятность второго события находим, учитывая, что событие А1 уже произошло: п = 19, а тА2 = 7. Тогда
. Вероятность второго события находим, учитывая, что событие А1 уже произошло: п = 19, а тА2 = 7. Тогда 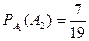 . Находим искомую вероятность:
. Находим искомую вероятность: 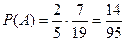 . Получили тот же ответ, что и при решении задачи первым способом.
. Получили тот же ответ, что и при решении задачи первым способом.
Задание 7: Для данной выборки построить статистическое распределение выборки; построить полигон и гистограмму частот; дать характеристику распределения признака, вычислив для этого: а) размах выборки; б) медиану; в) моду; г) дисперсию; д) математическое ожидание.
Имеются данные результатов контрольного теста по математике студентов специальности ФКиС (из 100 баллов): 15, 20, 6, 6, 24, 20, 16, 13, 13, 10, 9, 6, 19, 22, 3, 6, 6, 10, 6, 13, 21, 3, 3, 11, 3, 17, 3, 6, 3, 3, 26, 36, 15, 14, 9, 27, 19, 16, 20, 9.
Решение.
Дана выборка объема 40 (столько перечислено вариант). Запишем сначала вариационный ряд: 3, 6, 9, 10, 11, 13, 14, 15, 16, 17, 19, 20, 21, 22, 24, 26, 27, 36. Составим таблицу распределения вариант:
| Варианта, хi | Кратность варианты | Частота варианты, рi | Частота (%) варианты | хi – М(Х) |
| 0,175 | 17,5 | -9,825 | ||
| 0,175 | 17,5 | -6,825 | ||
| 0,075 | 7,5 | -3,825 | ||
| 0,05 | -2,825 | |||
| 0,025 | 2,5 | -1,825 | ||
| 0,075 | 7,5 | 0,175 | ||
| 0,025 | 2,5 | 1,175 | ||
| 0,05 | 2,175 | |||
| 0,05 | 3,175 | |||
| 0,025 | 2,5 | 4,175 | ||
| 0,05 | 6,175 | |||
| 0,075 | 7,5 | 7,175 | ||
| 0,025 | 2,5 | 8,175 | ||
| 0,025 | 2,5 | 9,175 | ||
| 0,025 | 2,5 | 11,175 | ||
| 0,025 | 2,5 | 13,175 | ||
| 0,025 | 2,5 | 14,175 | ||
| 0,025 | 2,5 | 23,175 |
Размах выборки – это разница между наибольшей и наименьшей вариантой: 36 – 3 = 33.
Медиана – это варианта, которая находится «посередине» выборки или среднее арифметическое значение «серединных» вариант. Так как вариационный ряд состоит из 18 элементов, то медианой выборки будет число, равное среднему арифметическому чисел 16 и 17: 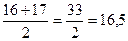 .
.
Мода – это варианта, которая встречается чаще всех. В нашей выборке таких вариант две: 3 и 6, то есть наша выборка – бимодальная.
Для вычисления математического ожидания воспользуемся формулой: 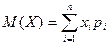 .
.
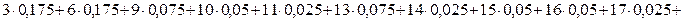
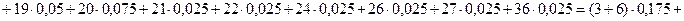
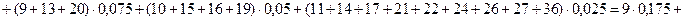
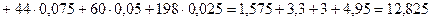 .
.
Тогда М(Х) = 12,825.
Для вычисления дисперсии, то есть величины рассеяния случайной величины Х, воспользуемся формулой: 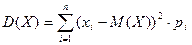 . Сначала добавим в таблицу еще один столбец, в котором запишем результаты вычисления разности хi – М(Х), а затем подставим найденные значения в формулу дисперсии:
. Сначала добавим в таблицу еще один столбец, в котором запишем результаты вычисления разности хi – М(Х), а затем подставим найденные значения в формулу дисперсии:
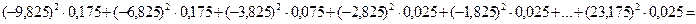 = 63,291875 » 63,29.
= 63,291875 » 63,29.
Осталось нарисовать полигон (многоугольник) и гистограмму частот.
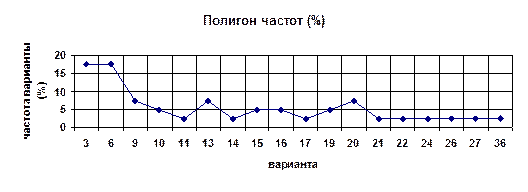
Для того, чтобы изобразить гистограмму частот, разобьем вариационный ряд на три части: [1; 12], [13; 24] и [25; 36] (интервальный ряд данных). Для каждой из этих частей найдем сумму всех кратностей и процентную частоту промежутка. Получим таблицу:
| Варианта | [1; 12] | [13; 24] | [13; 24] |
| Кратность варианты | |||
| Частота (%) | 42,5 | 7,5 |
Тогда гистограмма (столбчатая диаграмма) будет иметь вид:

ЛИТЕРАТУРА
1. Ван-дер-Варден Б.Л. Пробуждающаяся наука. Математика Древнего Египта, Вавилона и Греции. М., 1959.
2. Гаврилова О.А. Математические методы и модели в социально-правовом исследовании – М., Наука, 1980г.
3. Грес П.В. Математика для гуманитариев. Учебное пособие. – М.: Логос, 2003.
4. Даан-Дальмедико А., Пейффер Ж. Пути и лабиринты. Очерки по истории математики. М., 1986.
5. Клейн Ф. Лекции о развитии математики в XIX столетии. М., 1989.
6. Математические модели природы и общества / Калиткин Н.Н., Карпенко Н.В., Михайлов А.П., Тишкин В.Ф., Черненков М.В. - М.: ФИЗМАТЛИТ, 2005. - 360 с.
7. Мордкович А.Г., Семенов П.В. События. Вероятности. Статистическая обработка данных: Доп. параграфы к курсу алгебры 7-9 кл. общеобразоват. учреждений. – 3-е изд. – М.: Мнемозина, 2005.
8. Никольская И.Л. Знакомство с математической логикой. – М.: Московский психолого-социальный институт: Флинта, 1998.
9. Погорелов А.В. Геометрия: Учеб. для 7-11 кл. общеобразоват. учреждений. – М.: 1998.
10. Скворцова М. Математическое моделирование// Математика – приложение к газете «Первое сентября» – 2003. - № 14 – С. 1-4.
11. Шелобаев С.И. Математические методы и модели. – ЮНИТИ – 2001, 367 с.
12. Шикин Е, Шикина Г. Гуманитариям о математике. Рассказ третий. Модели// Математика – приложение к газете «Первое сентября» – 1999. - № 43 – С. 19-25.
13. Юшкевич А.П. История математики в средние века. М., 1961.
14. http://olddesign.isu.ru/~slava/do/disc/arithmet.htm
15. http://gatchina3000.ru/great-soviet-encyclopedia/bse/007/395.htm
16. http://neuronet.alo.ru/phenomenon/chapter12.htm#12.09
17. http://promo.ntv.ru/gordon/archive/12510/
18. http://gabro.ge/biblio/0707/3066/filosof.historic.ru/books/item/f00/s00/z0000616/index.htm
19. http://www.monax.ru
20. http://refhist.ru/history/mathematical_methods_and_models_in_legal_research/m/28386/1.1.html
21. http://ardis.hi-edu.ru/e-books/xbook081/01/index.html?part-003.htm#i321
22. http://readall.ru/lib_page_readall_109323.html
СОДЕРЖАНИЕ
| Введение ………………………………………………………… | |
| Памятка студенту ………………………………………………. | |
| Тема 1: Аксиоматический метод ………………………………. | |
| Тема 2: Элементы теории множеств …………………………… | |
| Тема 3: Элементы математической логики …………………… | |
| Тема 4: Элементы комбинаторики …………………………….. | |
| Тема 5: Элементы теории вероятностей ………………………. | |
| Тема 6: Элементы математической статистики ………………. | |
| Тема 7: Элементы математического моделирования ………… | |
| Тема 8: Элементы истории математики ………………………. | |
| Задачи для самостоятельного решения ……………………….. | |
| Темы рефератов ………………………………………………… | |
| Задания исследовательского характера ………………………. | |
| Вопросы к экзамену (зачету) …………………………………... | |
| Контрольная работа для студентов заочного отделения …….. | |
| Литература ……………………………………………………… |
– Конец работы –
Используемые теги: Учебное, пособие, предназначено, студентов, гуманитарных, специальностей, изучающих, математику, технологии, индивидуализированного, обучения0.119
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Учебное пособие предназначено для студентов гуманитарных специальностей, изучающих математику по технологии индивидуализированного обучения
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов