рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Философия
- /
- ТЕОРИЯ ВЕРОЯТНОСТЕЙ В ЗАДАЧАХ
Реферат Курсовая Конспект
ТЕОРИЯ ВЕРОЯТНОСТЕЙ В ЗАДАЧАХ
ТЕОРИЯ ВЕРОЯТНОСТЕЙ В ЗАДАЧАХ - раздел Философия, Министерство Образования Республики Беларусь ...
Министерство образования Республики Беларусь
БЕЛОРУССКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра «Высшая математика № 2»
ТЕОРИЯ ВЕРОЯТНОСТЕЙ В ЗАДАЧАХ
НАДЕЖНОСТИ УСТРОЙСТВ И СИСТЕМ
лекции
М и н с к 2 0 12
УДК 519.85 (075.8)
ББК 18.87я7
М 54
Составители: А.Н. Рудый
Рецензенты:
В.В. Карпук, В.В.Павлов
© БНТУ, 2012
Вероятностное пространство
Замечание. Ω – это произвольное множество, U – алгебра событий (совокупность подмножеств множества Ω, замкнутая относительно операций… 1) 2)Упражнения
1.1. Найти вероятность безотказной работы схемы, логические модели которых: а)Случайные величины.
Определение 1. Пусть - вероятностное пространство. Действительно-значную функцию , определенную на Ω будем называть случайной величиной (для… Замечание.Среди непрерывных СВ будем рассматривать абсолютно-непрерывные, а… (1)Замечание. .
Решение. Пусть СВ Х – число работающих исправно в течение времени t блоков. Тогда по формуле (8): 1) . 2) .Замечание. .
. (10) Замечание. Из теоремы 1 следует, что распределение Пуассона – предельный… Пример 2.Радиоэлектронная система (РЭС) состоит из 200 узлов. Вероятность отказа каждого из них за время t равна…Упражнения.
1) система будет работать; 2) система откажет. Ответ 2.1: 1) 0,73728, 2) 0,26272.Основные понятия теории надежности.
Определение 1.Пусть СВ Т 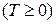 задает момент времени выхода из строя элемента (время наработки на отказ, или время жизни). Функцию распределения
задает момент времени выхода из строя элемента (время наработки на отказ, или время жизни). Функцию распределения  будем называть функцией ненадежности (
будем называть функцией ненадежности (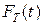 задает вероятность отказа элемента на промежутке [0 ; t)). Функцию
задает вероятность отказа элемента на промежутке [0 ; t)). Функцию
 (1)
(1)
будем называть функцией надежности ( p(t) задает вероятность того, что элемент откажет на промежутке  , или его время жизни
, или его время жизни 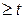 ).
).
Пример 1.Вероятность того, что изделие работало безотказно на промежутке времени [ 0; 4500) равна 0,406. Предположим, что время жизни Т распределено по экспоненциальному закону. 1) Найти Тср – среднее время жизни. 2) Найти вероятность того, что изделие будет исправно при t = Tср .
Решение. 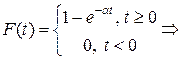 по формуле (1)
по формуле (1) 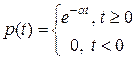 .(2)
.(2)
Тогда 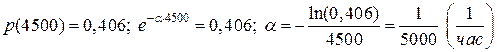 .
.
1) 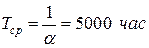 .
.
2)  .
.
Замечание.1. Так как  , то
, то 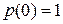 .
.
2. Так как 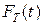 - неубывающая функция и
- неубывающая функция и  , то p(t) – невозрастающая функция и
, то p(t) – невозрастающая функция и  .
.
Пример 2. Пусть Т распределена по закону 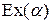 ,
,
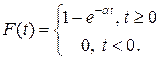 Тогда
Тогда 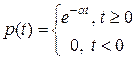 .
.
Приведем графики p(t) для 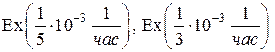 .
.
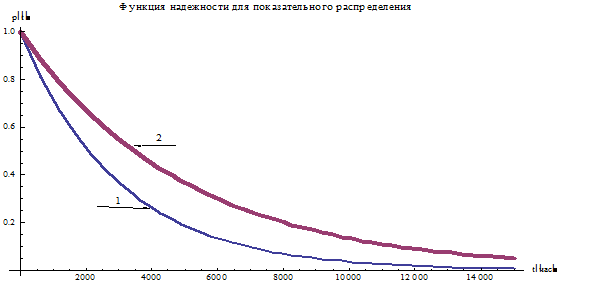
Рис. 1. Графики p(t) для экспоненциальных распределений 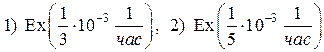 .
.
Пример 3. Пусть Т распределена по закону  ,
,
 , тогда
, тогда  , где
, где 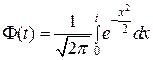 .
.
Приведем графики p(t) для N(5000 час, 1500 час) и N(5000 час, 500 час).

Рис 2. Графики p(t) для 1) N(5000 час, 1500 час) и 2) N(5000 час, 500 час).
Определение 2. Условная плотность вероятности отказа элемента в момент времени t, при условии, что на промежутке 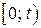 он работал безотказно, называется интенсивностью отказа элемента в момент времени t . Интенсивность отказа обозначим через
он работал безотказно, называется интенсивностью отказа элемента в момент времени t . Интенсивность отказа обозначим через 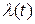 . Таким образом
. Таким образом 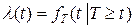 .
.
Замечание.  равно, при небольших
равно, при небольших  , вероятности того, что элемент, проработав безотказно на промежутке
, вероятности того, что элемент, проработав безотказно на промежутке 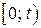 , откажет на промежутке
, откажет на промежутке  . При этом
. При этом  равно вероятности отказа элемента на промежутке
равно вероятности отказа элемента на промежутке  , независимо от того работоспособен он или нет в момент времени t.
, независимо от того работоспособен он или нет в момент времени t.
Теорема 1.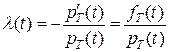 . (3)
. (3)
Доказательство. Пусть 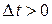 , событие А – элемент откажет на промежутке
, событие А – элемент откажет на промежутке  , событие В – элемент откажет на промежутке
, событие В – элемент откажет на промежутке 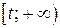 (то есть безотказно проработает на промежутке
(то есть безотказно проработает на промежутке 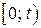 ). Тогда
). Тогда 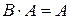 и
и
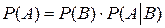 , (4)
, (4)
но 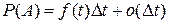 ,
, 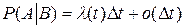 ,
, 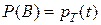 , где
, где 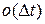 - бесконечно-малая более высокого порядка малости, чем
- бесконечно-малая более высокого порядка малости, чем  , при
, при  . Подставив найденные производные в формулу (4), получим
. Подставив найденные производные в формулу (4), получим
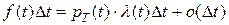
 и в пределе при
и в пределе при 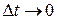 , получим
, получим 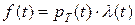 ч.т.д.
ч.т.д.
Упражнение. Доказать, что для экспоненциального распределения 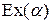 интенсивность отказов
интенсивность отказов 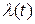 – постоянна и
– постоянна и  .
.
Замечание. При статистическом оценивании значений  и
и  число отказавших элементов на промежутке
число отказавших элементов на промежутке  делят на число всех испытуемых ( при оценивании
делят на число всех испытуемых ( при оценивании  ) и на число исправных к моменту времени t (при оценивании
) и на число исправных к моменту времени t (при оценивании  ).
).
Интенсивность отказов 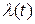 является важным показателем надежности. Его нетрудно оценить статистически и он дает наглядное представление о поведении объекта исследования. Показатель
является важным показателем надежности. Его нетрудно оценить статистически и он дает наглядное представление о поведении объекта исследования. Показатель 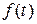 менее нагляден.
менее нагляден.
Например, рассмотрим промежуток  и
и 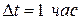 , тогда
, тогда 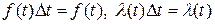 . Тогда для распределений
. Тогда для распределений 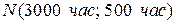 и
и  (распределение Вейбулла, см. § ) графики
(распределение Вейбулла, см. § ) графики 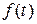 и
и 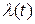 будут иметь вид:
будут иметь вид:
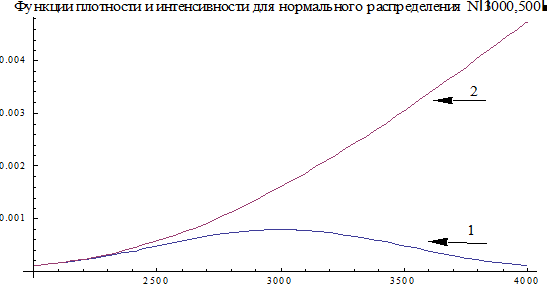
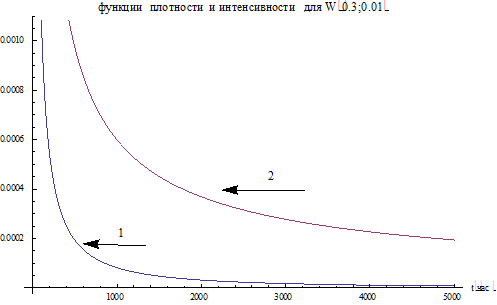
Рис.3. Графики 1) 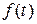 и 2)
и 2) 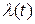 .
.
График функции 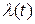 имеет во многих случаях типичную U – образную форму. Например, для системы, логическая модель надежности которой:
имеет во многих случаях типичную U – образную форму. Например, для системы, логическая модель надежности которой:

1 2 , причем
время жизни первого элемента  (распределение Вейбулла, см. §7, п. 7.4), а второго –
(распределение Вейбулла, см. §7, п. 7.4), а второго – 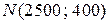 , график
, график 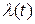 имеет вид
имеет вид
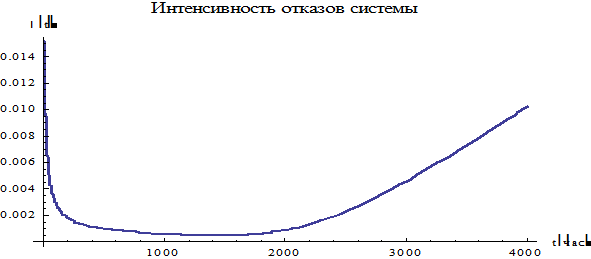
Рис.4. График функции 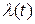 интенсивности отказов системы.
интенсивности отказов системы.
Замечание.Отказы на промежутке 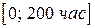 - приработочные, отказы на промежутке
- приработочные, отказы на промежутке 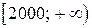 вызваны старением.
вызваны старением.
Выпишем зависимости между показаниями надежности 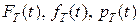 и
и 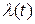 .
.
1. 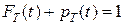 (5)
(5) 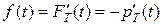 (6)
(6)
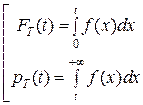 (7)
(7)
2.  (см. теорему 1).
(см. теорему 1).
3. Выразим p(t) через 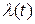 . Для этого решим дифференциальное уравнение (3), с начальными данными
. Для этого решим дифференциальное уравнение (3), с начальными данными 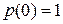 .
.
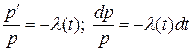
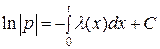
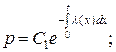 так как
так как 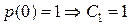 .
.
Таким образом:
 . (8)
. (8)
Найдем еще 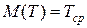 - среднее время наработки на отказ (среднее время жизни)
- среднее время наработки на отказ (среднее время жизни)
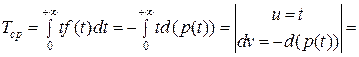
 .
.
Из физических соображений считаем, что 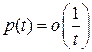 , при
, при  .
.
Таким образом:
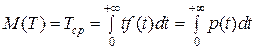 . (9)
. (9)
Аналогично 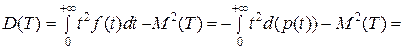
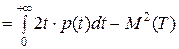 . (10)
. (10)
Упражнения.
Выписать: 1) функцию плотности вероятностей , 2) функция распределения , 3) функцию надежности ,Статистическое оценивание показателей надежности.
Пусть на промежутке времени испытывается N0 одинаковых элементов. Разобьем промежуток на n частичных промежутков одинаковой длины точками . Пусть -… , (1) , (2)Упражнения.
Найти . а) Интервалы времени (час) 0 - 100 100 - 200 200 -…Показатели надежности для сложных систем.
5.1.Техническая система может быть невосстанавливаемой и восстанавливаемой. В последнем случае она продолжает работу после устранения отказа. При… Для повышения надежности системы применяют структурное резервирование, когда в… Можно также резервировать элементы подсистем в системе. Кратность в различных резервируемых подсистемах может быть…Пример 1.
| Тип резервирования | Логическая схема | Комментарий | |
| Общее резервирование, постоянно включенный резерв | 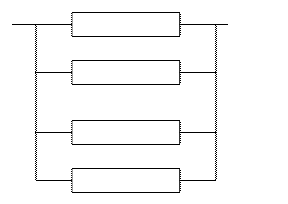 0
Осн. устр. 0
Осн. устр.
| Целая кратность 3 | |
| Резервирование замещением |  Осн. устр.
Осн. устр.
| Целая кратность 3 | |
| Поэлементное, с постоянным резервом |  1 2 3
0 0 0
1 1 1
2 2 2
1 2 3
0 0 0
1 1 1
2 2 2
| Целая кратность 2 | |
| Поэлементное, замещением |  0 0 0
1 1 1
0 0 0
1 1 1
| Целая кратность 1 | |
| Тип резервирования | Логическая схема | Комментарий | |
| Поэлементное, с постоянным резервом |
 01 02
11 12
01 02
11 12
| Для элемента 01 – целая кратность 2, для элемента 02 – целая кратность 1 | |
| Поэлементное, с постоянным резервом | 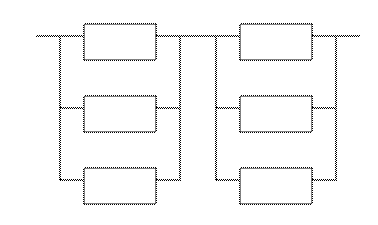 0 0
0 0
1 1
0 0
0 0
1 1
| Дробная кратность 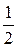
| |
Замечание.В случае резервирования замещением резервные элементы подключаются после отказа соответствующих основных.


 Элементы 01 , 02 ,
Элементы 01 , 02 ,

0 , в таблице соответствуют основному устройству.
5.2. Рассмотрим нерезервированную невосстанавливаемую систему, логическая модель надежности которой:
1 2 n
Тогда функция надежности системы:
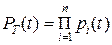 , (1)
, (1)
где 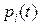 - функция надежности i – ого элемента. Если
- функция надежности i – ого элемента. Если 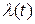 и
и 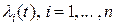 функции интенсивности отказов системы и ее элементов, то, используя формулу (8) § 3, получим
функции интенсивности отказов системы и ее элементов, то, используя формулу (8) § 3, получим
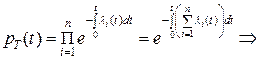
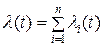 , (2)
, (2)
то есть при последовательном соединении элементов интенсивности их отказов суммируются и дают интенсивность отказов системы.
В частности, если  (распределения
(распределения 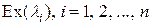 ), то из формулы (2) следует
), то из формулы (2) следует
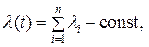 (3)
(3)
то есть время жизни системы также распределено экспоненциально, при этом среднее время жизни
 . (4)
. (4)
Пример 2.Нерезервированная система состоит из 3-х последовательно соединенных элементов. Время жизни элементов – экспоненциальное: 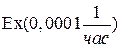 ,
, 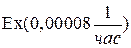 ,
, 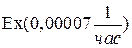 . Определить показатели надежности системы:
. Определить показатели надежности системы: 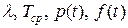 .
.
Решение. По формулам (1) – (4):
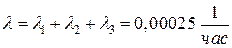 .
.
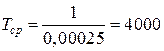 час
час
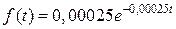
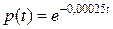 .
.
5.3.Рассмотрим резервированную невосстанавливаемую систему с постоянно включенным резервом кратности n:
 0
0
n
Тогда функция ненадежности системы:
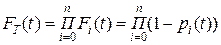 , (5)
, (5)
где 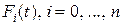 - функции ненадежности элементов.
- функции ненадежности элементов.
Тогда 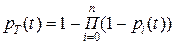 , (6)
, (6)
где 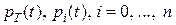 - функция надежности системы и ее элементов.
- функция надежности системы и ее элементов.
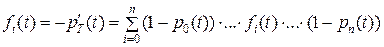 (7)
(7)
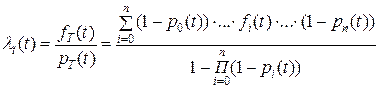 . (8)
. (8)
Замечание. Из формулы (8) видно, что если время жизни элементов распределено по экспоненциальным законам, то время жизни системы не будет экспоненциальным.
Предположим, что 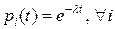 , тогда
, тогда  . Найдем
. Найдем 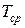 . По формуле (8) § 3:
. По формуле (8) § 3:

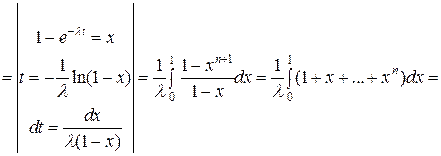
 . (9)
. (9)
Резервирование естественно предполагает повышение надежности системы. Выигрыш от введения резерва можно определить введя коэффициенты:
 - выигрыш в надежности по Тср,
- выигрыш в надежности по Тср,
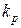 - выигрыш в надежности по вероятности безотказной работы p(t),
- выигрыш в надежности по вероятности безотказной работы p(t),
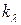 - выигрыш в надежности по интенсивности отказов
- выигрыш в надежности по интенсивности отказов 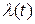 .
.
А именно,
 =
= , (10)
, (10)
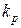 =
=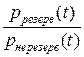 , (11)
, (11)
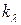 =
= . (12)
. (12)
Пример 3.Резервированная невосстанавливаемая система состоит из 3-х параллельно соединенных элементов (постоянно включенный резерв кратности 2). Время жизни каждого элемента 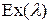 .
.
1) Определить показатели надежности системы: 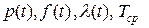 .
.
2) Определить выигрыш в надежности  ,
, 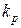 ,
, 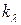 .
.
Решение. По формуле (6)
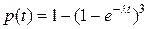 . Поэтому
. Поэтому
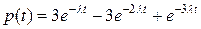 ,
, 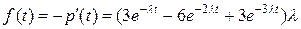
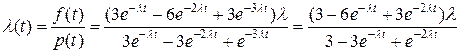 .
.
По формуле (9)
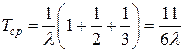 .
.
2) По формулам (10) – (12):
 =
= =
=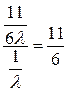 ;
;
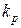 =
= =
= ;
;
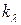 =
= =
=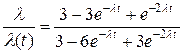 .
.
Из расчетов видно, что 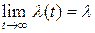 и
и 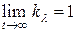 ;
;  .
.
Замечание. Рассмотрим формулу (6) и предположим, что 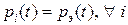 , тогда
, тогда 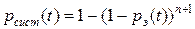 ;
; 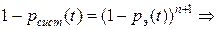 получим формулу
получим формулу
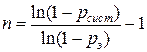 , (13)
, (13)
которую можно использовать для нахождения кратности резервирования, которая бы обеспечивала необходимые показатели надежности системы.
Пример 4. Время наработки элемента на отказ 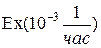 . Определить кратность его резервирования такими же элементами, чтобы вероятность безотказной работы системы в течение t=1000 час была 0.9.
. Определить кратность его резервирования такими же элементами, чтобы вероятность безотказной работы системы в течение t=1000 час была 0.9.
Решение. 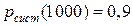 .
.  .
. 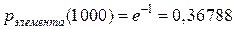 . Тогда по формуле (13)
. Тогда по формуле (13)  .
.
Округляя в большую сторону, получим n=5.
Замечание. Необходимо отметить, что с ростом t кратность резервирования возрастает. Например, для вероятности p=0,9 и распределения 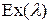 :
:
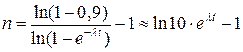 .
.
5.4. Рассмотрим резервированную невосстанавливаемую систему (резерв кратности 1, замещением):

Пусть f0 (t), f1 (t) – функции плотности вероятностей распределения времени наработки на отказ элементов; р0 (t), р1 (t) – функции надежности элементов, f(t), p(t) – аналогичные функции для системы. Тогда Т – время наработки системы на отказ: 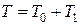 , где Т0, Т1 – время наработки на отказ элементов. Найдем p(t). Рассмотрим промежуток [0, t ) и разобьем его на n частичных промежутков длины
, где Т0, Т1 – время наработки на отказ элементов. Найдем p(t). Рассмотрим промежуток [0, t ) и разобьем его на n частичных промежутков длины  . Отказ 0 –ого элемента может произойти на любом из этих частичных промежутков. Пусть сi – точка отказа на i-ом промежутке. Тогда по формуле полной вероятности:
. Отказ 0 –ого элемента может произойти на любом из этих частичных промежутков. Пусть сi – точка отказа на i-ом промежутке. Тогда по формуле полной вероятности:
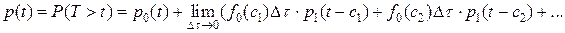
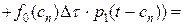
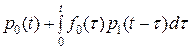 (10)
(10)
или 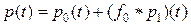 , (11)
, (11)
где 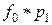 - свертка функций
- свертка функций 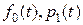 .
.
Далее 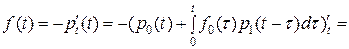
=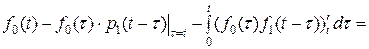
= .
.
Таким образом 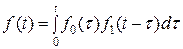 , (12)
, (12)
или 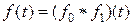 . (13)
. (13)
Аналогично, для резервирования замещением кратности n:
 0
0
n
Получаем формулы:
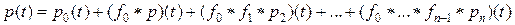 (14)
(14)
и 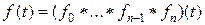 . (15)
. (15)
p(t) можно находить такие же и по формуле
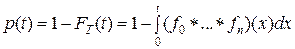 . (16)
. (16)
Пример 5. Рассмотрим резервированную невосстанавливаемую систему (резерв замещением, кратности 1).


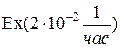 .
.
Найдем показатели надежности 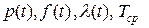 системы.
системы.
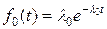 ,
, 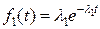
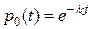 ,
, 
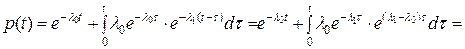
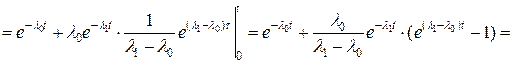

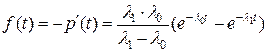
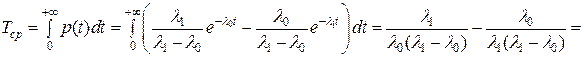
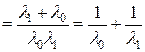 .
.
Таким образом:
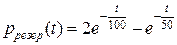 ,
,
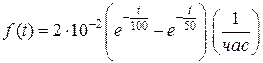 ,
,
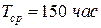 ,
, 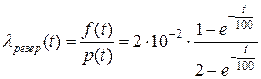 .
.
Найдем еще выигрыши  ,
, 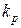 ,
, 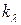 в надежности системы по
в надежности системы по 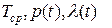 при сравнении ее с нерезервированной системой.
при сравнении ее с нерезервированной системой.
 =
= =
= ;
;
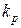 =
=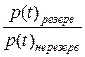 =
= ;
;
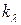 =
= =
=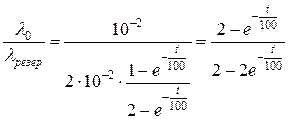 .
.
5.5. Рассмотрим резервированную систему из n элементов одинаковой надежности, для работы которой необходимо, чтобы работало не менее m элементов:

(17)
m
m+1
n
Тогда функцию надежности  системы найдем по формуле полной вероятности:
системы найдем по формуле полной вероятности:

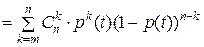 , (18)
, (18)
где p(t) – функция надежности каждого элемента.
Найдем функцию плотности вероятностей распределения времени наработки на отказ:
 , (19)
, (19)
где f(t) – функция плотности вероятностей для каждого элемента.
Действительно:

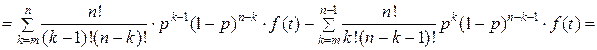


 . (20)
. (20)
Данный тип резервирования используется в цифровых устройствах, когда сигнал в двоичном коде ( логическое 0 или 1) подается на систему вида (17), состоящую из нечетного числа элементов одинаковой надежности.
Для нормальной работы системы необходимо, чтобы сигнал проходил без искажений большинство элементов (закон большинства, или мажоритарный закон). На практике часто рассматривают системы «2 из 3-х», или «3 из 5».
Пример 6. Рассмотрим систему «2 из 3-х»:

2 4
Сигналы на входе и выходе элементов – в двоичном коде. Сигнал на выходе четвертого элемента формируется по мажоритарному принципу из 3 входящих и равен значению большинства. Элементы 1, 2, 3 – равнонадежны:
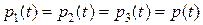 .
.
Для нормальной работы такой системы необходимо и достаточно, чтобы работали без искажений хотя бы 2 из 3 первых элементов и 4-й элемент.
Тогда, используя формулу (18), получим
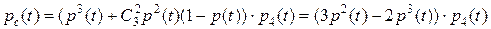 .
.
Предположим, что 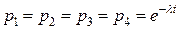 и найдем выигрыш
и найдем выигрыш 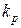 в надежности по вероятности безотказной работы системы при сравнении ее с системой
в надежности по вероятности безотказной работы системы при сравнении ее с системой
 p(t) p(t)
p(t) p(t)
 .
.
Решим неравенство 
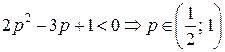 , т.е. при
, т.е. при 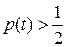 надежность системы, по сравнению с нерезервированной, больше. Найдем интервал времени:
надежность системы, по сравнению с нерезервированной, больше. Найдем интервал времени:
 .
.
Найдем еще  .
.
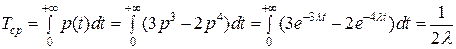 .
.
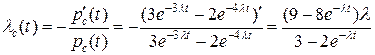 ;
;
 и
и 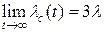 .
.
Упражнения.
5.2. Резервированная невосстанавливаемая система состоит из 2-х параллельно соединенных элементов (постоянно включенный резерв). Время жизни каждого… Ответ:а) , ,Гамма-функция и ее свойства.
Определение 1. Несобственный интеграл , (1) где , называется эйлеровым интегралом 2-ого рода, а функция переменной z называется гамма-функцией Эйлера. При этом…Упражнения
6.1. Вычислить 1) 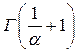 ; 2)
; 2)  , если а)
, если а) 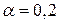 ; б)
; б) 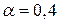 .
.
6.2.Проверить справедливость формулы
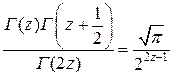 при
при 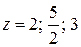 .
.
6.3.Вычислить а)  , б)
, б) 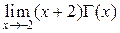 , и)
, и)  .
.
Ответ:а) – 1; б) 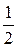 ; в)
; в) 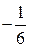 .
.
Некоторые законы распределения времени наработки на отказ.
7.1.Экспоненциальный закон . Подробно рассмотрен в §§ 2, 3. .Упражнения.
Ответ. , . 7.2.Нерезервированная система состоит из n последовательно соединенных… Ответ.1)Ответ. .
7.7.Время Т наработки системы на отказ распределено по закону , при этом интенсивность отказов при t=5000 час равна: . Найти 1) параметр ; 2) ,… 7.8.Нерезервированная система состоит из 2-х последовательно соединенных… 7.9.Время Т наработки элемента на отказ распределено по закону Вейбулла . При этом интенсивность отказов .Гамма - распределение.
Определение 1. Случайная величина Т имеет гамма – распределение , если ее функция распределения , (1) где – неполная гамма – функция (см. §6), – параметры распределения; .Решение.
 .
.
Тогда, по формуле (7)
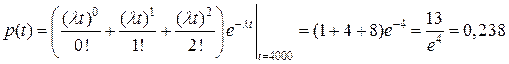 .
.
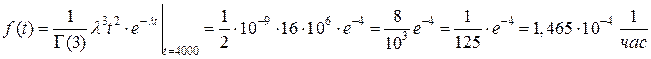 .
.
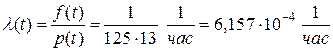 .
.
Упражнения.
1) Записать функции: . 2) Найти Тср , D(T). 3) Найти показатели надежности при час.Приложение 2. РГР Законы распределения времени наработки на отказ.
Постановка задачи
Система состоит из трех последовательно соединенных элементов, законы распределения времени наработки на отказ которых приведены в таблице. Найти показатели надежности каждого элемента и всей системы в целом:
1. Среднее время жизни , среднее квадратическое отклонение 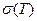 для каждого элемента, где
для каждого элемента, где  - время наработки на отказ.
- время наработки на отказ.
2. Функцию плотности вероятностей для случайной величины  .
.
3. Функцию надежности.
4. Функцию интенсивности отказов.
5. Построить графики  .
.
6. Протабулировать функции 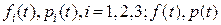 .
.
7. Среднее время жизни системы.
Задания
| В1 | В2 | В3 | В4 | В5 | |
| 1-й элемент | W(2;1/1500) | R(1/1000) | W(1;1/2000) | W(3;1/3000) | W(4;1/2000) |
| 2-й элемент | Г(8;1/200) | Exp(1/1000) | Г(5;1/500) | Г(7;1/1000) | W(1;1/1500) |
| 3-й элемент | TN(1500;800) | TN(3000;300) | TN(1000;700) | TN(1000;800) | TN(100;800) |
| В6 | В7 | В8 | В9 | В10 | |
| 1-й элемент | W(4;1/3000) | R(1/2000) | W(5;1/3000) | Г(5;1/800) | W(6;1/3000) |
| 2-й элемент | Г(6;1/800) | Г(6;1/800) | Г(6;1/1000) | Г(5;1/800) | W(6;1/3000) |
| 3-й элемент | TN(0;1000) | TN(200;800) | R(1/3000) | Exp(1/2000) | TN(500;1000) |
| В11 | В12 | В13 | В14 | В15 | |
| 1-й элемент | W(5;1/2000) | R(1/1500) | W(1/5;1/3) | R(1/1600) | W(4;1/1800) |
| 2-й элемент | TN(600;1000) | Г(7;1/1500) | Г(7;1/200) | R(1/1600) | W(1;1/1400) |
| 3-й элемент | TN(600;1000) | TN(700;1000) | TN(700;1000) | TN(800;1000) | TN(150;800) |
| В16 | В17 | В18 | В19 | В20 | |
| 1-й элемент | W(2;1/1600) | R(1/1200) | W(1;1/2200) | W(3;1/3200) | W(4;1/2300) |
| 2-й элемент | Г(8;1/250) | Exp(1/1200) | Г(5;1/550) | Г(7;1/1200) | W(1;1/1600) |
| 3-й элемент | TN(1400;800) | TN(2500;300) | TN(900;700) | TN(1200;800) | TN(350;800) |
| В21 | В22 | В23 | В24 | В25 | |
| 1-й элемент | W(4;1/3100) | R(1/2200) | W(5;1/3100) | Г(5;1/850) | W(6;1/3200) |
| 2-й элемент | Г(6;1/900) | Г(6;1/900) | Г(6;1/1100) | Г(5;1/850) | W(6;1/3200) |
| 3-й элемент | TN(0;1200) | TN(200;850) | R(1/3100) | Exp(1/2200) | TN(500;1200) |
| В26 | В27 | В28 | В29 | В30 | |
| 1-й элемент | W(5;1/2100) | R(1/1600) | W(1/5;1/3) | R(1/1700) | W(4;1/1900) |
| 2-й элемент | TN(600;1100) | Г(7;1/1600) | Г(7;1/220) | R(1/1700) | W(1;1/1500) |
| 3-й элемент | TN(600;1100) | TN(700;1300) | TN(700;1100) | TN(800;1200) | TN(250;800) |
Пример решения в среде Mathematica.
Текстовая ячейка Subsubtitle
Законы распределения времени наработки на отказ элементов:

|
| Текстовая ячейка Subtitle Показатели надежности для W(aa,ll) |
Группа ячеек ввода
aa:= 2
ll:=1/2000
MT:=Gamma[1+1/aa]/ll
sT:=Sqrt[(Gamma[1+2/aa]-(Gamma[1+1/aa])^2)]/ll
Labeled[N[MT],Среднее время жизни,Left]
Labeled[N[sT],Среднее квадратическое отклонение, Left]
f1= aa*(ll^aa)*(x^(aa-1))*Exp[-((ll*x)^aa)]
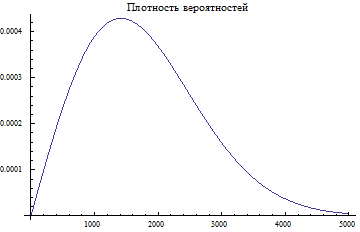
p1=Exp[-((ll*x)^aa)]
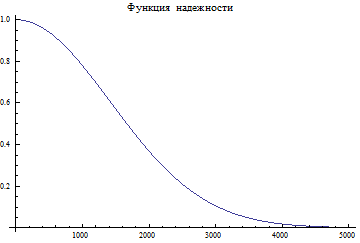
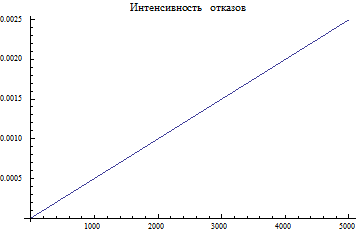
lam1=aa*(ll^aa)*(x^(aa-1))
Plot[f1,{x,0,5000}, PlotLabel "Плотность вероятностей"]
Plot[p1,{x,0,5000},PlotLabel "Функция надежности "]
Plot[lam1,{x,0,5000}, PlotLabel "Интенсивность отказов"]
------Ячейки вывода ---------------------------
Время жизни Среднее 1772.45
Среднее отклонение квадратическое 926.503
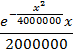
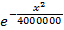

|
| Текстовая ячейка Subtitle Показатели надежности для Г(a,l) |
Группа ячеек ввода
l:=1/300
a:=5
Labeled[a/l, Среднее время жизни,Left]
Labeled[N[Sqrt[a]/l], Среднее квадратическое отклонение, Left]
f2=(l^a)*(x^(a-1))*Exp[-l*x]/Gamma[a]
p2=Gamma[a,l*x]/Gamma[a]
lam2=((l^a)*(x^(a-1))*Exp[-l*x])/(Gamma[a,l*x])
Plot[f2,{x,0,5000}, PlotLabel "Плотность вероятностей"]
Plot[p2,{x,0,5000},PlotLabel "Функция надежности "]
Plot[lam2,{x,0,5000}, PlotLabel "Интенсивность отказов"]
------Ячейки вывода ---------------------------
Время жизни Среднее 1500
Среднее отклонение квадратическое 670.82
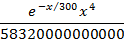
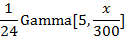




|
Текстовая ячейка Subtitle
Показатели надежности для TN(aaa,s), функция Лапласа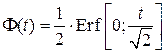 . .
|
Группа ячеек ввода
aaa:= 2000
s:= 1000
xx:=aaa/s
c=1/(0.5+0.5*Erf[0,xx/Sqrt[2]])
k=(c/Sqrt[2*Pi])*Exp[-(xx^2)/2]
Labeled[N[aaa+k*s], Среднее время жизни ,Left]
Labeled[N[s*Sqrt[1+k*xx-k^2]], Среднее квадратическое отклонение , Left]
f3=c*PDF[NormalDistribution[aaa,s],x]
p3=c*(0.5-0.5*Erf[0,(x-aaa)/(s*Sqrt[2])])
lam3=c*PDF[NormalDistribution[aaa,s],x]/p3
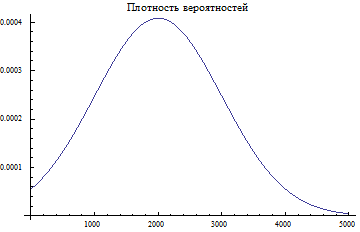
Plot[f3,{x,0,5000}, PlotLabel "Плотность вероятностей"]
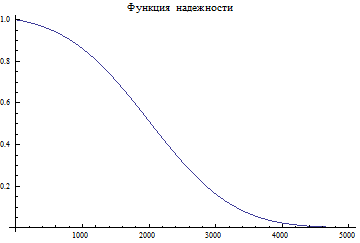
Plot[p3,{x,0,5000},PlotLabel "Функция надежности "]
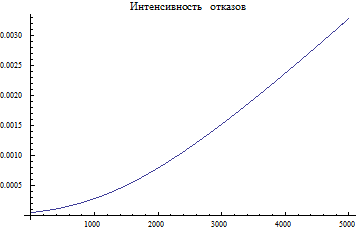
Plot[lam3,{x,0,5000}, PlotLabel "Интенсивность отказов"]
------Ячейки вывода ---------------------------
1.02328
0.0552479
Время жизни Среднее 2055.25
Среднее отклонение квадратическое 1052.35

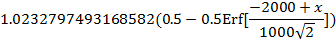
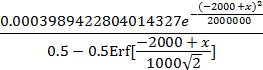
|
| Текстовая ячейка Subtitle Функция надежности системы |
Группа ячеек ввода
p= p1*p2*p3
Plot[p,{x,0,5000},PlotLabel® "Функция надежности системы "]
------Ячейки вывода ---------------------------
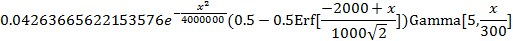
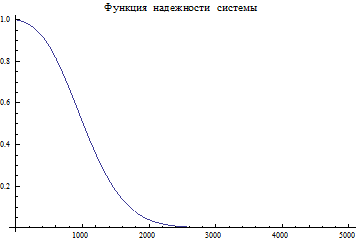
|
| Текстовая ячейка Subtitle Интенсивность отказа системы |
Группа ячеек ввода
lam=lam1+lam2+lam3
Plot[lam,{x,0,5000}, PlotLabel® " Интенсивность отказов системы"]
------Ячейки вывода ---------------------------
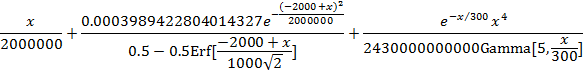
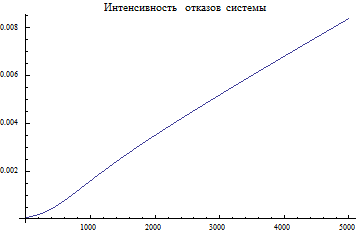
|
| Текстовая ячейка Subtitle Плотность распределения вероятностей системы |
Группа ячеек ввода
f:= p*lam
Plot[f,{x,0,5000}, PlotLabel "Плотность распределения времени наработки на отказ системы"]
------Ячейки вывода ---------------------------

|
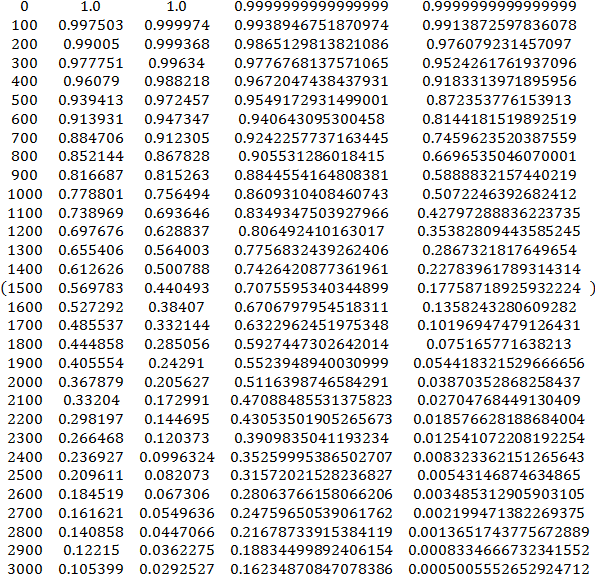
| Текстовая ячейка Subtitle Таблица значений функций p(i), i=1,…,3 и p с шагом 100 час |
Группа ячеек ввода
MatrixForm[Table[{x,N[p1,6],N[p2,6],N[p3,6],N[p,6]},{x,0,3000,100}]]
------Ячейки вывода ---------------------------
|
| Текстовая ячейка Subtitle Таблица значений функций f(i), i=1,…,3 и f с шагом 100 час |
Группа ячеек ввода
MatrixForm[Table[{x,N[f1,6],N[f2,6],N[f3,6],N[f,6]},{x,0,
3000,100}]]
------Ячейки вывода ---------------------------

|
| Текстовая ячейка Subtitle Среднее время жизни системы |
Группа ячеек ввода
 ------Ячейки вывода ---------------------------
------Ячейки вывода ---------------------------
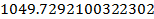
|
ЛИТЕРАТУРА
1. А.М. Половко, С.В. Гуров. Основы теории надежности. С. – Петербург, БХВ – Петербург, 2008.
2. А.М. Половко, С.В. Гуров. Основы теории надежности. Практикум. С. – Петербург, БХВ – Петербург, 2006.
3. В.К. Саульев. Математическая теория надежности и восстановления. – Москва, МАИ, 1974.
4. Н.П. Ямпурин, А.В. Баранова. Основы надежности электронных средств. – Москва, Изд. центр «Академия», 2010.
5. Т.А.Голинкевич. Прикладная теория надежности. – М. Высшая школа, 1977.
6. Г.Н. Черкасов. Надежность аппаратно-программных комплексов. Учебное пособие. – СП.б.: Питер, 2005.
7. А.М. Половко. Mathematica для студента. – СП.б.: БХВ – Петербург, 2007.
СОДЕРЖАНИЕ
§ 1. Вероятностное пространство. 3
Упражнения. 6
§ 2. Случайные величины. 8
§ 3. Основные понятия теории надежности. 14
§ 4. Статистическое оценивание показателей надежности. 20
§ 5. Показатели надежности для сложных систем. 24
§ 6. Гамма-функция и ее свойства. 36
§ 7. Некоторые законы распределения времени наработки на отказ. 37
§ 8. Усеченное нормальное распределение. 46
§ 9. Логарифмическое нормальное распределение. 49
§ 10. Гамма - распределение. 51
§ 11. Распределение 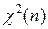 . 56
. 56
§ 12. Случайные процессы. 60
§ 13. Цепи Маркова. 62
§ 14. Потоки событий. 71
§ 15. Марковcкие процессы с дискретными состояниями и непрерывным временем. 73
Приложение 1. Вычисления в среде Mathematica. 89
Приложение 2. РГР Законы распределения времени наработки на отказ. 95
ЛИТЕРАТУРА.. 106
Учебное издание
ЗАДАНИЯ И МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ДЛЯ ТИПОВЫХ РАСЧЕТОВ
ПО МАТЕМАТИКЕ
для студентов 1 курса
энергетического факультета
Составители:
РУДЫЙ Александр Никодимович
Редактор Т.Н. Микулик
_____________________________________________________________
Подписано в печать .2009.
Формат 60×84 . Бумага офсетная.
. Бумага офсетная.
Отпечатано на ризографе. Гарнитура Таймс.
Усл. печ. л. 5,81. Уч.-изд. л. 2,27. Тираж . Заказ .
____________________________________________________________
Издатель и полиграфическое исполнение:
Белорусский национальный технический университет.
ЛИ № 02330/0131627 от 01.04.2004.
Проспект Независимости, 65, 220013, Минск.
– Конец работы –
Используемые теги: Теория, вероятностей, задачах0.069
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: ТЕОРИЯ ВЕРОЯТНОСТЕЙ В ЗАДАЧАХ
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов